空間分層數(shù)據(jù)無條件模型的改進及其估計

閔素芹,何曉群

(1.中國傳媒大學理學院,北京100024;2.西京學院應用統(tǒng)計科學研究中心,西安710123)

空間分層數(shù)據(jù)無條件模型的改進及其估計

閔素芹1,何曉群2

(1.中國傳媒大學理學院,北京100024;2.西京學院應用統(tǒng)計科學研究中心,西安710123)

抽樣調(diào)查中得到的數(shù)據(jù)經(jīng)常既包含個體信息又包含地理單元信息,形成以地區(qū)集聚的分層數(shù)據(jù)。空間分層數(shù)據(jù)中地理單元間往往具有空間依賴性,區(qū)別于傳統(tǒng)的分層數(shù)據(jù)。分析空間分層數(shù)據(jù)時需要首先建立無條件模型用作初步分析。因此,在傳統(tǒng)分層無條件模型中引入完全空間自回歸模型來表達空間相關性,建立空間分層數(shù)據(jù)的無條件模型,并研究其估計方法,借助參數(shù)估計值可做模型選擇。

無條件模型;空間依賴性;分層數(shù)據(jù);EM算法

0 引言

社會科學研究中,樣本往往來自不同的層次和單位,很多研究中采取的抽樣方式為分層隨機抽樣,在這樣的抽樣設計下,個體的特征會產(chǎn)生集聚現(xiàn)象,由此得到的數(shù)據(jù)帶來了分層的結構。比如,在抽樣調(diào)查中,數(shù)據(jù)往往既包含個人信息,又有關于所在地區(qū)的信息。可以把這樣的數(shù)據(jù)結構分層,個人信息看作第一層,地區(qū)作為第二層,即個人嵌套于地區(qū)。分層線性模型適用于處理此類數(shù)據(jù),隨著計算機技術水平的飛速發(fā)展,其估計方法的計算問題得以解決,近年來在社會科學和行為科學領域應用越來越廣泛。

分層數(shù)據(jù)分析中經(jīng)常將無條件模型用作初步分析,它可以提供兩個層次中結果的變化信息。如Frenzel等(2007)[1]、Espelage等(2011)[2]、Simms(2014)[3]的研究中都首先運用無條件模型計算組內(nèi)方差、組間方差、及組內(nèi)相關系數(shù)(ICC),得出造成因變量的組間變異是不可忽略的,從而有必要進一步建立一般分層模型。Neupert等(2015)基于對51名60～96歲的老年人380天每天一次的追蹤調(diào)查數(shù)據(jù),運用分層模型研究應激預應對如何影響老年人的身體健康、記憶力減退等問題。重復測量的個體變化數(shù)據(jù)即縱向數(shù)據(jù),將每一個人的多次測量視為嵌套于這個人。在利用分層線性模型時,層-1為重復觀察模型,層-2為關注個體間差異的個人層次模型。研究中運用無條件模型分析了每天的應激預應對觀測數(shù)據(jù)存在顯著的個體內(nèi)方差,結果表明每個人的應激預應對是動態(tài)變化的[4]。

在抽樣調(diào)查中采用分層抽樣設計時,層的劃分常常按照行政區(qū)劃進行,這樣得到的數(shù)據(jù)既包含個體信息,又包含關于區(qū)域、城鎮(zhèn)、市、省等的地理單元信息,就形成了以地區(qū)集聚的分層數(shù)據(jù)。空間分層數(shù)據(jù)因為地理單元間往往具有空間自相關性,區(qū)別于傳統(tǒng)的分層數(shù)據(jù)。Ancelin也提到空間統(tǒng)計所面臨的挑戰(zhàn)時指出按一層觀測值(如:空間單元層)進行的分析,不能提供低層(如個體行為)有用的信息[5]。由于傳統(tǒng)分層模型假定地區(qū)間(組間)相互獨立,而地理單元之間的空間相關性使得層-2模型殘差的假設分布不再成立,從而估計出現(xiàn)問題。在分析空間分層數(shù)據(jù)時,也需要首先建立無條件模型。本文在分層模型中引入完全空間自回歸模型來表達空間相關性,改進了傳統(tǒng)分層數(shù)據(jù)的無條件模型,并研究其估計方法,依據(jù)參數(shù)估計值選擇是否需要采用考慮空間效應的分層模型。

1 空間分層數(shù)據(jù)無條件模型的構建

無條件模型是最簡單的分層線性模型,這種情況下層-1和層-2模型都不含自變量,模型為:

γ00代表總體中結果的總平均數(shù),ξ0j為第j個組的隨機效應,假定其均值為0,方差為τ00,σ2代表組內(nèi)變化, τ00則捕獲了組間變化。

對于空間分層數(shù)據(jù),層-2模型殘差分布的假設不再成立,殘差的空間模式存在空間依賴性,引入能夠描述空間自相關的項能有效的克服模型的缺陷。

在分析空間分層數(shù)據(jù)時,空間自相關反映為鄰近地區(qū)β0間的依賴性,即地區(qū)1的β01,地區(qū)2的β02,…,地區(qū)J的β0J存在空間自相關。本文考慮在層-2模型中引入空間效應,空間效應用完全空間自回歸模型來表達。此時,層-1模型與傳統(tǒng)分層模型(1)一致,其中,yij是因變量, β0j是截距項,εij是隨機誤差項。

若以矩陣向量的方式表達,則式(1)為:

而空間分層數(shù)據(jù)中β0具有空間效應,此時,層-2模型為:

此模型為完全空間自相關模型,不包含解釋變量。其中,ρ表示空間自相關系數(shù),W表示J×J的空間權重矩陣,通常是二元對稱矩陣,表達J個地理單元的空間鄰近關系。

綜上,帶空間效應的兩層模型的無條件模型表達為:

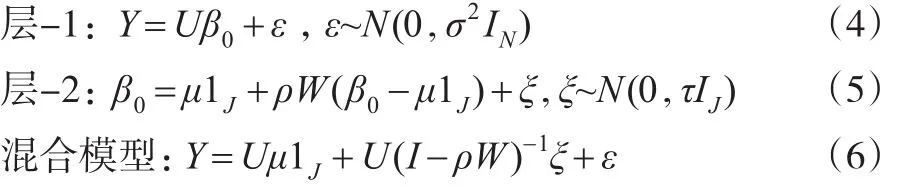
模型中,ρ＞0表示該地區(qū)被結果變量的值與其相似的地區(qū)所包圍,即:結果變量高值的地區(qū)被其他相似的高值地區(qū)所包圍,低值被低值所包圍。另一方面,ρ＜0表示高值的地區(qū)被低值地區(qū)所包圍。ρ=0則表示沒有空間依賴,此時模型為普通的帶隨機效應的單因素方差分析模型。

2 無條件空間分層模型的最大似然估計

空間分層數(shù)據(jù)的無條件模型層-1無自變量,層-2為完全自回歸模型。與傳統(tǒng)兩層模型相比,增加了空間效應表示部分,其中空間權重矩陣W是已知的,多了一個需要估計的參數(shù)ρ。要通過最大似然估計方法估計模型中的參數(shù)ρ，σ2，μ，τ。

下面給出期望最大化(EM)算法。期望最大化算法認為y是觀測數(shù)據(jù),ξ是缺失數(shù)據(jù)。因此,完整數(shù)據(jù)為(y，ξ),ρ，σ2，μ，τ是需要被估計的參數(shù)。

2.1 最大化步(M Step)

ξ是未知的層-2模型的誤差項向量,其假設為:

因此,給定β0，σ2后y的條件分布為:

因E[y|ρ，σ2，μ，τ]=Uμ1J,V[y|ρ，σ2，μ，τ]=τU(I-ρW)-1(I-ρW)-1TUT+σ2IN,故,當ρ，σ2，μ，τ也為已知的情況下,y的條件分布為:

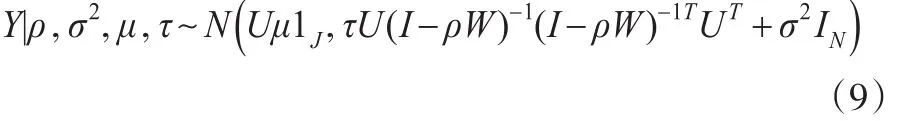
而且,cov(y，ξ)|ρ，σ2，μ，τ=cov(Uμ1J+U(I-ρW)-1ξ+ε，ξ)=E[(Uμ1J+U(I-ρW)-1ξ+ε-Uμ1J)ξT]=τU(I-ρW)-1

所以,y與ξ的聯(lián)合分布為:

完整數(shù)據(jù)的似然函數(shù)取自然對數(shù),得:

而,ln f(y，ξ|ρ，σ2，μ，τ)=ln l(ρ，σ2，μ，τ|y，ξ)對數(shù)似然函數(shù)ln l(ρ，σ2，μ，τ|y，ξ)分別對ρ，σ2，μ，τ偏微分,

但是,無法給出ρ的顯式表達。所以,考慮結合運用Fisher得分算法。得分向量為:

各分量由式(13)至式(15)給出。

Hessian矩陣為:

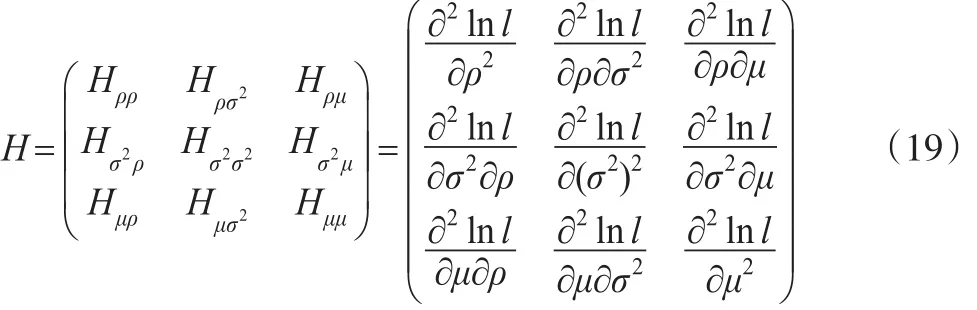
Fisher得分方法需要求二階導數(shù)的期望矩陣,

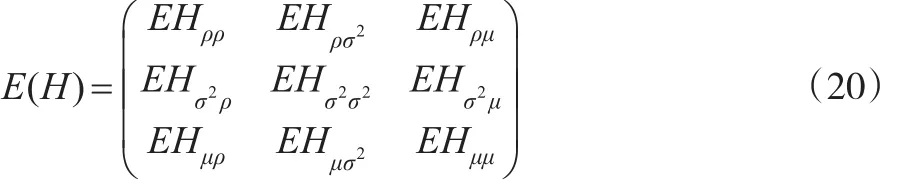
2.2 期望步

由式(10),根據(jù)正態(tài)分布剖分定理,y為已知的條件下ξ的條件分布的條件期望向量和條件方差協(xié)方差矩陣分別為:

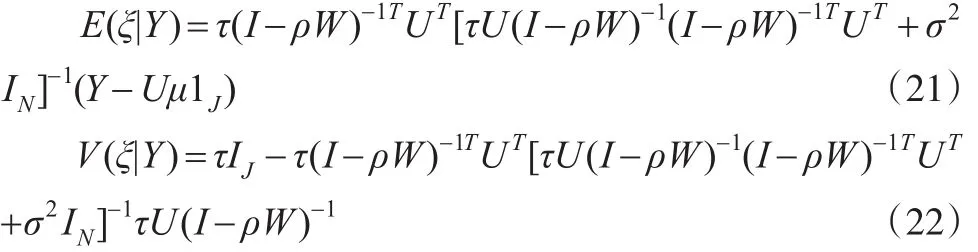
將式(21)記為a,式(22)記為B。故,若y與ρ，σ2，μ，τ已知,由式(21)、(22),ξ的事后條件分布為:

2.3 EM算法

(1)給出初始值ρ(0)，(σ2)(0)，μ(0)，τ(0);記ρ(k)，(σ2)(k)，μ(k)，τ(k)是第k+1次迭代開始時參數(shù)的估計值;

(2)估計完整數(shù)據(jù)的充分統(tǒng)計量:E(ξ|y，ρ，σ2，μ，τ)，E(ξTξ|y，ρ，σ2，μ，τ)

式(24)與式(25),這些期望值根據(jù)前一步迭代得到的ρ(k)，(σ2)(k)，μ(k)，τ(k)值求得;

(4)將新的參數(shù)估計值代入到步驟(2)中,重復上述步驟,M步和E步不斷地迭代交互運算,直到所估計的參數(shù)值都很接近,或每次迭代運算的對數(shù)似然函數(shù)值變化很小,就達到收斂。可以通過計算每一步迭代的對數(shù)似然值來加以監(jiān)測。

3 結論

根據(jù)參數(shù)ρ的值與其顯著性可以反映鄰近地區(qū)β0間的依賴性,根據(jù)σ2，τ的估計值,計算組內(nèi)相關系數(shù)如果空間自回歸系數(shù)ρ顯著不為零,則認為空間自相關需要考慮,ICC≥0.059表示組間差異不可忽略[6]。此時,需要進一步建立空間分層模型進行后續(xù)分析。若ρ=0,ICC≥0.059則表示沒有空間依賴性,但組間變異不可忽略,此時應選用傳統(tǒng)分層線性模型進行后續(xù)分析。

[1]Frenzel A C,Pekrun R,Goetz T.Perceived Learning Environment and Students'Emotional Experiences:AMultilevel Analysis ofMathematics Classrooms[J].Learningand Instruction,2007,17(5).

[2]Espelage D,Green H,Polanin J,w illingness to Intervene in Bullying Episodes Among Middle School Students Individual and Peer一group Influences[J].The Journalof Early Adolescence,2011,(11).

[3]Simms K.Are Expectations About Health Care Universal?The International Evidence[J].Global Journal of Business and Social Science, 2014,1(10).

[4]NeupertSD,EnnisG E,Ramsey JL,etal.Solving Tomorrow's Problems Today?Daily Anticipatory Copingand Reactivity to Daily Stressors[J].The Journals of Gerontology Series B:Psychological Sciences and Social Sciences,2015,(3).

[5]Anselin L.The Future of Spatial Analysis in The Social Sciences[J]. Geographic Information Sciences,1999,5(2).

[6]溫福星.階層線性模型的原理與應用[M].北京:中國輕工業(yè)出版社,2009.

(責任編輯/亦民)

O212

A

1002-6487(2016)20-0016-03

北京高等學校“青年英才計劃”項目(y ETP0611);中國傳媒大學優(yōu)秀中青年教師培養(yǎng)工程(y XJS2013330);中國傳媒大學理工科規(guī)劃項目(XNL1402)

閔素芹(1978—),女,山東青州人,博士,副教授,研究方向:統(tǒng)計模型理論與應用。何曉群(1954—),男,陜西西安人,教授,博士生導師,研究方向:應用數(shù)理統(tǒng)計。