基于非負矩陣分解的單通道故障特征分離方法

梁 霖， 栗茂林， 李利邦， 劉 飛， 徐光華,3

(1.西安交通大學機械工程學院 西安，710049) (2.西安交通大學工程坊 西安，710049) (3.西安交通大學機械制造系統工程國家重點實驗室 西安，710054)

?

基于非負矩陣分解的單通道故障特征分離方法

梁 霖1， 栗茂林2， 李利邦1， 劉 飛1， 徐光華1,3

(1.西安交通大學機械工程學院 西安，710049) (2.西安交通大學工程坊 西安，710049) (3.西安交通大學機械制造系統工程國家重點實驗室 西安，710054)

針對單通道振動信號的多特征分離問題，提出了一種基于正交非負矩陣分解的故障特征提取方法。首先，采用短時傅里葉變換，利用時頻分布來描述信號中的局部故障特征，通過核心一致性指標評估子空間維數；然后，在幅值譜矩陣分解的基礎上，通過正交性約束實現低維嵌入分量信息的分離，獲取局部特征的準確描述；最后，采用相位恢復理論重構出特征波形，對仿真信號和滾動軸承故障數據進行了測試。結果表明，所提出的方法能利用單通道信號有效地分離出微弱的局部故障特征，為機械狀態的早期故障診斷識別提供了一種有效手段。

非負矩陣分解； 單通道信號； 特征提取； 故障診斷

引 言

在設備運行狀態的監測診斷中，軸承座上的測量傳感器能夠提供多個部件的信息，包括齒輪振動及嚙合、軸承振動，轉子振動以及其他干擾噪聲等。在某些情況下，振動信息只能利用單傳感器采集，考慮到安裝成本，往往在每級單側安裝振動傳感器。因此，需要利用單通道振動信號的盲分離提取出故障特征分量。

對于包含了多源信息的信號來說，通常可以采用變換域濾波方法實現多源分量的分離。比如：采用自適應Winner濾波器實現多信號的分離[1-2]；采用獨立主分量分析、盲源分離、基函數法、稀疏分解以及多參數聯合估計等方法實現多源信號分解[3-6]。非負矩陣分解(non-negative matrix factorization， 簡稱NMF)作為一種新的矩陣分解算法，克服了傳統矩陣分解的很多問題[7-8]，通過對非負矩陣的聚類分析，有效地提取出局部特征[9-13]，同時具有物理意義明確和計算簡單等優勢，成為單通道振動信號源分離的一種有效手段。

由于設備結構、運行環境等因素，往往導致振動測量信號信噪比較低，多振動分量信息相互干擾，通過NMF的局部學習能力，可以有效地將故障振動分量實現分離，從而為運行狀態分析提供解決工具。為此，在單通道信號的NMF特征提取中，通過原始觀測矩陣的構建和低維嵌入維數的選擇，設計基于正交非負矩陣分解的特征分離方法，并通過模擬數據及軸承故障數據進行有效性驗證。

1 非負矩陣分解原理

對一個m維的隨機向量v進行n次觀測，得到觀測矩陣V=[v1,v2,…，vn]，非負矩陣分解的問題可定義為：已知非負矩陣V，找出非負矩陣W和H，使式(1)成立[14]

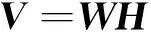
(1)

其中：V為m×n維的非負矩陣；W為m×k維的基矩陣；H為k×n維系數矩陣。

由于m>>k，從而實現了觀測矩陣的約簡。

為了尋找合理的W和H，以常用歐幾里得距離(Euclidean distance)作為目標函數，則式(1)的逼近可以視為一個優化問題

(2)

其中：‖·‖F為矩陣的Frobenius范數。

針對式(2)的優化問題，目前已經提出了多種迭代算法，如乘性迭代算法、梯度下降算法、交替非負最小二乘算法以及改進算法等[15]。

2 正交非負矩陣分解算法

NMF作為一種基于局部表示整體的策略，在提取過程中，若不同源信號間的相似度越低，所表現出的局部性就越強，分解結果就越好。這一特性表現為基向量之間的正交性。在設備故障診斷中，如數據中源信號彼此間的特征差異不明顯，那么分解的向量間就會存在冗余，不利于后續分析。帶有正交性約束的非負矩陣分解方法(orthogonal NMF，簡稱ONMF)[16]可以有效地滿足這種需求，即通過求解正交約束項的優化，獲取的結果帶有正交性。針對基矩陣W和權矩陣H施加正交性的目標式可表示為

(3)

(4)

其中：I為單位矩陣。

式(3)和式(4)可以通過引入拉格朗日乘子求得約束問題的近似解。求解的運算量和矩陣維數密切相關，維數較大，計算量就會很大。因此，將正交性因子矩陣的產生包含在目標優化中[17]，即對W和H施加正交性的目標

(5)

(6)

其中：λ為正交性系數且λ≥0。

求解式(5)的迭代為

(7)

(8)

其中：?表示矩陣元素之間的乘法(除法是矩陣元素之間的除法)。

互換W和H位置可以得到H的正交性懲罰迭代規則

(9)

(10)

由于正交性約束項是嵌入在目標優化方程中，因此最終的正交性是通過分解逐步得到的，無需額外的約束項，其計算量也有顯著下降。

3 基于ONMF的單通道特征分離

結合ONMF和設備振動信號特點，提出了一種基于單通道機械混合振動信號分離方法，通過構造觀測矩陣和選擇子空間維數，基于ONMF的特征分離以及波形重構實現特征分離。

3.1 觀測矩陣的構造

設備故障往往導致振動信號的非平穩性表現，因此，時頻域分析可以有效地提取局部故障信息并構成特征矩陣。目前，時頻分析方法有短時傅里葉變換(short-time Fourier transform，簡稱STFT)、小波變換和小波包分析等。雖然小波與小波包分解方法極大地改善了信號的時頻分析效果，甚至已經逐步成為時頻分析的首選方法。但基函數的選取需要和信號中特征類型相匹配，才能較好地提取信號中的局部特征，而設備振動信號中往往包含多源信號，單一基函數勢必造成局部故障信息衡量的偏差。

相比而言，STFT參數較少、計算簡便，且對振動信號中的高頻突發分量和長周期準平穩分量非常敏感，因此選取STFT進行分析

(11)

其中：x(t)為時域信號；w(t)為窗函數。

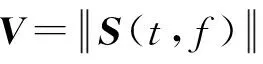
3.2 低維空間維數的選擇

對于高維觀測矩陣來說，低維子空間維數k是分解中的重要參數，直接影響到分解與提取的效果。k值過大會損失降維效果，削弱源信號的信息量，k值較小會降低分解精度，增大冗余。為了克服傳統主分量分析(principal component analysis,簡稱PCA)方法中存在的缺陷，采用核心一致性計算方法來選擇k值[18]，即通過計算數據的平滑系數

(12)

最優分量k的選擇應滿足如下標準

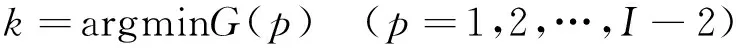
(13)

當G指標最小時，所對應的p值即為由該信號獲取到的觀測矩陣V的最優分解維數k。

3.3 基于ONMF的單通道信號特征提取方法

基于上述分析，對于包含多特征分量振動信號x(t)，提出了一種單通道信號特征提取方法，其流程如下：

1) 將單通道信號通過STFT變換到時頻域中，并保留幅度信息，獲得幅值譜V；

2) 利用核心一致性方法估計出V中的低維子空間維數k值；

3) 基于ONMF算法對V進行k維分解，得到基矩陣W和權矩陣H；

4) 在低維子空間中，選擇目標信號向量對應的幅值譜Ys=W(:,s)*H(s,:)；

5) 根據式(14)所示的相位恢復理論方法重構時頻譜，并基于短時傅里葉變換的逆變換(inverse short-time Fourier transformation，簡稱ISTFT)將時頻譜變換到時域中，獲得分離的特征分量波形xs(t)。

(14)

其中：F為混合信號的時頻譜；Yi為分離出的第i個幅值譜；Si為重構得到的第i個時頻譜(含相位信息)。

4 仿真分析

為了驗證文中特征分離的效果，采用由3個正弦信號構成的仿真信號進行分析。仿真信號表示為

A2sin(2πf2t)+sin(2πf3t)

令：A1=2，A2=2.5，f1=200 Hz，f2=300 Hz，f3=400 Hz。同時將3個正弦信號中的部分波形置零，設采樣頻率為1 000 Hz，采樣點數為1 000點。圖1和圖2分別為3個源信號與混合后的仿真信號波形。

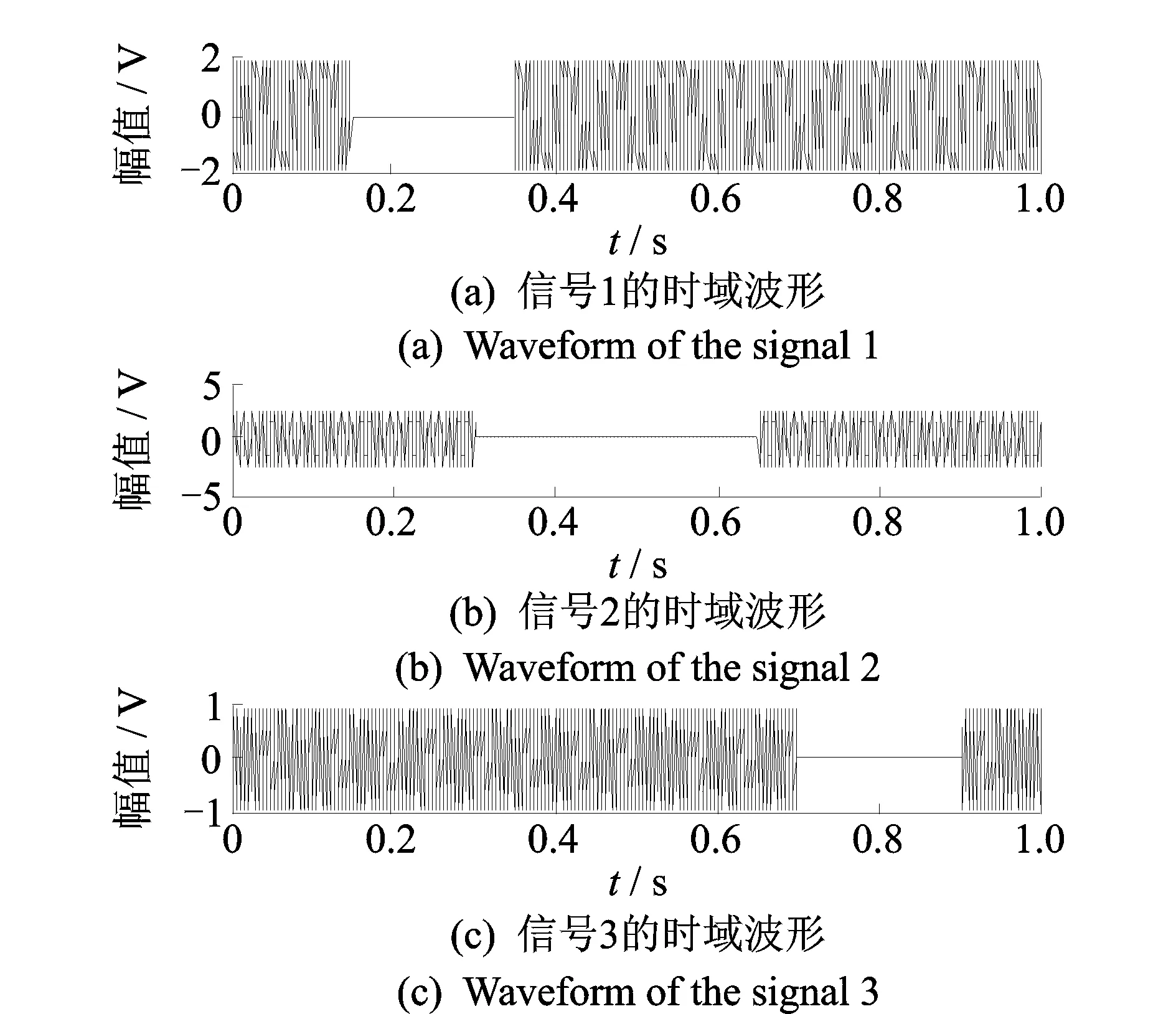
圖1 3個源信號的時域波形Fig.1 Waveform of three simulation signals

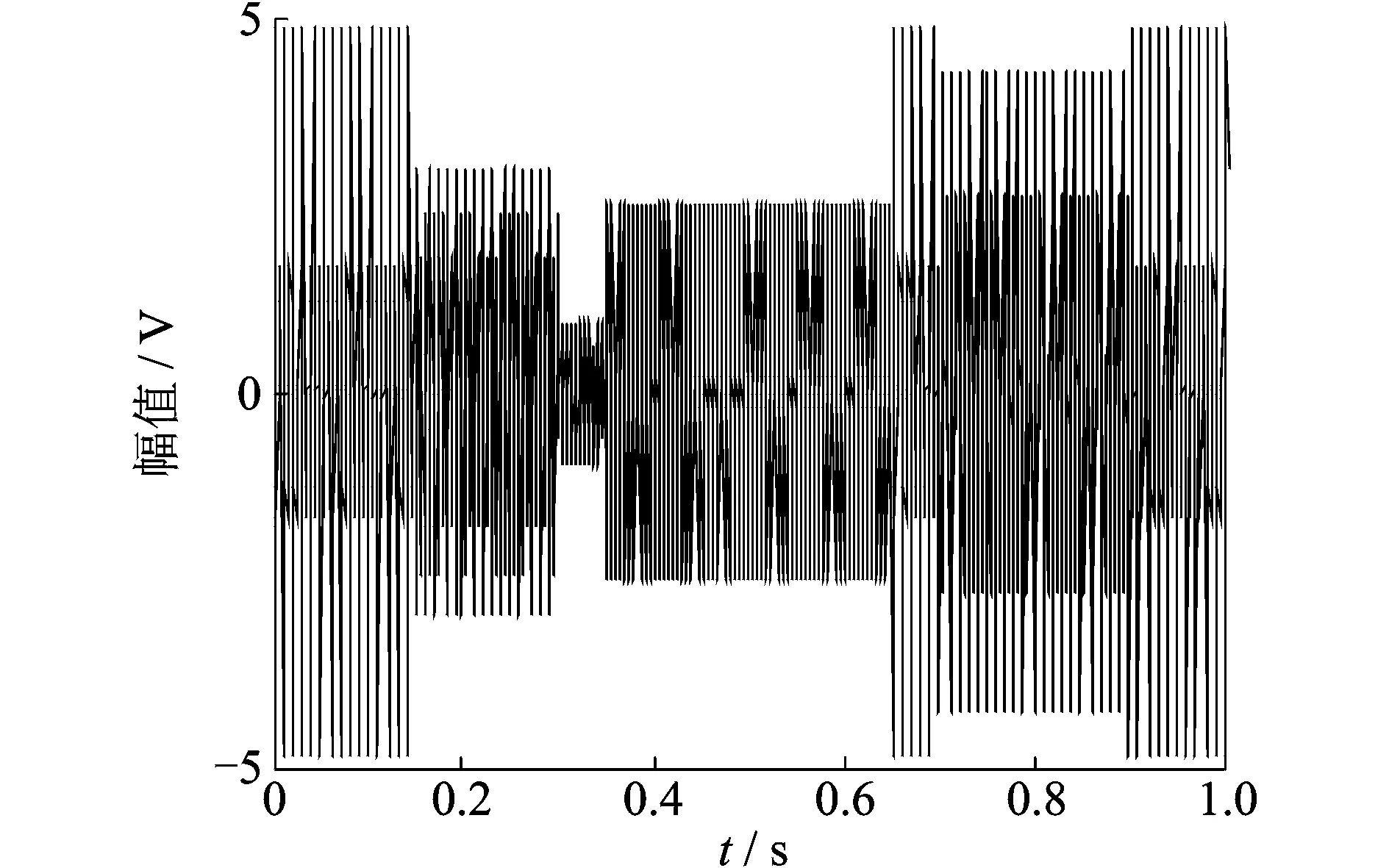
圖2 混合信號的時域波形Fig.2 Waveform of mixed-signal by three simulation signals

對于混合仿真信號，采用文中的特征提取方法進行分析，首先通過STFT獲得時頻譜矩陣，其中窗函數為漢寧窗。在時頻矩陣分解中，采用ONMF提取基函數W與權分布H，其中獲取的W各向量分布如圖3所示。作為對比，采用傳統NMF分解的基矩陣W各向量分布如圖4所示。

對比圖3和圖4的兩種基向量分布可知，由于ONMF加強了基向量間的獨立性，圖3所示的3個基向量間互不干擾地分離出源信號。圖4中由于缺少約束導致傳統NMF分解的基向量間存在冗余，無法準確描述3個正弦信號。其次，結合原信號時頻譜與所提取的沖擊幅度譜，采用ISTFT方法可以獲得圖5所示的時域重構波形。

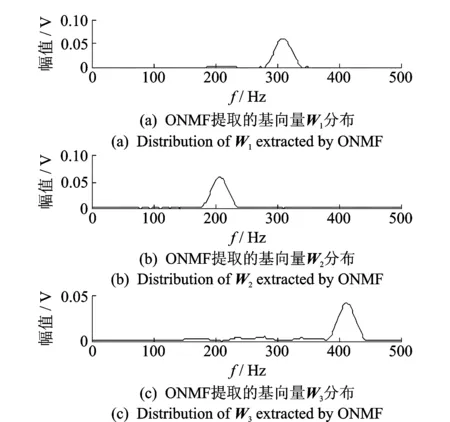
圖3 ONMF提取的基向量W分布Fig.3 Distribution of basis vectors W extracted by ONMF

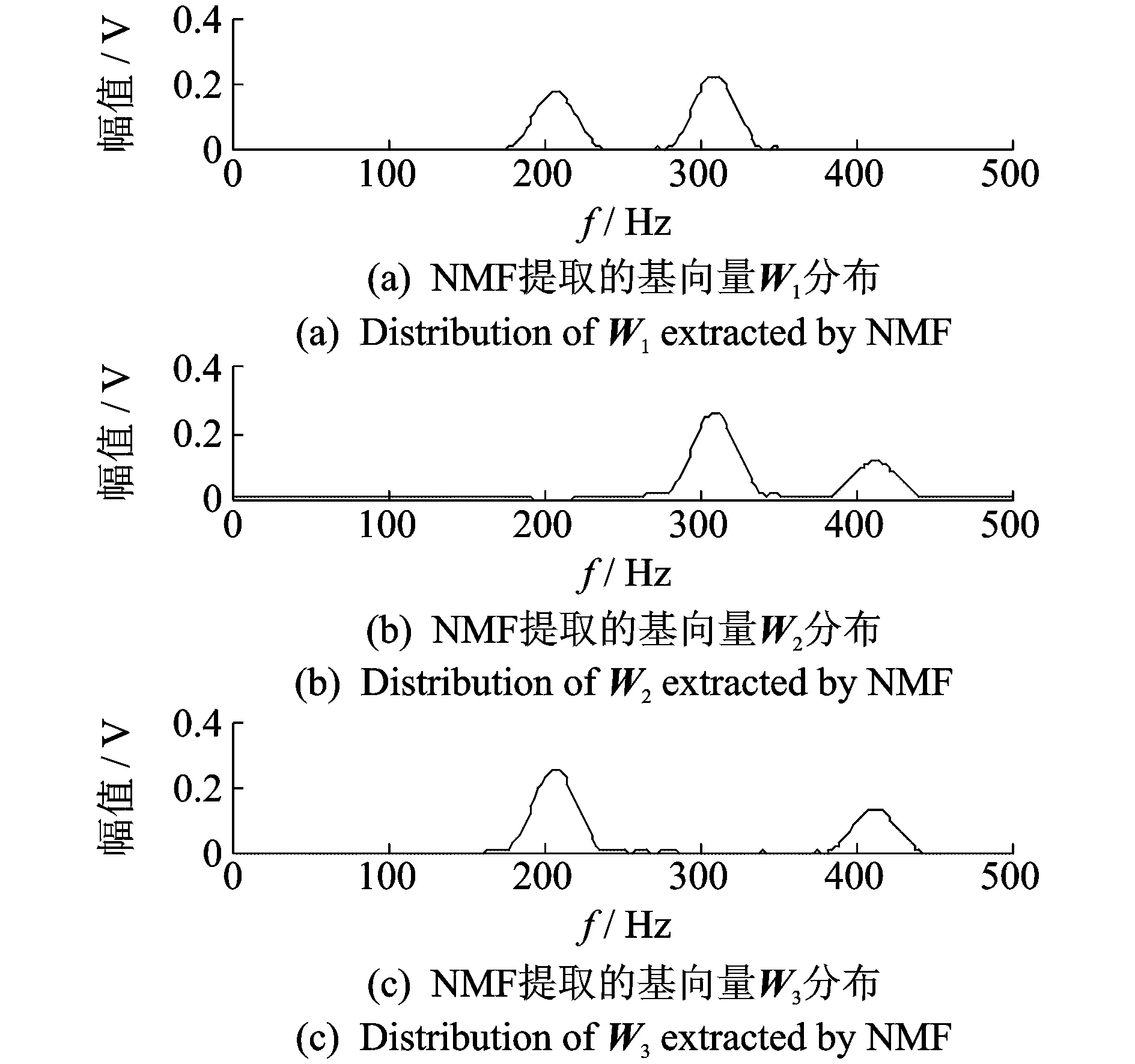
圖4 NMF提取的基向量W分布Fig.4 Distribution of basis vectors W extracted by NMF

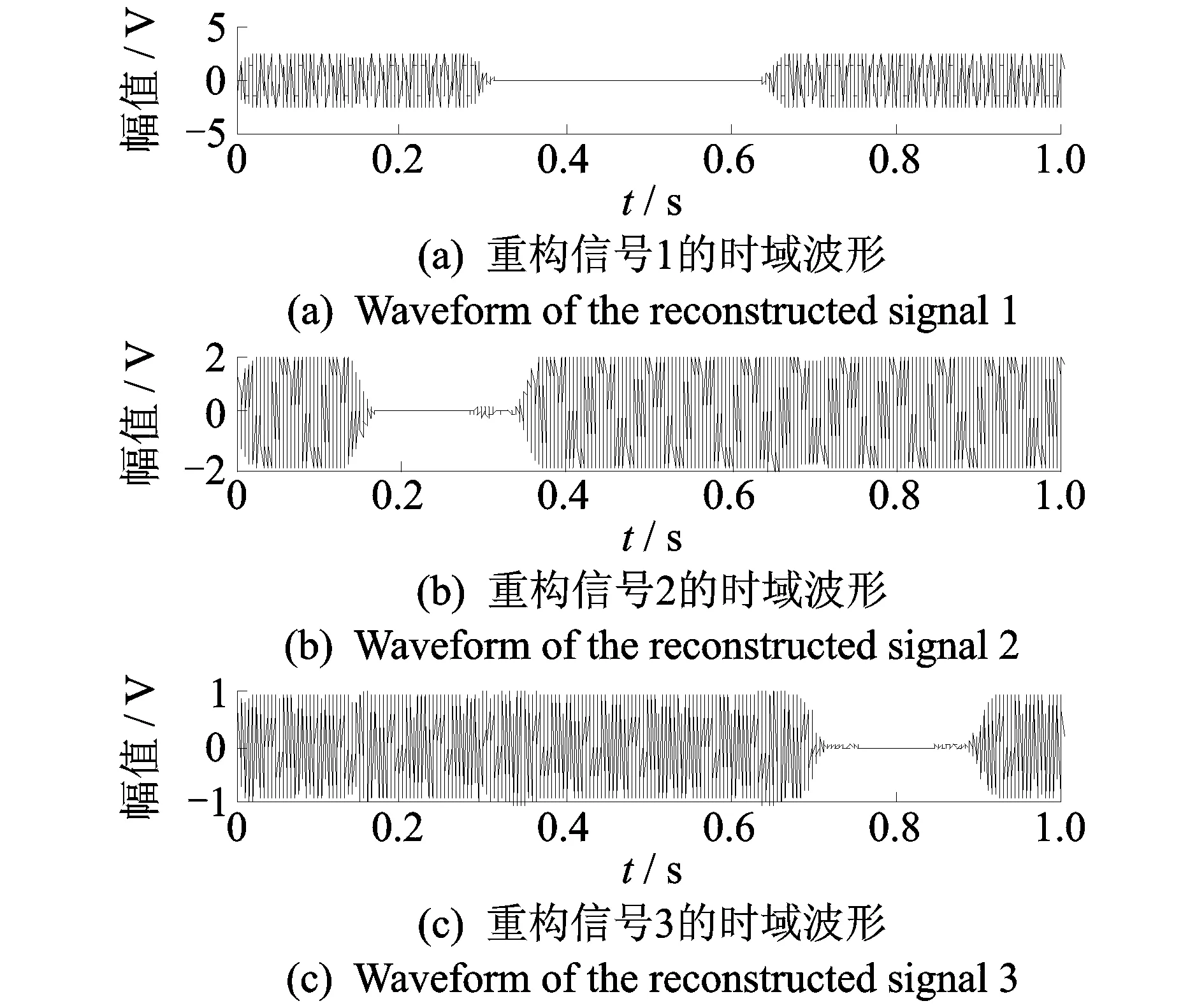
圖5 重構的模擬信號波形Fig.5 Waveform of the reconstructed signals

由圖3～5對比可見，ONMF在分解冗余量較大的信號時能克服傳統NMF的缺點，表明了其在振動信號分離中的優勢。

5 應用實例

為驗證算法的有效性，采用滾動軸承振動實驗臺的振動加速度信號進行外環剝落故障特征的提取。其中，軸承型號ZA-2115，轉速為2 000 r/min，徑向負載26 695 N，在軸承座上通過PCB 353BB33高靈敏度ICP加速度傳感器獲取振動信號，采樣頻率為20 kHz。圖6和圖7為時域波形和時頻分布。由于噪聲干擾，振動信號波形中由故障引起的沖擊成分受到顯著影響。時頻分布中，能量分布集中在5 kHz以下，在部分頻帶有明顯的能量分布，如1.0 kHz，3.0～5.0 kHz，局部沖擊對應的特征應分布在這些頻率中。

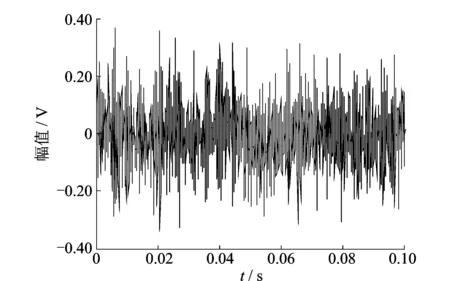
圖6 滾動軸承振動信號波形Fig.6 Vibration waveform of rolling element bearings

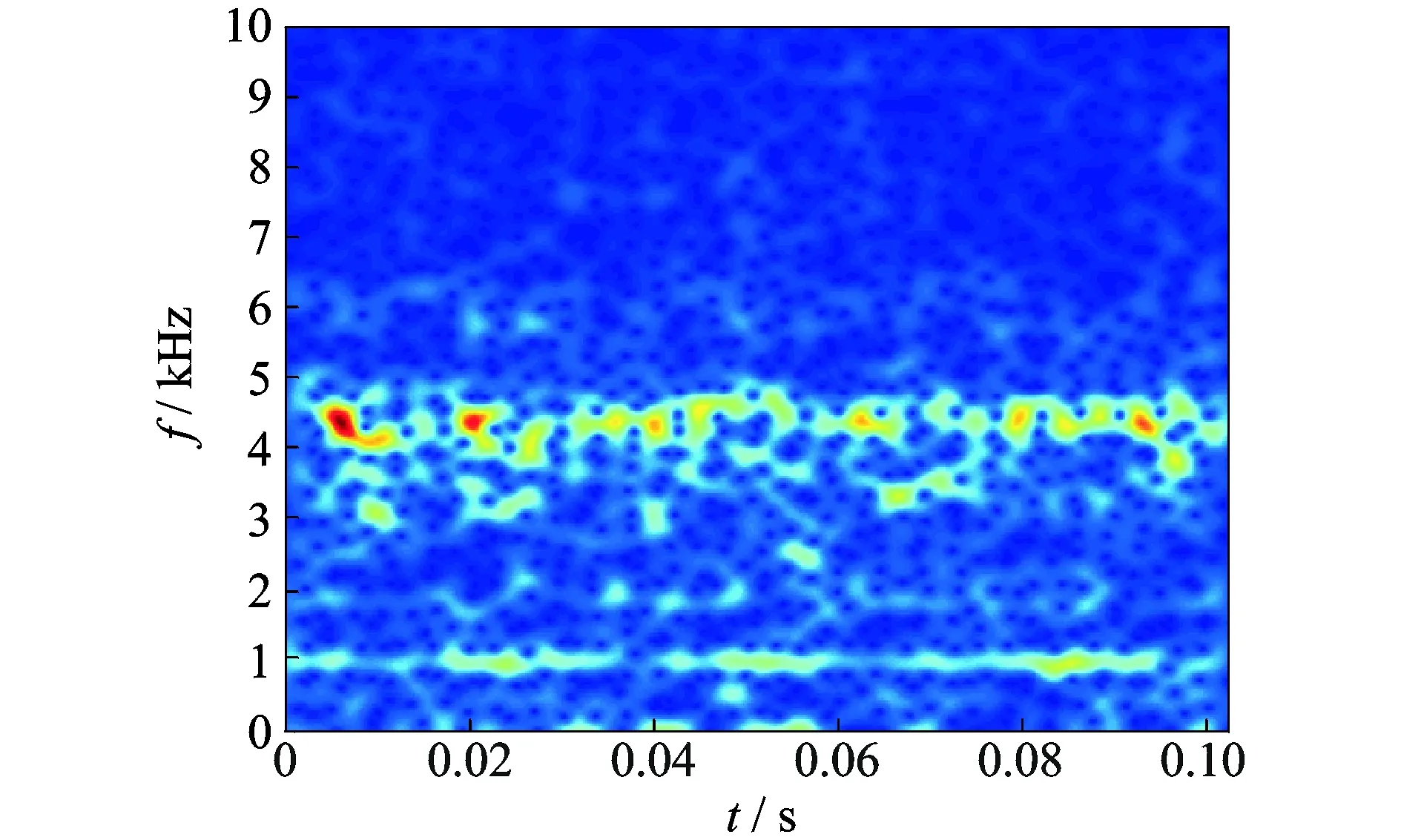
圖7 軸承振動信號的時頻分布Fig.7 Time-frequency distribution of vibration signal

采用ONMF方法分離沖擊特征，由圖8所示的核心一致性指標的變化曲線確定出最優子空間維數k=3。圖9～11為分離得到的3個子空間的幅度譜。同圖7所示的原始時頻分布對比可見，經過ONMF分解，特征被分解在不同的子空間中。其中：圖9所示的第1子空間中主要包含3.2和4.2 kHz兩個頻帶；圖10所示的第2子空間中主要是1.0和4.6 kHz頻帶；圖11所示的第3子空間具有較好的周期分布特點，對應著外環故障沖擊特征表現。因此，將第3子空間時頻分布對應的基向量和權向量進行重構，得到圖12所示的特征波形。

圖8 核心一致性指標的變化曲線Fig.8 The curve of consistency index

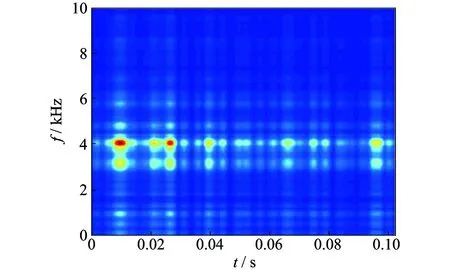
圖9 第1子空間時頻分布Fig.9 Time-frequency distribution of the first subspace

圖10 第2子空間時頻分布Fig.10 Time-frequency distribution of the second subspace

圖11 第3子空間時頻分布Fig.11 Time-frequency distribution of the third subspace

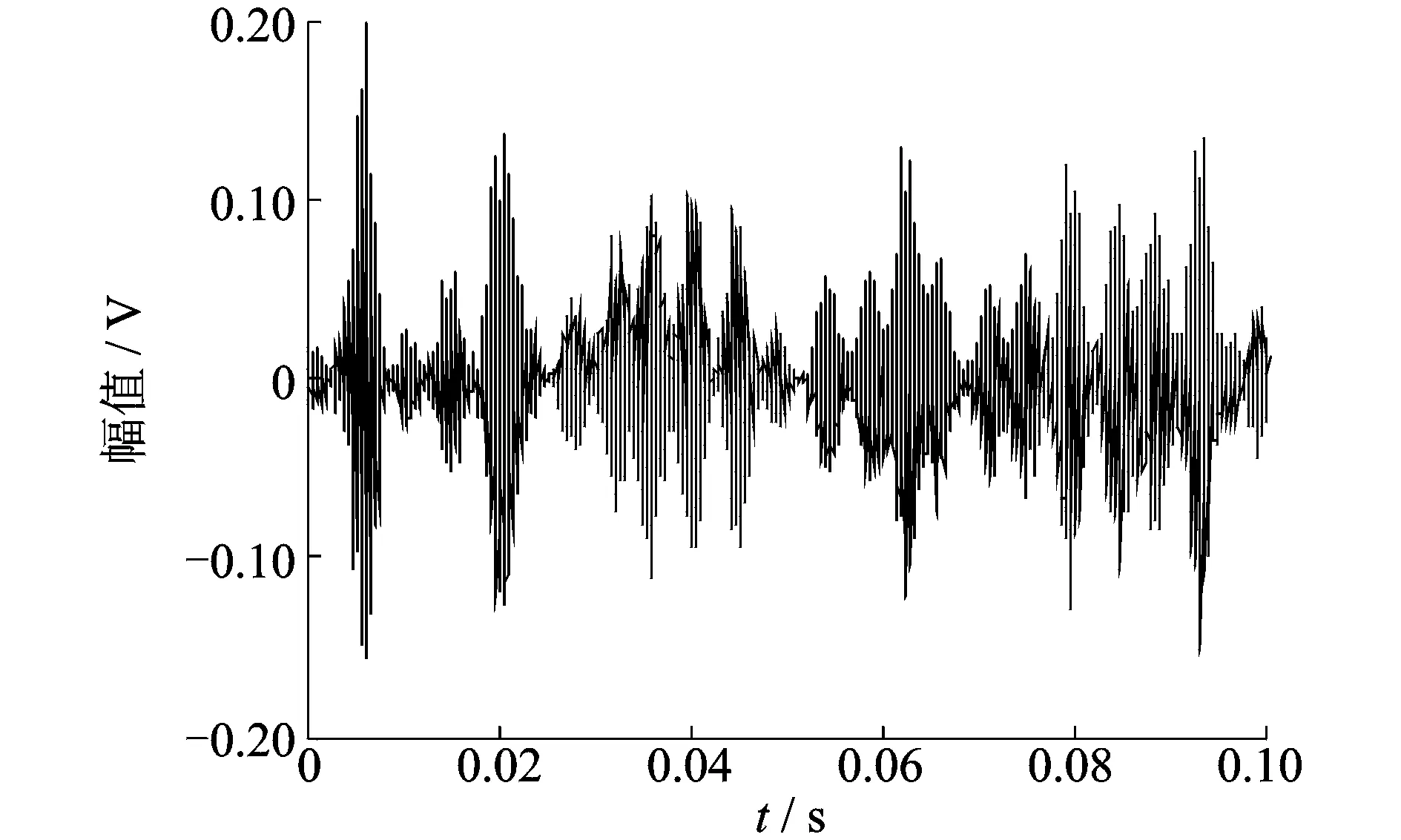
圖12 提取的特征波形Fig.12 Waveform of extraction feature

由圖6所示的原始波形信號對比可見，由外環故障引起的沖擊特征被有效地提取出來。經過ONMF分離提取之后，信號幅值譜有效地分離出了沖擊與噪聲，說明了所提方法處理實際數據的有效性。為了進一步驗證，選擇k=2時的特征分離做對比，所提取的特征波形如圖13所示。

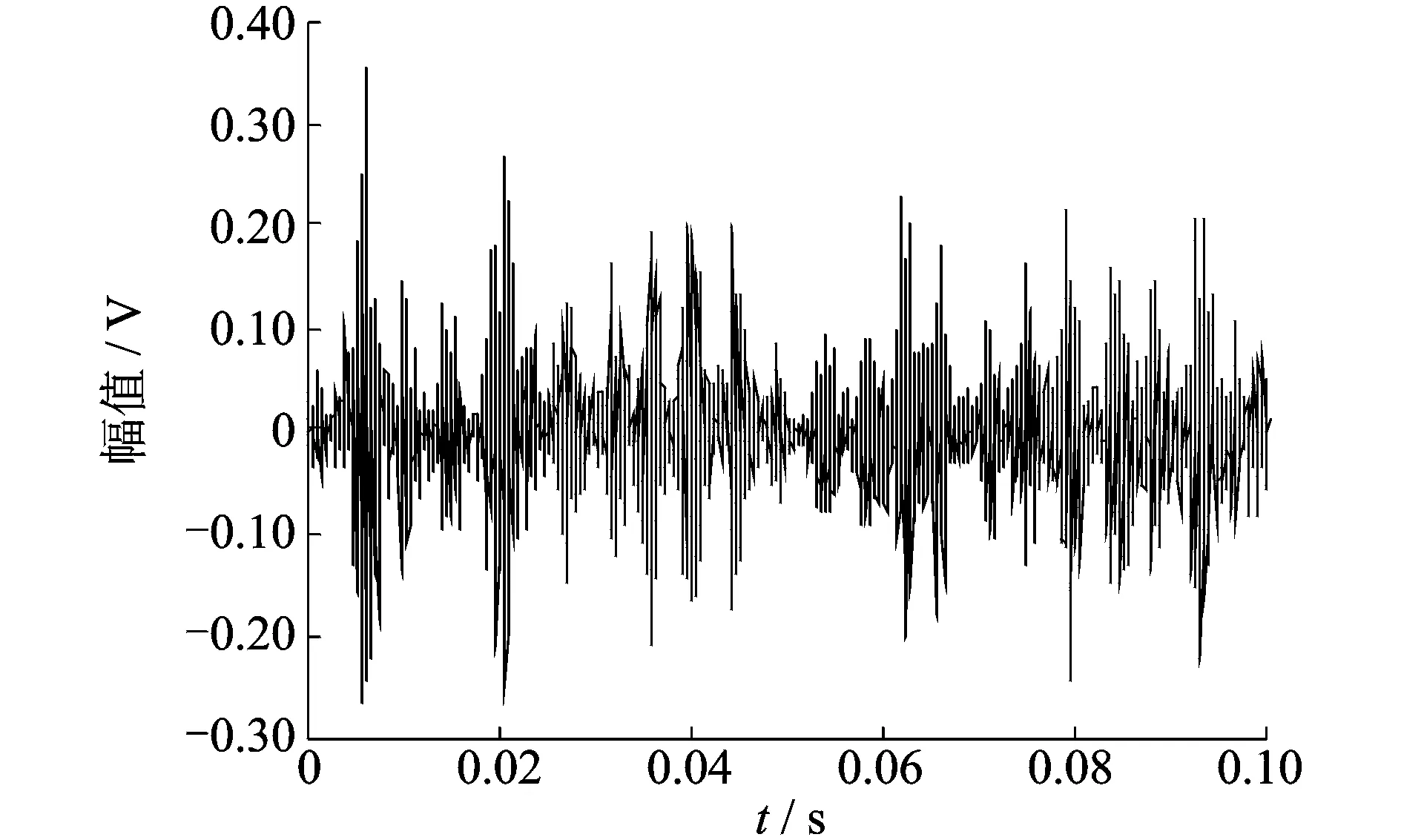
圖13 k=2時提取的特征波形Fig.13 Waveform of extraction feature with k=2

同圖12提取的時域波形對比分析可見，當子空間維數減少時，沖擊分量的波形中包含了其他的分量信息，導致提取的效果變差。對其子空間的時頻分布進行對比分析，發現除包含主要周期分量外，還含有大量的其他頻率分量，從而導致重構波形中含有更多的其他分量。由此可見，利用本算法能夠很好地提取出有效的局部故障特征。

6 結 論

1) 帶有正交性約束的ONMF方法用于單通道的源分離中，大大提高了所提取信息的獨立性，能夠更準確地描述源信號。

2) 根據振動信號的特點，引入核心一致性方法來評估觀測矩陣的隱含子空間維數，可以提高ONMF的分解效果，獲得較好的子空間時頻分布。

3) 通過STFT變換得到原始混合信號的幅值譜，在低維子空間中經過選擇及ISTFT重構，可以有效提取出局部故障導致沖擊特征的波形。因此，該方法對滾動軸承和齒輪箱等設備的早期故障檢測具有重要的意義，具有一定的工程應用價值。

[1] Sze C J，Liao H Y M，Fan K C.A new image flux conduction model and its application to selective image smoothing[J].IEEE Transactions on Image Processing，2001，10(2)：296-306.

[2] Tuzikov A V，Sheynin S A. Symmetry measure computation for convex polyhedra[J].Journal of Mathematical Imaging & Vision，2002，16(1)：41-56.

[3] Liu Haining，Liu Chengliang，Huang Yixiang. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J].Mechanical Systems and Signal Processing，2011，25(2)：558-574.

[4] Dong Shaojiang，Tang Baoping，Zhang Yan. A repeated single-channel mechanical signal blind separation method based on morphological filtering and singular value decomposition[J].Measurement，2012，45(8)：2052-2063.

[5] 劉婷婷，任興民.獨立分量分析在機械振動信號分離中的應用[J].振動、測試與診斷，2009，29(1)：36-41.

Liu Tingting，Ren Xingmin. Applying independent component analysis (ICA) to obtaining better blind separation of mechanical vibration signals[J]. Journal of Vibration，Measurement & Diagnosis，2009，29(1)：36-41. (in Chinese)

[6] 周曉峰，楊世錫，甘春標.一種旋轉機械振動信號的盲源分離消噪方法[J].振動、測試與診斷，2012，32(5)：714 -717.

Zhou Xiaofeng，Yang Shixi，Gan Chunbiao. A blind source separation denoising method of rotating machinery vibration signal[J].Journal of Vibration，Measurement & Diagnosis，2012，32(5)：714-717. (in Chinese)

[7] 劉維湘，鄭南寧，游屈波.非負矩陣分解及其在模式識別中的應用[J].科學通報，2006，51(3)：241-250.

Liu Weixiang，Zheng Nanning，You Qubo. Non negative matrix factorization and its applications in pattern recognition[J].Chinese Science Bulletin，2006，51(3)： 241-250. (in Chinese)

[8] 王科俊，左春婷.非負矩陣分解特征提取技術的研究進展[J].計算機應用研究，2014，31(4)：970-975.

Wang Kejun，Zuo Chunting. Improvements of non-negative matrix factorization for image extraction[J].Application Research of Computers，2014，31(4)：970-975. (in Chinese)

[9] Mehmood A，Damarla T，Sabatier J. Separation of human and animal seismic signatures using non-negative matrix factorization[J].Pattern Recognition Letters，2012，33(16)：2085-2093.

[10]Li Bing，Zhang Peilin，Liu Dongsheng，et al. Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transform and two-dimensional non-negative matrix factorization[J].Journal of Sound and Vibration，2011，330 (10)：2388-2399.

[11]Wang Qinghua，Zhang Youyun，Cai Lei，et al. Fault diagnosis for diesel valve trains based on non-negative matrix factorization and neural network ensemble[J]. Mechanical Systems and Signal Processing，2009，23(5)：1683-1695.

[12]李兵，高敏，張旭光. 用形態梯度法與非負矩陣分解的齒輪故障診斷[J]. 振動、測試與診斷，2014，34(2)：295-300.

Li Bing，Gao Min，Zhang Xuguang. Feature extraction for engine fault diagnosis by utilizing adaptive multi-scale morphological gradient and non-negative matrix factorization[J]. Journal of Vibration，Measurement & Diagnosis，2014，34(2)：295-300. (in Chinese)

[13]李兵，米雙山，劉鵬遠. 二維非負矩陣分解在齒輪故障診斷中的應用[J]. 振動、測試與診斷，2012，32(5)： 836-840.

Li Bing，Mi Shuangshan，Liu Pengyuan. Applying two-dimensional non negative matrix factorization to gear fault diagnosis[J]. Journal of Vibration，Measurement & Diagnosis，2012，32(5)：836-840. (in Chinese)

[14]Lee D D，Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature，1999，401(6755)：788-791.

[15]Cichocki A，Zdunek R，Phan A H，et al. Nonnegative matrix and tensor factorizations[M]. West Sussex：John Wiley & Sons Inc，2009：131-142.

[16]Ding Chris，Li Tao，Peng Wei，et al. Orthogonal nonnegative matrix t-factorizations for clustering[C]∥Proceedings of the 12th Association for Computing Machinery SIGKDD International Conference on Knowledge Discovery and Data Mining. Philadelphia，USA：ACM Press，2006：126-135.

[17]Li Zhao，Wu Xindong，Peng Hong. Nonnegative matrix factorization on orthogonal subspace[J]. Pattern Recognition Letters，2010，31 (9)：905-911.

[18]Cichocki A，He Zhaoshui. An efficient K-hyperplane clustering algorithm and its application to sparse component analysis[J]. Lecture Notes in Computer Science，2007，4492(1)：1032-1041.

10.16450/j.cnki.issn.1004-6801.2016.05.003

*國家自然科學基金資助項目(51575438)

2014-08-06；

2014-12-31

TH165.3

梁霖，男，1973年1月生，博士、副教授。主要研究方向為機械設備故障診斷技術。曾發表《沖擊故障特征提取的非線性流形學習方法》(《西安交通大學學報》2009年第43卷第11期)等論文。

E-mail: lianglin@xjtu.edu.cn。