基于一類二階線性變參系統特征結構配置的完全參數化方法

安博林

(東北電力大學自動化工程學院，吉林 吉林 132012)

基于一類二階線性變參系統特征結構配置的完全參數化方法

安博林

(東北電力大學自動化工程學院，吉林 吉林 132012)

二階線性時變參數系統 特征結構配置 比例微分控制律 航天器在軌加油

非線性系統在混沌運動控制[1]、最優控制[2]、模糊建模[3]、魯棒控制[4]及預測控制[5]等工程領域有著十分廣泛的應用前景。眾所周知，非線性系統的線性變參增益調度控制可以看作是線性控制技術向非線性控制技術的一種拓展[6,7]。在實際應用中許多非線性系統可以由線性變參系統代替。由于一個多變量線性變參系統的穩定和動態表現與該系統的特征結構配置息息相關，因此對于系統特征結構配置問題的研究在控制理論及其應用方面具有十分重要的意義。

考慮一類通過比例微分控制來解決其特征結構配置問題的二階線性變參系統：

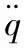
(1)

其中，q(t)是狀態向量,q(t)∈Rn；u(t)是輸入向量，u(t)∈Rr；θ(t)為時變參數向量，θ(t)=[θ1(t),θ2(t),…,θN(t)]T∈RN；A(θ)、B(θ)和C(θ)均為θ(t)的顯函數，A(θ)∈Rn×n，B(θ)∈Rn×r，C(θ)∈Rn×n，B(θ)為關于θ(t)的滿秩矩陣。

假設1 [A(θ)B(θ)]關于θ(t)為能控。

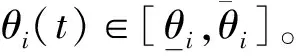
通過矩陣變換可以將二階線性變參系統(1)等效成一個一階線性變參系統：

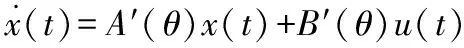
(2)

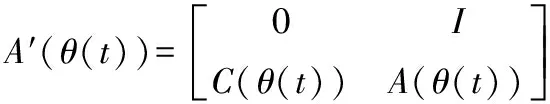
(3)

但是這不可避免地涉及到2n維矩陣的操作從而導致計算較為繁瑣，因此如何減少計算量，提出一個更為簡潔有效的方法成為了研究學者迫切需要解決的問題。

在矩陣對[A(θ)B(θ)]能控的前提下，筆者提供了一個通過比例微分反饋來解決二階線性變參系統特征結構配置問題的簡潔完整的參數化方法以及基于閉環特征值和一組參數向量的針對閉環特征向量和反饋增益的簡潔完整的參數化表達式。上述閉環特征值和參數是根據該閉環系統的各種需要所選取的。筆者提出的方法之所以簡潔是因為該方法的計算量主要集中在兩個多項式矩陣的化簡或者兩組在事先選取合適閉環特征值前提下的奇異值分解，而且只是直接利用原有系統的系數A(θ)、B(θ)和C(θ)，所涉及到的操作僅僅針對n維矩陣。

1 問題描述

比例微分控制律為：

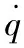
K(θ)=[K0(θ)K1(θ)]

(4)

將式(4)應用到系統(1)或(2)中，即可獲得如下形式的閉環系統：

(5)

其中，

Ac(θ(t))=A′(θ(t))+B′(θ(t)K(θ(t))

(6)

基于一般情形考慮，進行如下推導。

令Γ(θ)={si(θ),si(θ)∈C,i=1,2,…,n′，1≤n′≤2n}為矩陣Ac(θ)的一組特征值，并且該組特征值關于實軸對稱(共軛復數)。設上述特征值si(θ)的代數重數和幾何重數分別為mi和qi,則在矩陣Ac(θ)的Jordan標準型F(θ)中有qi個與特征值si(θ)相關的Jordan塊。若記這些Jordan塊的階數為pij，j=1,2,…,qi，則有：

(7)

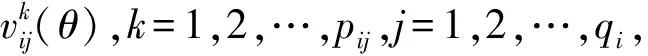
(8)

其中滿足式(7)的Γ(θ)和pij，qi，mi，i=1,2,…,n′，j=1,2,…，qi,可以描述成如下形式：

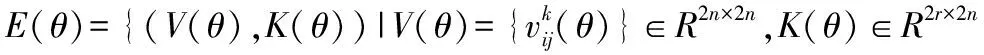
將式(8)轉換成如下參數化形式：

A′(θ)V(θ)+B′(θ)K(θ)V(θ)=V(θ)F(θ)

(9)

其中F(θ)∈R2n×2n為Ac(θ)的Jordan形式。

綜上所述，通過比例微分控制律(4)來解決二階線性變參系統(1)的特征結構配置問題(ESA)描述如下：

給出矩陣A(θ)、C(θ)∈Rn×n、B(θ)∈Rn×r和一系列共軛復數si,i=1,2,…,2n，找到所有滿足式(9)的矩陣K(θ)∈Rr×2n和V(θ)∈C2n×2n，其中det(V(θ))≠0且矩陣A′(θ)和B′(θ)均由式(3)構成。

筆者的主要目的就是在矩陣對[A(θ)B(θ)]能控的情況下，為解決二階線性變參系統(1)的特征結構配置問題提供一個操作過程直接針對原系統系數A(θ)、B(θ)和C(θ)的簡潔方法。

2 初步分析

眾所周知，當且僅當下式成立的前提下矩陣對[A(θ)B(θ)]才可以保證能控：

rank[A(θ)-sIB(θ)]=n,?s∈C

(10)

當式(10)成立時，則存在一對幺模矩陣P(θ，s)和Q(θ,s)滿足：

P(θ,s)[A(θ)-sIB(θ)]Q(θ,s)=[0I]

(11)

對Q(θ,s)進行如下分塊：

(12)

將K(θ)=W(θ)V-1(θ)代入到式(9)中得到如下Sylvester方程：

A′(θ)V(θ)+B′(θ)W(θ)=V(θ)F(θ)

(13)

因此二階線性變參系統的特征結構配置問題就轉化成了Sylvester方程(13)的求解問題，其中矩陣V(θ)∈Cn×p和W(θ)∈Cr×p即為所求。

引理1 令[A(θ)B(θ)]為能控，則式(13)所有的解決方案可以歸納為如下形式：

(14)

或者等效為：

vi(θ)=Q12(θ,si(θ))P(θ,si(θ))ri+Q11(θ,

si(θ))fi(θ)

wi(θ)=Q22(θ,si(θ))P(θ,si(θ))ri+Q12(θ,

si(θ))fi(θ)

(15)

i=1,2,…,p

其中fi(θ)∈Cr,i=1,2,…,p為一組任意參數向量。

構建一組能控的矩陣對[A′(θ)B′(θ)]，則下述結論成立。

引理2 若[A(θ)B(θ)]為能控，則所構建的矩陣對[A′(θ)B′(θ)]也是能控的，當且僅當如下條件滿足時：

rank[Q12(θ,s)P(θ,s)C(θ)+sInQ11(θ,s)]=n,

?s∈C

(16)

同時式(16)也可以等效為存在一組幺模矩陣H(θ,s)和L(θ,s)，滿足：

H(θ,s)[Q12(θ,s)P(θ,s)C(θ)+sIn-Q11(θ,s)]·

L(θ,s)=[0In]

(17)

并將式(17)中的多項式矩陣L(θ,s)分塊成如下形式：

(18)

然后引出下面的定理。

引理3 假設式(17)對于幺模矩陣H(θ,s)和L(θ,s)均成立，則存在所有向量y(θ)和z(θ)滿足：

[Q12(θ,s)P(θ,s)C(θ)+sIn]y(θ)-Q11(θ,s)z(θ)=0

(19)

其中y(θ)、z(θ)滿足如下條件：

y(θ)=L11(θ,s)g(θ),z(θ)=L21(θ,s)g(θ)

(20)

且g(θ)∈Cr為任意參數向量。

3 ESA問題的解決方案

設

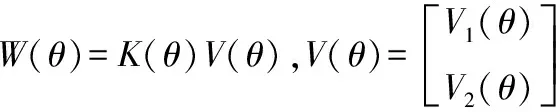
(21)

則式(9)可以被分解為如下形式：

V2(θ)=V1(θ)F(θ)

(22)

A(θ)V2(θ)+B(θ)W(θ)=V2(θ)F(θ)-C(θ)V1(θ)

(23)

由此可得式(23)符合式(13)形式，根據引理1得：

V2i(θ)=-Q12(θ,si(θ))P(θ,si(θ))C(θ)v1i(θ)+

Q11(θ,si(θ))fi(θ),i=1,2,…,2n

(24)

wi(θ)=-Q22(θ,si(θ))P(θ,si(θ))C(θ)v1i(θ)+

Q21(θ,si(θ))fi(θ),i=1,2,…,2n

(25)

式(22)可以等效寫成如下形式：

v2i(θ)=si(θ)v1i(θ),i=1,2,…,2n

(26)

式(24)和式(26)聯立可得：

[Q12(θ,si(θ))P(θ,si(θ))C(θ)+si(θ)In]v1i(θ)-Q11(θ,si(θ))fi(θ)=0,i=1,2,…,2n

(27)

由于式(27)符合式(19)的形式，則根據引理3可得：

v1i(θ)=L11(θ,si(θ))gi(θ),i=1,2,…,2n

(28)

fi(θ)=L21(θ,si(θ))gi(θ),i=1,2,…,2n

(29)

其中gi(θ)∈Cr,i=1,2,…,2n為一組任意參數向量。

將式(28)代入式(26)中可得：

v2i(θ)=si(θ)L11(θ,si(θ))gi(θ),i=1,2,…,2n

(30)

此外，將式(28)、(29)代入式(25)中，可以得到向量wi(θ),i=1,2,…,2n和參數向量gi(θ),i=1,2,…,2n的表達式。因此，可以獲得如下定理來求解該系統的ESA問題。

定理1 若[A(θ)B(θ)]和[A(θ)′B′(θ)]均為能控，則綜合上述推理可以得到該系統特征結構配置問題的求解方案：

(31)

K(θ)=W(θ)V-1(θ)

(32)

其中矩陣W(θ)由wi(θ)構成：

wi(θ)=[Q21(θ,si(θ))L21(θ,si(θ))-Q22(θ,si(θ))·P(θ,si(θ))C(θ)L11(θ,si(θ))]gi(θ),i=1,2,…,2n

(33)

且gi(θ)∈Cr(i=1,2,…,2n)是一組滿足下述約束條件的參數向量：

約束條件C2 det[V]≠0

上述定理中的約束條件C1是為了保證式(21)或式(32)中的矩陣K(θ)為實。

4 數值算例

參考一個在文獻[8]中提供的航天器在軌加油的一般過程，該航天器在軌加油的姿態動力學模型可以表示成如下形式：

(34)

其中φ(t)、φ(t)、ψ(t)表示航天器的俯仰角、滾動角、偏航角；ω0表示軌道角速度；Ix(t)、Iy(t)、Iz(t)表示航天器的轉動慣量I(t)在坐標系下的各軸分量；Ux、Uy、Uz表示航天器在坐標系各軸上的力矩分量。

先通過矩陣變換求得模型(34)滿足式(1)的參數矩陣：

(35)

q=[φ(t)φ(t)ψ(t)]T為狀態向量，u=[UxUyUz]T為輸入向量，而θ=[Ix(t)Iy(t)Iz(t)]T為時變參數向量。矩陣對[A(θ)B(θ)]和[A′(θ)B′(θ)](由式(3)定義)在該系統中均為能控。

通過計算易得一組滿足式(11)的幺模矩陣P(θ,s)和Q(θ,s)：

P(θ,s)=diag[1 1 1]

(36)

(37)

同時還可以獲得一組滿足式(17)的幺模矩陣H(θ,s)和L(θ,s)：

H(θ,s)=diag[1 1 1]

(38)

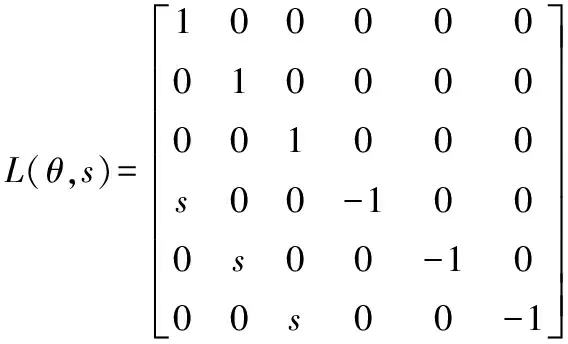
(39)

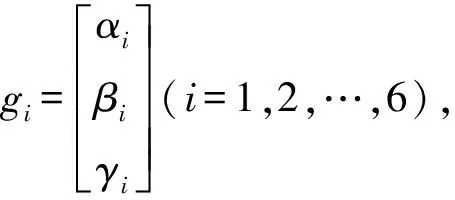
V=[αiβiγisiαisiβisiγi]T,i=1,2,…,6

(40)

進一步由式(33)可以求得矩陣W(θ,s)：

(41)

眾所周知，如果一個矩陣的Jordan型是一個對角矩陣，那么該矩陣的特征值對于矩陣中的參數擾動并不敏感。因此，出于魯棒性和減少對參數擾動敏感性的考慮，選取不同的閉環系統特征值如下：

(42)

其中由式(35)給出的aij和bij均為關于時變參數向量θ[Ix(t)Iy(t)Iz(t)]T的函數。

將所設計的狀態反饋控制器(42)應用到航天器在軌加油姿態控制系統模型(34)當中去。假設該航天器的姿態角速度均為0°/s(即0rad/s)，初始姿態角均為1°(即0.0175rad),在初始狀態下，x(0)=[0 0.0175 0 0.0175 0 0.0175]T閉環系統3個姿態角的初始值響應和仿真結果如圖1所示。從圖中可以看出，3個姿態角的時間響應變化迅速且穩態誤差最終趨于0。

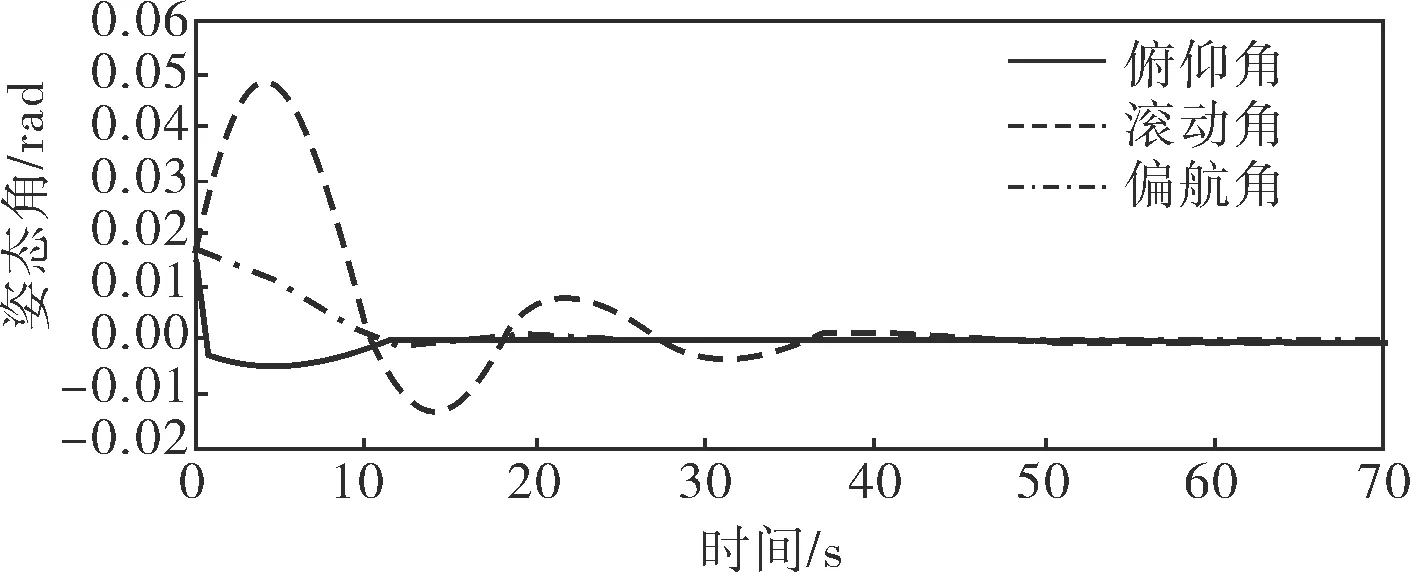
圖1 姿態角的時間響應

仿真結果表明：所獲得的比例微分控制律保證了所設計的閉環系統的穩定性，同時也驗證了前文推導出的算法的有效性和實用性。

5 結束語

解決了一類基于比例微分控制律的二階線性變參系統的特征結構配置問題，并提出了兩個分別針對閉環特征向量矩陣和反饋增益的簡潔完整的參數化表達式。上述主要的操作過程在于兩組初等矩陣的變換或者兩組奇異值分解，計算量僅僅涉及到n維矩陣。然后選取合適的自由參量和閉環特征值來獲得滿足系統要求的比例微分控制律。最終通過一個航天器在軌加油姿態控制系統模型來驗證所推導出的線性變參控制方法的實用性和有效性，同時從仿真結果中可以得出上述線性變參控制律保證了所設計閉環系統的穩定性并提供了良好的性能。

[1] 韓明君，李有堂，朱麗，等.干氣密封系統軸向非線性動力穩定性[J].化工機械，2012，39(3)：308～312.

[2] 高德欣，楊曉燕.受擾動非線性系統的反饋線性化最優控制[J].化工自動化及儀表，2010，37(8)：19～22.

[3] 趙艷東，任憲勇，張興隆，等.基于階躍模型的非線性模糊PID控制算法研究[J].化工自動化及儀表，2010，37(7)：28～31.

[4] 周碩.一類非線性不確定時滯系統魯棒預測控制[J].化工自動化及儀表，2011，38(2)：149～152.

[5] 張燕，申森.基于快速正交搜索算法的非線性預測控制[J].化工自動化及儀表，2014，41(11)：1226～1244.

[6] Rugh W J,Shamma J S.Research on Gain Scheduling[J].Automatica,2000,36(10)：1401～1425.

[7] Leith D J,Leithead W E.Survey of Gain-scheduling Analysis and Design[J].International Journal of Control,2000,73(11)：1001～1025.

[8] 張龍.航天器在軌加注的姿態動力學與控制[D].哈爾濱:哈爾濱工業大學，2009.

(Continued on Page 538)

CompletelyParameterizedApproachforEigenstructureAssignmentinSecond-orderLinearParameter-varyingSystem

AN Bo-lin

(SchoolofAutomationEngineering,NortheastDianliUniversity,Jilin132012，China)

TP13

A

1000-3932(2016)05-0457-06

2016-04-06(修改稿)