基于改進的模糊C-均值聚類算法的接線箱分配設計與應用

劉迪成 王 建 王敏昊

(中國海誠工程科技股份有限公司，上海 200031)

基于改進的模糊C-均值聚類算法的接線箱分配設計與應用

劉迪成 王 建 王敏昊

(中國海誠工程科技股份有限公司，上海 200031)

為了解決工程設計中接線箱分配最優化的問題，通過分析和比較各種聚類方法，對模糊C-均值聚類算法進行改進和參數設置，通過初始化、迭代、解模糊及分裂等步驟，實現了接線箱的自動分配功能。并設計了一種基于改進的模糊C-均值聚類算法的接線箱分配輔助軟件，可以根據不同要求自動分配接線箱的功能，給出了軟件流程，分析了實驗結果，并在某設計院項目接線箱的實際布置中成功應用。

模糊C-均值聚類 接線箱自動分配 模糊聚類 軟件流程

工程設計流程具有事情多、時間緊、任務重的特點。其中，接線箱分配是工程設計中重要的一環，需要考慮箱柜的位置、數量及電纜的總長度等問題，這不僅占用了工程師大量的時間，同時由于所涉及的數據量巨大，即使有經驗的工程師也很難做到線纜布置的最優化，而由于不同的配線方案所產生的電纜變化量往往能達到10%～20%，這不僅直接影響到工程造價，而且效率低、浪費嚴重。因此，解決接線箱的優化分配設計問題具有重要的實際意義。

聚類，就是把具有相似性質的事物區分開來加以分類。聚類分析就是用數學方法研究和處理給定對象的分類。模糊聚類建立了樣本對類別的不確定性描述，能夠有效地對類與類之間交叉的數據集進行聚類，能夠更客觀地反映現實世界，因而成為聚類分析研究的主流。模糊聚類算法作為應用最廣泛的聚類算法之一，具有簡單、收斂速度快及能夠處理大規模數據等優點，因此，該算法不僅被有效地應用于數據挖掘、模式識別及決策支持等領域[1,2]，在工程設計領域也有著廣泛的應用。如耿志強和朱群雄將C-means聚類應用于乙烯裂解爐的生產過程優化中，通過引入Mercer條件的核函數，克服模糊C-均值聚類在各分量方差分布不均或交叉分布情況下存在的錯分現象[3]；劉遠紅等利用k-means聚類算法識別原油油水界面[4]；周強和韓九強將動態聚類用于紙張緊度的在線檢測，通過K均值聚類算法預處理訓練樣本，以平滑優化途徑[5]；俞樹榮等結合模糊聚類方法與人工神經網絡技術，提高了壓力容器安全評定的可靠性和水平[6]。

在接線箱優化分配設計過程中，由于每個接線箱中端子排的數量、每個端子排的端子數都有設定的最大值，因此屬于每一類樣本數固定，而分類數不確定的動態模糊聚類。然而，由于閾值無法確定，無法簡單地基于模糊等價矩陣按要求做到有效的分類。模糊C-均值(FCM)聚類是最為經典的分類數給定的聚類算法[7，8]，但也有著很大的局限性，如聚類數、聚類初始中心和加權指數的選擇都極大地影響著聚類效果[9，10]。筆者針對工程設計中接線箱優化分配的實際問題，提出一種基于改進的模糊C-均值聚類的接線箱最優分配模型。改進了文獻[7，8]中的模糊C-均值聚類算法，同時進行參數設置，將分配問題轉換為目標函數的優化問題，給出了求解算法，還給出了基于改進模糊C-均值聚類算法的接線箱分配輔助軟件流程的設計方案，并分析了實驗結果。

1 FCM聚類算法

FCM將n個向量分成c個模糊組，定義每一個類有一個聚類中心，再根據向量與聚類中心的距離，形成隸屬度的模糊數據集，其和總等于1，即：

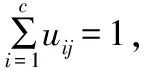
(1)

(2)

利用拉格朗日乘數法，得出最佳模糊隸屬度矩陣uij和對應的聚類中心ci的計算式如下：

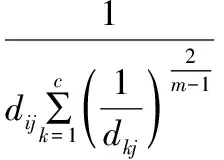
(3)

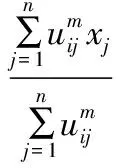
(4)

FCM算法是一個簡單的迭代過程，其步驟如下：

a. 初始化聚類中心；

b. 根據式(3)計算模糊隸屬度矩陣；

c. 根據式(4)計算新的聚類中心；

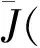
2 FCM聚類算法的參數設置與算法改進

影響FCM聚類算法的重要參數有兩個，在進行接線箱分配時，二者的設置方法具體如下：

a. 對于加權模糊指數m的設置，Bezdek給出的經驗范圍是1≤m≤5；此后又得到m=2時FCM算法的物理解釋，認為m=2最合適[11]。

b. 對于分類數c，由總樣本個數與每個聚類點最大值相除進行估算，即將初始目標設定為盡量使用最少的接線箱個數。

在FCM聚類算法迭代結束后，每個聚類中的樣本個數不一定滿足小于最大值的要求。對此，可以通過兩種方法予以解決：第1種是對每一個聚類點進行解模糊運算時，當一個聚類點數量已滿后，將其他本屬于該聚類點的樣本放入下一個最近的聚類點(即一個接線箱放滿后，將放不下的測量點分配至下一個最近的接線箱)；第2種方法是解模糊后，對聚類進行分裂處理，將超過最大值的聚類分成多個。顯然，第1種方法可以得到更少的聚類點數量(即接線箱數量)，第2種方法可以得到更小的價值函數值(即電纜總長度)。在實際工程中，權衡接線箱和電纜的成本后，再決定所使用的方法。

對于初始聚類中心的選取，由于該算法對初始點的依賴大，如果初始分類選擇不當，將會收斂成為一個局部最小的函數，導致結果不穩定[12～14]。通過密度法選擇初始聚類中心，首先計算每個樣本的密度(即以該樣本為中心的一個球形區域內樣本點的個數)，選取密度最大的樣本作為第1個初始聚類中心；然后在離開第1個初始聚類中心的球形區域外，選擇密度第2大的點作為第2個聚類中心，這樣就避免了聚類中心過分集中的現象。依此類推，選出所有的初始聚類中心。

3 系統實現

3.1系統結構

基于改進的模糊C-均值聚類算法的接線箱分配系統的軟件流程(圖1)分為兩個步驟：首先通過模糊C-均值算法將測量點聚類成端子排；然后通過同樣的算法將端子排聚類成接線箱。

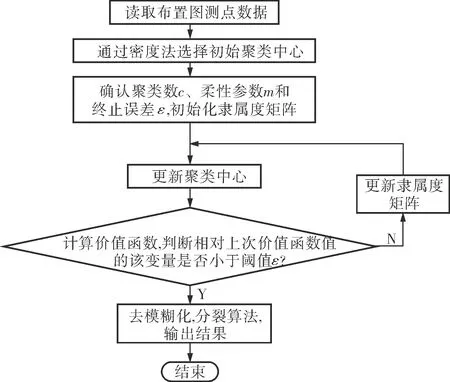
圖1 基于改進的模糊C-均值聚類算法的接線箱分配系統程序流程

3.2軟件實現

基于改進的模糊C-均值聚類算法的接線箱分配系統軟件采用VBA語言編寫，適用于Windows平臺。在實際應用中，該軟件在AutoCAD下運行，采用Access作為數據庫進行數據處理。工程師在對話框輸入對現場接線箱的要求，該軟件將根據要求讀取布置圖中的測量點信息，寫入Access數據庫；然后通過改進的FCM算法得出接線箱的數量、分配和布置。

先由工程師輸入設計需求：模擬量輸入(AI)、輸出(AO)信號是否可在同一個端子排中；能否包含三線制溫度計(RTD)的端子排；模擬量信號和數字量信號能否放進同一個接線箱；每個端子排最多包含的回路數；每個接線箱最多包含的端子排數；電磁閥箱最多包含的回路數等信息。按照上述要求實現的界面如圖2所示。

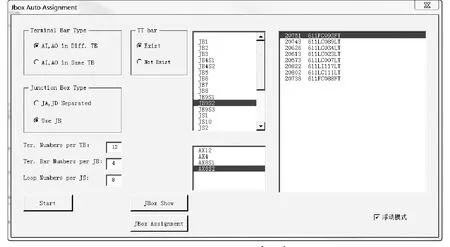
圖2 箱柜分配清單界面

通過自動運算可以得出箱柜清單、每個箱柜中端子排的清單和每個端子排上的儀表清單，并在布置圖中標示出接線箱的參考位置，為設計提供決策支持，如圖3所示。

圖3 箱柜參考位置

4 運行結果分析

使用某項目手工進行接線箱分配的結果與基于改進模糊C-均值聚類算法的分配結果進行比較，詳見表1。在實際測試中，歐氏距離和電纜長度之間存在相當高的一致性，使用基于改進的模糊C-均值聚類算法的計算結果比人工分配節省了10%～15%的電纜，并得到了更優化的分配方案。

表1 手工與改進FCM接線箱分配結果對比

以某項目中電磁閥箱的分類為例，圖4、5分別表示手工分配和改進的模糊C-均值聚類算法分析的效果。可以明顯看出，使用本軟件后，樣本根據空間中的位置被有效分割。

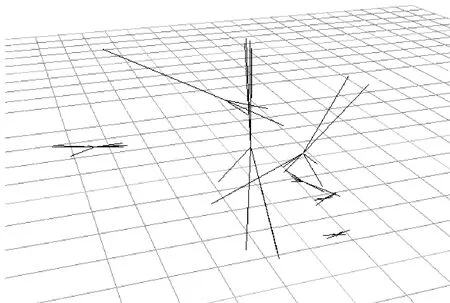
圖4 人工聚類結果

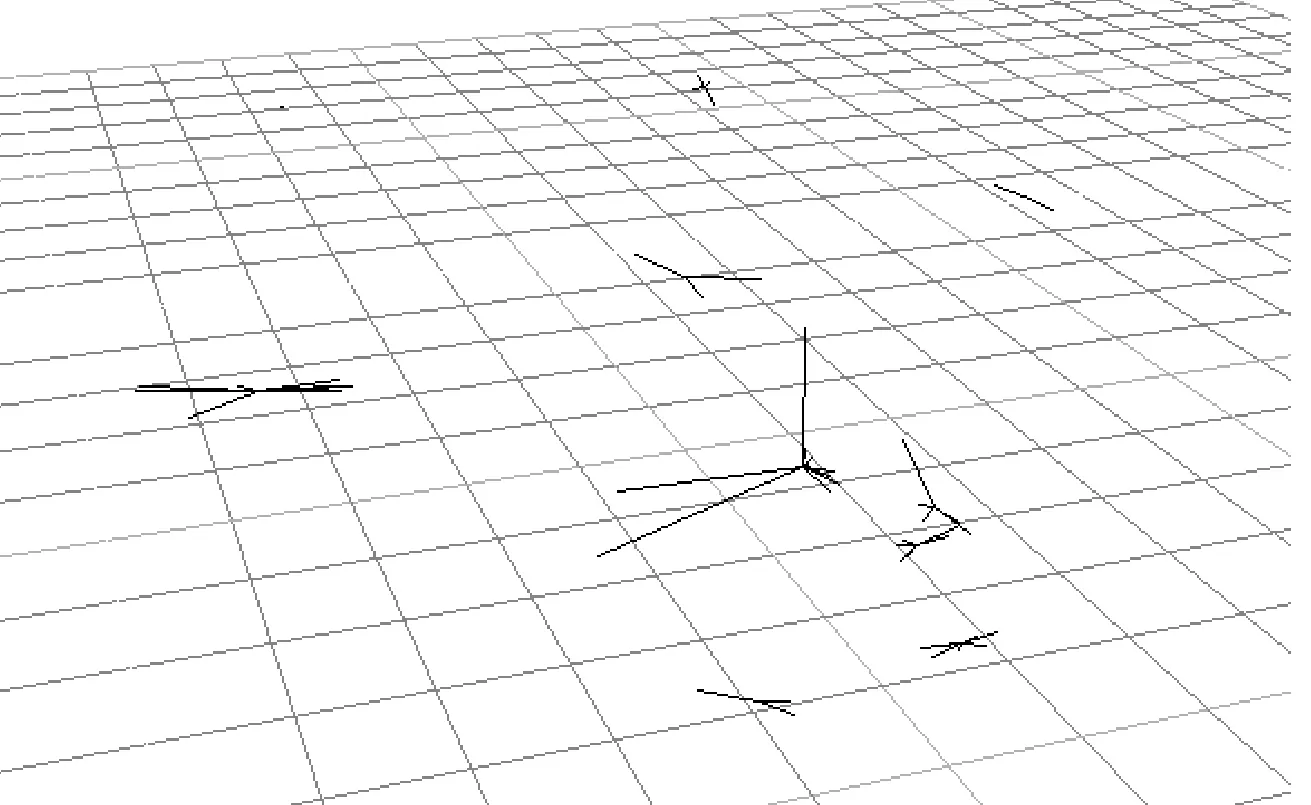
圖5 改進的模糊C-均值聚類結果

5 結束語

根據某設計院實際項目接線箱的布置圖數據，采用改進的模糊C-均值聚類算法對它進行分類，得到隸屬度矩陣和聚類中心。根據隸屬度矩陣進行分類，克服了人工分類方法效率低、主觀隨意性強、速度緩慢及無法得出最優解等問題。另外，通過該軟件計算出來的聚類點坐標，可以就近確定接線箱的位置，提高了施工圖設計效率，節省了項目成本。基于改進的模糊C-均值聚類的接線箱分配系統，對接線箱優化分配設計的方法具有一定的通用性和擴展性。

[1] Bezdek J C,Robert E,William F.The Fuzzy C-Means Clustering Algorithm[J].Computers and Geosciences,1994,10(2):191～203.

[2] Dave R N.Robust Fuzzy Clustering Algorithms[C].Second IEEE International Conference on Fuzzy System.San Francisco:IEEE,1993:1281～1286.

[3] 耿志強,朱群雄.動態核聚類算法在乙烯生產中的優化模式識別[J].化工自動化及儀表,2005,32(2):5～8.

[4] 劉遠紅,習玉陽,吳華遠,等.k-means聚類算法在油水界面檢測中的應用[J].化工自動化及儀表,2014,41(1):19～21.

[5] 周強,韓九強.基于動態聚類算法的CWNN在紙張緊度檢測中的應用[J].化工自動化及儀表,2006,33(4):14～18.

[6] 俞樹榮,李爾國,梁瑞.基于人工神經網絡的壓力容器安全評定可靠度的模糊分析[J].化工機械,2000,27(6):333～335.

[7] Dunn J C.A Fuzzy Relative of the ISODATA Process and Its Use in Detectiong Compact Well-separated Clusters[J].Journal of Cybernetics,1973,3(3):32～57.

[8] Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York:Plenum Press,1981.

[9] 高新波,謝維信.模糊C-均值聚類算法中加權指數m的研究[J].電子學報,2000,28(4):80～83.

[10] 張姣玲.利用FCM求解最佳聚類數的算法[J].計算機工程與應用,2008,44(22):65～67.

[11] Castleman K R,著,朱志剛,林學閆,石定機,等,譯.數字圖像處理[M].北京:電子工業出版社,1998:378～379.

[12] Bradley P S,Fayyad U M.Refining Initial Points for k-Means Clustering[C].Proceedings of the 15th International Conference on Machine Learning.San Francisco:Morgan Kaufmann,1998:91～99.

[13] Berkhin P.Survey of Clustering Data Mining Techniques[M].San Jose:Accrue Software Inc,2002.

[14] Duda R O,Hart P E.Pattern Classification and Scene Analysis[M].New York:Wiley,1973.

JunctionBoxesAllocationandApplicationBasedonImprovedFuzzyC-meansClusteringAlgorithm

LIU Di-cheng, WANG Jian, WANG Min-hao

(ChinaHaisumEngineeringCo.,Ltd.,Shanghai200031,China)

To optimize the allocation of junction boxes in engineering design, various clustering methods were analyzed and compared; and fuzzy C-means clustering algorithm was improved and relevant parameters were set; through initialization, iteration, defuzzification and split operation, the auto-allocation of junction boxes was realized. An improved C-means clustering algorithm-based assistive software for the auto-allocation of junction boxes was developed to allocate junction boxes as requested automatically; and the software flow chart was presented, including experimental results. This software enjoys successfully application in a design institute.

fuzzy C-means clustering,auto-allocation of junction boxes, fuzzy clustering, software flow chart

TH862+.7

B

1000-3932(2016)09-0962-04

2016-06-11(修改稿)