有關“三角形分割塊數”問題的透視— —對《三角形與多邊形分割》兩篇文章的思考

江蘇省蘇州市工業園區婁葑學校 崔志剛

有關“三角形分割塊數”問題的透視— —對《三角形與多邊形分割》兩篇文章的思考

江蘇省蘇州市工業園區婁葑學校 崔志剛

一、描述一下這類問題的內容及它的來龍去脈

第一篇文章簡介：王海燕、王學賢、王申懷三位同志的《三角形與多邊形的分割》［1］提出這樣一個問題：把一個三角形各邊n等分，連接各頂點和諸分點的線段，把三角形分割為多少塊？

原文《三角形與多邊形的分割》提出分割的塊數公式

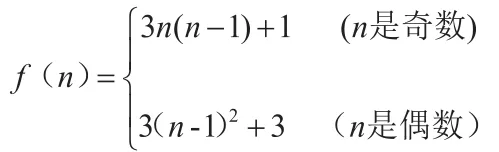
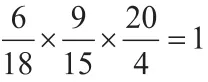
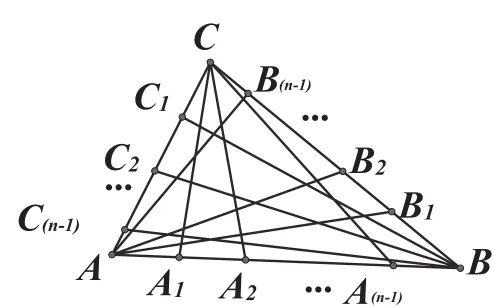
二、我在他們的基礎上我提出一個解決這類問題的完整的看法，并回答相關的問題。

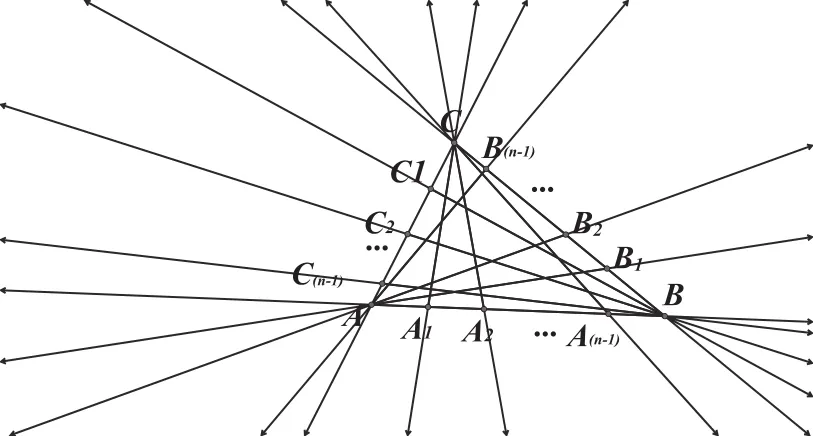
假如每邊不是等份的話，那么可以實現任意三條分割線都沒有交點，此時可分的塊數計算（如圖），我們可以把每條邊和分割線延長為直線，拓展到整個平面內來思考。此時思路用整個3n條直線在沒有共點的情況下可分為的塊數減去三個頂點A、B、C處因共點而減少的塊數再減去三角形外的塊數即可得三角形內部被分為的塊數。

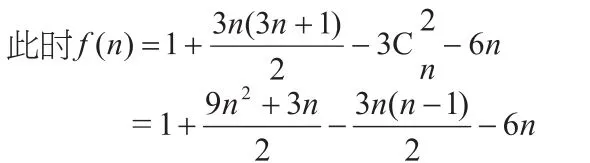
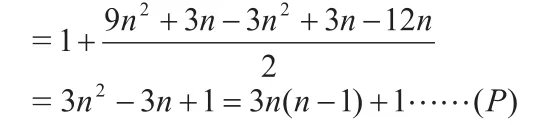
那么在有三線共點的情況下，每出現一次，就減去一塊。

在分割線有至少一條中線的情況下，有哪些共點的情況呢？

除中線外，其他的非中線的分割線討論情況如何尋找呢？用死方法一個一個試，肯定很煩，不太實用。下面我們用尋找質因數的方法來解決。

下面以n=40為例。其質因數有2個：2、5；故可知（R）式的分子分母之和為20、8，其（R）式的分數可能為：

（1）當分子分母之和為20時，其可能的分數分別為：

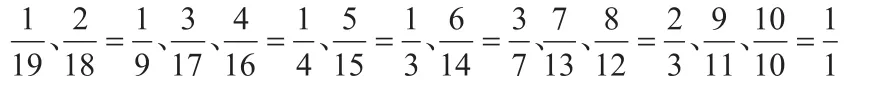
通過（1）、（2）中的分數的組合（可以重復使用、可以將分數的分子分母顛倒計算）

可得24種三線共點情況。

如果考慮中線的情況，根據（Q）式可知有115種三線共點情況，故每邊40等分時共可將三角形分割的塊數為=4541塊。

顯然可知：如何準確地計算每邊n等分后分割的塊數不可能有一個具體的公式，因為關于一個數的因數，數論中沒有一個明確的公式將一個數準確地分解為幾個質因數的積；只能說用以上的方法可以求出來，但無法通過一個具體的公式求出三線共點的情況。

那么，如何能夠知道n為哪些值的情況下有三線共點的情況呢？顯然所有的偶數都有中線，因而都存在三線共點的情況。除了中線外，n為偶數時還有沒有其他的呢？奇數呢？我們利用Excel采用如下的情況可以發現最小的奇數n為15，最小的偶數為20而不是文［2］所說的24，而且文章所列舉的奇數、偶數還有很多。奇數有：15、35、45、55、63、65、75、85、91、99、105；偶數有：20、24、30、40、42、48、56、60、66、70、72、80、84、90、96、100。至于更大的n值，需要Excel計算的量更大即可解決。

［1］王海燕等.三角形與多邊形分割［J］.數學通報，2006（08）.

［2］史立新等.《三角形與多邊形的分割》一文的錯漏［J］.數學通報，2012（04）.