基于誤差修正時間序列模型的短期電力需求預測分析

王飛燕

（蘭州財經大學，甘肅 蘭州 730000）

基于誤差修正時間序列模型的短期電力需求預測分析

王飛燕

（蘭州財經大學，甘肅 蘭州 730000）

隨著經濟、社會和工業的快速發展，電力需求突飛猛進.電力行業也逐漸成為影響全球社會經濟發展地位的重要的因素，不準確的需求預測增加了電力行業的運行成本，特別是在市場環境中，精度即意味著金錢，準確的電力需求預測是有價值的。本文主要對許昌市短期電力需求進行分析預測，利用許昌市用電量的相關數據，分別應用移動平均法、時間序列法建立模型并對模型進行預測和分析，再通過對這兩種預測方法分別賦予不同的權重建立加權組合預測模型來改進預測誤差，通過比較分析得出加權組合模型預測的精度更高。

移動平均法；電力需求預測；時間序列法；加權組合預測法

隨著經濟的快速發展，世界各國對能源的需求量也日益增加，再加上電力資源清潔、經濟適用以及比較方便等優點，因此，各國都在致力于不斷提高本國的電氣化程度，從而來改善人民的生活并促進經濟的發展。與此同時，黨的十八大也對新一時期電力能源的發展做出了總部署，并提出“控制能源消費總量，加強節能降耗，支持節能低碳產業和新能源、可再生能源發展，確保國家能源安全”等要求。當前，我國為加強區域電力建設引入電力市場管理模式，通過對區域電力需求做出科學的分析和預測，以此來保證區域經濟穩定并且健康地發展。

1　背景介紹

電力需求的短期預測是組成電力系統發電計劃的重要部分，電力需求預測的結果是電力系統正常運行工作的基礎數據，其預測的精度可直接影響電力系統運行的經濟性及安全性，所以任何時候的首要任務均是要準確地預測電力需求量，因此，電力需求預測，尤其是短期、超短期預測是電力系統安全和經濟穩定發展的前提與保障。電力需求的短期預測同時也是電力公司制定生產計劃并進行發展規劃的重要依據，且準確的電力需求預測在保證用電需求以及增強供電可靠性的基礎上能夠有效地降低發電成本，故不準確的需求預測增加了電力行業的運行成本，特別是在市場環境中，精度即意味著金錢。與此同時，電力需求增加的有效的預警對于確保供給和需求之間的平衡也是非常重要的。因此，電力系統可以通過開發一個對電力需求的跳讀算法實現優化。

另外研究電力需求的其他原因，首先便是二氧化碳的排放，煤和燃煤電力是典型的向上流和向下流行業，由煤炭消耗產生的熱能和巨大的環境壓力不容忽視，因為發電的高比例，中國排放的熱能約占總二氧化碳排放量的。因此，準確和及時的電力需求預測可以為合理發電計劃與調整電力政策和結構提供可靠的依據，并大大減少二氧化碳排放量。其次，輸電網格安全影響國家安全，網格在許多國家經常發生故障，造成大面積的停電，這嚴重影響了人民的生活并造成了巨大的經濟損失。

2　模型理論

2.1移動平均法

2.1.1基本思想

對于一個時間序列 ｛x2｝，假定在一個比較短的時間間隔里，序列的取值比較穩定，故可以用一段時間間隔內的平均值作為某一期的預測值。在實踐中，m期移動平均法是較為常用的預測方法。假設最后一期的觀察值為xi，那么利用m期移動平均法向前預測第l期的值為：

2.1.2實例分析

根據許昌市統計局2014年各月統計月報數據，利用2012.1-2014.12的社會用電量的月度數據，通過選擇不同的移動平均間隔長度m，對于許昌市社會用電量的月度數據進行計算各自的均方誤差，利用Excel軟件計算各自的均方誤差，當m=3時，SSE=0.9886，當m=4時，SSE=0.9906；當m=6時，SSE=1.2370；當m=12時，SSE=1.4822。由此可知，當取間隔長度為3時，預測值與實際觀測值之間的相對誤差較小，基本都［-10%，10%］范圍內浮動，此時，利用該模型進行短期預測得到的預測精度較高。

2.2時間序列法

2.2.1模型

許多非平穩序列差分后會顯示平穩序列的性質，這時稱這個非平穩序列為差分平穩序列，并對該差分平穩序列可以使用ARINA模型進行擬合.具有如下結構的模型稱為求和自回歸移動平均模型，簡記為ARZNACP，d，q模型：

2.2.2實例分析

取許昌市社會用電量（2012.1-2014.12）的月度時間序列X作為研究對象，首先利用Eviews軟件對其分析，許昌市社會用電量及其殘差序列均呈現線性上升趨勢，而一階差分序列值在［-1，1］范圍內圍繞零上下作隨機波動，由此可知，原觀察值一階差分后平穩.再根據原序列的自相關函數與偏自相關函數圖，可以明顯看出自相關函數和偏自相關函數均2階截尾，故可對該時間序列使用ARIMA（2，1，2）進行擬合.AR（1）、AR（2）的系數均不存在顯著性，因此需要將其剔除后再進行估計。

最終檢驗結果顯示，AR（1）、AR（2）的系數均通過了顯著性檢驗，故對應的模型為ARIMA（0，1，2），其表達式為：DXt=0.1087+εt-0.3284εt-1.-0.6674εt-2其中，輸出結果中0.1087是DXt的均值，表示月平均用電量增量是0.1087億kw·h。

移動平均法、時間序列法的單一模型預測值分別為：2015年1月 （7.50、8.31），2015年2月（7.73、8.41），2015年3月 （7.73、8.51），2015年4月（7.55、8.62），2015年5月（7.63、8.73）。

3　加權組合預測模型

加權組合預測理論認為，對同一個預測問題使用多個不同預測模型的線性組合，在一定條件下可以有效地改善模型的擬合能力和提高預測精度。利用加權組合預測模型進行電力需求預測可以將各個模型有機地組合在一起，綜合各個模型的優點，提供更準確的預測結果。

3.1權重的確定

組合預測法的關鍵在于如何確定組合權重系數，對權重的選擇應使誤差越小越好。當單個單一預測模型的預測精度完全已知時，一般采用加權平均的方法。簡單加權平均法先把各個單一預測模型的預測誤差的方差和進行排序，根據各個單項預測模型的誤差方差和的加權系數成反比可知，排序越在前的單一預測模型，其在組合預測中的加權系數就應越小即：

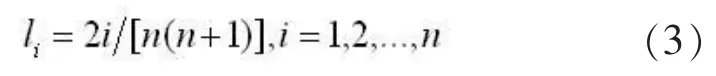
3.2實例分析

3.3模型評價

為了進一步檢驗各模型預測結果的好壞，可以對模型進行進一步的評價：

式中yi為變量觀察值，為變量預測值，m為樣本量.根據上述各評價指標進行預測，得到結果為：移動平均法 （SSE=32.6233，MAE=0.801，MSE=0.1731，MAPE，0.1236），時間序列法（SSE=27.4915，MAE=0.6786，MSE=0.1498，MAPE= 0.1145），簡單加權平均法（SSE=22.2554，MAE= 0.6426，MSE=0.1430，MAPE=0.1016）。

由此可知，加權組合預測法的結果明顯優于單一預測方法，從而說明加權組合預測法的有效性。所以，可以采用簡單加權平均法組合預測模型來對未來幾個月的用電量進行預測，結果為2015年1月為 8.09，2015年 2月為 8.23，2015年 3月為8.29，2015年4月為8.30，2015年5月為8.38。

［1］ 朱琳.電力系統負荷預測方法及其應用［D］.華北電力大學MBA學位論文，2011：1-2.

［2］ Yuanyuan Wang，Jianzhou Wang，Ge Zhao，Yao Dong.Appli cation of residual modification approach in seasonal ARIMA for electricity demand forecasting：A case study of China［J］. Energy Policy48（2012）：284-285.

［3］ 陳旭東，查艷婷.基于GM（1，1）模型對浙江人口的預測［J］.科教導刊.2012（8）：217.

［4］ 黃向陽，金陽等.精算中常用的統計模型［M］.北京：中國人民大學出版社，2009.

［5］ 高鐵梅.計量經濟分析方法與建模：EViews應用及實例（第2版）［M］.北京：清華大學出版社，2009（5）：157.

［6］ 徐國祥.統計預測和決策（第3版）［M］.上海：上海財經大學出版社，2008（11）.

［7］ 戴華娟.組合預測模型及其應用研究［D］.中南大學碩士學位論文，2007（5）：25-26.

［8］ 卓東.組合預測模型研究及其在電力負荷預測中的應用［D］.蘭州商學院碩士學位論文，2007（5）：55-56.

C812