在課堂中探索交流，促進知識生成生長——“勾股定理”教學有感

王　新

（北京市通州區玉橋中學）

在課堂中探索交流，促進知識生成生長——“勾股定理”教學有感

王新

（北京市通州區玉橋中學）

新課程倡導：“數學學習的過程應該是一個探索與交流的過程——在探索的過程中形成自己對數學的理解，并在與他人的交流過程中逐步完善自己的想法。”教師不應是知識的獨裁者，而應是學生探究學習的合作伙伴，教學中要為學生搭建探究、交流的平臺，使知識自然生成、自然生長。筆者以“勾股定理”教學為例，談一下自己在教學中的做法與思考。

一、讓知識在課堂中動態生成

建構主義強調，學習者并不是空著腦袋進入學習情境中的。在日常生活和以往各種形式的學習中，他們已經形成了有關的知識經驗，他們對任何事情都有自己的看法。即使是有些問題他們從來沒有接觸過，沒有現成的經驗可以借鑒，但是當問題呈現在他們面前時，他們還是會基于以往的經驗，依靠他們的認知能力，形成對問題的解釋，提出他們的假設。

教學的核心理念是一切為了每一個學生的發展。這個發展是一個動態的生成過程，就教學知識本身而言只是一個結論，而每個數學知識的發生與發展都是一個動態生成的過程，課堂教學中教師應該精心設計，將這個動態過程展現在學生面前，讓他們親身經歷，經歷知識的發生、發展與形成過程，讓他們真實感受知識的內涵與外延。

如，在“勾股定理”新授課教學中，我并沒有直接將知識結論生硬地搬上課堂，而是首先以學生小時候常做的折紙游戲入手（如圖1），引導學生思考：折疊起的四個等腰直角三角形的邊長與原正方形邊長之間的關系，并不斷變化外部正方形的邊長，使學生在不斷變化的數據中去探究不變的本質特點。與此同時，請同學們動手用圓規和刻度尺畫出直角三角形，使它們的直角邊分別為以下數據（學生分組完成）

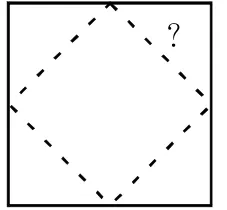
圖1

（1）3厘米，4厘米；（2）6厘米，8厘米；（3）5厘米，12厘米

再次引導學生思考：所做直角三角形的三邊間的數量關系？并通過幾何畫板做演示，使學生在折紙、畫圖、測量、計算的過程中感受知識的合情合理，進而從情感上接受知識。

二、讓課堂成為學生展示的舞臺

教學不是知識的傳遞，而是知識的處理和轉換。教師不單是知識的呈現者，也不應該是知識權威的象征，而應該重視學生自己對各種現象的理解，傾聽他們時下的看法，引導學生豐富或調整自己的解釋。

如，在對勾股定理進行論證的教學環節中，我事先讓學生自學、查詢有關定理的由來與證明方法，做好預習準備工作，并告誡他們上課時我會讓準備充分的學生上臺展示。說實在的，當時只是想讓他們簡單預習一下，沒想到第二天他們在課堂上的表現令我驚訝不已，他們準備之充分、積極性之高是我未曾遇見過的，他們有的做好了教學PPT，有的將證明過程用彩筆寫在了大的掛歷紙上。課堂上，他們各小組討論熱烈；回答問題，積極主動；講臺展示，爭先恐后，表現力極強，其中有些方法既簡單又易理解。

展示如下：

∴a2+2ab+b2=c2+2ab

∴a2+b2=c2

圖2　

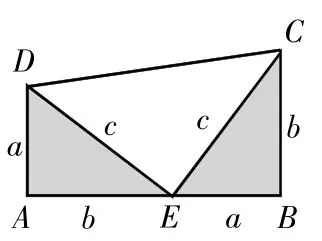
圖3

方法二：以a、b為直角邊，以c為斜邊作了兩個全等的直角三角形，就可以得到每個直角三角形的面積都是把這兩個直角三角形拼成圖中的形狀，使A、E、B三點在一條直線上。利用梯形ABCD的面積等于得到

方法四：如圖5，邊長為c的正方形，由四個全等的直角三角形和一個小正方形組成其面積為c2亦可加以證明。

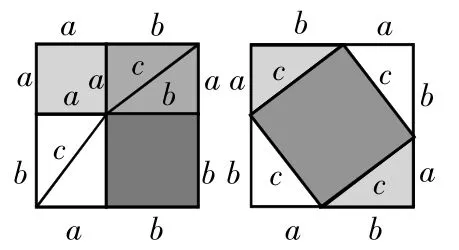
圖4　

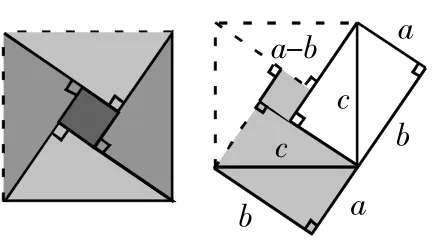
圖5

……

課堂上他們的證法得到認可時的欣喜、自豪的神態至今給我留下了深刻的印象。

我們不可否認，每個學生都是具有豐富思想的個體，他們對知識的接受與理解的途徑和程度也不相同，課堂教學中應盡量讓學生將他們所知、所做、所感、所悟盡情地表達出來，不要用教師的思維代替學生的思維，不要用書本中的語言代替學生的語言，更不能獨占課堂領地。

三、讓課堂成為師生成長的圣地

從古到今，“教學相長”一直是我們所追求的教育境界。所謂“教學相長”，是指“教與學兩方面互相影響和促進，教與學相互依存、相互推動，相輔相成、相得益彰”。這種觀點實質上就是說“課堂應是師生共同成長、提高的場所”。自然界中每一個生命都離不開成長的空間和精心的呵護，教學亦是如此。好的課堂、精彩的課堂應該是活躍的、動態的，是知識與思維之間相互碰撞的，是師生之間、生生之間相互交流、共同探索的過程，是一種生命感染生命、激情點燃激情的過程。

在勾股定理探究學習的過程中，得到提高的不僅是學生，還有我這個具有多年教學經驗的教師，學生的課堂表現進一步沖擊著我的教學觀，他們用實際行動在告訴我“我們才是課堂的主人”“要相信我們能行”。他們的表現督促我要不斷提升自身專業素養，教師的站位決定學生的高度，教師的素養決定學生的素養，正如加德納指出的那樣“每個人都是一個自我完善的過程”，教師也一樣，需要自我完善、自我建構、自我反思、自我提高。教師在學生的成長中發展，學生在教師的發展中成長，我認為這才是真正意義上的教學相長。

因此，教學過程中教師應遵循教育教學規律，認真挖掘教材知識本身的特點，并將其與學生已有的生活經驗相結合，將枯燥的數學知識轉變為探究性問題，讓學生在動手、動腦的探究活動中感受知識的發生與發展，感受作為數學家的成就感、自豪感，感受到數學知識本身獨到的美與魅力，從而變“要我學為我要學”，并在不斷探索、掌握知識的過程中，獲得和提高解決問題的能力。

李道甜.淺談勾股定理的教學與應用［J］.中學教學參考，2010.

·編輯張珍珍