北斗三頻RTK附加中誤差約束的單歷元模糊度固定算法

徐彥田，秘金鐘，鄢中堡，袁宏超，王　鐸

(1. 地理空間信息工程國家測繪地理信息局重點實驗室，北京 100830； 2. 中國測繪科學研究院，北京 100830； 3. 四川省第一測繪工程院，四川 成都 610100)

?

北斗三頻RTK附加中誤差約束的單歷元模糊度固定算法

徐彥田1,2，秘金鐘2，鄢中堡3，袁宏超2，王鐸2

(1. 地理空間信息工程國家測繪地理信息局重點實驗室，北京 100830； 2. 中國測繪科學研究院，北京 100830； 3. 四川省第一測繪工程院，四川 成都 610100)

為了實現北斗三頻RTK單歷元模糊度實時固定，提出了一種附加中誤差約束的TCAR搜索法。該算法用中誤差最小搜索替換TCAR直接取整固定模糊度，即對幾組備選模糊度搜索計算中誤差，其中中誤差最小值組合作為模糊度固定解，按此方法依次固定超寬巷—寬巷—基本頻點模糊度。試驗表明，此方法固定成功率為100%，克服了TCAR直接取整模糊度誤判問題。

北斗；三頻；單歷元；中誤差；模糊度

北斗衛星導航系統具備了亞太區域的導航定位功能，提供三頻觀測信號，可以組合成多種波長較長、噪聲較小的組合觀測值，利于模糊度的實時快速固定，而相位模糊度的固定是實現厘米級RTK動態定位的關鍵。

GNSS三頻觀測值模糊度固定算法研究已有很多，其中RTK短基線三頻模糊度單歷元固定方法最為著名的是TCAR(three carrier ambiguity resolution)法和CIR(cascade integer resolution)方法。這兩種算法原理上是相同的，利用不同偽距和相位組合其波長不同的特點，單顆衛星逐級(超寬巷—寬巷—窄巷)直接取整方式固定模糊度，算法非常簡單，無須搜索，但容易出現模糊度固定錯誤。隨著三頻模糊度解算概念的擴展[1-2]，基于幾何模型的三頻模糊度固定方法發展起來，將位置和模糊度同時作為待估參數求解，計算模糊度浮點解和方差陣，并使用最小二乘降相關搜索法(the least-squares ambiguity decorrelation adjustment methods，LAMBDA)固定模糊度，同樣逐級固定超寬巷—寬巷—窄巷或基本頻點模糊度。LAMBDA方法理論上講是一種數學方法，計算量較大，可靠性較高，但仍存在區間次小和最小方差比值RATIO值大于設定閾值，即出現RATIO大但模糊度錯誤的情況，同樣也會出現RATIO較小但模糊度正確的情況。Teunissen在2002年比較了TCAR、CIR和LAMBDA方法在三頻模糊度解算中的應用，指出TCAR和CIR比較適合無幾何模型的單星模糊度解算，LAMBDA適用于有幾何模型的模糊度固定[3]。

TCAR方法單歷元單星固定三頻模糊度受觀測噪聲影響較大，容易出現模糊度誤判固定錯誤，無法實現模糊度100%固定。為了實現北斗三頻RTK單歷元模糊度固定，本文基于三頻組合觀測值的組合特性選取了幾組合適的超寬巷、寬巷組合觀測值，發現超寬巷或寬巷組合雙差殘差與波長差異明顯，如超寬巷波長4.8 m的組合雙差殘差一般在0.2 m左右，因此模糊度一旦固定錯誤，則引起整周波長倍數的粗差(至少4.8 m)，超寬巷組合觀測值單位權中誤差會出現跳變異常(1周約1 m)；類似的模糊度固定錯誤中誤差異常跳變同樣適用于寬巷和基本頻點觀測值。因此對三頻TCAR方法進行了改進，在固定超寬巷、寬巷和基本頻點模糊度時，附加觀測值單位權中誤差作為模糊度固定的標準。此算法對觀測噪聲較大模糊度直接取整容易出現錯誤的衛星給定2個備選模糊度，而觀測噪聲較小的衛星直接取整固定，從而形成少量備選模糊度向量組合，進而對備選模糊度組合分別判斷觀測值單位權中誤差，其中最小中誤差且中誤差小于設定的閾值時對應的模糊度向量為固定解，逐級(超寬巷—寬巷—窄巷)固定模糊度。通過河北局域實測數據驗證，此方法固定成功率為100%，克服了TCAR中模糊度直接取整誤判問題。

一、三頻觀測值及其線性組合

1. 偽距和相位觀測值

北斗具有3個頻點(B1、B2和B3)觀測值，對于衛星S和接收機R相應的偽距和相位觀測方程可以表示為[4]

Pi=ρ+ctS+ctR+IPi+T+O+εPi

(1)

φi=ρ+λiNi+ctS+ctR+Iφi+T+O+εφi

(2)

式中，P為偽距觀測值；φ為載波相位觀測值；ρ為站星間幾何距離；c為光速，即299 792 458 m/s；tS為衛星鐘差；tR為接收機鐘差；IPi為相應頻率偽距電離層延遲；T為對流層延遲；O為星歷誤差；i為頻點(B1、B2、B3)；εPi為偽距觀測噪聲；λi為波長；Ni為整周模糊度；Iφi為相應頻率相位電離層延遲；εφi為相位觀測噪聲。

2. 最優三頻組合觀測值選取

為了單歷元實現模糊度固定，組合觀測值應該具有更長的波長、更小的噪聲和電離層影響，三頻觀測值可以組合成很多相應的觀測值。根據相關文獻關于三頻組合觀測值的特性的研究[5-8]，三頻觀測值線性組合可以表示為

(3)

組合頻率為

B(i,j,k)=iB1+jB2+kB3

(4)

組合波長為

(5)

組合整周模糊度為

N(i,j,k)=iN1+jN2+kN3

(6)

組合電離層延遲一階放縮因子

(7)

假設3個頻率觀測值等精度，組合觀測噪聲為

(8)

噪聲因子為

(9)

常用的組合觀測值見表1，φ0,1,-1由于具有4.8 m的長波長，稱為超寬巷組合(EWL)，φ1,-1,0、φ1,0,-1波長分別約為0.86和1.02 m，稱為寬巷組合(WL)。本文中采用的寬巷組合波長為0.86 m，B1、B2和B3稱為基本頻點模糊度。

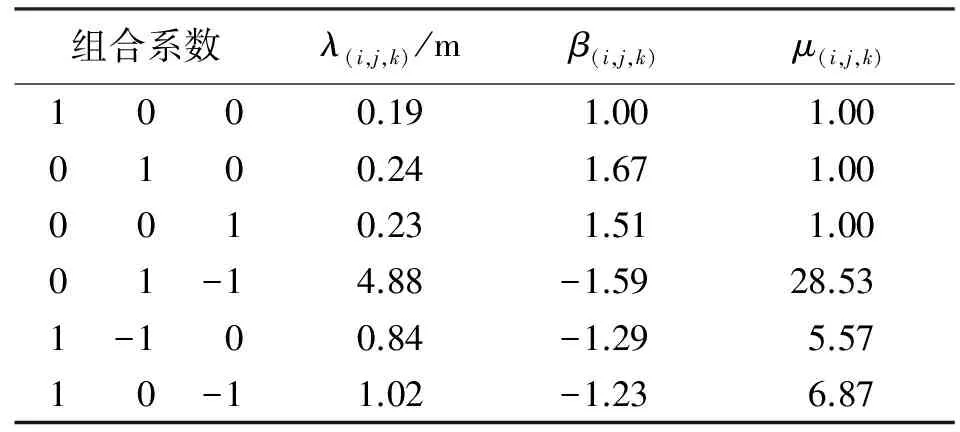
表1　北斗三頻組合觀測值特性

二、模糊度固定錯誤引起中誤差變化分析

觀測值模糊度固定后，觀測殘差主要是差分后大氣延遲殘差和觀測噪聲，一般模糊度固定錯誤造成觀測值出現波長整周倍數的粗差，粗差和正常殘差大小相差懸殊，如超寬巷模糊度粗差一般為4.8 m，正常差分后的殘差為0.2 m左右，最小二乘估計是均方誤差最小的參數估計，粗差與正常殘差的大小懸殊必然引起定位偏差，并直接反映在中誤差上。粗差引起中誤差的變化大小與樣本空間的大小，即衛星個數、模型結構即(衛星圖形)，以及出現粗差的樣本(哪顆衛星)有關。

圖1為2、4號GEO，8號IGSO和12號MEO模擬超寬巷、寬巷和基本頻點模糊度固定錯1周引起的中誤差值變化。從圖中可以看出，粗差與殘差的大小懸殊導致錯誤中誤差與真值差異明顯，且較高衛星與衛星數有關，而較低4號GEO衛星對中誤差影響比較平緩，但與真值差異同樣明顯。總之，模糊度固定錯誤(發生跳周引入粗差時中誤差明顯大于真值)，可以作為模糊度固定參考指標。

三、附加中誤差約束的TCAR搜索法

將式(1)和式(2)組成雙差觀測方程，再相減用于模糊度浮點解計算。常規TCAR方法認為殘差(電離層、觀測噪聲等)對載波影響小于半周，顧及整數特性直接取整獲得固定解。當觀測噪聲和電離層殘差較大時容易出現模糊度固定錯誤，此時本文用TCAR計算的模糊度建立少量備選模糊度組合，前文分析可知模糊度固定錯誤會引起中誤差跳變，因此引入中誤差作為模糊度固定的附加判斷標準，相應的模糊度固定步驟如下：

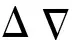
(10)

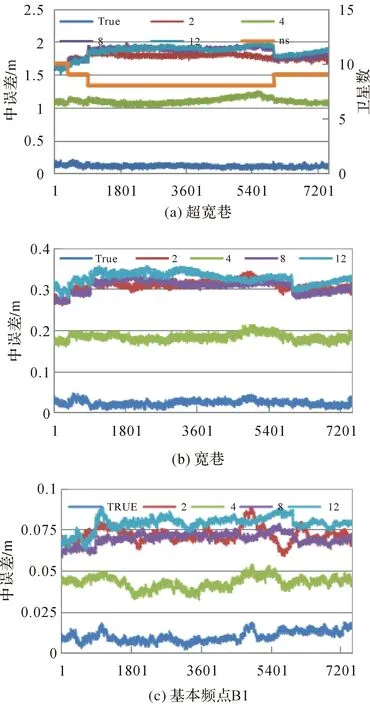
圖1　模糊度錯1周引起的中誤差變化

4) 當前歷元所有衛星通過步驟1)—步驟3)后，建立了備選模糊度向量組合，進而對備選模糊度向量計算中誤差，其中最小且小于設定閾值的中誤差對應的模糊度向量為固定解。

按照步驟1)—步驟4)依次固定超寬巷、寬巷和基本頻點B1模糊度。當固定超寬巷時，P為偽距；固定寬巷時，P為超寬巷；固定B1時，P為寬巷。

四、試驗分析

采用河北區域實際測量數據進行實例分析，采用和芯星通370三頻接收機，觀測時間2015年6月4號中午12：00—14：00，數據采樣率為1 s，基線長度為10.8 km，衛星截止高度角為15°。測站準確坐標用GPS數據靜態解算獲得。

表2統計了常規TCAR方法全部歷元中出現模糊度固定錯誤的衛星情況，寬巷是采用正確超寬巷模糊度下固定錯誤統計、B1是正確寬巷下錯誤統計，顯然三者同時固定錯誤的歷元很少，互不相關。圖2顯示了4號GEO衛星超寬巷、寬巷和基本頻點B1的模糊度浮點解，線條的粗心反映了組合觀測值的組合噪聲大小，當偏差大于0.5周時，直接取整固定錯誤，其中寬巷模糊度37%固定錯誤。

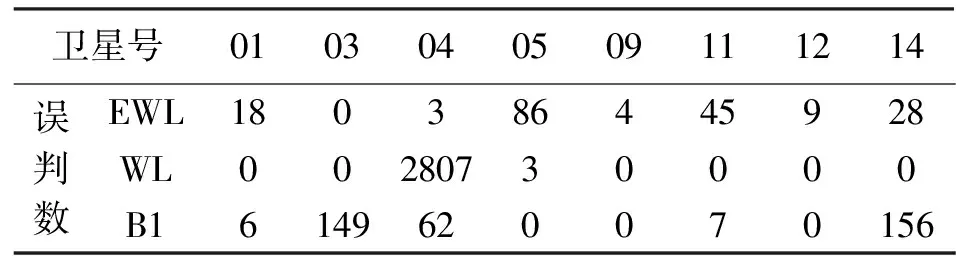
表2　TCAR固定錯誤模糊度統計

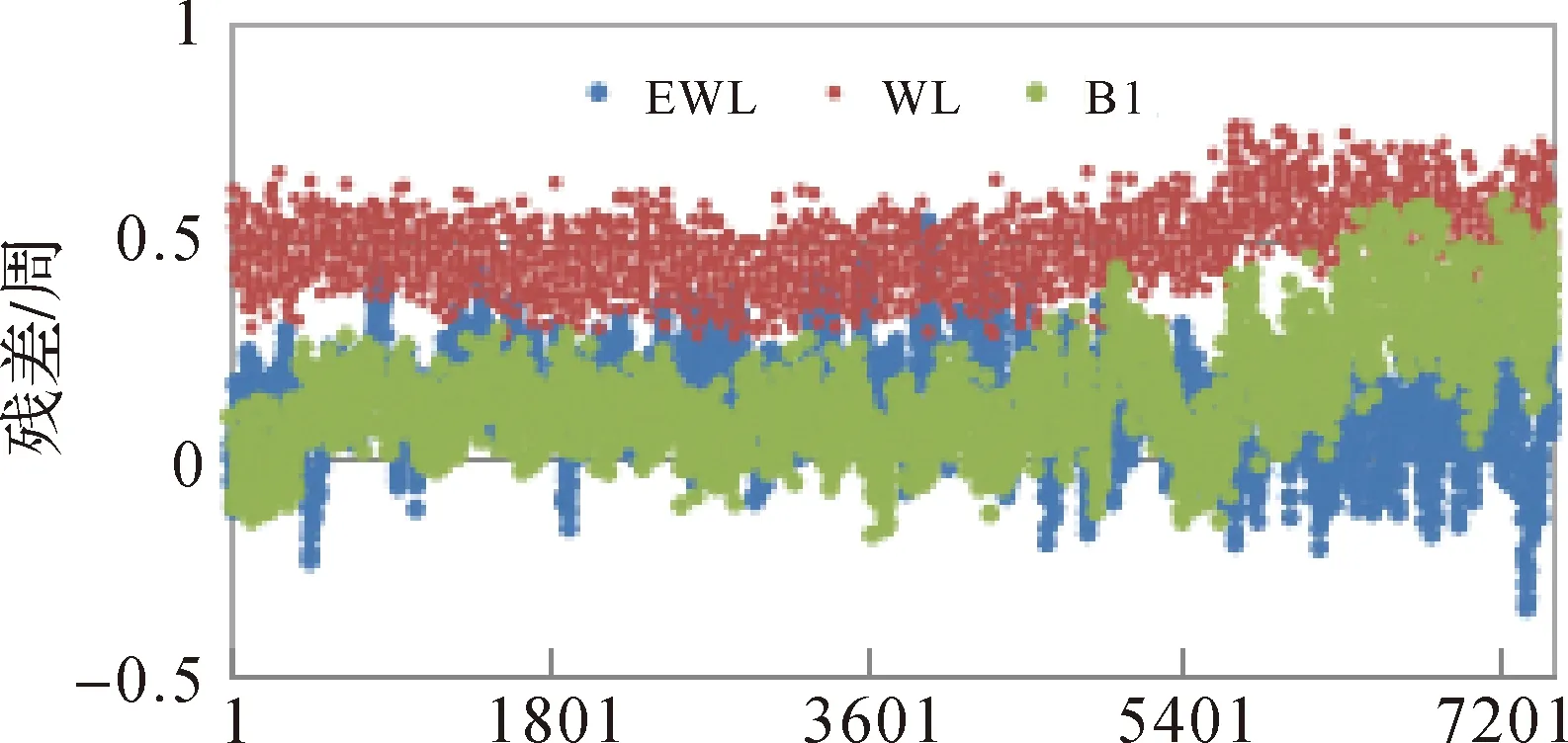
圖2　4號GEO衛星超寬巷、寬巷、B1浮點解

圖3顯示了TCAR方法固定超寬巷、寬巷和基本頻點B1模糊度后相應的觀測值中誤差值。超寬巷模糊度固定錯誤會引起寬巷和B1模糊度固定錯誤，并且超寬巷、寬巷和B1的中誤差大小差不多，明顯大于超寬巷觀測值中誤差數量級；寬巷模糊度固定錯誤同樣引起B1模糊度固定錯誤，并且寬巷與B1的中誤差大小差不多，明顯大于寬巷觀測值中誤差數量級；而B1模糊度固定錯誤時，B1的中誤差明顯大于B1觀測值中誤差數量級。因此模糊度固定正確時，觀測值中誤差明顯小于固定錯誤時，并且差異明顯。

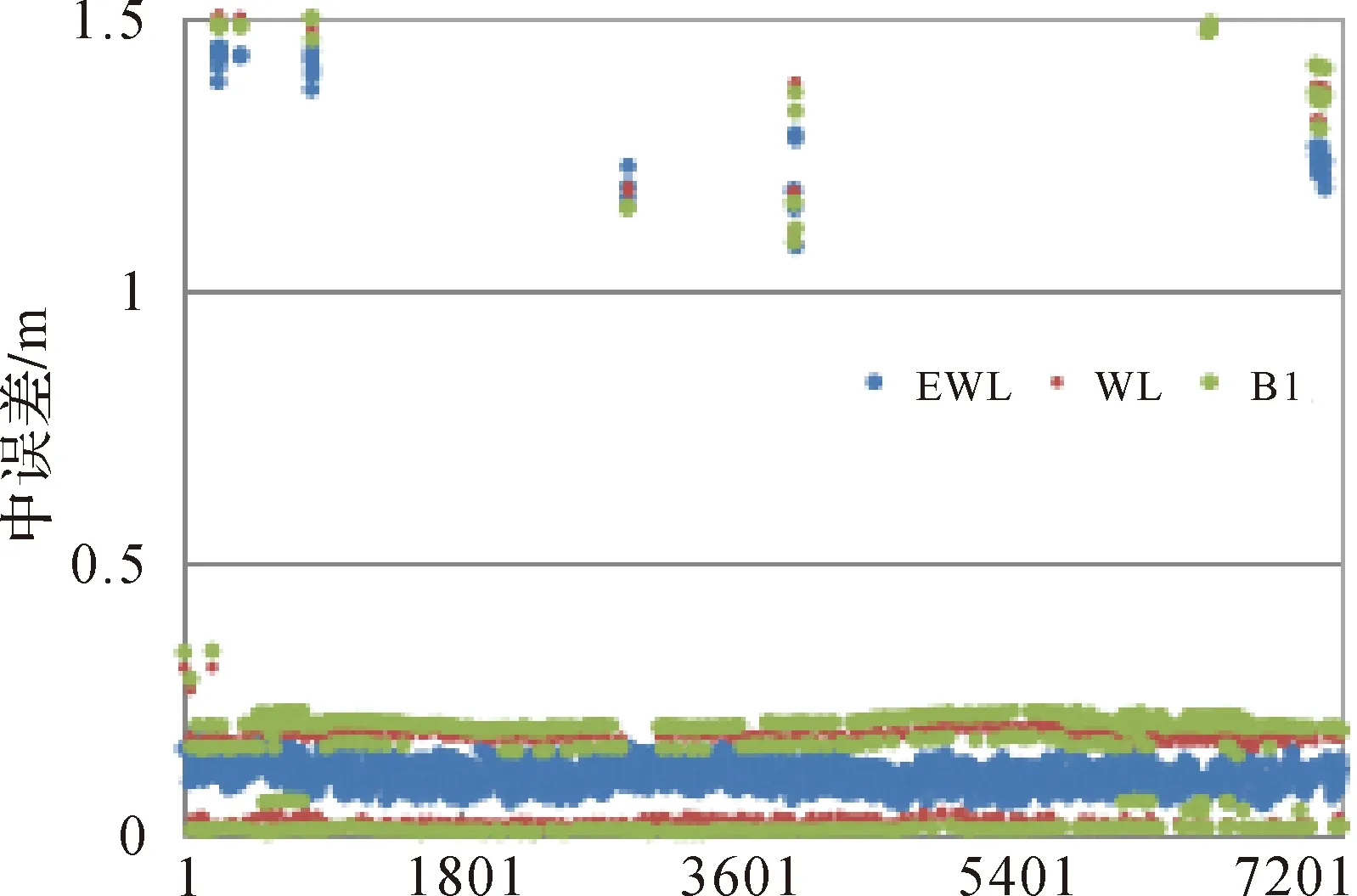
圖3　TCAR方法中誤差

圖4顯示了采用文中所述方法固定模糊度后相應的超寬巷、寬巷和B1頻點觀測值中誤差值，其中沒有較大的跳點值，并且圖5分別顯示了B1使用固定的模糊度的定位偏差值，平面定位偏差優于3 cm，高程優于5 cm。因此附加中誤差約束的TCAR搜索法實現了模糊度100%固定，克服了TCAR直接取整模糊度誤判問題。

圖4　TCAR搜索法的中誤差

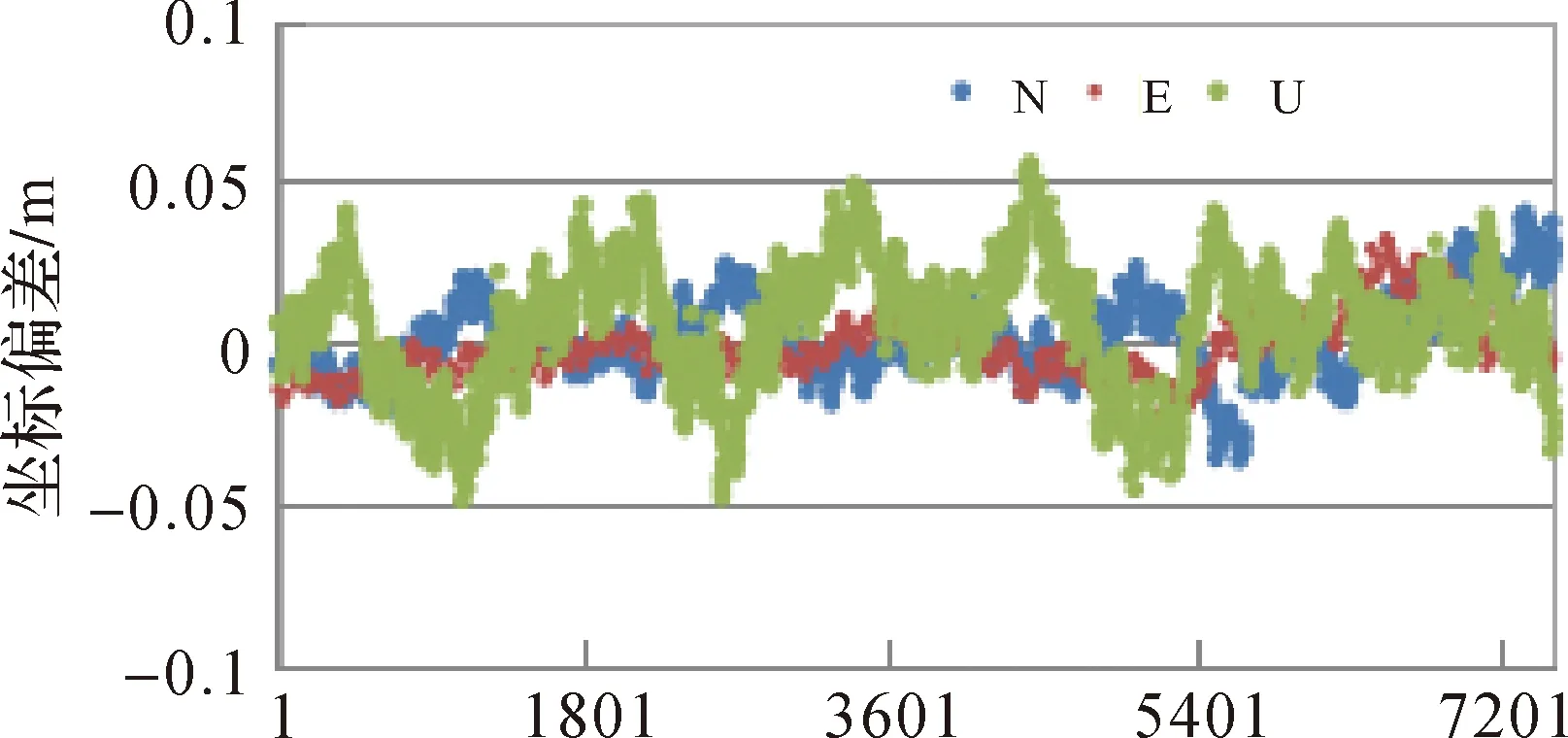
圖5　基本頻點B1定位偏差

五、結束語

本文提出的附加中誤差約束的TCAR搜索法引入觀測值中誤差作為模糊度固定的判斷標準，對TCAR方法建立的少量備選模糊度向量組進行搜索，其中中誤差最小值對應的模糊度向量為固定解，實現了北斗三頻RTK單歷元模糊度實時固定。經實測數據驗證，超寬巷、寬巷和B1模糊度的固定成功率達到100%，克服了常規TCAR方法直接取整的模糊度誤判的弊病，從而實現了三頻單歷元RTK厘米級定位。

[1]范建軍，王飛雪. 一種短基線GNSS的三頻模糊度解算(TCAR)方法[J]. 測繪學報，2007，36(1)：43-49.

[2]劉炎炎，葉世榕，江鵬，等. 基于北斗三頻的短基線單歷元模糊度固定[J]. 武漢大學學報(信息科學版)，2015,40(2)：209-213.

[3]TEUNISSEN P J G, JOOSTEN P. A Comparison of TCAR, CIR and LAMBDA GNSS Ambiguity Resolution[C]∥Proceedings of ION GPS. Portland, Oregon：[s.n.]，2002:2799-2808.

[4]程鵬飛，蔡艷輝，文漢江，等．全球衛星導航系統GPS，GLONASS，Galileo及其他系統[M]．北京：測繪出版社， 2009．

[5]FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J].Journal of Geodesy, 2008(82):847-862.

[6]COCARD M, BOURGON S, KAMALI O, et al. A Systematic Investigation of Optimal Carrier-phase Combinations for Modernized Triple-frequency GPS[J]. Journal of Geodesy ,2008( 82):555-564.

[7]張小紅，何錫揚. 北斗三頻相位觀測值線性組合模型及特性研究[J].中國科學(地球科學)，2015,45(5)：601-610.

[8]黃令勇，宋力杰，王琰，等.北斗三頻無幾何相位組合周跳探測與修復[J].測繪學報，2012，41(5):763-768.

An Algorithm of BDS Three-carrier Ambiguity Resolution with Root Mean Square Error in One Epoch

XU Yantian，BEI Jinzhong，YAN Zhongbao，YUAN Hongchao，WANG Duo

徐彥田，秘金鐘，鄢中堡,等.北斗三頻RTK附加中誤差約束的單歷元模糊度固定算法[J].測繪通報，2016(10)：12-15.DOI:10.13474/j.cnki.11-2246.2016.0319.

2015-12-29

國家863計劃(2015AA124001)；國家測繪地理信息局科技項目(2016KJ0200；2016KJ0205)；四川省測繪地理信息局科技支撐項目(J2015ZC01)；中國測繪科學研究院基本科研業務費(7771503；7771519)；地理空間信息工程國家測繪地理信息局重點實驗室經費(777142108)

徐彥田(1983—)，男，博士，助理研究員，主要研究方向為GNSS高精度定位。E-mail：xuyt@casm.ac.cn

P228

B

0494-0911(2016)10-0012-04