高中數學教學中學生錯誤生成的價值及糾錯策略

◇　江蘇　顏立華

?

高中數學教學中學生錯誤生成的價值及糾錯策略

◇江蘇顏立華

數學是一門嚴謹并且對實踐性要求極高的學科,需要學生不斷去思考,過程中可能會犯下一些錯誤,教師要善于利用這些錯誤，給學生反省的空間,讓學生在反復的實踐中驗證自己的觀點,有意識、有目的整理自己的錯誤,累積經驗,提高自己的準確度,避免重蹈覆轍．

1　正視錯誤,分析價值

學生進入高中階段以后,知識框架與概念已經有了一個基本雛形．但是由于高中數學難度加深等一些客觀原因,還有學生自身的一些主觀原因,很容易犯錯,因此需要學生正視自己的錯誤,多方面的分析錯誤帶來的價值,這樣有利于增加其學好數學的自信心．

1.1數學基礎不牢固,概念不清晰

初中教材上通常將概念條框呈列出來,方便學生更好地理解與掌握,但是高中更注重培養學生自己動腦和動手的能力,需要自己不斷去推理、歸納才能總結出概念,這樣巨大的差距會導致剛進入高中的學生開始跟不上課程,這是高中生容易犯錯的一個重要原因．

AM=N=P;BM?N;

CN?M;DN?P

本題從形式上看，3個集合極為相似，但深入挖掘集合的本質屬性，不難發現它們是不同的集合，集合M是函數y=x2+1中x的取值范圍；集合N是函數y=x2+1中y的取值范圍；P是由函數y=x2+1圖象上的點構成的集合.因此如對集合的概念、性質把握不準，極易出現錯解.

這樣的情況也給教師提供一些有價值的信息: 1)學生基礎不扎實,要自己總結概念分析案例十分困難,或者是概念總結不到位,導致概念理解不清晰,在運用的過程中就容易出錯． 2)教師在課堂教學過程中,沒有有效地指導學生總結概念,在總結重、難點時沒有做到全面.因此教師要進行反省并且思考如何改善自己的教學方案．

1.2綜合性高的組合題，不能融會貫通

在復雜的高中數學學習中,犯錯誤是不可避免的,因為高中數學靈活性強,題型十分廣泛,導致學生在課堂上所學到的不能完全滿足平常的運用,而且高中數學的交會性也十分強,一道題目往往要聯系多個知識點,這樣也會導致學生犯錯．

這道題目不僅考了橢圓的知識,又考了勾股定理的運用,是解析幾何中常見的一種題型．同時也需要學生對知識點理解特別透徹才能運用自如．解題時,若未能徹底掌握此知識點或者運用不熟練,就容易出現錯誤．所以,這類綜合性高的組合題出錯的現象反映了學生融會貫通的能力還有待加強．

2　制定正確的學習方法,預防出錯的指導方針

1) 扎實基礎,梳理概念．

基礎知識的牢固對于數學學習來說是十分重要的,教師應該從高一開始為學生鞏固基本的知識,嚴格要求學生,通過大密度的小測試來檢驗學生對知識的熟悉度．要分析學生概念不清晰的根本原因,不斷調整自己的教學方案,在檢測學生對知識掌握情況的同時分析學生學習困難所在,然后實施相應策略．

r2=|OP|2=a2+(2a)2=5a2.

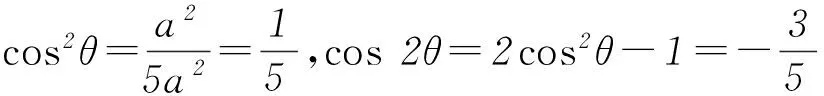
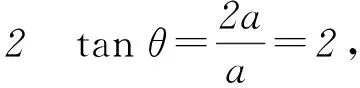
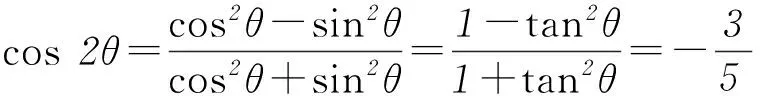
本題只要熟悉三角函數的基本定義就很容易解答出來,所以夯實基礎,牢記概念十分重要．

2) 多加練習,提高正確率,增強學習信心.

教師要想讓學生對數學感興趣,就要根據學生需求的不同制定合適的教學方案,幫助學生制定最佳的學習方案,讓學生自己尋找解題技巧,鼓勵學生上臺到黑板來演練.盡量降低教學的難度,增強學生學習的自信心．比如下面這道例題,是簡單的誘導公式的套用,教師只要嚴格要求學生牢記誘導公式的轉換與“奇變偶不變，符號看象限”的法則，即可求解．

2) 根據上面的判斷方法,運用十字口訣“奇變偶不變,符號看象限”求值.

3) 由點—線—面全面梳理知識點.

高中數學與初中數學最大的區別就在于知識點更廣更多，也更注重思維模式的培養．教師在講課時更注重數學思想和方法的講解,所以學生要學好數學,必須要將學過的知識系統分析、整理,學會舉一反三．高中數學教材每個知識板塊都是有關聯的,教師在教學時要講解全面.例如，學生學習了數列,在理解數列基本概念的同時,還要求學生將函數方程的思想融入其中,這對學生的數學能力要求較高,其中等差數列和等比數列是基礎,僅記憶公式遠遠不夠,比如下面例5．

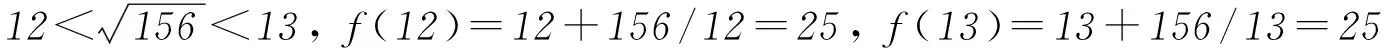
數列是特殊的函數，可從函數角度考慮，利用函數y=f(x)的性質，求數列an=f(n)的最值.

總之,高中數學教師在進行教學時要根據每個錯誤的不同,針對性的制定教學方案,對癥下藥．在發現學生問題的同時,不僅要幫助他們改正錯誤,更重要的是從學生錯誤中總結經驗,善于發現錯誤中所蘊含的價值,才能讓學生更好地掌握解答問題的技巧,提高解題正確率．

江蘇省射陽中學)