一種使用Petri網絡模型驗證協議的方法

蔡俊杰

?

一種使用Petri網絡模型驗證協議的方法

蔡俊杰

隨著計算機網絡的高速發展，開發新型的網絡協議成為熱點研究課題。而新型網絡協議的描述與驗證又成為研究的關鍵。引入Petri網絡模型，給出了一種協議驗證的方法。通過描述Petri網絡模型，該模型以其良好的直觀性，為協議驗證過程提供了極大的方便。并且提出了針對復雜的協議，可分解為若干個小部分，使用Petri模型，加之以有窮狀態自動機和高級語言，可較完善地解決其描述和驗證問題。所述的驗證方法對于協議工程（protocol engineering）領域的研究，新的協議軟件的產生，有著積極的推動作用。

Petri網絡模型；點火；狀態變遷；可達樹

0 引言

當前，網絡技術的發展已經進入了一個全新的時代。OSI參考模型的出現為解決異構系統的互連做出了重要貢獻。但是，由于對OSI協議的開發仍常常由許多不同人員甚至是不同單位的人員進行的。因此，如何系統地開發協議軟件，以確保在不同實現之間能協調地工作，仍是一個十分重要的問題。為了有效地解決這個問題，本文給出了一種使用Petri網絡模型對協議進行驗證的方法。

1 Petri網絡模型定義

Petri網絡模型是一種特殊的自動機模型。它可以用來描述通訊系統中各異步成分之間的關系。這種自動機也是一種變遷模型。它允許同時發生多個狀態的變遷，因此Petri網是一種并發模型。在描述各種協議的過程中時，采用Petri網絡模型是非常方便的，下面介紹Petri網的基本概念，并舉例說明它在描述協議方面的應用。

包（bag）是集合的擴展，和集合相似，包也是某個域中元素的集合。但是在包里，元素可以多次出現。例如：

B1=｛a,b,c｝，B2=｛a｝，B3=｛a,a,a｝，B4=｛a,b,c,c｝，B5=｛c,c,b,b｝。B1和B2就是集合，B3~B5則不是集合。

將元素x在包B中出現的次數記為#（x,B）, 在上述例子中#（a,B1）=1，#（a,B3）=3。

當元素x為包B中的成員時，#（a,B3）=3。

當元素x為包B中成員時，#（x,B）>0。此時可寫為x∈B。包B的基數定義為|B|=。在上述例子中|B5|=4。

域D是一個包中各元素的集合。Dn則是包的空間，它是元素在D中且每個元素出現不超過n次的所有包的集合。例如，當D=｛a,b,c,d｝，則D2=｛｛a,b,c,d｝,{a,a,b,b},{a,a,c,d},…｝。若B∈Dn則對于B：（1）若x∈B，則x∈D；（2）對所有的x，#（x，B）≤n。

集合D∞是域在D中所有包的集合。在每個包中元素出現的次數是沒有限制的。

Petri網的定義

在上述關于包的一些基本概念之基礎上，可以將Petri網定義為一個四元組C=（P，T，I，O），其中：

P=｛p1,p2, …pn｝是位置(place)的有窮集合；

T=｛t1,t2, …,tm｝是變遷的有窮集合，且T與P不相交，即T∩P=φ。

I是輸入函數，是變遷T到位置包的映射，即I：T →P∞。對于每一個tk∈T，可以得出相應的I（tk）={pi,pj, …}。

O是輸入函數，也是一種變遷到位置包的映射，即O：T →P∞。對于每一個對于每一個tj∈T，可以得出相應的O（tk）={pr,ps, …}。

一個Petri網的圖形表示法如圖1所示：

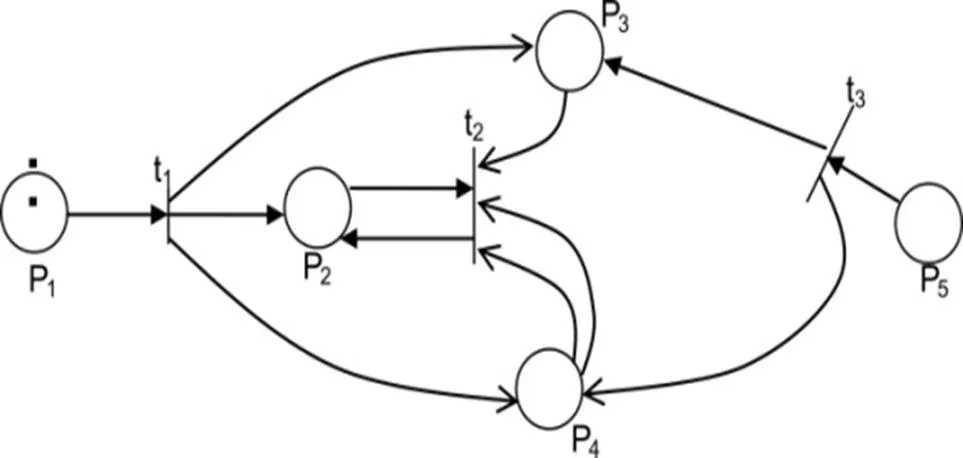
圖1 Petri網的構成舉例

圓圈代表位置。位置又稱為節點或條件。圖1 中的位置共5個。位置集合為P={p1,p2,p3,p4,p5}。短的線段代表變遷。變遷又稱為事件。現在共有3個變遷，變遷集合T=｛t1,t2,t3｝。帶箭頭的直線或弧線指出一個變遷的輸入和輸出位置有哪些。

例如，在圖1中：

I（t1）=｛p1｝,I（t2）=｛p2,p3,p4,p4｝，I（t3）=｛p5｝,

O（t1）={ p2,p3,p4}，O（t2）={p3,p4}。

在Petri網中最值得注意的就是位置圓圈中的黑點，稱之為標記（token）。每一個位置中可以有1個或多個標記，當然也可以沒有標記。Petri網所處的狀態是由標記的分布決定的。在位置pi中的標記個數常用μi來表示。在圖1 中μ1=2，μ2=μ3=μ4=μ5=0。這也可以用向量μ=（μ1，μ2，…μn）來表示整個Petri網的標記分布情況。可以看出，現在μ=（2，0，0，0，0）。

2 Petri網的狀態變遷

一個Petri網的狀態變遷取決于以下兩個條件：

必須有1個或多個變遷滿足變遷條件。變遷條件就是某個變遷ti的所有輸入位置中都必須有標記存在，并且當輸入位置有多根弧線指向這個變遷時，該輸入位置也至少具有和弧線根數相等的標記數。這一條件可寫為公式（1）：

對所有Pi∈I（tj）, μ（pi）≥#(Pi,I(tj)) （1）

對于圖1的例子，只有t1滿足變遷條件。

必須發生點火（firing）。所謂點火就是發生了一些事件（一個或多個），而這些事件所對應的變遷滿足變遷條件。

發生點火后，標記要重新分布。標記移動的規則是：從點火的變遷tj的所有輸入位置中均取出標記，每個位置取出的標記數等于該位置指向點火的tj的弧線數；然后再將標記送入tj的所有輸出位置中去，送入每個位置的標記數等于tj指向該位置的弧線數。顯然，點火前后的標記總數一般是不守恒的。上述規則可用公式表示，設點火標記前標記的分布為μ（pi），則當tj點火后，新的標記分布μ’（pi）可寫為公式（2）：

μ’（pi）=μ（pi）- #（pi,I（tj））+#（pi,O（tj））（2）

可見，對于既非tj的輸入位置又非tj的輸出位置的其它所有位置，其中的標記數在點火前后不發生變化。

仍以圖1的Petri網為例，標記的初始分布為μ=（2，0，0，0，0）。顯然，只有t1滿足變遷條件。當發生使t1點火的事件后，標記的分布變為μ’ =（1，1，1，1，0）。若t1再次點火，則點火后的標記分布為μ’’=（0，2，2，2，0），這時t2已具備點火條件。在t2點火后，新的標記分布變為μ’’’=（0，2，1，0，0）。至此，該Petri網已不能再發生任何點火了。至于實際的應用中，究竟是t1還是t2點火，那就要看具體的條件了。

一個Petri網中的變遷大致有以下3種類型，如圖2所示：

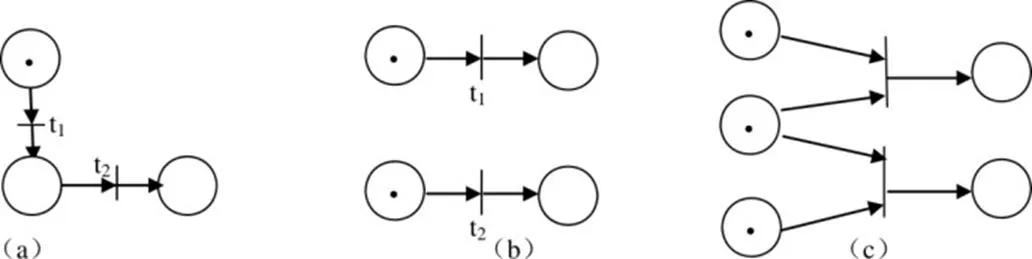
圖2 Petri網中的幾種典型變遷

一種是順序變遷，如圖2（a）所示，只有當t1點火后t2才能點火。另一種是并發變遷，如圖2（b）所示，t1和t2可同時（當然也可以是單獨地）點火。第三種是互斥變遷，如圖2（c）所示，t1和t2中只有一個能點火，一個點火后另一個就不能再點火了。至于在實際中是t1還是t2點火，那就要看具體的條件了。

3 使用Petri網對協議進行描述

下面以甲乙雙方用停止等待協議通信為例，來說明如何使用Petri網對協議進行描述，如圖3所示：

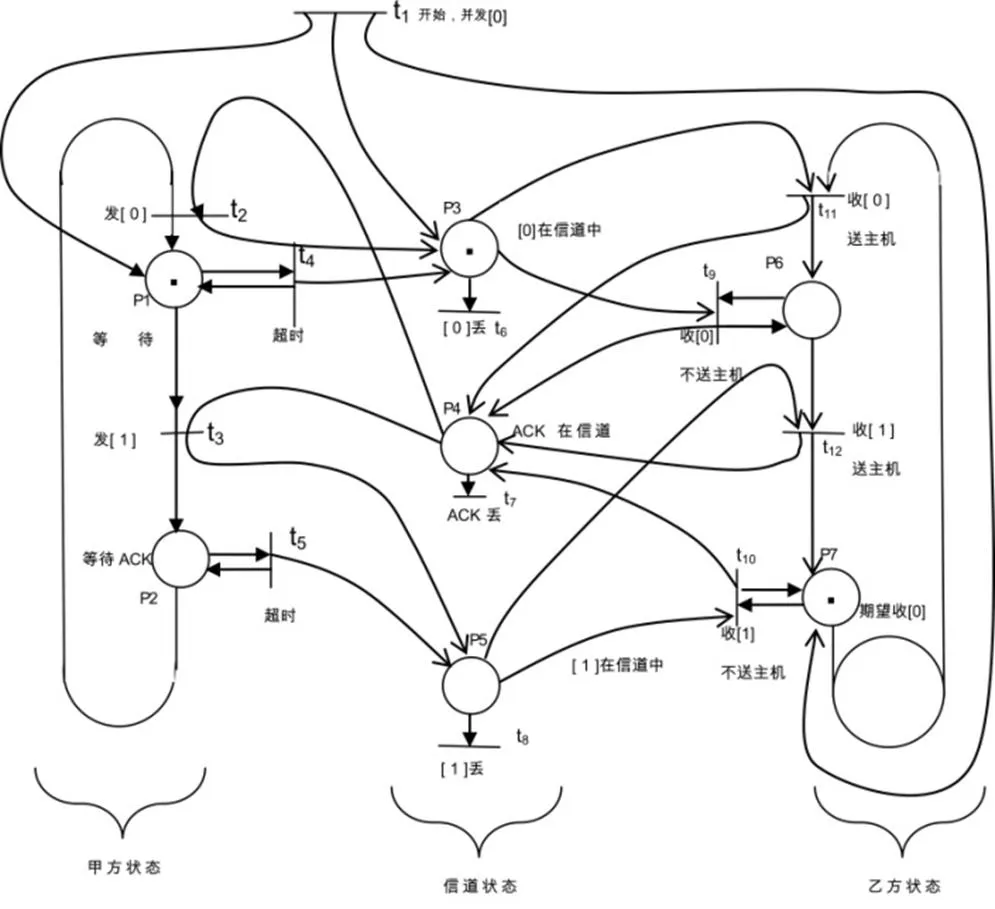
圖3 半雙工通信的停止等待協議的Petri網模型

在圖3中，共有7個位置和12個變遷。開始時，各位置中均無標記，因此，點火只能從t1開始。t1實際上就是整個系統初始化，同時由甲方發出0號幀。t1點火后，位置p1、p3和p7中就各具有一個標記。在這種狀態下，顯然有3個變遷（t4、t6和t11）是滿足變遷條件的。這時究竟哪個變遷點火，則要根據通信的具體情況而定。若0號幀丟失或出錯，則t6點火，p3中的標記即移走（不進入任何位置），這時唯一能夠點火的只有t4（超時）了。整個協議都描述得十分清楚，讀者可依此自行研究每一種變遷在什么條件下方能點火，以及各種狀態的轉換過程。

當然Petri網同樣存在著當協議較復雜時出現過多的位置和變遷，以致很難在圖上將協議描述清楚。但是由于Petri有標記及點火機制，使得Petri網在驗證協議的正確性方面成為很有用的工具。

Petri網模型屬于狀態變遷模型，用這種模型描述協議的最大優點就是直觀性好，同時也便于協議的驗證。

4 使用Petri網對協議進行驗證

使用Petri網不但可以很直觀地對協議進行描述，而且可以對協議進行驗證。具體而言，利用Petri網的可達樹（reachability tree）可以很方便地對協議的若干重要方面進行驗證。

下面以圖3中的協議為例。在一開始t1點火，標記移入位置p1,p3,p7。協議的這種狀態簡稱為（1，3，7）。這相當于以前提到過的標記分布μ=（1,0,1,0,0,0,1）。將狀態（1，3，7）作為可達樹的根，如圖4所示：

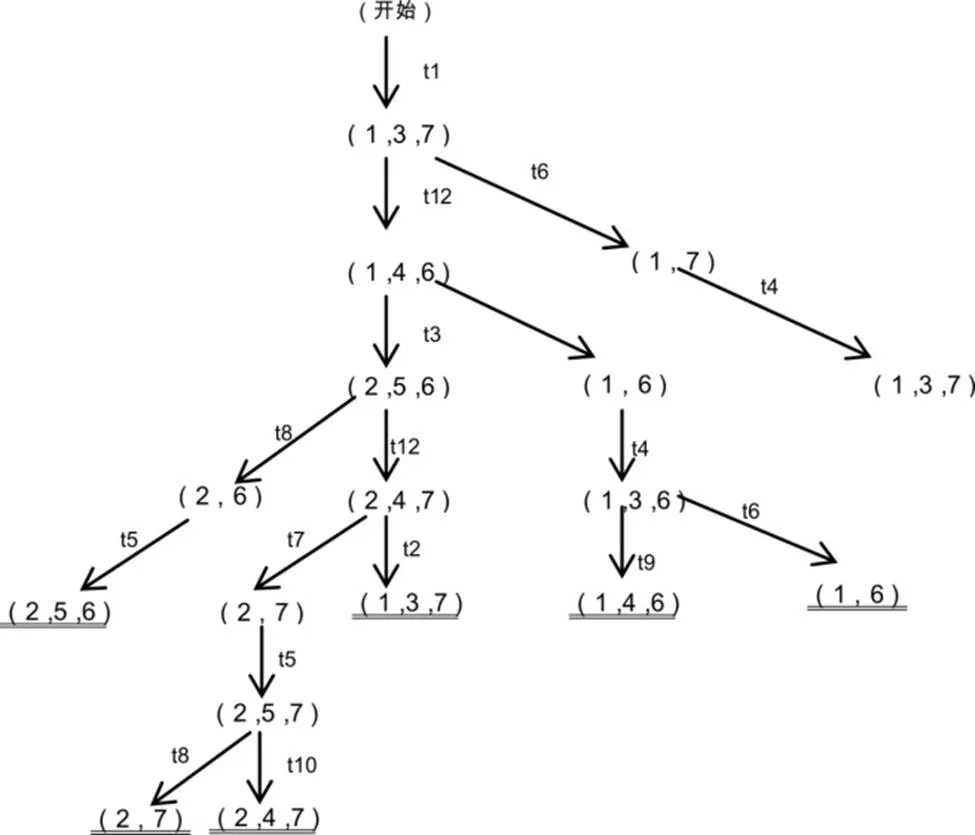
圖4 Petri網的可達樹舉例

再尋找所有滿足條件的變遷。找出當這些變遷點火后所達到的狀態。例如，t11和t6都滿足變遷條件而其余都不滿足變遷條件。若t11點火，則狀態變為(1，4，6，而當t6點火后，標記少了一個狀態為（1，7）。這樣一步一步地進行下去，直到出現一個重復的狀態為止，例如在狀態（1，7）下，t4點火，狀態變為（1，3，7），是個曾經出現過的狀態。于是可在此狀態下劃兩道線，表示不再從該節點上繼續尋找可達樹。

當遍歷所有可能的點火和可能出現的狀態，并且所有的樹葉都成為重復的狀態時，Petri網的可達樹即構成。

從圖4得出的結果可以看出，協議中的所有可能狀態從初始狀態開始都是可達的，還可以看出，由于所有的樹葉都是重復狀態，因此，這樣的協議不可能出現死鎖。從可達樹還可看出，本例也不會出現死循環。

還可檢驗出協議的動作序列都是正確的。例如，甲方從位置1到位置2再回到位置1時，t11和t12均只各點火一次，而且必須點火一次。這就保證了送交主機的幀沒有遺漏，也沒有重復。

大家還可注意到，若單純從圖3來考慮，則只要位置p1（或p2）中有標記，則t4（或t5）在任何時刻均可點火。例如在狀態（1，3，7）時，t1點火后，使狀態變為（1，32，7），這里32表示在位置3中有兩個標記。若t1再次點火，則狀態又變為（1，32，7）。然而根據超時定時器控制原理，剛發出魂的幀還在信道中就接連再重發這個幀是不合理的，因此這種不合理的變遷沒有反映在圖4的可達樹中。但是當t4（或t5）點火時間不受任何限制時，位置3（或5）中的標記數將無限制地增加（因而位置4也會這樣）。這樣的Petri網稱為無界的。與之相對應的是無窮狀態自動機。實際是有用的協議都不會是這樣。

從上述情況可以看出，Petri網許多特性均可以用來進行協議的驗證，但是對于復雜的協議，狀態數目將達到無法進行實驗的程度，些時使用Petri網來解決驗證問題就有困難。大家認為，此時將復雜的協議分解為若干個較小的部分，然后對這些小的部分進行驗證。當協議中包含多個定時器時，要注意這些定時器設定時間的相互協調，盡量避免進程之間信息傳送時間的延時。

總言之，解決協議的驗證問題，應當減少人工的干預，這樣才能使復雜協議的驗證工作大大簡化。

5 總結

網絡協議的研究一直是網絡技術研究的重要課題。本文所描述的Petri網絡模型屬于變遷模型，使用這種模型描述并驗證協議的直觀性好，優點明顯。對于非常復雜的協議的驗證，Petri網絡模型與有窮狀態自動機結合，對于協議的細節，輔之以高級語言來描述，這樣使得協議的描述和驗證均比較方便。本文所闡述的Petri網模型對協議的描述與驗證方法，對于新型網絡協議的研究具有積極的推動作用，具有一定的實用價值。

參考文獻：

[1] 嚴偉,潘愛民(譯)．計算機網絡[M]．清華大學出版社,2012(03)．

[2] 謝希仁．計算機網絡[M]．電子工業出版社,2013(06)．

[3] (美國)科姆．計算機網絡與因特網[M]．清華大學出版社,2010(09)．

[4] 程莉．計算機網絡[M]．科學出版社,2012(04)．

[5] 李成忠．計算機網絡[M]．清華大學出版社,2010(07)．

[6] 段標, 尹曉勇．計算機網絡基礎[M]．電子工業出版社,2012(08)．

[7] 楊琰,廖偉志,李文敬,楊文,李杰．基于Petri網的顧及轉向延誤的最優路徑算法[J]. 計算機工程與設計,2013,34(10): 3643-3648．

[8] 薛晨,任大勇．基于時延Petri網的雙重數字簽名技術研究[J].計算機與數字工程,2013,41(9):1485-1488.

[9] 傅作為樂曉波．基于Petri網的擴展工作流模型研究[J]. 計算機應用與軟件,2013,30(9): 173-175．

[10] 任大勇．基于時延Petri網的移動電子支付協議模型[J].計算機與數字工程,2013,41(10):1622-1624.

Method of Protocol Validation by Using Petri Network Model

Cai Junjie

(Zhaoqing Broadcast Television University, Zhaoqing 526060, China)

With the rapid development of computer networks, the development of new network protocol has become a hot research topic. The description and validation of a new network protocol has become the key of research. This paper introduces the Petri network model, and gives the method of protocol verification. Through the description of the Petri network model, the model provides convenience for protocol verification process with good visibility. And the complex protocols can be decomposed into several small parts. By using the Petri model, it can be a better solution to the problem description and validation combining with the finite state automata and advanced language. Validation of the method presented in this paper for the protocol engineering (Protocol Engineering) research in the field and the new protocol software, has a positive role in promoting.

Petri Network model; Ignition; State Transition; Reachability Tree

1007-757X(2016)04-0078-03

TP393

A

（2015.10.15）

蔡俊杰（1968-），男，安徽人，肇慶廣播電視大學，講師。研究方向：計算機通信、計算機網絡安全、信息安全等，肇慶，526060