黑龍江省灌溉水利用率分形特征與影響因素分析

付　強　劉　巍　劉　東　李天霄　崔　嵩

(東北農業大學水利與建筑學院， 哈爾濱 150030)

?

黑龍江省灌溉水利用率分形特征與影響因素分析

付強劉巍劉東李天霄崔嵩

(東北農業大學水利與建筑學院， 哈爾濱 150030)

黑龍江省不同類型灌區發展不均衡，致使多年來黑龍江省灌溉水利用率普遍低于全國平均水平，為實現黑龍江省灌溉水利用率均衡穩步提升，本文對黑龍江省不同類型灌區灌溉水利用率年度分形特征進行研究，利用位序-規模法對黑龍江省樣點灌區灌溉水利用率的分形特征進行分析，并利用主成分分析法對黑龍江省灌溉水利用率的影響因素進行識別。結果表明：2009—2014年黑龍江省灌溉水利用率年度分維值D在5.26～6.25區間內，且呈現出由多分形向單分形逐步過渡的結構特點，表明黑龍江省不同類型灌區的灌溉水利用率有逐漸趨于均衡分布的態勢；不同類型灌區灌溉水利用率在均衡發展情況下的最大值分別為：大、中型灌區D1=4.58時，η1=44.44%，小型灌區D2=4.79時，η2=53.81%；純井灌區D3=6.98時，η3=70.41%；全省灌區D=5.13時，η=57.03%；渠系襯砌率和灌區工程配套率對大、中型灌區灌溉水利用率的影響程度遠高于其他因素，小型灌區渠系襯砌率影響程度最大，蒸發蒸騰比影響程度最小；田間滲漏量對純井灌區的灌溉水利用率影響程度最大。

灌溉水利用率； 黑龍江省； 分形理論； 位序-規模法； 影響因素； 主成分分析

引言

灌溉水利用率是評價灌區灌溉水利用情況的重要依據，是反映灌區灌溉工程狀況、用水管理水平及灌溉技術水平的重要指標。正確評價灌溉用水效率可為灌區節水灌溉的發展提供科學的理論基礎[1-2]。由于受到人為等因素的影響，使得不同類型灌區灌溉水利用率的發展不均衡，因此，探尋灌溉水利用率的變化趨勢可為不同類型灌區灌溉水利用率的均衡提升提供理論參考[3-5]。

黑龍江省作為我國重要的商品糧基地，多年來其灌溉水利用率均低于全國平均水平[6]。目前黑龍江省有大、中型灌區338個，小型灌區9 136個，純井灌區30萬余個，環境差異及管理方式的不同使得不同類型灌區的灌溉水利用率差異顯著[7-8]。因此,有必要分析黑龍江省不同類型灌區灌溉水利用率的變化規律，并找出制約不同類型灌區的主要影響因素，使得不同類型灌區在其可達到的閾值范圍內得以提升，進而實現黑龍江省灌溉水利用率均衡增長。

目前已有學者對不同類型灌區灌溉水利用率的變化特征展開了研究[9-12]，其中分形理論作為研究事物變化規律復雜性的重要方法之一[13-16]，已逐步被應用到灌溉水利用率的研究中：俞雙恩等[17]利用分形理論研究了河網灌區的分形特征，基于灌溉水利用系數與灌區面積、盒維數的相關性，建立了河網灌區灌溉水利用系數尺度轉換模型；王小軍等[18]利用分形理論中的盒維數法計算了廣東省75個樣點灌區的盒維數，并建立了不同網格尺度下的灌區面積與灌溉水有效利用系數和盒維數空間尺度變異函數；屈忠義等[19]應用 Horton定律計算出河套灌區及灌域的分形維數，并在此基礎上對不同灌域的渠系水利用效率與分維值進行了分析。以往研究對象多為南方灌區，對于北方灌區灌溉水利用率尺度變化規律的研究較少，且研究對象多是某一年的灌溉水利用率，對于省級等較大區域連續多年灌溉水利用率變化特征的研究尚少。因此，本文以我國北方農業大省——黑龍江省為研究對象，將分形理論與位序-規模法相結合對黑龍江省樣點灌區灌溉水利用率的年度分形特點進行研究，同時利用主成分分析法對不同類型灌區的影響因素進行分析，旨為灌區規劃、節水潛力分析等提供科學參考依據。

1　數據與方法

1.1數據來源

選取2009—2014年黑龍江省典型樣點灌區的灌溉水利用率測算值為研究對象。樣點灌區按大、中型灌區(大于667 hm2)、小型灌區(0～667 hm2)和純井灌區分類選取，共選取灌區115個(大、小興安嶺農業分區由于氣候等因素不適于粳稻生長，暫不予以研究)，樣點灌區分布見圖1。灌溉水利用率數據源自2009—2014年黑龍江省灌溉水利用率測算分析結果，影響因素中渠系襯砌率、灌區工程完好率、灌區工程配套率、渠系復雜度、節水灌溉面積比率、田間滲漏量、水田面積比率、蒸發蒸騰比的數據來自黑龍江省灌溉信息網(http:∥www.hljggxx.gov.cn)。各影響因素含意[6-8,18,20]見表1。

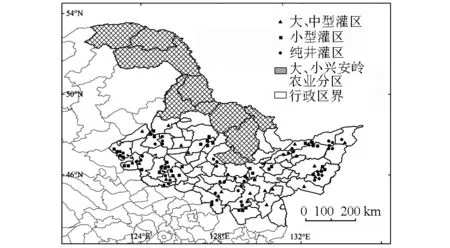
圖1　黑龍江省樣點灌區分布圖Fig.1　Distribution map of irrigation area samples in Heilongjiang province

1.2研究方法

1.2.1位序-規模法

分形是研究事物復雜性客觀變化規律的重要理論，位序-規模法作為研究分形規律的一種方法，由德國學者AUERBACH于1913年首先提出，近些年來，該方法與分形理論相結合，已被廣泛應用于城市結構、城市體系及交通網絡等領域[21-24]。灌溉水利用率受多種可變因素的影響，且各因素對不同類型灌區灌溉水利用率的影響程度不同，使得不同類型灌區灌溉水利用率的層次分布在數理統計角度上呈分維分形的復雜性特征[17-18]，因此，位序-規模法可

表1　灌溉水利用率各影響因素含意Tab.1　Meaning of influence factors for irrigation water use efficiency

注：N為渠道等級數，L為渠道總長度，Lm為主干渠總長度。

被用來研究灌溉水利用率的分形特征[25]。位序-規模法計算公式為

(1)

式中n——樣點灌區數量

Ri——樣點灌區i的位序

Pi——將所有樣點灌區的灌溉水利用率按從高到低排序，位序為i的樣點灌區的灌溉水利用率P1——常數，表示首位序灌區的灌溉水利用率

q——Zipf系數

Zipf系數具有分形性質，與分維值D互為倒數[26]，D可以反映灌溉水利用率分布的均衡趨勢。為了直觀起見，通常對式(1)進行自然對數變換得

lnPi=lnP1-qlnPi

(2)

對式(2)進行線性擬合，擬合直線斜率的絕對值即為Zipf系數，當q>1時，q越大，表明高、低位序灌區的灌溉水利用率差距越大；q=1表示灌溉水利用系數不同區間分布較為均衡(線性分布，即首位序與末位序的灌溉水利用率之比恰為樣點灌區總數)；當q<1時，q越小，高、低位序灌區的灌溉水利用率差距越小[25]。

1.2.2主成分分析

利用主成分分析法對灌溉水利用率的影響因素進行分析。主成分分析(PCA)作為回歸分析的一種，是將多個影響因素轉換為少數相互無關的綜合指標的統計方法，該方法可以很好地處理變量間的多重相關性[27-29]。主成分分析的數學模型為

(i=1,2,…,p;j=1,2,…,k)

(3)

式中Fj——各影響因素的成分

xi——灌溉水利用率的影響因素

aij——因子載荷系數

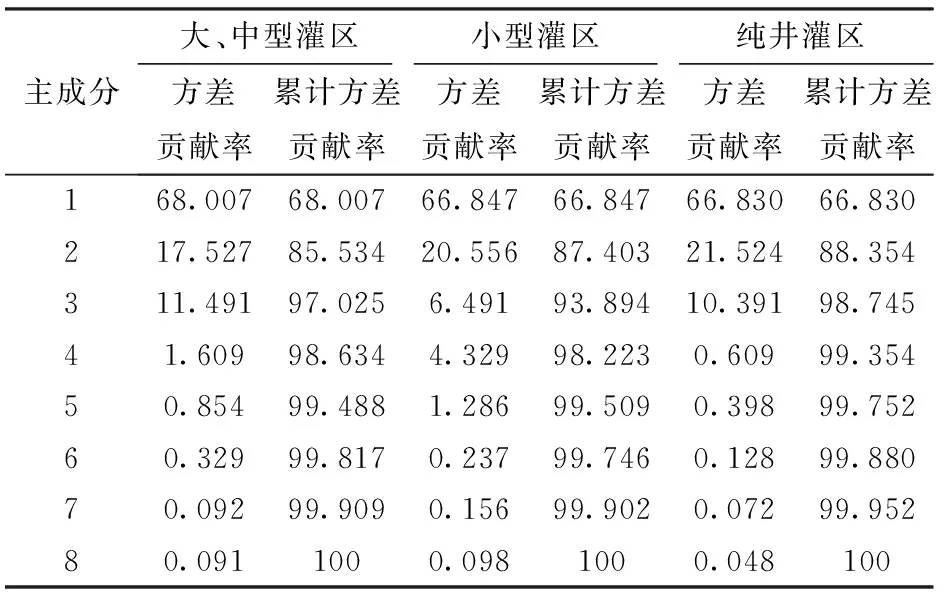
通過計算各主成分的方差貢獻率，選出累計方差貢獻率大于85%的m(m

(4)

式中ωj——第m個主成分的方差貢獻率

Wi——各影響因素的權重，將其歸一化后得到的權重向量即為各影響因素的權重向量W

2　結果分析

2.1灌溉水利用率年度變異分析

根據位序-規模法建立非線性回歸模型(表2)。由表2可知，各年位序-規模表達式的擬合度R2均在0.9以上，表明該方法能較好地描述樣點灌區灌溉水利用率規模分布特征；各年份q均小于1，且呈現逐年增大的趨勢，表明高位序與低位序灌區灌溉水利用率的差距在減小；分維值D在5.26～6.25區間內，整體上呈現減小趨勢，進一步說明灌溉水利用率分布的均衡性逐年增強；灌溉水利用率的理論首位值與實際首位值的比值在1.093～1.196范圍內，表明樣點灌區的首位灌溉水利用率實際發展水平較理想值仍有差距，具有較大發展空間，這為黑龍江省灌溉水利用率的發展提出了更高的要求。

表2　2009—2014年黑龍江省灌溉水利用率規模分布Tab.2　Rank distribution for irrigation water use efficiency in Heilongjiang Province

將2009—2014年樣點灌區的實際灌溉水利用率分別按照從高到低進行排序，繪制樣點灌區的規模位序和對應灌溉水利用率的散點圖(圖2)，通過圖2可以直觀地看出各年度灌溉水利用率的變化特征。從整體上看，黑龍江省灌溉水利用率呈逐年上升的趨勢，但局部變化又有所不同，例如：2011年灌溉水利用率在42%～43%區間內較為突出，低于其他5年；在2013年灌溉水利用率在45%～55%區間高于其他5年，由于各影響因素對不同類型灌區的影響程度不同，造成了灌溉水利用率分布的局部變化，通過以往的研究可知，自然因素對灌溉水利用率的影響并不突出，而灌區管理與工程條件等人為因素是造成灌溉水利用率差異性的主要原因[6]。因此，有必要針對不同類型灌區采取不同措施以提升灌溉水利用率。

圖3　2009—2014年黑龍江省樣點灌區灌溉水利用率位序-規模雙對數變化圖Fig.3　Variation graph of double logarithms of 2009—2014 irrigation water use efficiency rank and size in Heilongjiang Province

圖2　2009—2014年黑龍江省灌溉水利用率位序-規模圖Fig.2　Rank and size distribution graph for 2009—2014 irrigation water use efficiency of Heilongjiang Province

2.2各年度分維特征

分別繪制黑龍江省樣點灌區2009—2014年灌溉水利用率的位數-規模雙對數散點圖(圖3)，并對不同類型樣點灌區進行線性擬合。其擬合直線的斜率與Zipf系數近似相等,其中y為全省樣點灌區擬合直線，y1為大、中型樣點灌區擬合直線，y2為小型樣點灌區擬合直線，y3為純井樣點灌區擬合直線。通過對比6年不同類型樣點灌區的擬合結果可以看出，全省樣點灌區的灌溉水利用率分布均呈現多分形結構；直線y、y1、y2、y3的斜率均逐年增大，這表明，各類型灌區灌溉水利用率分布的均衡性均在逐年增強；其中，直線y3的斜率絕對值變化范圍最大(0.098 0～0.152 5)，y2的斜率絕對值變化范圍最小(0.194 3～0.209 6)，表明純井灌區灌溉水利用率的均衡性提升最為明顯，小型灌區灌溉水利用率分布的均衡性提升最不明顯；直線y3、y2與y的斜率夾角呈現明顯的減小趨勢，而直線y1與y的變化規律并不明顯，但整體上看，黑龍江省灌溉水利用率的分布正從多分形結構逐步向單分形結構發展，表明黑龍江省的灌溉水利用率逐步呈現出均衡增長的趨勢。

2.3分維機制分析

在定性對比的基礎之上，進一步定量分析灌溉水利用率與分維值D的關系。將2009—2014年不同類型灌區灌溉水利用率分布的分維值與灌溉水利用率分別作為橫縱坐標，繪制散點圖(圖4)。從圖4可以看出，不同類型灌區均呈現良好的二次函數關系，通過計算其頂點坐標可以得出不同類型灌區灌溉水利用率分布的分維值D與灌溉水利用率η的最優點(即灌溉水利用率最大，分布均衡性最強)：大、中型灌區分維值D1=4.58時，灌溉水利用率η1最大為44.44%，小型灌區分維值D2=4.79時，灌溉水利用率的η2可達最大值53.81%；純井灌區的分維值D3=6.98時，灌溉水利用率η3可達最大值70.41%；全省灌區分維值D=5.13時，灌溉水利用率η可達最大值57.03%。通過分析分維值與灌溉水利用率的關系，可為減小不同類型灌區灌溉水利用率離散度、均衡提升灌溉水利用率提供理論依據。

圖4　2009—2014年黑龍江省不同類型樣點灌區灌溉水利用率-分維值散點圖Fig.4　Scatter diagram for irrigation water use efficiency and fractal dimension value of different scale irrigation area samples in 2009—2014

2.4影響因素分析

為有針對性地提升不同類型灌區的灌溉水利用率，使全省灌溉水利用率實現穩步均衡增長，對不同類型灌區灌溉水利用率的影響因素進行分析。由于各變量之間可能存在線性關系，因此，采用主成分分析法對影響黑龍江省不同類型灌區灌溉水利用率的因素進行分析。影響因素包括：渠系襯砌率x1、灌區工程完好率x2、灌區工程配套率x3、渠系結構復雜度x4、節水灌溉面積比率x5、田間滲漏量x6、水田面積比率x7、蒸發蒸騰比x8。

通過SPSS軟件，得出各主成分的特征值及方差貢獻率(表3)，可以看出3種類型樣點灌區的第1、2主成分的累計方差貢獻率均在85%以上，表明前2個成分已包含了各影響因素中的大部分信息，因此，3種類型樣點灌區均選用主成分1、2即可。表4為不同類型樣點灌區各主成分的因子載荷系數。

表3　各主成分方差貢獻率Tab.3　Variance conturbution rate of principal component analysis　%

表4　主成分因子載荷系數Tab.4　Factor loading coefficient of principal component analysis

圖5　不同類型灌區各影響因素權重分布圖Fig.5　Influence factors weights of different scales irrigation area

根據式(4)計算出不同類型灌區各影響因素的權重，結果見圖5。可以看渠系襯砌率和灌區工程配套率對大、中型灌區的影響程度遠高于其他6項因素，這表明對于大、中型灌區而言，應減少輸水過程中的滲漏損失，且黑龍江省的大、中型灌區大多建設年代較遠，灌溉工程設備更新緩慢，應當加強大、中型灌區工程基礎設施的配套建設；對于小型灌區而言，影響程度最大的因素為渠系襯砌率，其次為灌區工程配套率、灌區工程完好率與田間滲漏量，蒸發蒸騰比的影響程度最小，且遠低于其他指標，表明對于小型灌區仍應加強基礎工程的建設與養護工作；灌溉工程配套率、節水灌溉面積比率和田間滲漏量這3個因素對純井灌區的影響遠高于其他影響因素，其中，田間滲漏量對純井灌區的灌溉水利用率影響程度最大，因此，對于純井灌區而言，提高灌溉水利用率的關鍵在于減少田間滲漏[20,30]。

3　結論

(1)黑龍江省樣點灌區灌溉水利用率分布符合位序規模-分布法則，2009—2014年灌溉水利用率的理論首位值與實際首位值的比值范圍在1.093～1.196區間內，表明樣點灌區的理論灌溉水利用率較實際水平仍然存在較大差距；2009—2014年樣點灌區灌溉水利用率的分維值范圍在5.26～6.25區間內，且呈現逐年減小的趨勢，表明黑龍江省灌溉水利用率分布的均衡性逐年增強。

(2)大、中型灌區、小型灌區和純井灌區的灌溉水利用率分布的均衡性均逐年增強，其中，純井灌區灌溉水利用率分布的均衡性提升最為明顯，而小型灌區均衡性提升范圍最小；整體上看，黑龍江省灌溉水利用率的分布逐步從多分形結構向單分形結構轉變。

(3)大、中型灌區分維值D1=4.58時，灌溉水利用率達最大值44.44%，小型灌區分維值D2=4.79時，灌溉水利用率可達最大值53.81%；純井灌區的分維值D3=6.98時，灌溉水利用率可達最大值70.41%；全省灌區D=5.13時，灌溉水利用率可達最大值57.03%。

(4)大、中型灌區灌溉水利用率的主要影響因素為渠系襯砌率和灌區工程配套率；小型灌區影響程度最大的因素為渠系襯砌率，蒸發蒸騰比的影響程度最小；純井灌區的主要影響因素為田間滲漏量。

1SAMUEL M P, MATHEW A C. Improving water use efficiency by integrating fish culture and irrigation in coconut based farming system: a case study in Kasaragod district of Kerala (India)[J]. International Journal of Agricultural & Biological Engineering, 2014，7(2)：36-44.

2崔遠來，熊佳. 灌溉水利用效率指標研究進展[J]. 水科學進展，2009，20(4)：590-598.

CUI Yuanlai, XIONG Jia. Advances in assessment indicators of irrigation water use efficiency[J]. Advances in Water Science, 2009, 20(4):590-598.(in Chinese)

3陳皓銳，伍靖偉，黃介生，等. 關于灌溉用水效率尺度問題的探討[J]. 灌溉排水學報，2013，32(6)：1-6.

CHEN Haorui, WU Jingwei, HUANG Jiesheng, et al. Discussion about several scale issues of irrigation water use efficiency[J]. Journal of Irrigation and Drainage, 2013, 32(6):1-6.(in Chinese)

4崔遠來，董斌，李遠華，等. 農業灌溉節水評價指標與尺度問題[J]. 農業工程學報，2007，23(7)：1-7.

CUI Yuanlai, DONG Bin, LI Yuanhua, et al. Assessment indicators and scales of water saving in agricultural irrigation[J]. Transactions of the CSAE, 2007, 23(7):1-7.(in Chinese)

5陳皓銳，黃介生，伍靖偉，等. 灌溉用水效率尺度效應研究評述[J]. 水科學進展，2011，22(6)：872-880.

CHEN Haorui, HUANG Jiesheng, WU Jingwei, et al. Review of scale effect on the irrigation water use efficiency[J]. Advances in Water Science, 2011, 22(6):872-880.(in Chinese)

6付強，劉巍，劉東，等. 黑龍江省灌溉用水效率指標體系空間格局研究[J]. 農業機械學報，2015，46(12)：127-132.

FU Qiang, LIU Wei, LIU Dong, et al. Spatial distribution of irrigation water use efficiency index system in Heilongjiang province[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12):127-132.(in Chinese)

7王小軍，張強. 廣東省灌溉水有效利用系數影響因素的動靜態分析[J]. 水利水電科技進展，2015，35(2)：6-11.

WANG Xiaojun, ZHANG Qiang. Static and dynamic analysis of factors affecting the efficient utilization coefficient of irrigation water in Guangdong province[J]. Advances in Science and Technology of Water Resources, 2015, 35(2):6-11.(in Chinese)

8譚芳，崔遠來，王建漳. 灌溉水利用率影響因素的主成分分析——以漳河灌區為例[J]. 中國農村水利水電，2009(2)：70-73.

TAN Fang, CUI Yuanlai, WANG Jianzhang. Impact factors of irrigation water use efficiency based on principal component analysis, case from Zhanghe irrigation district[J]. China Rural Water and Hydropower, 2009(2):70-73.(in Chinese)

9謝先紅，崔遠來. 灌溉水利用效率隨尺度變化規律分布式模擬[J]. 水科學進展，2010，21(5)：681-689.

XIE Xianhong, CUI Yuanlai. Distributed hydrological modeling of irrigation water use efficiency at different spatial scales[J]. Advances in Water Science, 2010, 21(5):681-689.(in Chinese)

10代俊峰，崔遠來. 基于SWAT的灌區分布式水文模型——Ⅱ.模型應用[J]. 水利學報，2009，40(3)：311-318.

DAI Junfeng, CUI Yuanlai. Distributed hydrological model for irrigation area based on SWAT Ⅱ. model application[J]. Journal of Hydraulic Engineering, 2009, 40(3):311-318.(in Chinese)

11操信春，吳普特，王玉寶，等. 不同灌溉水分生產率指標的時空變異與相關關系[J]. 農業機械學報，2014，45(4)：189-194.CAO Xinchun, WU Pute, WANG Yubao, et al. Spatial and temporal variation of three irrigation water productivity indexes in China[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(4):189-194.(in Chinese)

12SINGH R, VAN DAM J C, FEDDES R A. Water productivity analysis of irrigated crops in Sirsa district, India[J]. Agricultural Water Management, 2006, 82(3): 253-278.

13秦耀辰，劉凱. 分形理論在地理學中的應用研究進展[J]. 地理科學進展，2003，22(4)：426-436.

QIN Yaochen, LIU Kai. Advancement of applied studies of fractal theory in geography[J]. Progress in Geography, 2003, 22(4):426-436.(in Chinese)

14張少文，王文圣，丁晶，等. 分形理論在水文水資源中的應用[J]. 水科學進展, 2005,16(1)：141-146.

ZHANG Shaowen, WANG Wensheng, DING Jing, et al. Application of fractal theory to hydrology and water resources[J]. Advances in Water Science , 2005, 16(1):141-146.(in Chinese)

15WHARTON G, TOMLINSON J J. Flood discharge estimation from river channel dimensions: results of applications in Java, Burundi, Ghana and Tanzania[J]. Hydrological Sciences Journal, 1999, 44(1):97-111.

16劉德平. 分形理論在水文過程形態特征分析中的應用[J]. 水利學報，1998，29(2)：21-26.

LIU Deping. The application of fractal theory in hydrologic process shape characteristic analysis[J]. Journal of Hydraulic Engineering, 1998,29(2): 21-26.(in Chinese)

17俞雙恩，于智恒，郭杰，等. 河網區灌溉水利用系數的尺度轉換[J]. 農業工程學報，2015，31(8)：147-151.

YU Shuang’en, YU Zhiheng, GUO Jie, et al. Scale transformation of utilization coefficient of irrigation water in riverine irrigation district[J]. Transactions of the CSAE, 2015, 31(8):147-151.(in Chinese)

18王小軍，張強，古璇清. 基于分形理論的灌溉水有效利用系數空間尺度變異[J]. 地理學報，2012，67(9)：1201-1212.

WANG Xiaojun, ZHANG Qiang, GU Xuanqing. Fractal-based effective utilization coefficient of irrigation water space scale variability[J]. Acta Geographica Sinica, 2012, 67(9):1201-1212.(in Chinese)

19屈忠義，楊曉，黃永江，等. 基于Horton分形的河套灌區渠系水利用效率分析[J]. 農業工程學報，2015，31(13)：120-127.

QU Zhongyi, YANG Xiao, HUANG Yongjiang, et al. Analysis of efficiency of water utilization in canal-system in Hetao irrigation district based on Horton fractal[J]. Transactions of the CSAE, 2015, 31(13):120-127.(in Chinese)

20閆昕. 黑河中游灌區不同尺度灌溉水有效利用系數估算[D]. 北京：中國水利水電科學研究院，2015.

21DAS R J, DUTT A K. Rank-size distribution and primate city characteristics in India—a temporal analysis[J]. GeoJournal, 1993, 29(2):125-137.

22程開明，莊燕杰. 城市體系位序-規模特征的空間計量分析——以中部地區地級以上城市為例[J]. 地理科學，2012，32(8)：905-912.

CHENG Kaiming, ZHUANG Yanjie. Spatial econometric analysis of the rank-size rule for urban system: a case of prefectural-level cities in China’s middle area[J]. Scientia Geographica Sinca, 2012, 32(8):905-912.

23楊國良，張捷，劉波，等. 旅游流流量位序-規模分布變化及其機理——以四川省為例[J]. 地理研究，2007，26(4)：662-672.

YANG Guoliang, ZHANG Jie, LIU Bo, et al. Study on tourists flow rank-size distribution variation and the mechanism: taking Sichuan province as an example[J]. Geographical Research, 2007, 26(4):662-672.(in Chinese)

24趙媛，牛海玲，楊足膺. 我國石油資源流流量位序-規模分布特征變化[J]. 地理研究，2010，29(12)：2121-2131.

ZHAO Yuan, NIU Hailing, YANG Zuying. Study on the rank-size distribution and variation of crude oil flow in China[J]. Geographical Research, 2010, 29(12):2121-2131.(in Chinese)

25王小軍，張強，易小兵. 廣東省灌溉水有效利用系數年度變化與影響因素關系分析[J]. 灌溉排水學報，2015，34(1)：64-68.

WANG Xiaojun, ZHANG Qiang, YI Xiaobing. Annual variation of irrigation water effective utilization coefficient and analysis of influencing factors in Guangdong province[J]. Journal of Irrigation and Drainage, 2015, 34(1):64-68.(in Chinese)

26FRAGKIAS M, SETO K C. Evolving rank-size distributions of intra-metropolitan urban clusters in South China[J]. Computers, Environment and Urban Systems, 2009, 33(3):189-199.

27李浩鑫，邵東國，尹希，等. 基于主成分分析和Copula函數的灌溉用水效率評價方法[J]. 農業工程學報，2015，31(11)：96-102.

LI Haoxin, SHAO Dongguo, YIN Xi, et al. Evaluation method for irrigation-water use efficiency based on principle component analysis and Copula function[J]. Transactions of the CSAE, 2015, 31(11):96-102.(in Chinese)

28李世華，牛錚，路鵬，等. 基于主成分分析紅壤有效含水量估算模型[J]. 農業工程學報，2007，23(5)：92-94.

LI Shihua, NIU Zheng, LU Peng, et al. Red soil available water capacity statistical model based on principal component analysis[J]. Transactions of the CSAE, 2007, 23(5):92-94.(in Chinese)

29JOLIFFE I T, MORGAN B J. Principal component analysis and exploratory factor analysis[J]. Statistical Methods in Medical Research, 1992, 1(1):69-95.

30馮保清. 我國不同尺度灌溉用水效率評價與管理研究[D]. 北京：中國水利水電科學研究院，2013.

Fractal Characteristics and Influence Factors Analysis of Irrigation Water Use Efficiency in Heilongjiang Province

Fu QiangLiu WeiLiu DongLi TianxiaoCui Song

(CollegeofWaterConservancyandArchitecture,NortheastAgriculturalUniversity,Harbin150030,China)

In order to investigate the fractal characteristics and influence factors of irrigation water use efficiency in different scales irrigation areas, the measuring results of irrigation water use efficiency in 115 different scales irrigation area were selected as samples during 2009—2014. The fractal characteristics of above samples were studied by using the method of rank-size distribution, and the influence factors of irrigation water use efficiency of Heilongjiang province were analyzed by using principal component analysis. The result showed that the fractal dimension valueDof irrigation water use efficiency of Heilongjiang province was ranged in 5.26～6.25 in 2009—2014, and the distribution of irrigation water use efficiency changed from multi-fractal structure to single fractal structure. For the large-middle scale irrigation area (D1=4.58), irrigation water use efficiency was the maximum of 44.44%. For the miniature irrigation area (D2=4.79), irrigation water use efficiency was the maximum of 53.81%. For the pure well irrigation area (D3=6.98), irrigation water use efficiency can reach maximum of 70.41%. For the whole province (D=5.13), irrigation water use efficiency can reach maximum value of 57.03%. In the influence factors analysis for irrigation water use efficiency of different scales irrigation area, the channel lining rate and engineering equipment rate were the most two influential factors to irrigation water use efficiency of large-middle scale irrigation area. To miniature irrigation area, the influence of the channel lining rate was the most, and the influence of the ratio of evaporation to transpiration was the least. Field leakage was the most influential factor to irrigation water use efficiency of pure well irrigation area. The research results provided a theoretical basis for the balanced promotion of irrigation water use efficiency in Heilongjiang province.

irrigation water use efficiency； Heilongjiang province； fractal theory； rank-size method； influence factor； principal component analysis

10.6041/j.issn.1000-1298.2016.09.022

2016-03-12

2016-04-06

國家自然科學基金項目(51479032、51279031、51579044)、黑龍江省高校長江學者后備支持計劃項目和黑龍江省水利廳科技項目(201318、201503)

付強(1973—)，男，教授，博士生導師，主要從事農業水土資源系統分析研究，E-mail：fuqiang0629@126.com

S274

A

1000-1298(2016)09-0147-07