一種混合模型的閉環辨識方法
一種混合模型的閉環辨識方法

過程模型是實施先進控制的基礎,基于系統的開環響應,進行過程模型辨識,是常用的辨識方法。因為開環系統只需持續激勵,總是可辨識的。開環系統的輸入信號與輸出噪聲不相關,經典的辨識方法可獲得對象的一致無偏估計。
但出于生產安全或產品質量的考慮,很多工業過程不允許開環測試。閉環系統由于反饋的存在,噪聲信息引入了系統,系統的輸入輸出具有相關性,常規的開環辨識方法結果往往是有偏的,甚至會導致模型不可辨識。針對這類問題,一些新算法相繼提出,其中基于Box-Jenkins模型(B-J)的算法是一類應用較廣的算法,B-J模型是一種過程模型和噪聲模型相結合的參數模型,是解決包含有色噪聲的辨識問題的一種有效方法。辨識混合B-J模型的有效方法之一是輔助變量(instrumental variable,IV)算法,它不但對低維對象有很好的辨識效果,對于高維的復雜過程以及包含有色噪聲及非線性和時變類型的對象同樣具有優勢。
為實現基于工業生產運行數據而不進行測試進行閉環回路辨識,本文提出了一種基于混合Box-Jenkins模型和IV算法的閉環模型辨識算法。
閉環控制系統結構
工業控制系統的拉普拉斯域(s 域)閉環控制回路結構如圖1所示,圖中r (s)為回路的設定值,Gc(s)為控制器,u(s)為控制器輸出,Gm(s)為過程模型,Gn(s)為干擾通道的傳遞函數,ξ(s )為有色噪聲,w(s)為均值0方差σ2的高斯白噪聲,y (s)為系統輸出,式中的s 為拉普拉斯算子。
由經典控制理論可知,圖1所示的工業對象可表示為線性穩定的單輸入單輸出系統,系統可由以下公式來描述:

圖1 閉環控制回路結構圖

過程模型Gm(s)定義為:

式中ai, i=1,L ,na和bi, i=0,L ,nb為模型參數,nb和na分別為傳遞函數的分子與分母的階次且na≥nb。
s 域所對應的時域過程模型可表示為:

這里Gm(p)為過程模型Gm(s)的對應時域模型,p 為對應的時域算子。
為計算的方便性,而不涉及到過多的理論推導,干擾模型Gn(s)以ARMA模型表示,所對應的時域傳遞函數為:

式中z-1為后移算法子,滿足z-1ξ(k)=ξ(k-1),di, i=1,L ,nd和ci, i=0,L ,nc為模型參數系數,nd和nc分別為噪聲模型Gn的分子與分母階次。這一模型可以使用基于IV算法的IVARAM算法進行辨識。
另外時域控制器模型表示為:
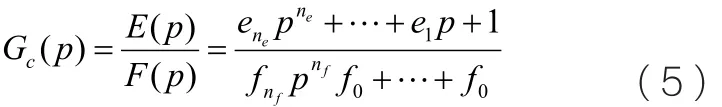
式中ei, i=1,L ,ne和fi, i=0,L ,nf為控制器參數系數,ne和nf分別為控制器模型Gc的分子與分母階次。
基于輔助變量的混合B-J模型辨識
為解閉環回路中輸入輸出中因反饋噪聲的存在造成過程模型辨識的有偏性問題,Young等提出了基于輔助變量的混合B-J模型辨識(CLRIVC)算法。算法通過定義一個新的預濾波器,解決了連續時間辨識輸入輸出數據的求導問題。算法基以y( tk)和計算得到的u( tk)的預濾波數據建立過程向量;基于公式(15)?計算不含循環噪聲成份的x(tk)和v(tk),以x(tk)和v(tk)的預濾波數據建立輔助向量,應用公式(18)迭代求混合B-J模型。預濾波器具有如下形式:

對于下式所示的時域閉環混合B-J模型:

基于預測誤差最小化,第k 個采樣時刻的誤差函數可表示為:

公式的預濾波形式為:

公式(9)的預濾波線性回歸表達式可表示為:

其向量參數表達式為:

其中:

圖形1所示閉環系統的無干擾過程時域模型可由下式計算出:

其預濾波形式可由下式得出:

公式(15)的預濾波輔助變量模型表達式為

最終的輔助變量優化公式如下所示:


反饋噪聲消除的閉環辨識算法
CLRIVC實現了閉環混合B-J模型閉環辨識,但過程模型的初始值偏離真值較遠時,有時會出現收斂性差的問題。在分析圖1結構的基礎上,本文提出了新的消除反饋噪聲的混合B-J模型閉環辨識改進算法(DNIV)。新算法將原來算法中的由過程輸入輸出的預濾波數據作為過程模型向量更新為不含反饋噪聲成分的過程輸入輸出預濾波數據作為過程模型向量。
對于 圖1所示的時域閉環模型方程可推導出:

令:

由公式(15)、公式(20)和公式(21)可推導出:

由公式(21)可知,vn(tk)為反饋噪聲產生的控制器輸出,為干擾產生的過程模型輸出成份。
將公式(22)中u(tk)代入過程模型:

推導出不含反饋噪聲成份的過程模型:

新算法以公式(15)求解不含循環噪聲成份的x(tk)和v(tk),以公式(24)計算出不含反饋噪聲成份的過程輸出yc( tk),以yc(tk)和v(tk)的預濾波數據建立過程向量:

輔助向量:

由x(tk)和v(tk)的預濾波數據建立,以公式(18)實現混合Box-Jenkins模型的過程參數辨識。算法的過程描述如下:
2)設定初始循環j=1和最大循環次數Itrmax

4)使用預濾波器f (i )=pi/A(p)計算連續預濾波變量值
c
5)計算有色噪聲ξ(tk)=y(tk)-x(tk),使用IVARMA算法辨識噪聲模型Gn,令fd=1/Gn,根據和計算預濾波變量值和
4 改進算法的仿真測試
為了驗證算法的有效性,首先對算法進行仿真驗證,給定過程傳遞函數模型如公式(26)所示:

選擇如下的PI控制器:

干擾模型為一階模型,公式如下:

仿真使用的設定值幅值為±1, 分段連續的激勵信號, 系統響應數據應用零階保持器,以采樣間隔為的速率獲取,數據量取N=3000。應用Monte Carlo Simulation(MCS) 分析方法隨機產生100組高斯白噪聲,通過調整高斯白噪聲的方差,產生設定值與有色噪聲的信噪比為10dB的有色噪聲信號。
為了驗證算法的尋優效果,應用同樣的閉環輸入輸出,分別使用中CONSTID工具箱中CLRIVC算法,MATLAB的系統辨識工具箱中的PEM連續B-J模型計算方法和DNIV算法進行仿真。三種算法的100組MSC仿真結果見表1。表中列了三種方法的100組數據計算結果均值,結果標準差和平均絕對誤差和MAE 。MAE 定義為:
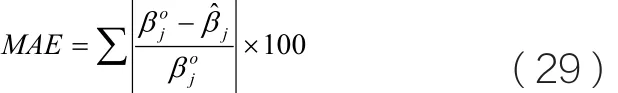
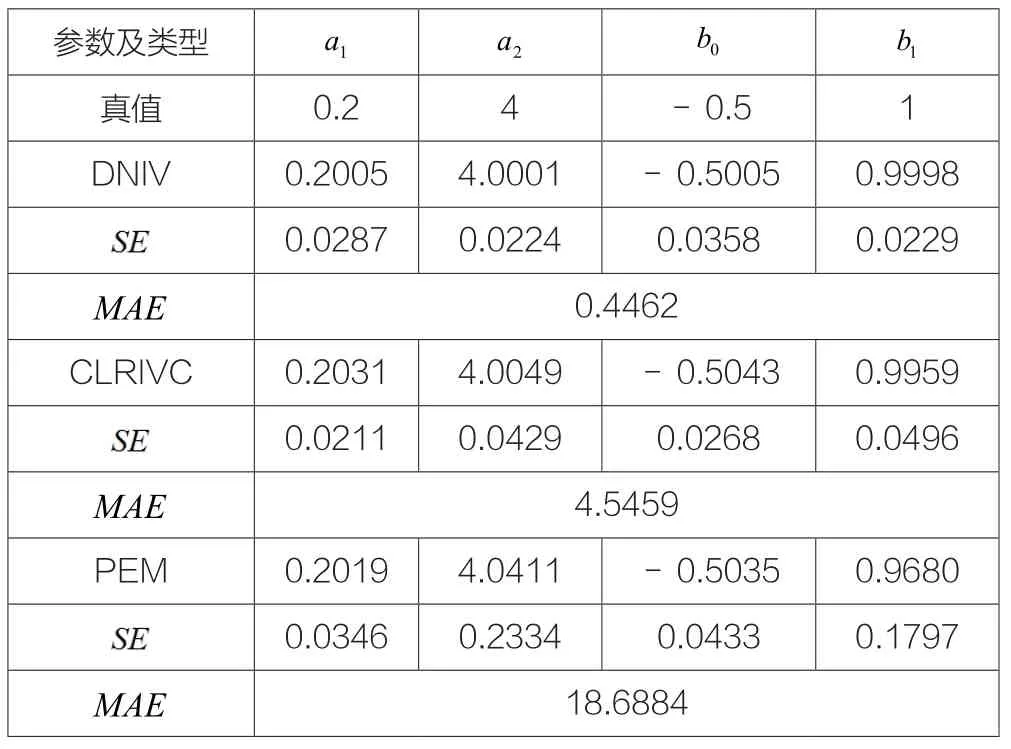
表1 三種算法的MSC仿真結果表
從表中的結果可以看出盡管CLRIVC算法中的部分參數的標準差略優于DNIV算法,但DNIV的參數均值和MAE均優于CLRIVC的計算結果,而PEM算法雖然能得到較好的結果,相對于DNIV和CLRIVC來說,效果較差。
結論
在裝置正常生產條件,針對閉環控制回路,過程的輸入輸出數據存在一定的相關性,傳統的開環辨識算法結果不理想問題提出了連續時間閉環混合Box-Jenkins模型辨識方法,為提高噪聲模型的辨識精度,提出了帶有懲罰因子的極大似然參數估計算法。DNIV算法首先基于最小二乘狀態變量濾波獲取初步的過程模型參數,然后剔除回路數據中的循環干擾成份,以輔助變量算法進行混合Box-Jenkins模型辨識,從而獲取更精確的過程模型參數。仿真實驗證明了算法的有效性。
10.3969/j.issn.1001- 8972.2016.19.036