模塊化多級水火箭設計與模擬
侯沐朗
(北京市第四中學,北京 100120)
?
【基礎理論與應用研究】
模塊化多級水火箭設計與模擬
侯沐朗
(北京市第四中學,北京100120)
研究了利用現有容器實現多級水火箭的設計方案,分析了捆綁式二級水火箭的設計思路。第一級由三個耐壓儲水罐組成,第二級有一個耐壓儲水罐;重點分析了火箭噴水推進階段的數學物理模型,空氣阻力對系統的影響,最優儲水量,多罐壓力平衡等關鍵問題。利用計算機對火箭整個飛行過程進行了理論計算和描述,為在簡陋條件下自行研制各種結構的水火箭提供了思路。
多級水火箭;多罐壓力平衡;火箭分離;最優水量
水火箭結構簡單,原材料普通且廉價,并且在制作過程中能夠應用現代火箭的一些基本理論知識,宜于廣大中小學生實踐制作。簡單的水火箭結構以單級為主,上升高度受到了水量、容積等多方面限制。
捆綁式多級水火箭的第一級由三個儲水罐組成,第二級為單獨的儲水罐。本文分析了水火箭飛行過程數學模型,以及一定容積的最優儲水量,提出了一種簡單易行的多罐壓力平衡解決方案。文章用具體的實驗數據與理論計算值進行比較,優化了整體設計,制作了實體水火箭并進行實驗。
1 多級水火箭結構
多級水火箭的第一級選取三個容量為2.13L的廢舊飲料瓶。其材質為PC(聚碳酸酯),瓶壁厚度為0.22mm,實測耐壓強度約為9個大氣壓。三個一級儲水容器通過橡膠繃帶捆綁固定。為了防止火箭飛行過程中由于三個儲水容器的推力不一致導致飛行姿態紊亂,要保證水火箭第一級三個儲水容器內壓一致。設計了一種簡單的連通器,如圖1所示。連通器的三個端口分別置于三個容器的頂部,與各個瓶內空氣容腔相連通,保證其壓力平衡。并且,由連通器的總端口負責火箭初始階段的加壓操作。
第二級水火箭的結構與材料與第一級水火箭完全一致,這樣做的目的是減少工作量,使水火箭模塊化。將第二級火箭的結構放置在第一級上部,由分離裝置固定,分離裝置由電磁繼電器等元器件組成。多級水火箭的整體結構如圖2所示。在第二級火箭的結構的瓶臂上,固定著水火箭控制系統,系統電路示意圖見圖3。電路的核心由AT89C52單片機構成,板上集成了多種傳感器負責采集實際飛行過程中的物理參數,如:氣壓傳感器(型號:BMP085)、加速度傳感器(型號:ADXL345)和磁場傳感器(型號:HMC5883L)。控制電路還負責水火箭點火以及水火箭分離的操作,是整個水火箭的核心部件。
2 基本理論與實驗
2.1推進階段
水火箭的唯一動力是依靠瓶內高壓推射出水,根據牛頓第三定律,推射出的水反作用于水火箭,從而推動水火箭上升。由于水火箭儲水瓶內壓很高(7~9大氣壓),而且由于結構原因,存儲的水量不多,每個儲水瓶一般不超過2L,因此水會在瞬間噴射完畢。
根據tsiolkovsky火箭方程[1],對于單個火箭儲水容器有:
(1)
其中,FT為噴水過程中的推力,ve為水噴射的瞬時速度,m為噴射出水的質量,t為時間。物體的質量與其密度與體積有關,因此:
(2)
ρw為液體質量,V為液體體積,因此可以得到:
(3)
AN為噴嘴的橫截面積。根據式(3),將水的質量變化率轉換成了橫截面與噴速的乘積形式。
水火箭噴嘴的水流速可以用伯努利方程描述[2-3]。伯努利方程假定水不能壓縮并且無粘性。根據伯努利方程有:
(4)
其中,P為儲水容器的瞬時內壓(Pa),Patm為標準大氣壓(Pa)[4],vi為容器內水相對與火箭的速度(默認為0)(m/s),g為重力加速度(N/kg),y為水在容器內的高度(m)。通過伯努利方程可以求出水噴速與容器內壓的瞬時關系:
(5)
水火箭在推進階段水在不斷的流失,因此空氣的體積也會隨著水的減少而不斷的增加。空氣的體積增大必然導致瓶內氣壓變化,這個變化關系可以用理想氣體恒溫膨脹方程[5]來表示。應用此公式的前提是氣體的溫度不變。氣體體積與壓強的關系可以用如下公式表示:
(6)
其中,P0為初始瓶內氣壓(Pa),V0為初始氣體體積(m3),ΔV為體積的變化量,r為絕熱系數[6](常數),空氣的絕熱系數為1.4。
整體上,火箭所受的矢量力為:
(7)
(8)
mr是火箭的質量(kg),mw是火箭現有的水質量(kg),F為火箭受力之和(N),Fg為火箭所受重力(N),重力貫穿整個飛行過程。
由于整個推進階段各個關鍵量如水量、瓶內壓、水的噴射速度都在不斷變化,因此根據公式得到的結果誤差較大。在計算推進階段的各項指標時,先需要確定火箭的基本參數,如:液體密度、液體重量、瓶內壓、瓶質量、噴嘴直徑等參數。然后根據公式上述公式,求出初始噴速、初始推力等初始量,最后根據上述初始量一步一步模擬整個推進過程。
2.2慣性階段
推進階段完成后,由于此時只剩下部分氣體的推進動力,氣體動力較小。為了計算方便,在此可將其忽略。此時火箭所受的外力只有重力與空氣阻力[7-8],重力為:
(9)
空氣阻力為:
(10)
空氣阻力的大小與物體速度的平方成正比。Cp為空氣阻力系數(常數),與物體外形相關,文中取0.35[9];ρa為空氣密度(kg/m3);Af為迎風面積(m2)。
根據簡單的力學公式就能求得飛行過程中的加速度a與飛行速度vn:
(11)
(12)
根據上述飛行過程中的加速度a與飛行速度vn兩個值與時間就可以確定飛行高度H。
由于此時火箭的上升完全是憑借推進階段結束后的速度上升,其上升的最高點即上升速度為零的時刻。第一級水火箭體之高度與時間的曲線呈開口向下的拋物線狀。通常情況下,分離在水火箭第一級產生的初始速度耗盡時刻,也就是第一級水火箭達到的最高處。根據實際操作情況,分離發生在第一級水火箭推進階段完畢的一秒鐘以后。之所以選擇這個時間節點,一方面是此時空氣阻力下降,水火箭的上升速度也下降;另一方面是由于第一級水火箭儲水容器中剩余的壓縮空氣仍有壓力,能起到助推作用。
第一級與第二級水火箭分離后,二級水火箭的飛行過程也分為推進階段與慣性階段,只是第二級水火箭的初速度與飛行高度均不為零,分析過程與對第一級水火箭的分析完全一致。
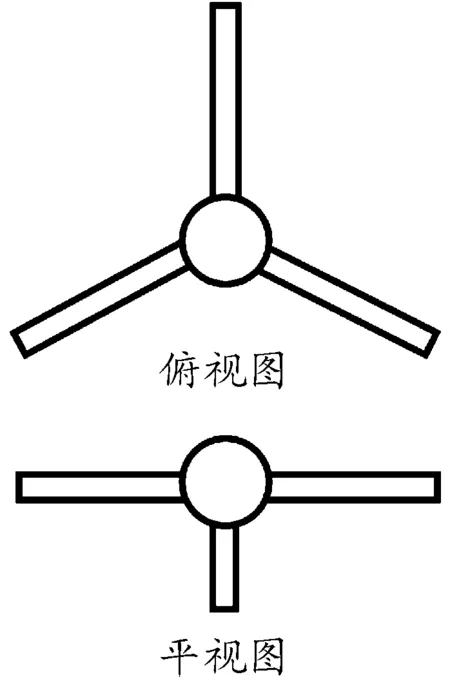
圖1 壓力均衡連通器
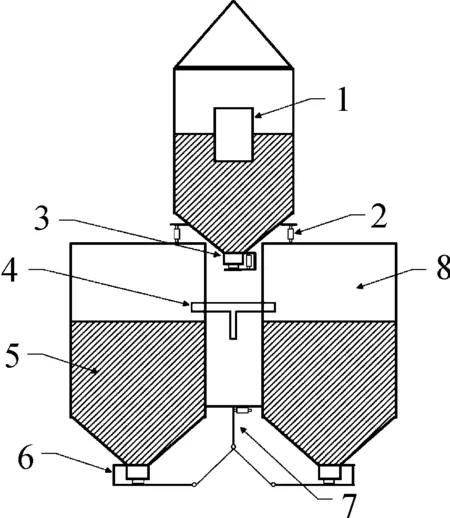
1.火箭控制系統; 2.一、二級火箭分離器; 3.二級火箭發射裝置; 4.一級火箭壓力平衡及加壓裝置; 5.水; 6.一級火箭噴口; 7.一級火箭同步發射裝置; 8.空氣容腔
圖2多級水火箭的整體結構示意圖
2.3最優填水量
水火箭第二級的質量與第一級的水量是影響水火箭飛行高度的關鍵參數。水火箭第二級質量越小越好,這樣第一級的推力能夠使水火箭產生較大的加速度,但是質量過小,制造成本大。另一方面,水火箭儲水容器水量的確定更為重要[10]。若裝載的水過少,噴射時間太短,水火箭的推進階段時間過短,無法達到一定的速度,因此后續階段飛行高度會下降;若裝載的水過多,總體質量增大,加速度會變小,也會影響到飛行高度。因此,需要找到一個合理的水量與容積的比值。
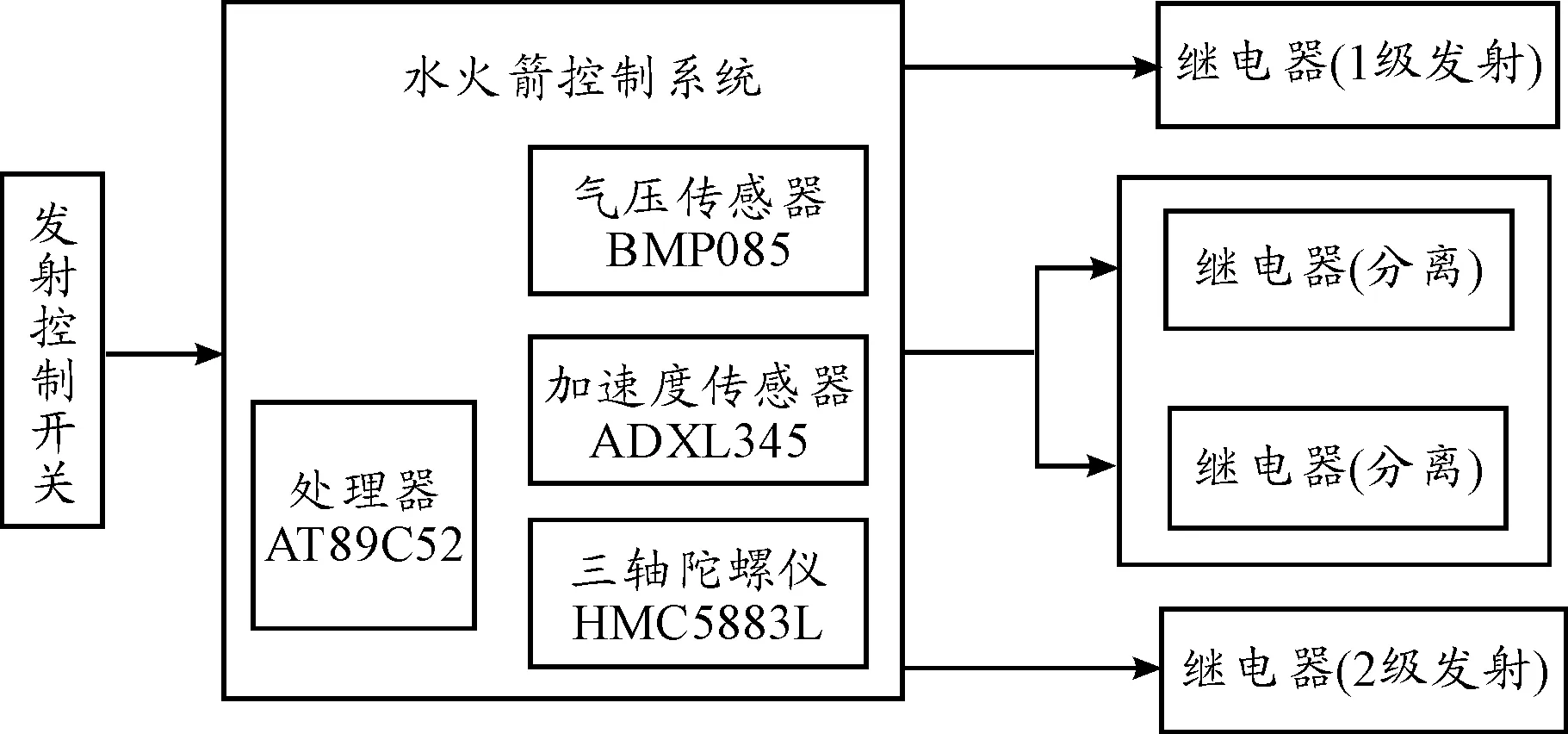
圖3 控制電路示意框圖
水火箭的整個飛行過程在前面已作分析,在優化求解參數時,先將需要的參數值設置為一定范圍。設msi為第二級水火箭的質量,其取值范圍為[0.05 kg,1.45 kg],設mwi為第一級水火箭填充的水質量,其取值范圍為[0.05,1.45]kg;由于有兩個變量,采用網格搜索法[11],求出水火箭的最終高度,取最高點。對應于水火箭最高點的第二級水火箭的質量和第一級水火箭填充的水質量,即為最優參數。其結果如圖4所示。
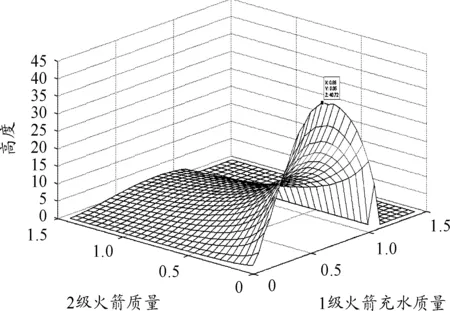
圖4 二級水火箭質量與一級火箭填充水量對飛行高度的影響
圖4中Z軸是飛行高度,是所需要最大化的目標量。可以很明顯的觀察到,二級水火箭的質量越小越好,而填充的水量需要保持在一個適當的位置,過多過少都不能達到最優。從圖中還可以發現,與二級火箭質量多少無關,第一級水火箭的最優填充水量與第一級水火箭能容納的最大水量之比為0.433。
2.4實驗及其分析
具體水火箭實驗的各項參數見表1與表2。
各項參數確定后,可根據2.1與2.2節中的各項公式通過計算機模擬火箭的飛行過程。設時間增量Δt=0.001 s。
一級水火箭推進階段之火箭速度曲線如圖5所示。從圖5可以看出整個過程的時間很短,在0.43 s時間內水火箭從零加速到22.34 m/s的速度。
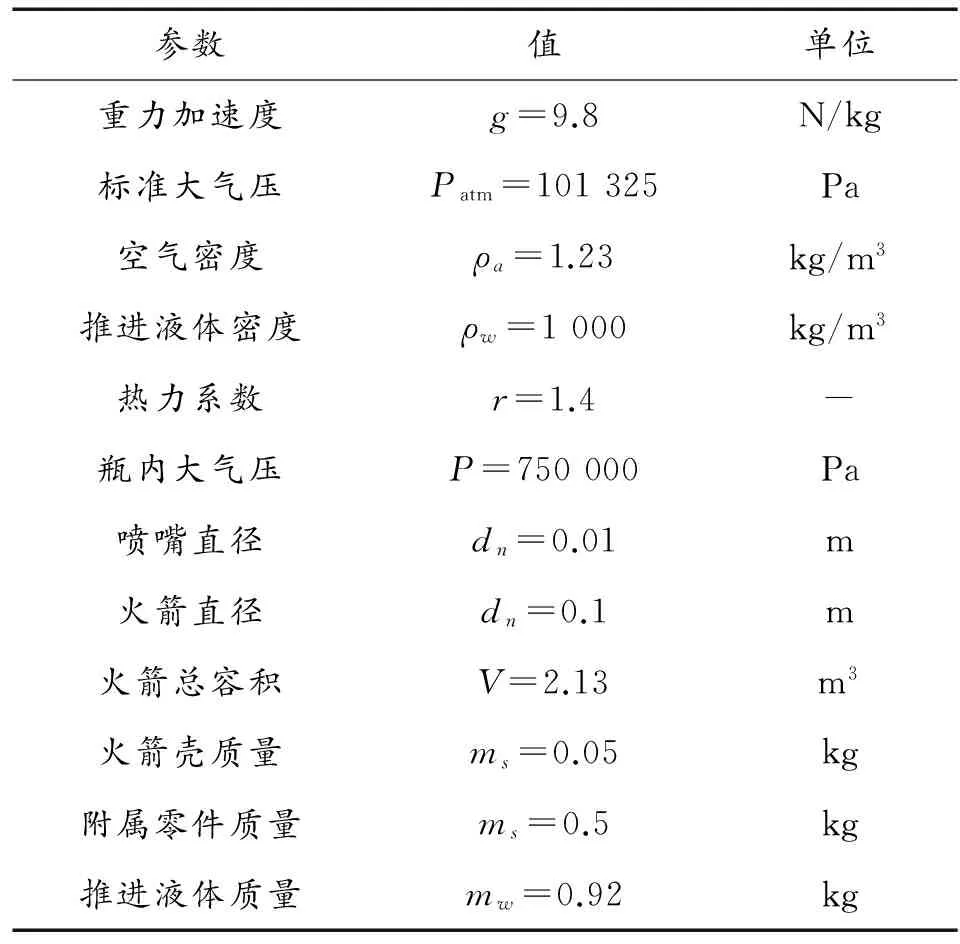
表1 第一級水火箭基本參數
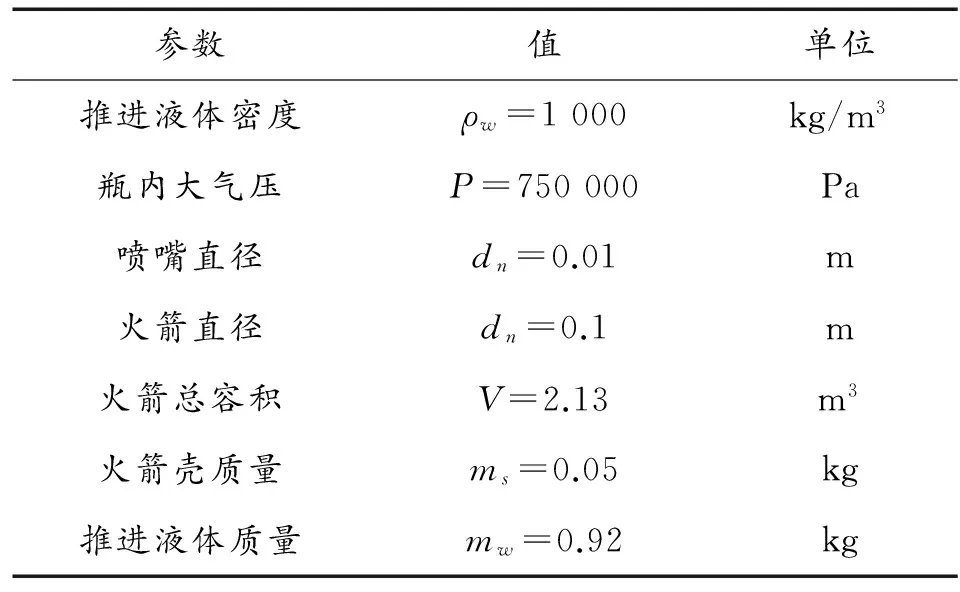
表2 第二級水火箭基本參數

圖5 一級水火箭推進階段速度曲線
第一級水火箭推進階段其余參數,如第一級水火箭噴水速度、總體受力見圖6和圖7。通過模擬可知,第一級火箭推進階段最大受力為262.80 N,上升高度為4.8 m。
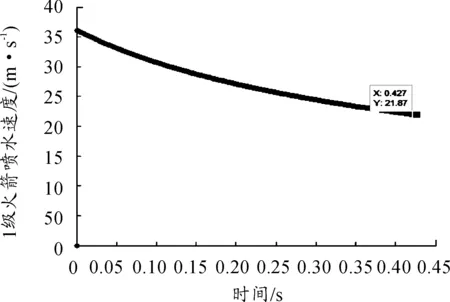
圖6 一級水火箭推進階段噴水速度曲線
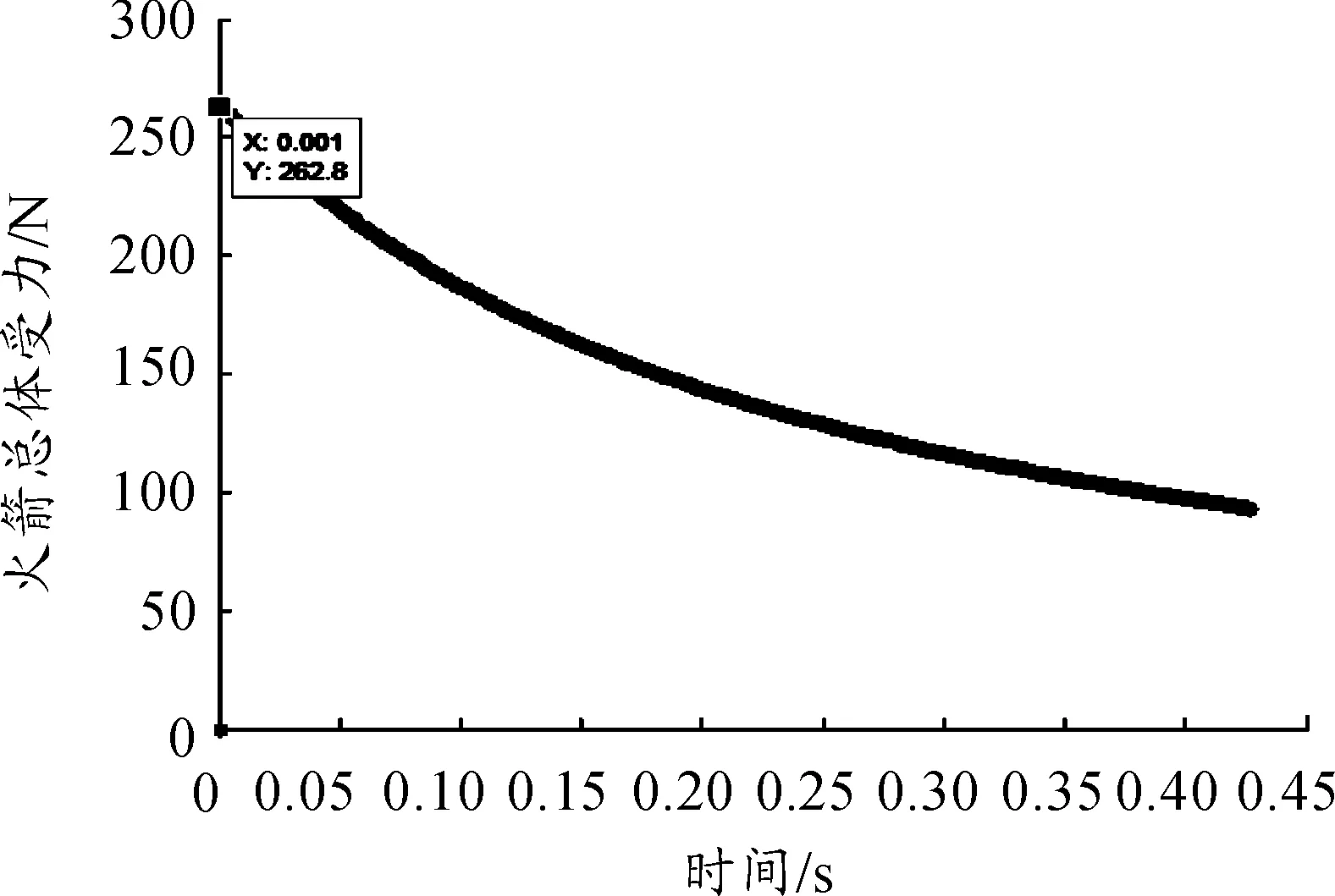
圖7 一級水火箭推進受力曲線
第一級水火箭推升階段完畢后,水火箭上升一秒鐘時間,一二級水火箭開始分離,此時受重力與空氣阻力影響。分離時,第二級的初始速度為:11.62 m/s,分離高度為:21.68 m。分離前水火箭速度與高度數據曲線如圖8所示。
第二級水火箭分離后,分離運動量成了第二級火箭的初始量,其推進階段和慣性運動階段運動參數的確定與第一級火箭的確定方法一致。水火箭總體運動過程如圖9所示。從圖9可以發現,第一級水火箭推進階段,分離階段,第二級水火箭推進階段,第二級水火箭慣性飛行階段在圖中都有明顯的區分節點。總體上水火箭在空中最大飛行速度為74.79 m/s,總體上升高度理論上能夠達到136.5 m。
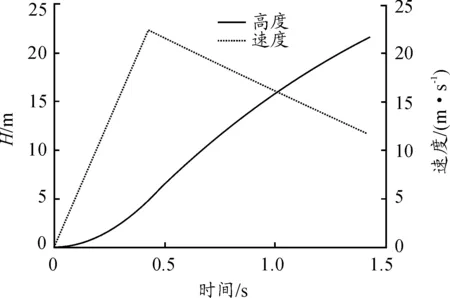
圖8 水火箭分離前速度與高度曲線
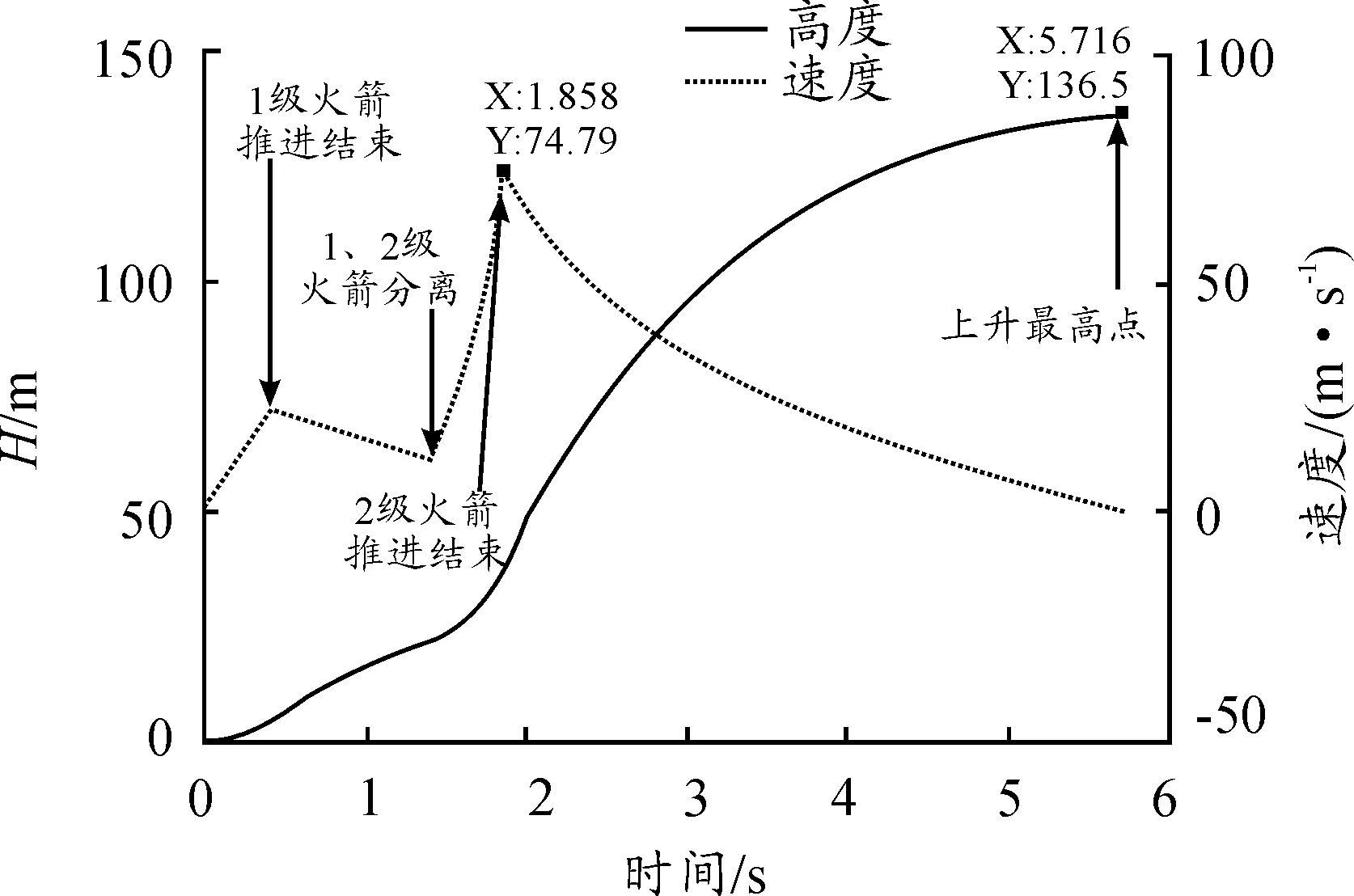
圖9 水火箭全過程速度與飛行高度曲線
將水火箭第一級與第二級的水相加,然后平均分配到一級火箭的三個桶中。按照表1與表2的數據,第一級水火箭每個模塊中水量為1.227 kg,第二級水火箭水量為零,動力全部由第一級水火箭提供,第一級和第二級水火箭整個飛行過程不分離,其他參數不變。將數據代入模型擬,結果如圖10。可以看到,整個火箭飛行時間為3.335 s,飛行高度為48.07 m。采用二級結構的水火箭飛行高度是一級水火箭飛行高度的2.84倍。
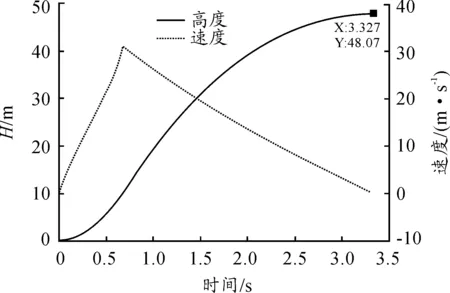
圖10 同等質量的推進液體情況下一級火箭飛行情況
3 結論
水火箭的制作簡單易行,適合人們鍛煉動手能力與理論水平,并且能夠引導初高中學生對航天科學的興趣。文章為了分析方便,忽略了液體推進完畢后瓶內剩余氣壓的影響,在計算實際的水火箭飛行過程時會產生一定的偏差。
[1]FINNEY G A.Analysis of a water-propelled rocket:A problem in honors physics[J].American Journal of Physics,2000,68(3):223-227.
[2]LE MéHAUTé,BERNARD.The Bernoulli Equation[M].An Introduction to Hydrodynamics and Water Waves.Springer Berlin Heidelberg,1976:101-115.
[3]陳燕黎.伯努利方程的原理及運用淺析[J].漯河職業技術學院學報,2012,11(2):86-88.
[4]王玉忠.確定標準大氣壓的歷史沿革[J].物理教學探討,2001,19(10).
[5]楊紀文.理想氣體狀態方程——從經典到量子[J].物理,2003(5):6-8.
[6]田春山.利用新型超聲波傳感器測定空氣絕熱系數實驗[J].青海大學學報:自然科學版,2003,21(4):52-53.
[7]PUGH,LEWIS GRIFFITH CRESSWELL EVANS.Oxygen intake in track and treadmill running with observations on the effect of air resistance[J].The Journal of physiology,1970(3):823-835.
[8]陳南翼,張健.高速列車空氣阻力試驗研究[J].鐵道學報,1998(5):40-46.
[9]BARRIO-PEROTTI R,BLANCO-MARIGORTA A D K,FERNANDEZ-ORO J.Experimental evaluation of the drag coefficient of water rockets by a simple free-fall test[J].European Journal of Physics,2009,30(5):1039-1048.
[10]呂宗友,陳曉莉,王柏廬.水火箭的制作與發射[J].物理教學探討,2002,20(9):44-45.
[11]王健峰,張磊,陳國興,等.基于改進的網格搜索法的SVM參數優化[J].應用科技,2012(3):28-31.
(責任編輯楊繼森)
DesignandSimulationofModularMultistageWaterrocket
HOUMu-lang
(BeijingNo.4MiddleSchool,Beijing100120,China)
Basedontheexistingcontainerdesignscheme,howtorealizemulti-stagewaterrocketwasanalyzed,andthebundledsecondarywaterrocketdesignideaswasresearched.Thefirststagewasconsistofthreepressurewatertankcomposition,andthesecondstageisapressurewatertank;thispaperfocusedontheanalysisoftherocketjetpropulsionphaseofthemathematicalandphysicalmodel,theinfluenceoftheairresistanceofthesystem,theoptimalwaterstorage,themultitankpressurebalanceandotherkeyissues.Atthesametime,usingthecomputerwecalculatedanddescribedthewholeflightprocessoftherocket,anditprovidespracticalideasformiddleschoolstudentstodevelopvariousstructuresofwaterrockets.
multistagewaterrocket;multitankpressurebalance;rocketseparation;optimalwaterquantity
2016-05-05;
2016-05-20
侯沐朗(1999—),男,主要從事航空航天技術研究。
10.11809/scbgxb2016.09.042
format:HOUMu-lang.DesignandSimulationofModularMultistageWaterrocket[J].JournalofOrdnanceEquipmentEngineering,2016(9):188-192.
V19
A
2096-2304(2016)09-0188-05
本文引用格式:侯沐朗.模塊化多級水火箭設計與模擬[J].兵器裝備工程學報,2016(9):188-192.

