重組練習材料 提升思維品質

陳瑾

教學人教版五年級上冊《三角形的面積》之后，我發現教材中的練習題大多是利用面積計算公式，直接求面積，或者求高或底，而這些都是學生早就熟練掌握的內容。那么，在基礎性學力之外，發展性學力、創造性學力如何兼顧？

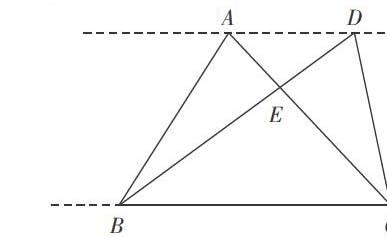
教材安排了一道練習題，在兩條平行線中尋找面積相等的三角形（見下圖），并畫出與原三角形面積相等的三角形（見下圖）。這道題背后隱藏的“等積變形”思想是圖形與幾何領域的重要思想方法之一，也是初中學習幾何證明時常用的方法。因此，我充分利用這道題，在材料重組方面下功夫，引導學生體會等積變形的思想方法，培養空間觀念，達到提升思維品質的目的。

一、經歷分層探究的過程，拓寬思維的廣度

關注學生的學習基礎與學習能力，創設簡潔的情境，一題多變，促使學生在靈活運用三角形面積計算公式的基礎上分層探究，在直觀感受與動手操作中進一步理解“等底等高，面積相等”的含義，真正弄清知識的來龍去脈。

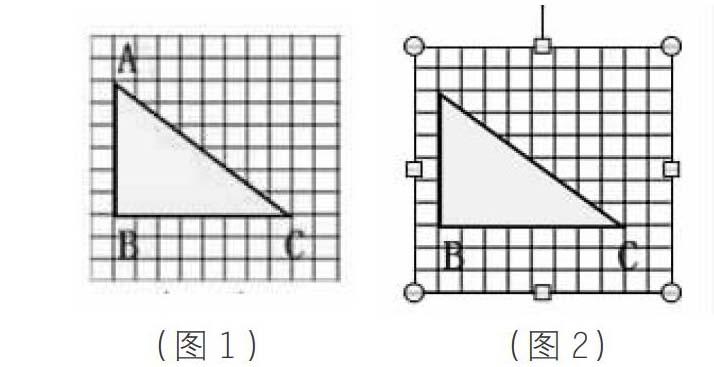
【案例1】在方格紙中分別以下面直角三角形的BC、AB、AC三條邊為底，畫出與它面積相等的三角形。（見圖1）

環節一：以直角三角形的BC邊為底，畫出與它面積相等的三角形。（見圖2）。

反饋：先選擇學生的作品展示，再引導學生理解：這些三角形的形狀完全不同，但是等底等高，所以面積肯定相等。

師：像這樣的三角形還能畫嗎？你能快速找到它們嗎？

生：我畫一條與BC平行的平行線，可以很快找到無數個這樣的三角形。

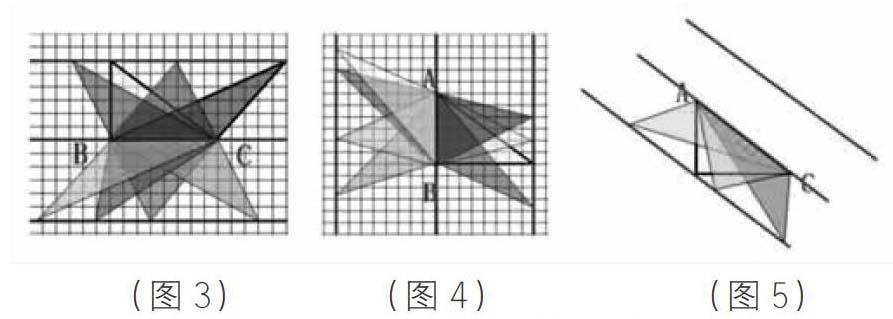
再引導學生發現平行線可以朝上畫，也可以朝下畫，所以這樣的三角形有無數個。隨后課件演示。（見圖3）

師：因為這些三角形等底等高，所以面積肯定相等。即使形狀千變萬化，但是面積始終不變，這就是我們在數學學習中通常說到的“等積變形”。

環節二：請在頭腦中想象，以直角邊AB為底，畫出與原三角形面積相等的三角形。學生先獨立思考，教師再用課件演示以AB為底的畫法。（見圖4）

環節三：出示一幅沒有方格的圖，學生以斜邊AC為底，畫出與原三角形面積相等的三角形。

先反饋學生作品，再演示課件上的畫法，接著教師再用電子白板演示在平行線上拉動三角形頂點，形狀改變但面積不變的過程。（見圖5）

小結：不管平行線是橫向還是縱向，或者是斜向的，只要三角形的一條邊在平行線上，對應頂點在另一條平行線的任意位置，所形成的無數個三角形都和原三角形面積相等，因為它們既等底又等高。

同一素材一變再變，三個環節環環相扣，在充分感受“等底等高，面積相等”的基礎上，將思維提升到“等積變形”的高度，把剛才的探究過程整理如下表：

二、體驗多樣的解題策略，提升思維的靈活度

“為班級學習共同體提供有一定難度的問題”是集體學習材料理想的標準，無論是蘇聯的贊科夫還是日本的佐藤學，都是同樣的觀點。先讓學生充分地自主嘗試，然后互相交流，互通有無，體驗多樣的解題策略，真正學有所得，從而提升思維的靈活度。

【案例2】求出下面陰影部分的面積。

方法1：用大面積減小面積的方法做。先求大梯形的面積，再減去空白部分三角形的面積，得到的就是陰影部分的面積即32平方厘米。

方法2：因為兩個陰影部分的三角形等高，所以可以把左邊陰影部分三角形變形，移動頂點和右邊的三角形拼在一起，組成一個規則的大三角形，底是16厘米，高是4厘米，所以面積是32平方厘米。

然后教師引導一名學生用電子白板演示拉動頂點等積變形的過程。學生認真觀察，紛紛笑瞇瞇地點頭，表示和自己想的一樣。（見圖7）

師：還可以怎么變？

方法3：把右邊的三角形往左拉，也可以拼成一個底是16厘米、高是4厘米的大三角形，兩種方法本質上是相同的。（見圖8）

方法4：既然可以往左拉，往右拉，那么肯定可以從兩邊同時往中間拉。平行線上有無數個點，所以就有無數種拉的方法。（見圖9）

師：同學們的腦子真靈活呀，真是一點就通！（伸出大拇指表示贊賞）

當學生在經歷“山重水復疑無路”的無奈之后，在對比和碰撞中打破思維平衡，在解決具體問題的過程中體驗策略多樣化，并感悟“等積變形”方法的便捷性，最終收獲“柳暗花明又一村”的喜悅。

【案例3】求出不規則四邊形的面積。（見下圖10）

方法1：添加幾條線，補出一個大長方形，就能很明顯看出兩個三角形的面積之和就是這個長方形面積的一半，所以直接用長方形面積除以2。（見圖11）

方法2：假設上下兩個三角形的高分別是h1和h2，求總面積用6h1÷2+6h2÷2，可用乘法分配律變形為（6h1+6h2）÷2，再到6（h1+h2）÷2，最后得到6×9÷2，結果也是27平方厘米。（見圖12）

方法3：用等積變形的方法，把上面三角形的頂點平行拉動到右邊，直到把兩個三角形變成一個規則的大三角形為止。求總面積仍然用6×9÷2，結果還是27平方厘米。（見圖13）

同學每介紹一種做法，老師都真誠贊揚，其他同學也報以熱烈的掌聲。

小結：三個同學，三種思路，都可以用算式6×9÷2來解決，相比較而言，我們通過移動頂點，運用等積變形的方法來做（見圖13），顯然更加簡單。

這兩道習題的設計是經過深思熟慮的，既可以用常規方法來做，又能利用轉化思想，用“等積變形”的方法來解決，策略選擇的多樣化能滿足不同層次的學生的需求。

三、提供富有張力的材料，挖掘思維的深度

數學教學要適當追求學生對知識理解的深刻性，教師要善于捕捉與尋找復雜的、有張力的、有豐富內涵的關系，使教學材料呈現豐富的結構，從而促使學生的思維更有深度。

【案例4】下圖是由邊長分別為5厘米和4厘米的兩個正方形組成，求陰影部分的面積。

方法1：用兩個大正方形的總面積減去空白部分，也就是三個小三角形的面積，就得到陰影部分的面積。

師：同學們用常規方法——大面積減去小面積來做，很好！但是，解決這道題還有更加巧妙的方法，我們是否可以從等積變形的角度思考呢？

學生獨立思考，然后交流。

方法2：我把陰影部分看成兩個小三角形，分別等積變形，可以變成一個底和高都是4厘米的大三角形BEF，面積是8平方厘米。（見圖14）

師：非常棒，真是奇思妙想！（大家紛紛為這位同學獻上熱烈的掌聲。）

師：還有別的想法嗎？如果沒有，老師給個提示（課件出示平行線），同學們再嘗試解決。

方法3：以陰影部分三角形的一條邊為底，將它對應的頂點在這組平行線之間移動，移到它變成一個直角三角形為止。這個直角三角CEG形恰好是小正方形面積的一半，所以面積就是4×4÷2=8平方厘米。（見圖15）

有的同學還在思考，有的同學一下就看明白了，發出一聲驚呼。老師再借助電子白板，動態呈現在一組平行線之間移動三角形頂點等積變形的過程，這時更多學生露出會心的笑容。接下來，同桌之間對這道題如何采用等積變形的方法再次討論，交流。

師：你能像剛才這樣，在這幅圖再創造出兩個面積相等的三角形嗎？試一試吧。（見圖16）

在數學學習中，教的立足點是促進學生的學。從學生實際出發，通過教材重組，提供合適難度的練習，滲透數學思想方法，是培養學生思維不可或缺的要素，也是提高學生數學素養不可忽視的途徑。

（作者單位： 浙江省杭州市文海實驗學校）

責任編輯 曾維平

E-mail：25365420@qq.com