磁彈效應索力傳感器的差動式溫度補償及試驗研究*

馮志敏，邵　磊，陳躍華

（寧波大學海運學院，浙江寧波315211）

磁彈效應索力傳感器的差動式溫度補償及試驗研究*

馮志敏*，邵磊，陳躍華

（寧波大學海運學院，浙江寧波315211）

在研究旁路結構的磁電復合材料索力傳感器檢測方法基礎上，運用鐵磁性分子場理論和布洛赫自旋波方法，建立磁化強度與溫度的函數關系，研究溫度對檢測精度的影響機理。提出一種并行裝配的溫度補償傳感器磁路結構，運用差分運算技術，設計具有分時共享信號調理功能的差動式信號處理電路，實現全溫度范圍的差動式自動補償。試驗表明，在0～20 kN變載下，-30℃～+80℃溫度范圍內，對誘導電壓信號的波動影響小于1%，測量重復誤差0.04%～0.30%，有效解決了溫度補償難題，能夠滿足索力檢測工程要求。

索力傳感器；溫度補償；差分技術；磁電復合材料；磁化強度

EEACC:3120；7230doi:10.3969/j.issn.1004-1699.2016.07.006

近年來，由于鋼纜索具有柔性大、強度高、頻率低等特點，已廣泛應用于各種大型建筑作為承力構件，精確檢測鋼纜索受力狀態是保證建筑結構安全可靠運營的關鍵。磁彈效應法是一種動態響應快、測量精度高、可實現全天候動態實時測量的新穎索力檢測方法［1-3］。由于鐵磁材料的磁化性能受溫度影響，其影響因子與材料型號、外加磁場強度及溫度場的梯度方向（升溫或降溫）直接有關，因此，磁彈效應法受溫度影響較大，對傳感器制備技術提出較高要求，需要采取有效的溫度補償方法，使傳感器獲得精確的參數檢測。美國著名的磁彈性傳感器研究者Wang M L，在溫度曲線法基礎上利用插值法消除溫度影響，進行大量試驗研究［4-5］，日本的相關學者對溫度曲線法進行了深入研究［6］，這些算法適合特定范圍的溫度補償。本文通過研究旁路式結構的磁彈效應索力傳感器檢測方法及其溫度對檢測精度的影響機理，提出了一種并行裝配的溫度補償傳感器結構，結合差分運算技術，實現全溫度范圍的差動式自動補償，試驗表明了系統能夠滿足索力檢測的實際要求。

1　原理與模型

1.1檢測原理

磁彈效應索力傳感器的旁路式結構如圖1所示。將軛鐵和磁極過盈裝配后，把預先制備的磁電復合材料嵌入磁極的軸向凹槽中，并在磁極外側纏繞覆蓋激勵線圈，用磁極夾具將鋼纜索固定。

圖1　旁路式傳感器結構

磁電復合材料由磁致伸縮層/壓電材料/磁致伸縮層［7-9］膠合制成，如圖2所示。磁致伸縮層為Terfenol-D合金，M表示其磁化方向，壓電材料為PMN-PT壓電晶體，P表示其極化方向。激勵線圈通入電流I，鋼纜索軸向被磁化。鋼纜索的受力狀態發生變化時，纜索的軸向磁通量相應改變，磁致伸縮層因感應軸向磁通量的變化，其長度方向產生一定變形。由于壓電層與磁致伸縮層被高強度材料粘結于一體，壓電層隨著磁致伸縮層變形產生協調變形，從而由機械-電耦合發生電極化產生誘導電壓。只要檢測壓電晶體的輸出誘導電壓就直接獲得鋼纜索所受外力大小。

圖2　磁電復合材料

1.2數學模型

根據磁彈效應數學模型［10-11］

式中，σ是鋼纜索應力，B是感應磁場強度，H是磁場強度，L是磁化鋼纜索長度。

Terfenol-D/PMN-PT/Terfenol-D層狀磁電復合材料的磁轉換系數為［12］

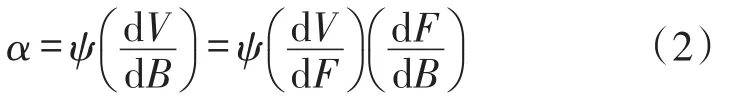
由式（1）和式（2）可得磁電復合材料輸出的電壓

式中，?在一定磁場中，是鐵磁性復合材料的材料常數；表明電壓V與鋼纜索應力σ呈線性關系。

2　溫度誤差補償

置于磁場中的鋼纜索其磁化強度與外加磁場強度、受力狀態以及環境溫度直接相關。由磁化強度的變化來測量索力，需消除其他兩個因素產生的影響。實際檢測中，通過施加恒定磁場來消除外加磁場強度的影響，但環境溫度的變化難以預測和控制，溫度產生的影響無法直接予以消除。

2.1溫度影響機理

當鐵磁體置于外加磁場中被磁化時，其磁化強度M與磁場強度H的關系為

式中，?為磁化率。如果被測對象為鋼纜索，屬鐵磁性材料，其磁化強度M和溫度T的關系呈復雜的非線性關系。

由鐵磁性分子場理論［13］可知，鐵磁材料的磁化強度與溫度的關系為

式中，B（y）為布里淵函數；λ為朗德因子；μ為波爾磁子；S為總自旋角量子數；N′為單位體積內原子的個數。

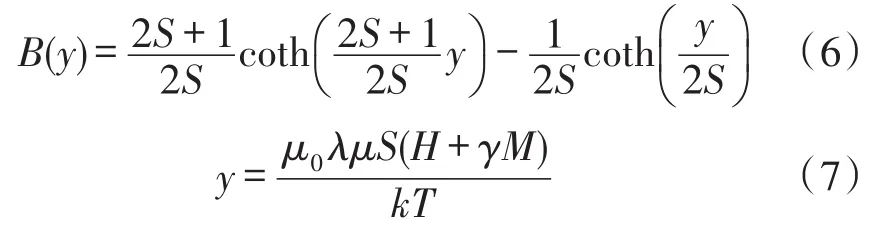
式中，μ0為真空磁導率；γ為外斯分子場系數；k為波爾茲曼常數；T為溫度。設M0=N′λSμ，是絕對零度下磁化強度的最大值，即絕對飽和磁化強度，則有

由式（7）和式（8）得方程組

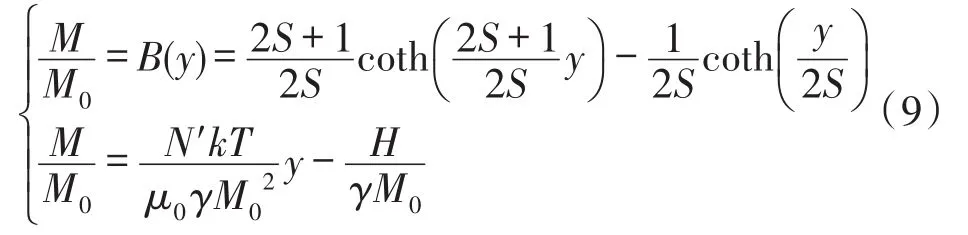
求解式（9），可得一定磁場和溫度條件下的磁化強度。

根據分子場理論得到的鐵磁體磁化強度與溫度的關系可知，在高溫條件下理論與試驗結果基本一致，但在低溫條件下，二者之間仍存在較大差異。

用布洛赫自旋波方法［13］研究低溫條件下磁化強度與溫度的關系。經自旋波方法處理后，系統的能量變化只與自旋有關，設晶體內原子總數為N，基態時自旋取向朝上，激發態時，可以出現自旋反向，反向自旋數為q，可能的自旋波數目為np，每個自旋波的能量均為β，對應不同反向自旋形成的自旋波矢Γn的自旋波總能量為

考慮外加磁場強度H作用下，當q個反向自旋出現后，系統的位能為

整個晶體在基態下的能量變化為

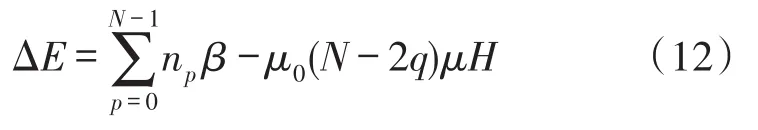
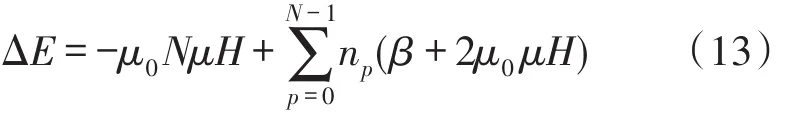
得到整個晶體的能量后，可知整個晶體的配分函數［13］

由式（13）、式（14）可得

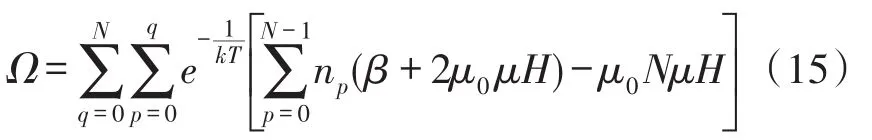
式中，k為波爾茲曼常數。磁化強度可表示為

由式（15）、式（16）可得

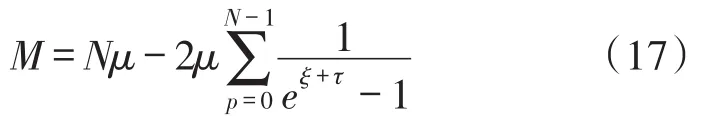
其中，

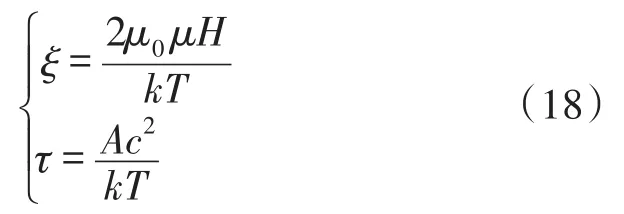
式中，T為溫度，A為交換積分，c為晶格常數。

將式（17）對溫度求偏微分可得磁化強度隨溫度的變化率為

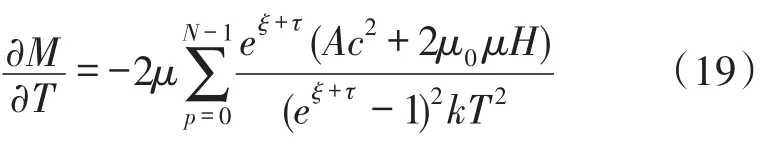
如將式（17）對外加磁場強度求偏微分可得磁化強度隨外加磁場強度的變化率，即磁化率為

由式（17）、式（19）、式（20）可知，磁化強度和磁化率與溫度呈復雜非線性函數關系，且受溫度、外加磁場和鐵磁材料的晶體結構等多重因素影響。

分析可知，外斯分子場理論在高溫時與試驗結果有較好的吻合度，而布洛赫自旋波理論在溫度很低時與試驗結果基本符合，但是，在一般的工作溫度范圍內，兩種理論方法仍然不能精確地描述磁化強度與溫度的相互關系。

2.2差動式補償技術

溫度對鐵磁材料的磁化強度影響很大，其影響規律和理論模型十分復雜。為有效消除溫度影響產生的誤差，提出了一種基于并行裝配的補償勵磁傳感器結構，通過采用差分技術，實現溫度全程的差動式補償。

①溫度補償結構

在旁路式傳感器基礎上并行裝配一個結構、參數完全相同的補償勵磁傳感器，分別與工作鋼纜索和補償鋼纜索形成閉環系統。由工作鋼纜索構成的索力傳感器受到索力和溫度的雙重作用，其輸出信號VSW包含索力、溫度相關信息，而補償鋼纜索構成的補償傳感器只受到溫度的影響，其輸出信號VSC只與溫度波動信息有關，兩部分信號同時傳輸給后置信號放大器，運用共享調理模塊的差分方法，實現差動式溫度的有效補償。溫度補償的磁路結構如圖3所示。

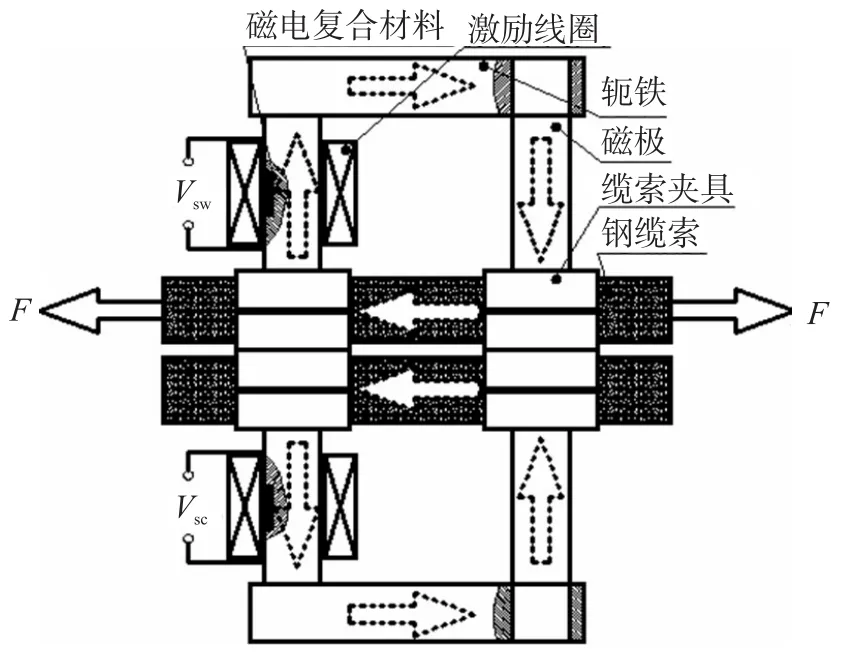
圖3　差動式溫度補償結構

②差分補償原理

由于勵磁電流是脈沖恒流電流，因此外加磁場強度是恒定的，VSW和VSC是感應拉力和溫度變化引起回路磁通發生改變而產生的誘導電壓，一般情況下電壓信號比較微弱，需要用信號調理模塊對原始輸出電壓VSW和VSC進行信號預處理，然后再進行差分運算。VSW和VSC兩路輸出電壓信號采用同一調理模塊，實現全溫度范圍內的有效補償。運用差分技術［14］所設計的差動信號處理電路如圖4所示。

圖4　差動信號處理電路

SC為溫度補償傳感器，SW為索力傳感器，S1，S2，S3，S4為切換開關，K為信號調理模塊，S為脈沖信號發生器，R為電阻，Q為信號轉換開關，為采樣保持電路，A為差動運算放大器。差動補償技術的控制與運算過程分以下兩種情況：

首先，當S為高電平時，Q的端口1為高電平，2為低電平，S2和S4接通，采樣電路工作。溫度補償傳感器SC輸出的電壓VSC經S2輸入到信號調理模塊K，處理后再經S4輸入到采樣保持器中，其輸出電位為差動運算放大器A的D端電位VD，可表示為

式中，Vt1為溫度為t1時SC輸出的電壓，V1為信號調理模塊誤差電壓。

式中，VC0為SC在溫度t0，SC為空載時的輸出電壓，ε為傳感器的輸出電壓溫度系數。

將式（21）代入式（22），則有

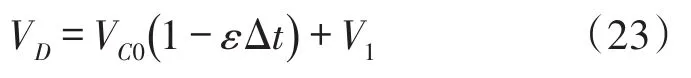
其次，當S為低電平時，Q的端口1為低電平，2為高電平，S1和S3接通。索力傳感器SW的輸出電壓VSW經S1輸入到信號調理模塊K，處理后再經S3輸入到差動運算放大器A的G端，其電位VG為

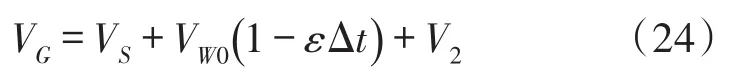
式中，VS為索力產生的輸出電壓，VW0為SW在溫度t0，SW為空載時的輸出電壓，V2為信號調理模塊誤差電壓。

因此，差動運算放大器的輸出電壓V為

式中，K為放大倍數。將式（23）、式（24）代入式（25），由于兩脈沖之間時間很短，有V1=V2，則有

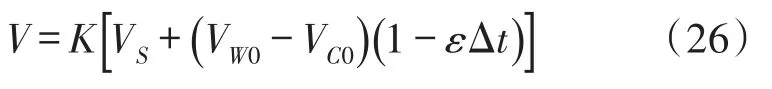
由于兩個傳感器的結構、參數完全一致，有VC0=VW0，式（26）變為

由此可見，信號處理電路的輸出電壓V只與索力引起的輸出電壓VS有關，與溫度無關，從而實現了全溫度范圍內的完全補償。

3　溫度與拉力試驗

3.1試驗目的與條件

試驗目的：獲得傳感器輸出電壓的溫度影響曲線，分析在復雜溫度變化時對傳感器輸出電壓的影響規律；以及驗證差動式溫度補償技術在變載荷作用下磁路結構與信號處理電路的補償效果。

試驗條件：選擇直徑12 mm的鋼纜索作為試驗對象。激勵線圈匝數500，線徑0.6 mm，激勵電流I= 0.8 A，脈沖電流頻率100 Hz，驅動磁場強度HAC≤15 kA/m。傳感器在-30℃～80℃環境溫度范圍內，在空載情況下，每間隔10℃選取一個測試點，并恒溫半小時，保證其溫度場均勻性。在升溫、降溫條件下，重復進行漸變、突變過程的傳感器性能穩定性測試試驗，并選取每個測試點的平均值進行試驗比較分析。

3.2溫度影響試驗

鋼纜索在空載情況下，旁路式索力傳感器結構在升、降溫過程中的誘導電壓與溫度的關系曲線如圖5、圖6所示。

圖5　升溫過程變化曲線

圖6　降溫過程變化曲線

升溫時，在-10℃～50℃之間，誘導電壓與溫度基本呈線性關系，在50℃～70℃之間，溫度曲線在60℃時發生畸變，出現與前面截然不同的變化趨勢，重復多次試驗得到類似的結果。降溫時，在-10℃～20℃之間，誘導電壓與溫度基本呈線性關系，溫度從70℃下降到20℃時，溫度曲線在70℃、50℃、30℃三處發生畸變，重復多次試驗其結果相同。試驗表明，誘導電壓與溫度之間呈復雜的非線性函數關系。

3.3變載下溫度補償試驗

①空載試驗

鋼纜索在空載情況下，差動式傳感器結構中誘導電壓與溫度的關系曲線如圖7所示。在-30℃～+80℃溫度范圍內，無論進行升溫或者降溫試驗，最大的重復誤差小于0.3%，達到了溫度誤差的全程自動有效補償。

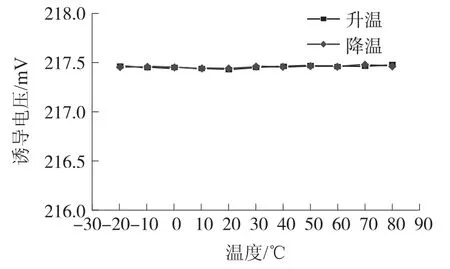
圖7　空載過程電壓與溫度曲線

②變載試驗

鋼纜索在4 kN、10 kN和16 kN變載情況下，差動式傳感器結構中誘導電壓與溫度的關系曲線如圖8所示。在-30℃～+80℃溫度范圍內，進行多次升溫和降溫試驗，最大的重復誤差小于0.2%，同樣，實現了溫度誤差的全程自動有效補償。

圖8　不同載荷下電壓與溫度曲線

試驗表明，誘導電壓只與載荷大小有關，溫度對電壓信號測試結果的影響十分微小，產生的波動量小于1%，完全滿足了溫度誤差自動補償的目標。因此，在空載和不同載荷條件下，差動式傳感器結構對消除磁彈效應法溫度產生的檢測誤差，其效果是十分明顯的。

3.4差動式拉力試驗

在WDW-300拉伸試驗機上，鋼纜索受力范圍為0～20 kN，在實時變溫條件下，進行多次參數試驗，每次重復測試五組，每間隔2 kN選取一個測試點，并選取每個測試點的平均值進行試驗比較分析。將試驗測得的誘導電壓與施加在鋼纜索上拉力進行線性回歸擬合，其結果如圖9所示，五次試驗的線性相關系數分別為0.999 83、0.998 63、0.998 87、0.998 74、0.997 86，重復誤差在0.04%～0.30%。

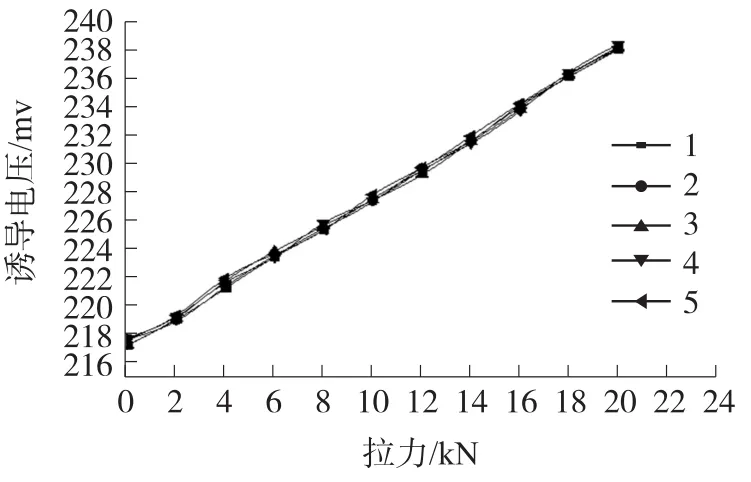
圖9　差動式拉力重復性試驗

4　結論

（1）溫度對誘導電壓的影響并非簡單的線性關系，在相同的條件下，升溫與降溫過程具有較大差別。實際工程中，溫度始終處于升溫與降溫交替過程，運用差動式結構補償方法，在-30℃～+80℃溫度之間，溫度對誘導電壓的影響微小，波動量小于1%。

（2）差動式索力傳感器在0～20 kN變載荷下可實現全溫度范圍內的自動補償，有效地消除了溫度對傳感器檢測精度的影響，解決了磁彈效應法的溫度補償技術難題，能滿足索力檢測實際要求。

（3）采用差動式索力傳感器檢測拉力，其線性擬合的相關系數達到0.99以上，檢測重復誤差可以控制在0.04%～0.30%之間，具有較高的索力檢測精度，以利于磁彈效應法的應用推廣。

［1］ Yang Bintang，Liu Qingwei，Zhang Ting，et al.Non-Contact Translation-Rotation Sensor Using Combined Effects of Magnetostriction and Piezoelectricity［C］//Sensors，2012，12：13829-13841.

［2］ 孫江波，趙紅華，趙作周.斜拉索索力測量方法的比較分析［J］.工業建筑，2011，4（增刊）：402-405.

［3］ Kvasnica B，Kundracik F.Fitting Experimental Anhysteretic Curves of Ferromagnetic Materials and Investigation of the Temperature and Tensile Stress［J］.Journal of Magnetism and Magnetic Materials，1996，162：43-49.

［4］ Ming L Wang，G Wang，Y Zhaol，et al.Application of EM Stress Sensors in Large Steel Cables，2003.

［5］ Zhao Y，Wang M L.Non-Destructive Condition Evaluation of Stress in Steel Cable Using Magneto-Elastic Technology［C］// Proc SPIE，2006，6178：617802.

［6］ Sumitro S.True-Stress Measurement of PC Steels by EM sensor［J］.J of Pre-Stressed Concrete Japan（Japan Prestressed Concrete Engineering Association），2001，43（6）：99-103.

［7］ 邵磊，馮志敏.基于旁路結構的磁彈效應索力傳感器研究［J］.傳感技術學報，2015，28（7）：997-1002.

［8］ 海振銀，高立波，李俊漾，等.柔性復合壓電薄膜的制備及其電導率研究［J］.傳感技術學報，2014，27（7）：861-865.

［9］ 張納.超磁致伸縮/壓電層狀磁電復合材料的磁電效應研究［D］.天津：河北工業大學，2011：23-71.

［10］Bozorth R M.Ferromagnetism［M］.Van Nostrand，Toronto，1951：63-95.

［11］Jiles D C，Atherton D L.Theory of Ferromagnetic Hysteresis［J］.J Magn Mater，1986：48-60.

［12］Duan Yuanfeng，Zhang Ru，Zhao Yang，et al.Steel Stress Monitoring Sensor Based on Elasto-Magnetic Effect and Using Magneto-Electric Laminated Composite［J］.American Institute of Physics，2012（4）：07E516-1-07E516-3.

［13］宛德福，馬興隆.磁性物理學［M］.北京：電子工業出版社，1999：188-199.

［14］吳鎮揚.數字信號處理［M］.北京：高等教育出版社，2004：99-167.

馮志敏（1960-），男，漢族，教授，主要從事機械設備狀態監測與故障診斷研究，fengzhimin@nbu.edu.cn；

邵磊（1989-），男，漢族，碩士研究生，主要研究方向為海洋工程故障診斷與機電控制，shaolei8905@163.com。

Differential Temperature Compensation and Experimental Studies of Magneto-Elastic Effect Cable Force Sensor*

FENG Zhimin*，SHAO Lei，CHEN Yuehua
（Maritime College of Ningbo University，Ningbo Zhejiang 315211，China）

On the basis of the study of cable force test method using bypass structure based on magneto-electric laminated composite，using the ferromagnetic molecular field theory and Bloch spin wave method，the function relation between magnetization and temperature is established to study the influence mechanism of temperature on test accuracy.The temperature compensation sensor with a parallel assembly magnetic circuit structure is proposed.Using the difference operation technology，a differential signal processing circuit with time sharing signal conditioning function is designed to realize the automatic compensation for the whole temperature range.Test shows：under the 0～20 kN variable load and in-30℃～+80℃temperature range，the influence of temperature fluctuation is less than 1%；measurement repeatability error is 0.04%～0.30%.It can solve the problem of temperature compensation effectively and meet the requirements of cable force test engineering.

cable force sensor；temperature compensation；differential technique；magneto-electric laminated composite；magnetization

TU502；TP212.6

A

1004-1699（2016）07-0984-06

項目來源：國家科學自然基金項目（51505237）；浙江省科技計劃項目（2013C31045）

2015-12-09修改日期：2016-03-15