A Robust Multiple Antenna Blind Spectrum Sensing Algorithm Based on Rank Criterion in Cognitive Radio*

ZHANG Jun，YANG Xi*，WANG Xiangming（.College of Information Science and Engineering，Jishou University，Jishou Hu'nan 46000，China；.Shanghai Stock Exchange Technology Co.，Ltd，Shanghai 000，China）

A Robust Multiple Antenna Blind Spectrum Sensing Algorithm Based on Rank Criterion in Cognitive Radio*

ZHANG Jun1，YANG Xi1*，WANG Xiangming2
（1.College of Information Science and Engineering，Jishou University，Jishou Hu'nan 416000，China；2.Shanghai Stock Exchange Technology Co.，Ltd，Shanghai 200120，China）

In the multiple antenna sensing scenarios，the sensing performance of the classical energy detection（ED）method shows the instability owing to the noise uncertainties phenomenon.Using the fact that the statistical covariance matrix of the multiantenna received signal is a rank-1 matrix，this paper presents a new spectrum sensing method based on the rank criterion.In the new algorithm，the sample covariance matrix of the received signal is firstly divided into an unknown ideal matrix and a perturbed matrix，and then the rank detection criterion is used to estimate the optimal dimension of the received signal space，and finally the estimated value is used to decide the channel state.Compared with the ED method，the proposed method is robust to noise uncertainty and belongs to blind detection.Specifically，the new algorithm does not need to use noise variance，the statistical characteristic of the primary user signal and the wireless channel to make a right decision.Simulation results verify the effectiveness of the proposed rank criterion based multiantenna spectrum sensing algorithm.

blind spectrum sensing algorithm；noise uncertainty；blind rank criterion detection（BRCD）；energy detection（ED）；the sample covariance matrix

EEACC:6140doi:10.3969/j.issn.1004-1699.2016.07.025

Cognitive radio is considered as one of the most promising solutions to deal with the conflict between the enormous spectrum demands and the scarcity of the radio spectrum resources［1-3］.It is well known that effective spectrum sensing algorithm is one of the fundamental and challenging tasks in cognitive radio.Classical spectrum sensing algorithms include cyclostationary detection（CD），energy detection（ED），and matched filtering（MF）.Among them，the ED method is widely used in spectrum sensing applications due to its simplicity and effectiveness［4-7］.However，the performance of the ED method and the ED-based cooperative schemes are degraded due to the noise uncertainty phenomenon，which is inevitable in practical sensing environment and eventually results in“SNR wall”problem［8］.In addition，ED is the optimal sensing scheme for detecting the zero mean independent and identically distributed received signal，but not for the correlated received signal［9］.Theoretical analysis has indicated that，to achieve the same detection performance，the required number of samples for ED neglecting the signal correlation is much larger than that of the sensing scheme fully exploiting the signal correlation.

To overcome shortcomings of the ED method，we introduce a new blind spectrum sensing method based on the rank criterion detection，which does not depend on the noise power and the prior information of primary user signal and wireless channel.Simulation results verify the effectiveness and superiority of the proposed algorithm.

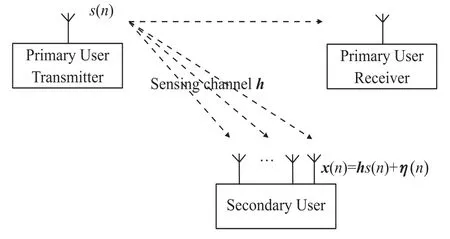
Fig.1　Rank criterion based multiantenna spectrum sensing model

The rest of the paper is organized as follows.In section 1，the multiantenna spectrum sensing system model is introduced.In section 2，the multiantenna spectrum sensing algorithm based on rank criterion is proposed.Simulation results are given in Section 3 and conclusions are drawn in section 4.

The notations are shown as follows.Vectors are column vectors denoted in lower case bold，e.g.x.Matrices are denoted by upper case bold，e.g.A.IQdenote the Q×Q identity matrix.The superscript“T”means transpose operator.det（A）is the determinant of A.E｛｝denotes expectation operator of a random variable.

1　System Model

A typical multiple antenna spectrum sensing scenarios is described in Fig.1［4］.Suppose that Q antennas are equipped at the secondary user andNsamples are obtained at each antenna.The Q×1 received signal vector and noise vector are respectively defined by

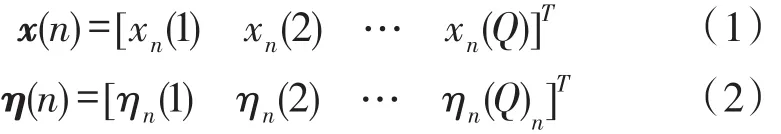
Noting that the received signal vector can be written as

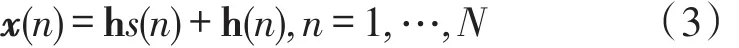
where theQ×1vectorh=［h1，h2，…，hQ］expresses the flat fading channel gain between the primary user and the M antennas.The binary hypothesis testing problem for spectrum sensing can then be represented as

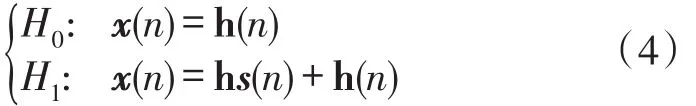
where H0indicates the primary signal does not appear，and H1indicates the primary user signal exists.Here，the primary user signal samples are assumed to be statistical independent Gaussian random variables with zero mean and varianceThis assumption is valid for an orthogonal frequency division multiplexing（OFDM）signal in which each carrier is modulated by independent data streams.In addition，the noise sample vectorη（n）are zero mean white Gaussian process with covariance matrixWithout loss of generality，the primary signal and the noise are assumed to be statistically independent.Therefore，the statistical covariance matrix of the received signal under hypothesis H1can be written as

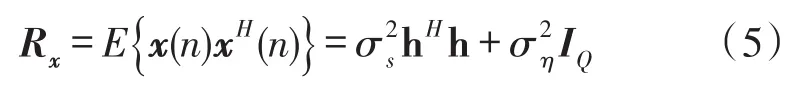
Using the fact that hhHisrank-1 matrix，we can conclude that

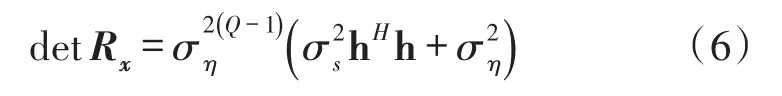
Letρ1≥ρ2≥…≥ρQdenote the eigenvalues of the statistical covariance matrix Rx.According to（6），the eigenvalues of Rxunder hypothesis H1can be shown as

Noting that all eigenvalues of the statistical covari-ance matrix are equal to the noise power.Combining（7）and（8），the binary hypothesis model for multiantenna spectrum sensing can then be rewritten as

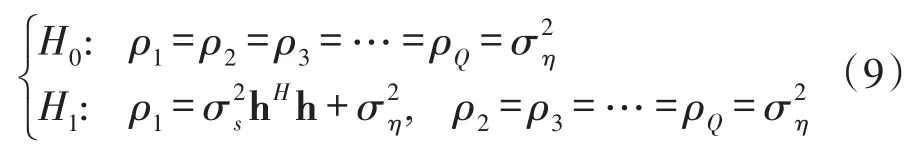
From（9），it is not difficult to show that the multiantenna spectrum sensing problem is equivalent to confirm the existence and uniqueness of the maximum eigenvalue of the statistical covariance matrix.If the largest eigenvalue exists and is unique，we can conclude that the primary signal appears；if all eigenvalues are equal，then the primary signal does not appear and the spectrum hole exists.Because the statistical covariance matrix of the received signal is usually unknown，the statistical covariance matrix is approximated by the sample covariance matrix（SCM）based on the received signal vectors in practical applications which is defined as

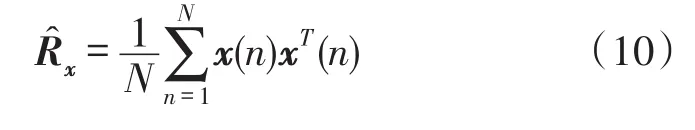
2　Proposed Rank Criterion Based Multiple Antenna Spectrum Sensing Algorithm

To overcome the limitations of the sensing algorithm based on the ED method，this paper introduces the rank detection criterion，which has been widely used to effectively estimated the channel order［10］，to deal with the multiple antenna spectrum sensing problem.The main idea of this method is summarized as follows：Firstly，based on the idea of subspace decomposition，the received signal space is decomposed to the sum of ideal signal subspace and noise subspace，which are orthogonal to each other and are spanned by the eigenvectors corresponding to the sample covariance matrix.Secondly，by introducing a perturbation to the received signal space to generate a perturbed signal subspace，we then measure the space distance between the estimated signal subspace and the perturbed signal subspace.Finally，according to the rank detection criterion function，we determine the optimal rank estimation of the sample covariance matrix and decide the state of the authorized spectrum.

2.1Principle of the Proposed Algorithm Based on Rank Criterion

As for the proposed rank criterion based multiantenna spectrum sensing algorithm，the sample covariance matrix is firstly decomposed into the sum of an ideal matrix Ridealand a perturbation matrix Rpertur

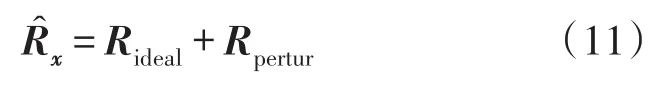
where Ridealis a rank-q matrix associates with the significant part of the primary users signal，and Rperturis mainly composed of the influence including of white or colored additive channel noise and the numerical error caused by the inexact estimation to the sample covariance matrix.The spectral decomposition of the sample covariance matrix is denoted as

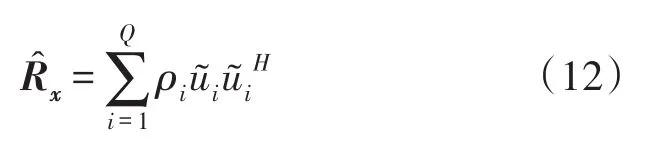
where the eigenvalues ρi（i=1，2，…，Q）are sorted in descending order.The estimated signal subspace φsis spanned by the feature vectors corresponding to q largest eigenvalues according to（12），and noise subspace φeis spanned by the feature vectors corresponding to the rest Q-q smallest eigenvalues.Here，the estimated signal matrix is defined as

The ideal signal subspace is an unknown q-dimensional subspace spanned by the columns of Rideal.If φsis used to approximate the ideal signal subspace，we can then conclude a 2-norm lower bounds of matrix Rpertur［10］

From（14），we known that the ideal signal subspace and the estimated signal subspace are related through Rpertur.Using M to denote some perturbation matrix with minimum 2-norm，that is

When φsis insensitive to M，it is reasonable to consider that φsis close to the unknown ideal signal subspace；otherwise the two subspaces may be far away from each other［11］.In other words，the rank q makes the estimated matrix corresponding to Ridealbe insensitive to the perturbation matrix M.Now，we consider the problem that the sample covariance matrix is perturbed by the perturbation matrix M，i.e.，

and denoting the spectral decomposition of ψ as

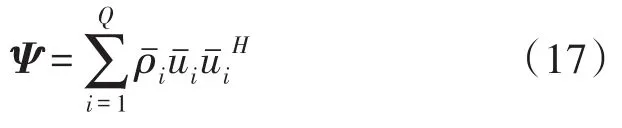
where the eigenvalues are sorted in descending order.Then the perturbed signal subspace φs_perturis spanned by the feature vectors corresponding to q largest eigenvalues of ψ.According to the matrix perturbation theory，the distance between φsand φs_perturcan be defined as the sine of their canonical angles.Invoking the results of［10］，the upper bound of the distance measure can be written as

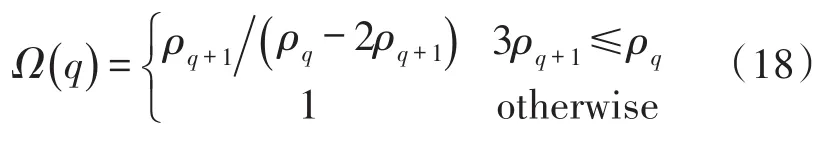
Formula（18）implies that the sensitivity of the estimated signal subspace φsto M is governed by the separation of the eigenvalues ρqand ρq+1.IfΩ（q）?1，then φsis insensitive to the perturbation matrix M.At this time，we can consider that φsis close to the ideal signal subspace.Therefore，the optimal rank estimation is obtained through minimizing（18）as follows

In multiple antenna spectrum sensing scenarios depicted in Fig.1，as analyzed in Section 1，the rank of Ridealshould equals to 1 under H1，which means.On the other hand，Ridealequals to zero matrix and so the rank of it is zero，which meansTherefore，combing（18）and（19），the decision rule for the proposed algorithm based on rank criterion can be rewritten as

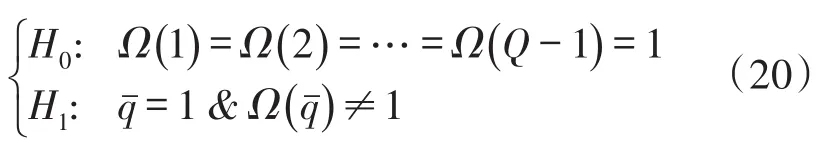
2.2Sensing Steps of the Proposed Algorithm Based on Rank Criterion

From（20），it can be seen that the decision rule only depends on the eigenvalues of the sample covariance matrix.Therefore，compared with the ED method，the proposed multiantenna spectrum sensing algorithm based on rank criterion is robust to noise uncertainty and belongs to blind detection.Specifically，the new algorithm does not need to use noise variance，the statistical characteristic of the primary user signal and the wireless channel to make a right decision.From above analysis，the algorithm process can be summarized as follows

Step 1Compute the sample covariance matrix using（10）；

Step 2Perform the eigenvalue decomposition for the sample covariance matrix according to（12），andobtainQeigenvaluesindescendingorder ρ1≥ρ2≥…≥ρQ；

Step 3Compute the distance upper bound（q=1，2，…，Q）between the estimated signal subspace and the perturbed signal subspace according to（18）；

Step 4Decide the authorized channel state：estimate the optimal rank using（19）.If，then the channel is occupied；if，then the channel is vacant.

Correspondingly，the realization of the proposed algorithm based on rank criterion is described in Fig.2.

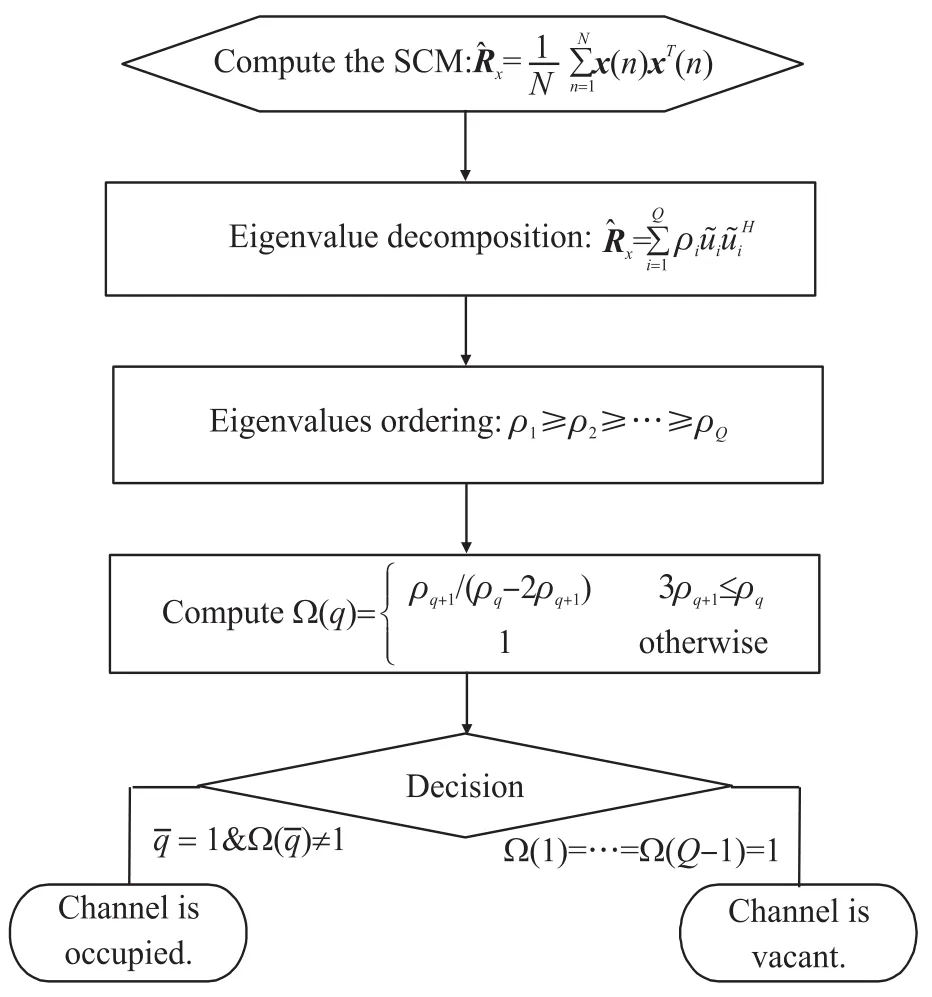
Fig.2　Implementation flowchart of the new algorithm

3　Numerical Simulation and Analysis

We consider a multiantenna sensing scenario as in Fig.1.The independent binary phase shift keying（BPSK）signals are transmitted by the primary user.In a realistic environment，the accurate noise variance is not available due to noise uncertainty.To evaluate the real sensing performance of the ED and the proposed BRCD methods，an estimation errorδ［dB］followed a uniform distribution in［-A，A］is added in noise variance［12］，where A denotes the maximum value of noise uncertainty.The real noise variancein each simulation is

In the following，ED-x dB and BRCD-x dB denote the ED and the BRCD methods with x dB noise uncertainties，respectively.In Table 1 and Table 2，we investigate the actual false alarm performances of the ED and BRCD methods by setting different values of predefined false alarm probabilities（PFA）and the noise uncertainty level.It can be seen that the proposed method perform excellent false alarm performance，however，the actual false alarm probabilities for the ED method far exceeds the predefined values due to noise uncertainty.Combining Table 1and Table 2，we observe that all actual false alarm probabilities of the ED method are greater than 0.3 for all predefined false alarm probabilities（PFA=0.01，0.05，0.1）.This means that the detection performance of ED method is very unreliable in practical situations when the noise uncertainty phenomenon exists.Meanwhile，a high false alarm probability means that the reduction of the chance for the cognitive users to use the idle spectrum in CR.That is to say，compared with the BRCD method，the ED method dramatically reduces the spectrum efficiency of the cognitive users due to the existence of noise uncertainty.

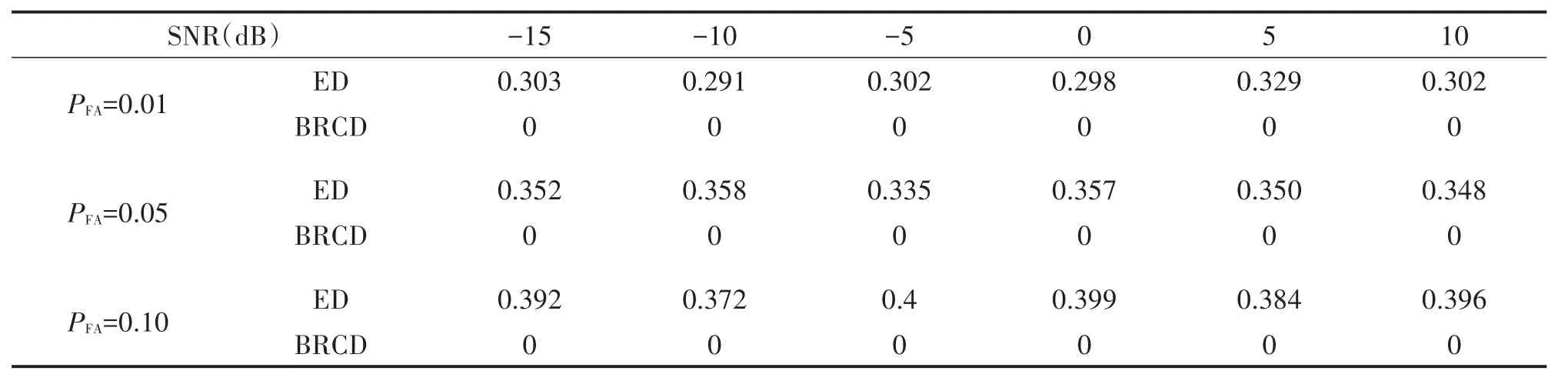
Table 1　Actual probabilities of false alarm comparison between BRCD and ED when noise uncertainty is 1 dB

Table 2　Actual probabilities of false alarm comparison between BRCD and ED when noise uncertainty is 2 dB

The actual detection performances of the ED and BRCD are evaluated in Fig.3.Firstly，we observe that with the increasing of predefined false alarm probabilities and noise uncertainty，the detection probabilities of the BRCD method keep almost the same.In contrast，the detection probabilities of the ED method have larger fluctuation in all simulation scenarios，which indicates that the BRCD method is more robust to noise uncertainty.Secondly，we also see that the BRCD method performs better detection performance in the relatively high signal-to-noise ratio（SNR）region，while shows relatively lower probability than the ED method in the low SNR region.However，it is also worth pointing out that the actual high false alarm probability of the ED method increases its detection probability in all SNR regions and leads to an unreliable detection result.

The detection performances of the BRCD method for different sample sizes are presented in Fig.4.Here，we fix P=12，and vary the sample size from N=100 to N=1 500.With the increase of sample size the detection probability of the BRCD method increases yet.For example，the detection probability increases from 90% to 100%when the sample size N increases from 100 to 1 500，while SNR is set to-9 dB.

When antenna number changes，the sensing performance of the new algorithm is investigated in Fig.5. As expected，we observe that the sensing performance of the proposed BRCD algorithm benefits from increasing antenna number.For example，when SNR equals-9 dB，with increasing the antennas number P from 2 to 8，the detection probabilities increase from 85%to 97%.

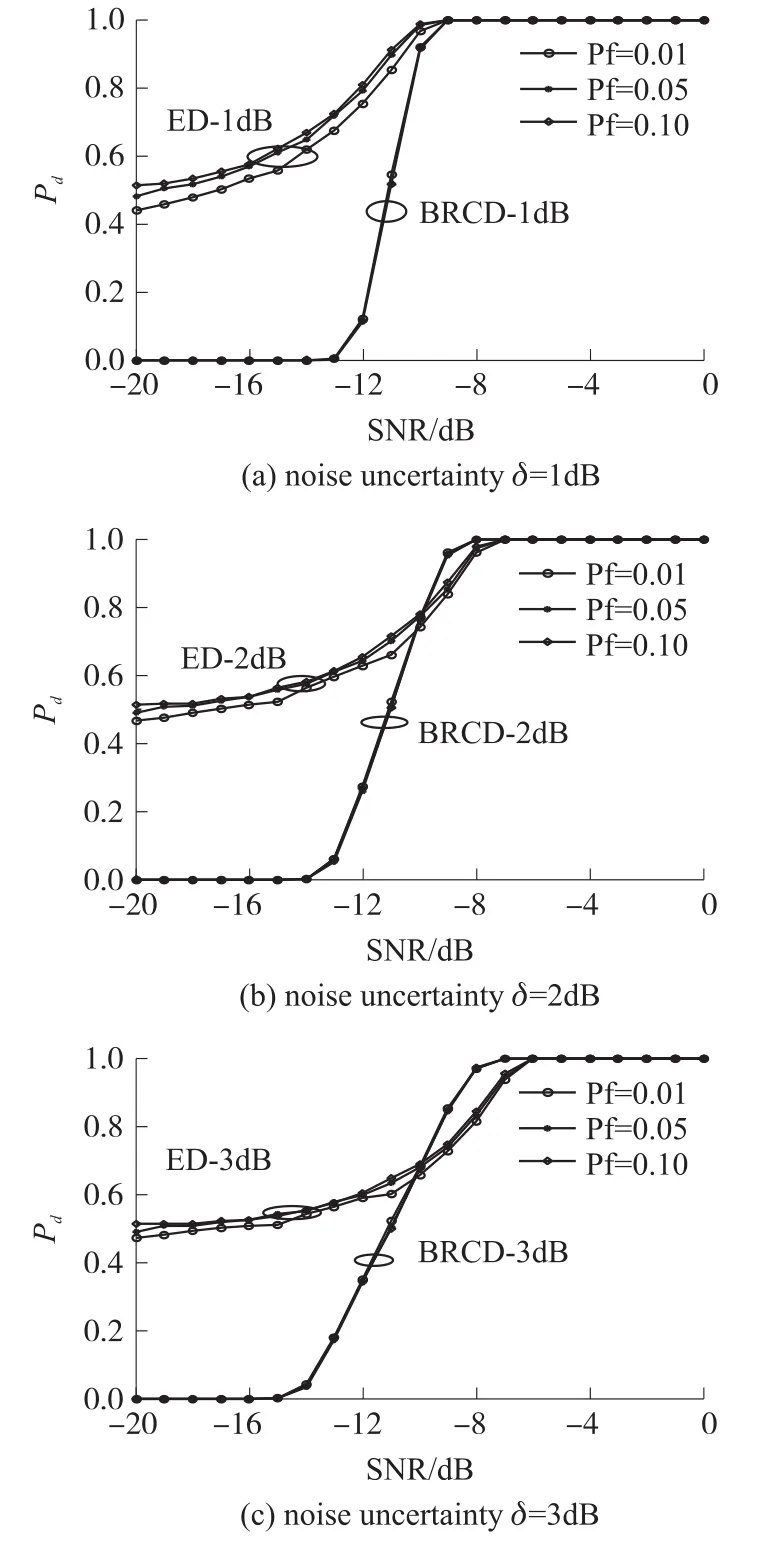
Fig.3　Probabilities of detection comparison between BSED and ED when different noise uncertainties are given（N=200，P=12）

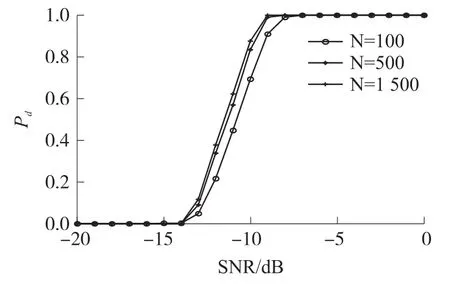
Fig.4　Sensing performance of the BRCD for different sample sizes（2 dB noise uncertainty）

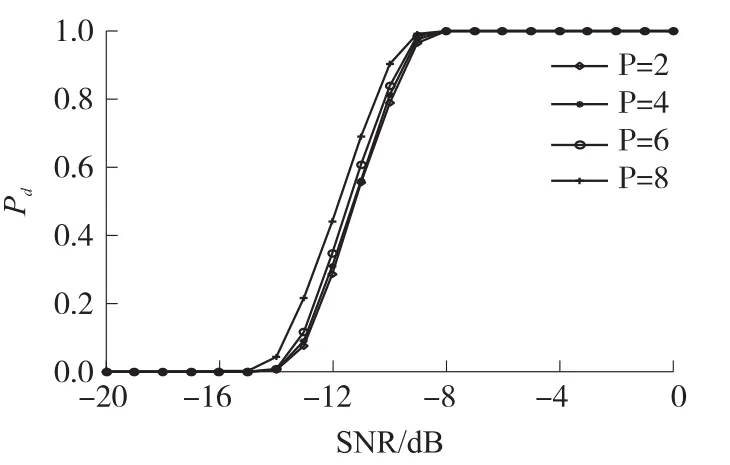
Fig.5　Sensing performance of the BRCD for different numbers of antennas（N=200，2dB noise uncertainty）

4　Conclusion

This paper introduces a new blind spectrum sensing algorithm based on the rank criterion，which does not need to set the false alarm probability and compute the decision threshold.In the sensing scenarios without any information about the noise variance，the primary signal and the wireless channel，compared with the classical ED method，the BRCD method is more robust to noise uncertainty.Simulation results verify the effectiveness of the proposed sensing method.

［1］ Akhtar A M，Wang X，Hanzo L.Synergistic Spectrum Sharing in 5G HetNets：A Harmonized SDN-Enabled Approach［J］.IEEE Communications Magazine，2016，54（1）：40-47.

［2］ Wei M，Lian Q S.The Wideband Spectrum Covariance Sensing Algorithm Based on Compressed Sensing［J］.Chinese Journal of Sensors and Actuators，2011，24（7）：1022-1026.

［3］ Zhou F，Beaulieu N C，Li Z，et al.Energy-Efficient Optimal Power Allocation for Fading Cognitive Radio Channels：Ergodic Capacity，Outage Capacity，and Minimum-Rate Capacity［J］.IEEE Communications Magazine，2016，15（4）：2741-2755.

［4］ Abbas Taherpour，Masoumeh Nasiri-Kenari，Saeed Gazor.Multple Antenna Spectrum Sensing in Cognitive Radios［J］.IEEE Transactions on Wireless Communications，2010，9（2）：814-823.

［5］ Pan C，Wang J，Zhang W，et al.Power Minimization in Multi-Band Multi-Antenna Cognitive Radio Networks［J］.IEEE Trans. Wireless Commun.，2014，13（9），pp.5056-5069.

［6］ Quan Z，Cui S，Sayed A H.Optimal Linear Cooperation for Spectrum Sensing in Cognitive Radio Networks［J］.IEEE J Select Topics Signal Processing，2008，2（1）：28-40.

［7］ Qing H B，Liu Y N，Xie G.Smart Antennas Aided Wideband Detection for Spectrum Sensing in Cognitive Radio Networks［J］. Electronics Letters，2014，50（7）：490-492.

［8］ Tandra R，Sahai A.SNR Walls for Signal Detection［J］.IEEE J Select Topics in Signal Processing，2008，2（1）：4-17.

［9］ Lei K J，Yang X，Peng S L，et al.Eigenvalues Detection Based Spectrum Sensing Algorithm for Cognitive Radio［J］.Chinese Journal of Sensors and Actuators，2012，25（6）：771-777.

［10］Liavas A P，Regalia P A，Delmas J P.Blind Channel Approximation：Effective Channel Order Determination［J］.IEEE Transactions on Signal Processing［J］.1999，47（12）：3336-3344.

［11］Haykin Simon.Adaptive Filter Theory（5th Edition）［M］.USA：Prentice Hall，2013.

［12］Zeng Y H，Liang Y C.Spectrum-Sensing Algorithms for Cognitive Radio Based on Statistical Covariances［J］.IEEE Transactions on Vehicular Technology，2009，58（4）：1804-1815.

Zhang Jun（1979-），is a graduate student in the college of the information science and engineering，Jishou University. His current research interests include statistical signal processing theory and it's applications in cognitive radio；

Yang Xi（1978-）is an associate professor in the college of the information science and engineering，Jishou University，obtained doctor's degree in communication and infomation system from Southeast University in 2014.His current research interestsincludewirelesscommunications theory and applications，statistical signal processing and cognitive radio.E-mail：ynkej@163.com；

Wang Xiangming（1964-）is manager of Shanghai Stock Exchange Technology Co.，Ltd.（SSE Tech），obtained master's degree in communication and electronic system from Southeast University in 1988，has been engaging in communication network for SSE Tech（The former name is Shanghai StockCommunicationCo.，Ltd.）since2000.

認知無線電中一種基于秩準則的魯棒多天線盲頻譜感知算法*

張軍1，楊喜1*，王向明2
（1.吉首大學信息科學與工程學院，湖南吉首416000；2.上交所技術有限責任公司，上海200120）

在多天線感知場景中，噪聲不確定的存在使得經典的能量檢測算法的感知性能表現出不穩定性。基于多天線接收信號的統計協方差矩陣為秩-1矩陣這一事實，提出一種基于秩準則的頻譜感知方法。該方法首先將取樣協方差矩陣分解為具有未知秩的理想信號矩陣和噪聲擾動矩陣之和，然后采用秩檢測準則估計接收信號子空間的最佳維數，最后利用該值判斷信道的狀態。與經典的能量檢測方法相比，新方法對噪聲不確定性具有良好的魯棒性，且屬于全盲檢測方法。具體而言，新方法在感知判決過程中，無需事先知道噪聲方差以及主用戶信號和無線信道的統計特征。仿真結果驗證了基于秩準則的多天線頻譜感知算法的有效性。

盲頻譜感知算法；噪聲不確定性；盲秩準則檢測；能量檢測；取樣協方差矩陣

TN92

A

1004-1699（2016）07-1102-07

2016-05-25修改日期：2016-06-14

項目來源：國家自然科學基金項目（61362018，61102089）；湖南省科技計劃項目（2015GK3032）；中央高校基本科研業務費專項資金項目；江蘇省博士后科研計劃項目（1402041B）