多跳頻信號頻率跟蹤與二維波達方向實時估計算法

張東偉 郭 英 張坤峰 齊子森 韓立峰 尚耀波

?

多跳頻信號頻率跟蹤與二維波達方向實時估計算法

張東偉*①②郭 英②張坤峰②齊子森②韓立峰①尚耀波①

①(空軍工程大學裝備發展與運用研究中心 西安 710051)②(空軍工程大學信息與導航學院 西安 710077 )

為了實時提取跳頻(FH)通信參數以及為通信對抗提供所需信息，該文提出一種多跳頻信號頻率跟蹤和2維波達方向實時估計算法。首先建立跳頻信號的L型陣列接收數據模型，并推導證明了自回歸滑動平均(ARMA)模型對L型陣列數據的適用性，然后采用粒子濾波思想對陣列流型矩陣和頻率進行實時估計。再基于頻率估計值建立ARMA模型實時檢測跳時刻，并結合流型矩陣估計值實現無需參數配對的2維波達方向(2D-DOA)準確估計。新方法通過設計合理的粒子生成以及權值更新方式，使流型矩陣與頻率估計值能夠迅速收斂至穩定狀態。最后蒙特卡羅仿真結果驗證了該算法的有效性。

信號處理；跳頻；頻率估計；波達方向；粒子濾波；自回歸滑動平均模型

1 引言

跳頻(Frequency Hopping, FH)通信具有優越的抗干擾、抗截獲和多址組網等能力，已逐漸成為軍事通信的主導技術，并在越來越多的信息系統中得到廣泛應用[1]。FH信號跟蹤和參數估計一直是通信偵察和通信對抗等領域的重要研究內容。

針對FH信號的實時估計問題，文獻[8]最早提出了一種基于粒子濾波的單/多通道FH信號頻率跟蹤方法。文獻[9]在文獻[8]基礎上建立了FH信號的相位統計模型，在單通道時取得了更好的跟蹤性能。但文獻[8,9]所提方法僅能處理一個信號，且在多通道時未能給出DOA信息，限制了其應用范圍。文獻[10]提出了一種基于時域自回歸滑動平均(Auto Regressive Moving Average, ARMA)模型的跳時刻實時檢測方法，首次實現了對多個FH信號的頻率跟蹤，但該方法的信噪比適應能力較弱。文獻[11]將粒子濾波思想與ARMA模型法相結合，提高了文獻[10]的信噪比適應能力，同時可獲取DOA信息。文獻[12]采用貝葉斯稀疏學習實現跳頻跟蹤，其信噪比適應能力略優于文獻[10]，但進行跟蹤時所需積累的樣本數多于文獻[10]和文獻[11]，且計算復雜度較高。

綜上可知，目前可同時跟蹤多個FH信號并能獲取DOA信息的方法較少，且尚未見到能實時估計FH信號2維波達方向(2D-DOA)的成果報道。而2D-DOA對FH網臺分選、信號識別和干擾等任務均具重要作用。針對該問題，本文在文獻[11]基礎上，利用兩個正交布置的均勻線陣(ULA)構造L型陣列，提出一種多FH信號頻率跟蹤和2D-DOA實時估計算法，并通過設計更為合理的粒子采樣和權值更新方式，提高了文獻[11]的頻率跟蹤性能(跳時刻檢測概率和頻率估計精度)。所提算法對同步、異步網臺都能適應，且在估計2D-DOA時無需參數配對。

2 陣列模型與問題描述

陣列結構如圖1，假定L陣交點為坐標原點，每邊是陣元間距分別為,的元ULA，兩ULA分別與+軸和+軸重合(記為ULA1, ULA2)。

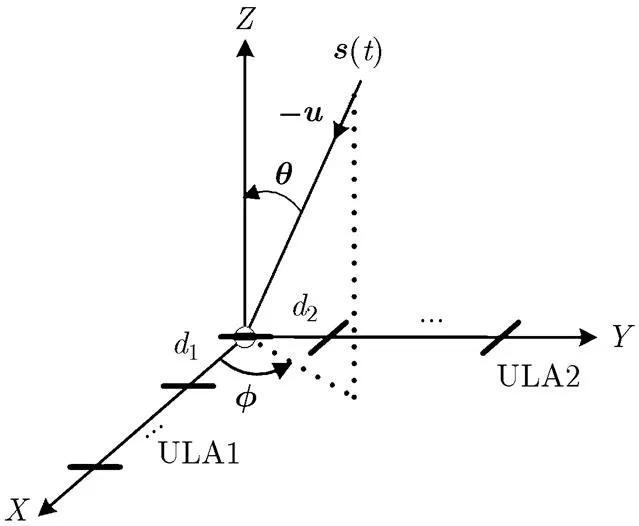
圖1 L型陣列結構

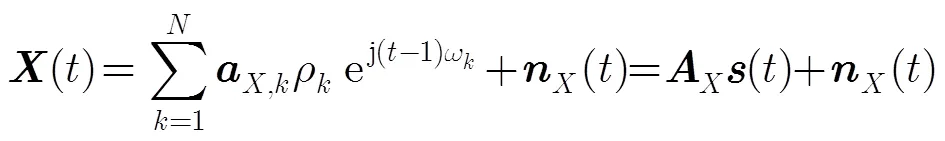
(2)

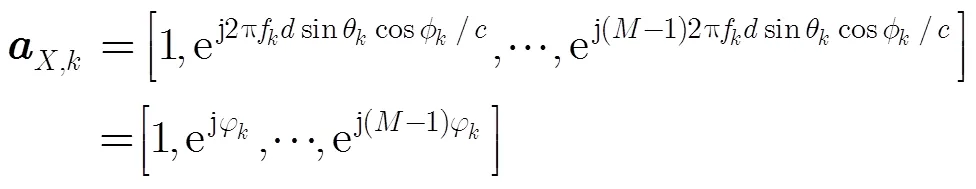
(4)

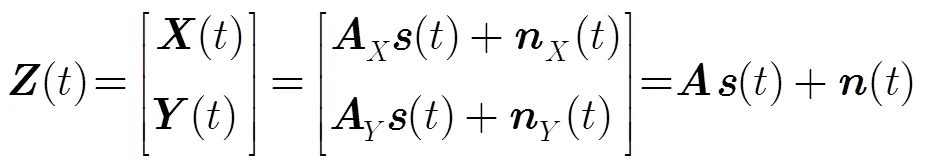
3 基于ARMA模型的跳時刻實時檢測

(7)

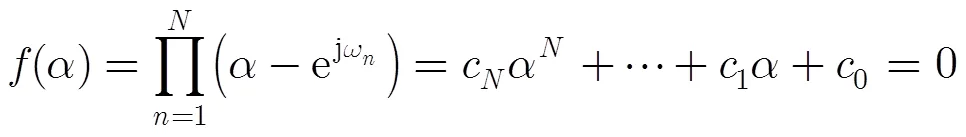
(9)

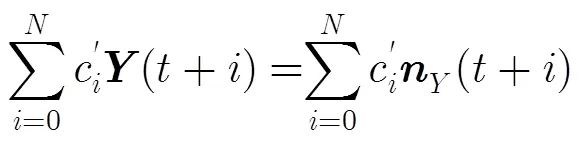
(11)

即L型陣列仍滿足ARMA模型。

假設各通道及各時刻的噪聲均相互獨立，服從均值為0，方差為的高斯分布，即，則式(11)的分布函數為

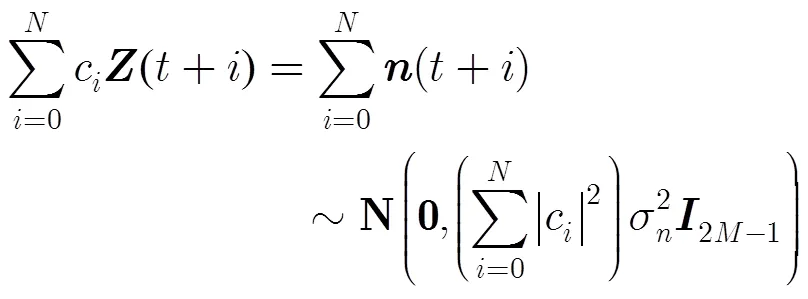
(13)

(14)

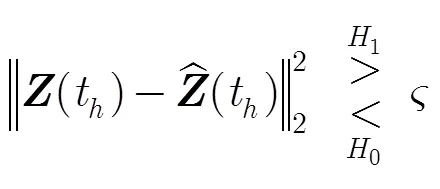
4 頻率與2D-DOA實時估計以及ARMA模型建立

對于偵察方，利用快拍數據僅有可能得到陣列對各信號的SPSF。文獻[11]引入粒子濾波[13]估計SPSF，但設計的粒子采樣方法未充分利用陣列信息，導致需經多次粒子更新才能收斂至穩定估計值，故在信噪比較低或跳周期較短時，其性能迅速下降。本節提出一種新的采用粒子濾波的SPSF估計方法。

4.1空間相移因子估計

(1)空間相移因子的后驗概率密度形式：以ULA1為例，未發生跳頻時，假設已采集到組快拍，則這組樣本服從獨立高斯分布，即

(17)

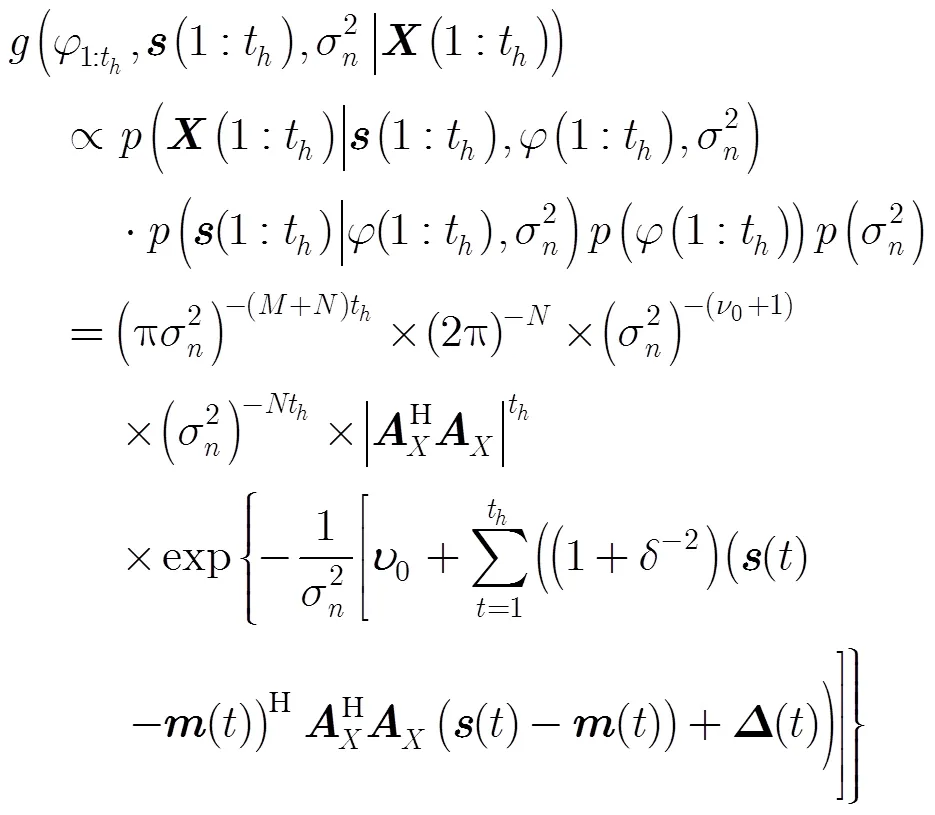
(19)

(2)空間相移因子的序貫估計

步驟3 SPSF估計。對粒子加權平均求得SPSF；

步驟4 重采樣。根據需要，對粒子進行重采樣；

我說，李書記把金枝嫁給我，那是我的福氣，婚姻大事怎么能簡單草率，我就是砸鍋賣鐵也得把事情操辦好，不能委屈了金枝。看著李老黑連連點頭，我進一步提出了要求。李書記不要把金枝鎖在屋里了，一個人的思想轉變總要有個過程不是，這幾天我會常過來跟她交流交流，溝通溝通思想，你看行不行？

式中，

(23)

(24)

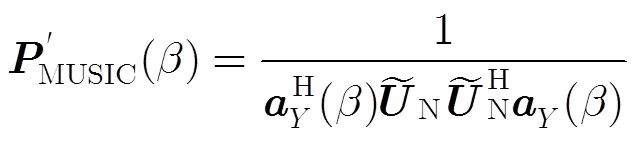
(27)

經過以上分析可見，相比于文獻[11]，本文采取的粒子生成方法充分利用了陣列信息，使得初始粒子更加接近SPSF真實值，利于后續粒子更新環節SPSF估計值迅速收斂至穩定狀態。

(b)粒子更新與空間相移因子估計：假設時刻粒子狀態為,，當接收到時刻快拍后，由于其與該FRT內所積累的歷史樣本具有相同參數，故只需在這組粒子上附加隨機高斯擾動(為擾動方差)以補償參數估計值可能存在的誤差，即

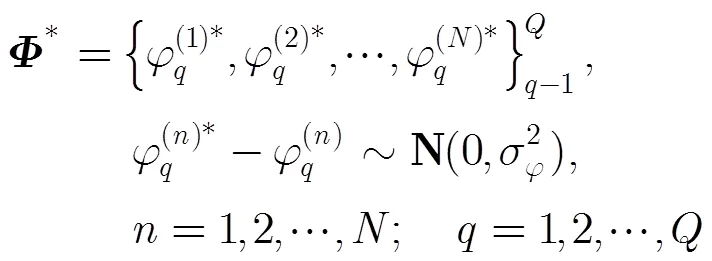
(29)

(31)

4.2頻率、2D-DOA估計以及ARMA模型建立

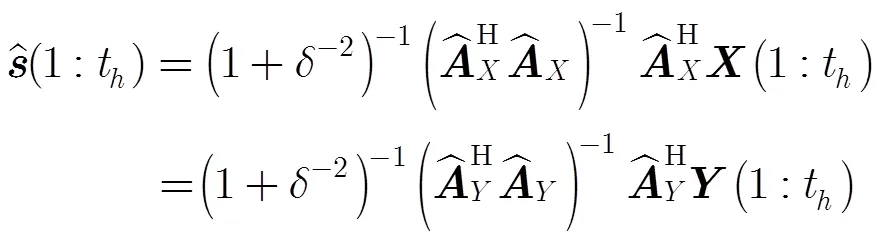
同時，相鄰時刻波形之間滿足

(34)

因此各信號頻率估計值為

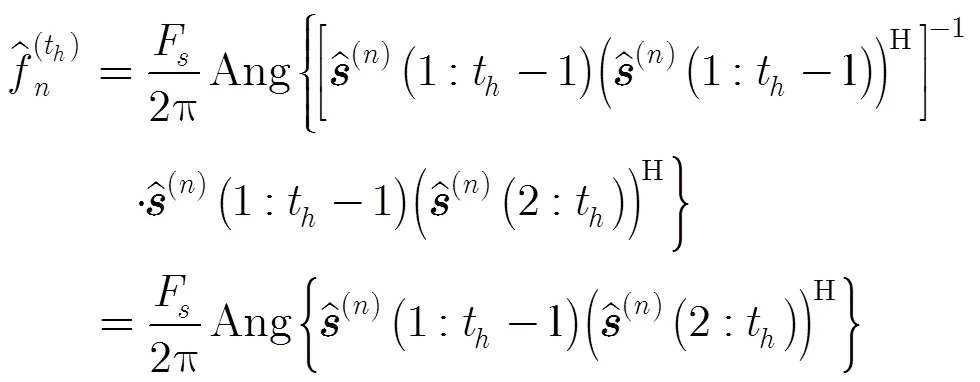
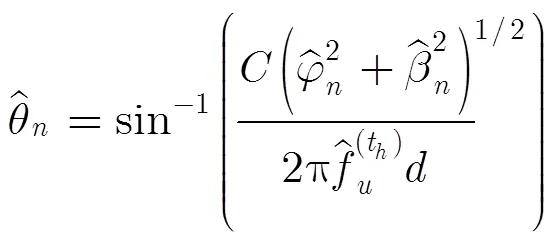
(38)

由式(37)、式(38)可見，俯仰角和方位角自動配對。

5 算法流程與運算復雜度分析

(1)算法流程總結：

步驟1 分別利用ULA1, ULA2在初始時刻的快拍數據構造各自的Toeplitz矩陣和，根據式(24)~式(27)生成兩組(每組個)維粒子；

步驟2 每接收一組新的快拍，分別(并行)對兩組粒子及其權值進行更新，并計算SPSF估計值。

(a)依據式(28)生成新粒子；

(b)由式(29)計算新粒子接收概率；

(c)由式(19)結合式(30)~式(32)計算更新后各粒子的歸一化權值并估計各信號的SPSF；

步驟3 利用SPSF估計值恢復流型矩陣，根據式(33)~式(35)估計頻率，并與SPSF估計值進行配對；

步驟5 通過式(13)和式(15)進行跳頻檢測。

(a)若未檢測到頻率跳變，回到步驟2；

(b)若檢測到頻率跳變，先回到步驟1再轉入步驟2，即開始新SPSF內的參數估計。

(2)運算復雜度分析：以復數乘次數來考察運算復雜度，忽略峰值提取(可通過數值比較實現)、反正弦、反正切函數以及標量冪運算計算量，矩陣求逆采用原始定義。

6 仿真與分析

實驗1 對異步網臺信號實時估計的正確性

圖2(a)是頻率的實時跟蹤結果，可見：算法分別在第19, 31, 49, 61個樣點處檢測到跳頻發生，與真實跳頻情況一致；算法能夠實時準確估計多個異步FH信號頻率，且頻率估計值能迅速收斂至真實值，驗證了新粒子生成方法的有效性。圖2(b)和圖2(c)是2D-DOA的實時估計偏差，可以看出，算法能夠實現對2D-DOA的實時精確估計，在各FRT穩定期，估計誤差小于。相比于頻率偏差，2D-DOA偏差的震蕩幅度略大，這主要是由誤差累積導致的，但估計誤差已能滿足絕大多數場合應用需要。

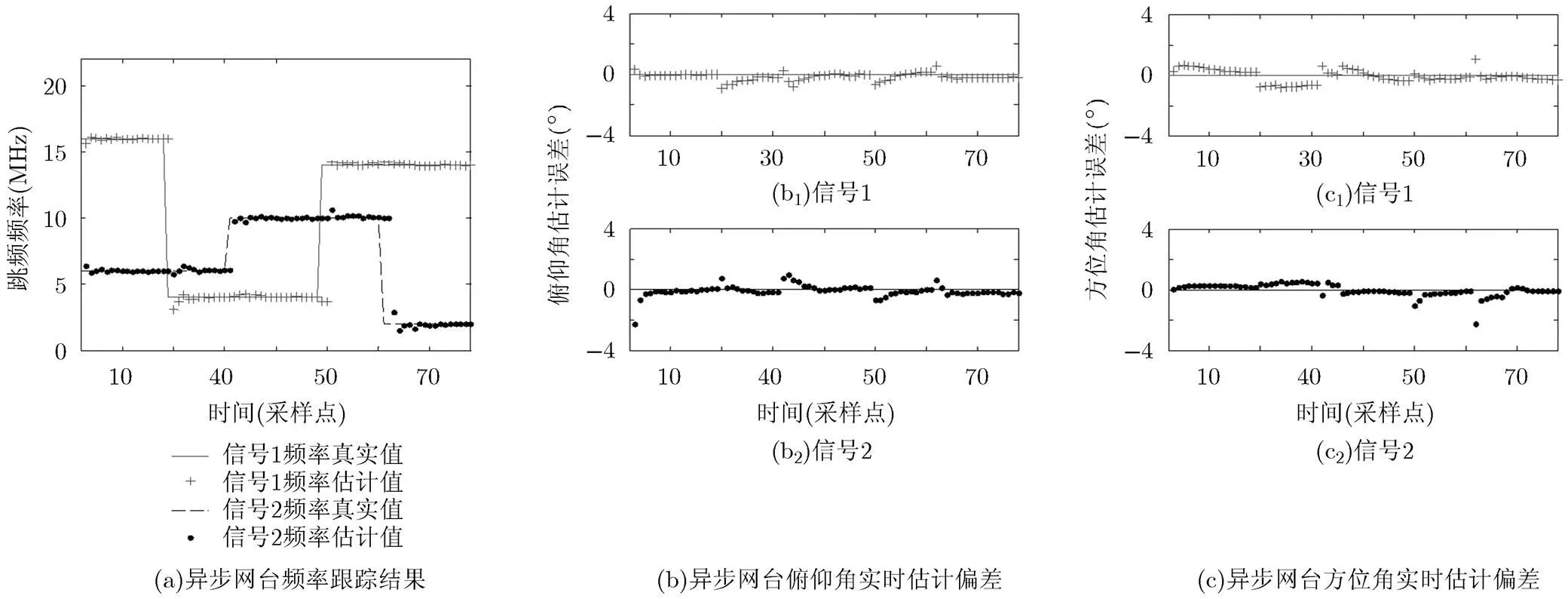
圖2 異步網臺頻率跟蹤與2D-DOA實時估計結果

實驗2 對同步網臺信號實時估計的正確性

觀測窗包含完整的3跳信號，兩信號同時在第31, 61采樣點處發生跳頻，其余條件與實驗1相同。

頻率跟蹤結果如圖3(a)所示。可見，算法分別于第31和61樣點處檢測到跳頻發生，與真實跳頻情況一致；算法能夠實時準確估計多個同步FH信號頻率，且頻率估計值能迅速收斂至真實值。對比圖3(a)和圖2(a)發現，總體上看，同步組網時，頻率估計精度更高，這主要由于在同等條件下(采樣率、跳周期均相同)，同步組網時各FRT相對更長(異步組網時，兩信號到達時刻隨機，駐留時間長度隨機)，更利于算法收斂。圖3(b)和圖3(c)是2D-DOA的實時估計偏差，可見，本文方法能夠對同步FH信號的2D-DOA進行實時精確估計；在各FRT的穩定期，估計誤差小于

圖3 同步網臺頻率跟蹤與2D-DOA實時估計結果

實驗3 驗證算法對跳時刻的檢測性能

采用正確檢測概率評價跳時刻檢測性能。兩信號跳頻集與實驗1、實驗2相同，觀測樣點數設為32，信號1在第17個采樣點發生跳頻，信號2在觀測時間內頻率保持不變。每次試驗，兩信號的跳頻頻率均在跳頻集中隨機選擇。正確檢測的定義為：檢測到跳頻發生次數為1，且位置為第17或第18采樣點。不同信噪比下進行100次獨立實驗，本文方法與文獻[11]的正確檢測概率如圖4所示。

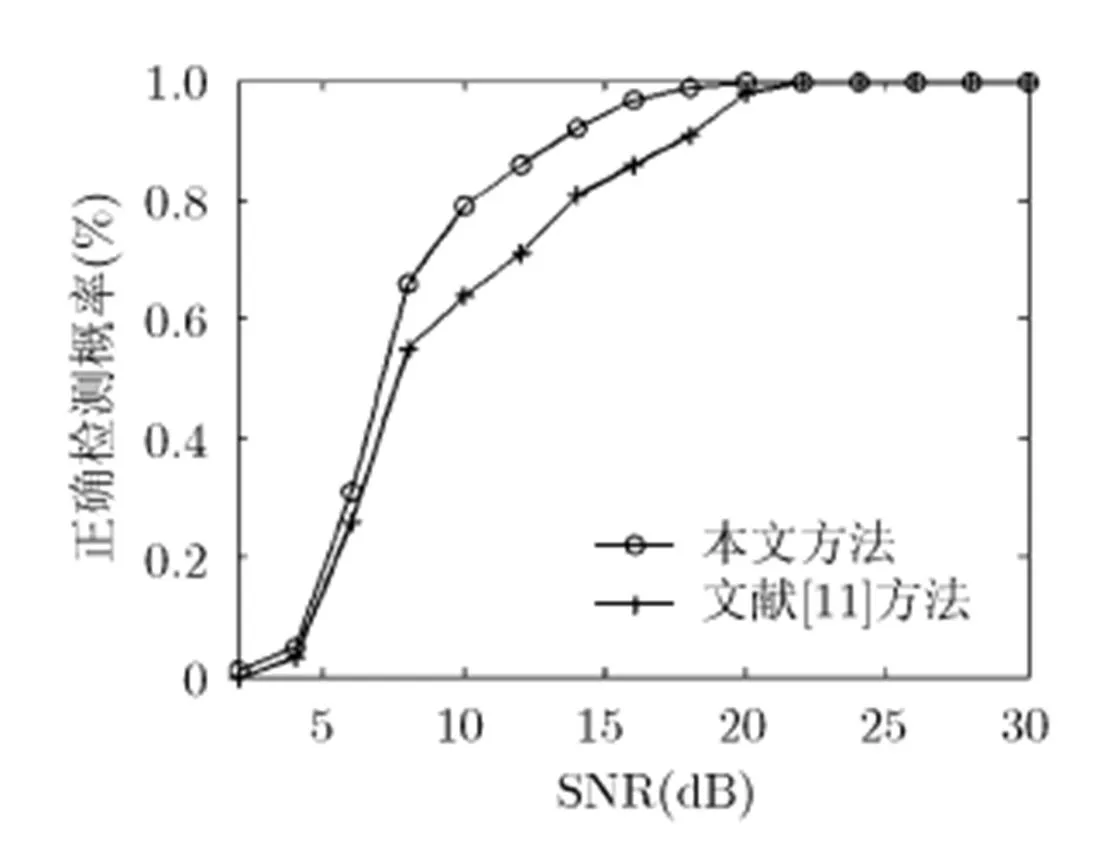
圖4 跳時刻正確檢測概率

由圖可見，本文方法的跳時刻檢測性能優于文獻[11]，主要原因在于：一是采取新的粒子生成方法使初始粒子分布于真實空間相移因子周圍的概率顯著增大，易于快速收斂，導致頻率估計值和求解的ARMA模型系數更準確；二是L型陣列相比于ULA可獲得信源更多的有用信息。

實驗4 頻率和2D-DOA的估計性能

仿真條件同實驗3，發生跳頻(第1，第2，第17，第18)的采樣點不參與統計，各參數偏差的定義如式(39)~式(41)：

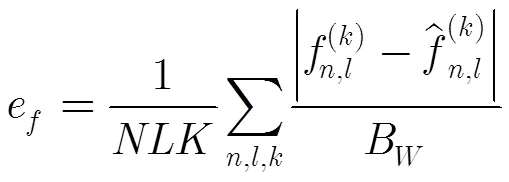
(40)

(41)

圖5 頻率估計性能 ??????????????圖6 俯仰角、方位角估計性能

圖5表明，本文方法對頻率的估計性能優良(信噪比10 dB以上時，估計偏差小于跳頻帶寬的1%)，且優于文獻[11]，原因在于L型陣列可供利用的有效信息更多，且對兩ULA的頻率估計值進行了平均。圖6表明，算法對2D-DOA的估計精度隨著信噪比的提高逐漸變好：信噪比10 dB以上時，方位角和俯仰角的估計偏差均小于。

7 結束語

在電子對抗實時情報支援等對偵察實時性要求很高的場合，需快速估計空間多個跳頻信號的技術參數，本文基于L型陣列提出一種對同步和異步網臺均適用的多跳頻信號頻率跟蹤和2維波達方向實時估計算法。該方法頻率跟蹤速度快，2D-DOA估計準確，且無需參數配對。理論分析和仿真實驗表明，所提方法可以很好地解決FH信號多參數的實時估計問題。如何使所提方法適用于信號源數目隨機變化以及更低信噪比環境有待進一步研究。

[1] ZHAO Lifan, WANG Lu, BI Guoan,. Robust frequency- hopping spectrum estimation based on sparse Bayesian method[J]., 2015, 14(2): 781-793.

[2] 張東偉, 郭英, 齊子森, 等. 多跳頻信號波達方向與極化狀態聯合估計算法[J]. 電子與信息學報, 2015, 37(7): 1695-1701. doi: 10.11999/JEIT141315.

ZHANG Dongwei, GUO Ying, QI Zisen,. Joint estimation algorithm of direction of arrival and polarization for multiple frequency-hopping signals[J].&2015, 37(7): 1695-1701. doi: 10.11999/JEIT141315.

[3] FU Weihong, HEI Yongqiang, and LI Xiaohui. UBSS and blind parameters estimation algorithms for synchronous orthogonal FH signals [J]., 2014, 25(6): 911-920. doi: 10.1109/JSEE.2014. 00105.

ZHAO Xinming, JIN Yan, and JI Hongbing. Parameter estimation of frequency-hopping signals based on Merid filter instable noise environment[J].&2014, 36(8): 1878-1883. doi: 10.3724/ SP.J.1146.2013.01436.

[5] ANGELOSANTE D, GIANNAKIS G B, and SIDIROPOULOS N D. Sparse parametric models for robust nonstationary signal analysis: Leveraging the power of sparse regression[J]., 2013, 30(6): 64-73.

[6] SHA Zhichao, HUANG Zhitao, ZHOUYiyu,. Frequency-hopping signals sorting based on underdetermined blind source separation[J]., 2013, 14(7): 1456-1464.

[7] FU Kuoching and CHEN Yungfang. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems[J]., 2013, 7(9): 883-892.

[8] VALYAKIS A, TSAKONAS E E, SIDIROPOULOSN D,. Stochastic modelling and particle filtering algorithms for tracking a frequency-hopped signal[J]., 2009, 57(8): 3108-3118.

[9] 李世鵬, 趙正予, 黃碩, 等. 一種基于粒子濾波的跳頻信號頻率跟蹤技術[J]. 華中科技大學學報(自然科學版), 2011, 39(9): 33-37. doi: 10.13245/j.hust.2011.09.009.

LI Shipeng, ZHAO Zhengyu, HUANG Shuo,. Frequency tracking technology for frequency-hopping signals using particle filters[J].(), 2011, 39(9): 33-37. doi: 10.13245/j.hust.2011.09.009.

[10] LIU Zhangmeng, HUANG Zhitao, and ZHOU Yiyu. Hopping instants detection and frequency tracking of FH signals with single or multiple channels[J]., 2012, 6(1): 84-89.

[11] SHA Zhichao, LIU Zhangmeng, HUANG Zhitao,. Online hop timing detection and frequency estimation of multiple FH signals[J]., 2013, 35(5): 748-756.

[12] 王豐華, 沙志超, 劉章孟, 等. 基于貝葉斯稀疏學習的多跳頻信號頻率跟蹤方法[J]. 電子與信息學報, 2013, 35(6): 1395-1399. doi: 10.3724/SP.J.1146.2012.01493.

WANG Fenghua, SHA Zhichao, LIU Zhangmeng,.A frequency tracking method for multiple frequency-hopping signals based on sparse bayesian learning[J].&, 2013, 35(6): 1395-1399. doi: 10.3724 /SP.J.1146.2012.01493.

[13] LAROCQUE J R, REILLY J P, and NG W. Particle filters for tracking an unknown number of sources[J]., 2002, 50(12): 2926-2937.

[14] ANDRIEU C and DOUCET A. Joint Bayesian model selection and estimation of noisy sinusoids via reversible jump MCMC[J]., 1999, 47(10): 2667-2676.

[15] 毛維平, 李國林, 謝鑫. 單快拍數據預處理的相干信號波達方向估計[J]. 上海交通大學學報, 2014, 48(10): 1362-1367.

MAO Weiping, LI Guolin, and XIE Xin.DOA estimation of coherent signals with preprocessed single snapshot[J]., 2014, 48(10): 1362-1367.

Online Estimation Algorithm of 2D-DOA and Frequency Tracking for Multiple Frequency-hopping Signals

ZHANG Dongwei①②GUO Ying②ZHANG Kunfeng②QI Zisen②HAN Lifeng①SHANG Yaobo①

①(Research Center of Equipment Development and Application, Air Force Engineering University, Xi’an 710051, China)②(Institute of Information and Navigation, Air Force Engineering University, Xi’an 710077, China)

In order to extract Frequency-Hopping (FH) communication parameters and provide the necessary information for the communication countermeasure, an online estimation algorithm of 2D-DOA and frequency tracking for multiple FH signals is proposed in this paper. Firstly, the data model of the L-array for FH signals is built and the applicability of Auto Regresive Moving Average (ARMA) model to L-array data is proved. Then, the particle filtering is introduced to conduct the online estimation of manifold matrix and the frequency, and the ARMA model is built based on the frequency estimates, depending on which, the online detection of hop timing is obtained. After that , the precise estimation of 2D-DOA can be gained via manifold matrix estimates and without parameter matching. With the rational method of particle generation and the weight updating, the new method makes the estimates of manifold matrix and the frequency reach to the stable value promptly. Finally the the Monte-Carlo simulation results show the effectiveness of the proposed algorithm.

Signal processing; Frequency-Hopping (FH); Frequency estimation; Direction Of Arrival (DOA); Particle filtering; Auto Regresive Moving Average (ARMA) model

TN911.7

A

1009-5896(2016)09-2377-08

10.11999/JEIT151170

2015-10-23；

2016-07-01；

2016-08-09

國家自然科學基金(61401499)，陜西省電子信息系統綜合集成重點實驗室基金(201501A)，航空科學基金(20112096016)

The National Natural Science Foundation of China (61401499), The Foundation of Electronic Information System Integration Laboratory in Shaanxi Province (201501A), The Aviation Science Foundation of China (20112096016)

張東偉zdw_dsp616@163.com

張東偉： 男，1987年生，博士，講師，研究方向為通信信號處理及陣列信號處理.

郭 英： 女，1961年生，博士，教授，博士生導師，研究方向為通信信號處理、自適應信號處理等.

張坤峰： 男，1989年生，博士生，研究方向為通信信號處理及陣列信號處理.