一類擴散型捕食—食餌模型非常值正穩態解的不存在性
周文書,王書臣,王 倩
(大連民族大學 理學院,遼寧 大連116605)
?
一類擴散型捕食—食餌模型非常值正穩態解的不存在性
周文書,王書臣,王倩
(大連民族大學 理學院,遼寧 大連116605)
研究了一類擴散型捕食-食餌模型非常值正穩態解的不存在性問題。 該模型能夠用來描述處于異構環境中的兩個種群的生存狀態。利用極值原理和迭代技巧,給出了該模型不存在非常值正穩態解的一個充分條件。這個結果是對該模型理論研究的一個補充。
捕食-食餌模型;穩態解;迭代技巧
1 問題背景與主要結果
Courchamp和 Sugihara[1]構建了如下異構環境中的一類捕食-食餌模型:

式中,B為食餌密度,C為捕食者密度,K為異構環境的搬運容量,rb和rc分別為食餌和捕食者的增長率,μ為捕食者的捕食率。該模型能夠用來描述在異構環境中的兩個種群的生存狀態。
當考慮到種群在空間Ω中的擴散影響時,上述ODE模型轉化為如下反應-擴散模型:
(1)
式中, Ω?RN為有界光滑區域,ν為?Ω上單位外法向量, db和dc分別表示兩個物種的擴散率,亦稱擴散系數。目前,已有很多關于擴散型捕食-食餌模型的理論研究結果,見參考文獻[2-9]。
模型(1)的穩態解滿足如下奇異橢圓方程組:
為方便討論,不妨設擴散系數都等于1,則上述方程組轉化為
(2)
Du[9]等人研究了一個與模型(1)類似的模型:

模型(1)和(3)的本質區別是后者的解不會發生爆破現象,這說明了模型(1)的復雜性。
Gaucel和Langlais[7]研究了模型(1)解的存在性、大時間行為以及解的爆破現象等。 然而,至今未見有關橢圓方程問題(2)的研究結果。本文的主要目的是研究問題(2)非常值正解的不存在性。主要結果如下:
定理1設rc>rb>1,rc>2,則問題(2)沒有非常值正解。
2 主要結果的證明
為證明定理1,不加證明地引用如下引理:



定理1的證明
假設(B,C)是如下問題的一個正解:
(4)

(5)

-ΔU=rb(1-U)U-φU=U(rb-rbU-φ),
-φΔU-UΔφ-2▽U▽φ=rc(1-φ)φU
即
=rc(1-φ)φ-[rb(1-U)φ-φ2]
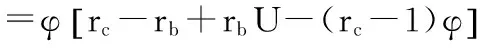
令u=rbU,則(φ,u)滿足
-Δu=u(rb-u-φ),
(6)

(7)
由式(6)得
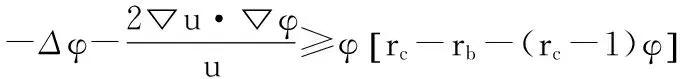
注意到, rc>rb>1,rc>2,則由引理1得

(8)
將式(8)代入式(6)得

由引理1得

(9)
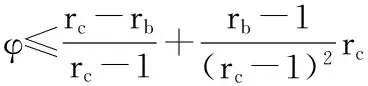
(10)
將式(10)代入式(6)得

由引理1得

(11)
將式(11)代入式(7)得

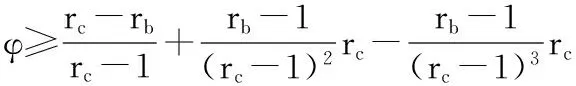
(12)
將式(12)代入式(6)得
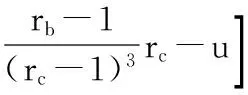
由引理1得

(13)
將式(13)代入式(7)得

由引理1得

通過歸納,知對任意自然數n成立如下關系:
以及

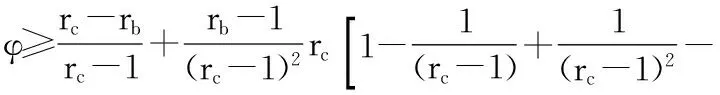


令n→+∞,得
以及

故φ=1,即 V=U。代入V的方程知
-ΔU=0,
這表明U是常數,于是
rb(1-U)=1,
即
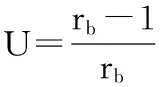
從而

所以,模型(1)只有正常值解。
證畢。
[1] COURCHAMP F, SUGIHARA G. Modelling the biological control of an alien predator to protect island species from extinction[J]. Ecological Applications, 1999,9: 112-123.
[2] MURRAY J D. Mathematical Biology[M]. 3rd ed. Berlin:Biomathematics Series, Springer Verlag, 2002.
[3] WANG M X. Spreading and vanishing in the diffusive prey-predator model with a free boundary[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 23(1): 311-327.
[4] WANG M X, ZhAO Y G. A semilinear parabolic system with a free boundary[J]. Zeitschrift für angewandte Mathematik und Physik, 2015, 66(6): 3309-3332.
[5] GAUCEL S, PONTIER D. How predator food preference can change the destiny of native preys in predator-prey systems[J]. Biological Invasion, 2005, 7: 795-806.
[6] CHEN W, WANG M.Qualitative analysis of predator-prey models with Beddington-DeAngelis functional response and diffusion[J].Math Computer Modelling, 2005, 42: 31-44.
[7] GAUCEL S, LANGLASI M PONTIER D. Invading introduced species in insular hetero -geneous environments[J]. Ecological Modelling, 2005, 18: 62-75.
[8] GAUCEL S. Some remarks on a singular reaction-diffusion system aring in predator-prey modeling[J]. Discrete and Continuous Dynamical System, Series B, 2007, 8(1): 61-72.
[9] DU Y H, HSU S B, A diffusive predator-prey model in heterogeneous Environment [J].J Differential Equations, 2004, 203: 331-364.
[10]LOU Y, NI W M. Diffusion, self-diffusion and cross-diffusion[J]. Journal of Differential Equations, 1996, 131: 79-131.
(責任編輯鄒永紅)
Nonexistence of Non-constant Positive Stationary Solution for a Diffusive Prey-predator Model
ZHOU Wen-shu, WANG Shu-chen, WANG Qian
(School of Science, Dalian Minzu University, Dalian Liaoning 116605, China)
The nonexistence of positive stationary solution for a prey-predator model with diffusion is studied. The model can be used to describe the survival state of two species in heterogeneous environments. By means of the maximum principle and iterative technique, a sufficient condition for the nonexistence is given. This result complements some previous results on the model.
prey-predator model; stationary solutions; iterative technique
2096-1383(2016)05-0492-04
2016-05-25
國家自然科學基金項目(11571062); 遼寧省高等學校杰出青年學者成長計劃(LJQ2013124); 中央高校基本科研業務費專項資金資助項目(DC201502050202)。
周文書(1974-),男,黑龍江齊齊哈爾人,教授,博士,博士生導師,主要從事非線性偏微分方程研究。
O175.2
A

