參數方程應用探析

◇　山東　劉淑霞

(作者單位：山東省棲霞市第一中學)

?

參數方程應用探析

◇山東劉淑霞

參數方程是曲線的另一種表現形式,它彌補了普通方程表示曲線的不足,使得對曲線的研究更加靈活,進一步拓寬了解決問題的思路.下面就對此進行系統梳理,希望幫助同學們查漏補缺、溫故知新.

1　常用曲線的參數方程

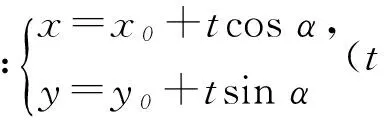
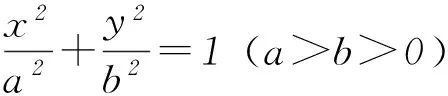
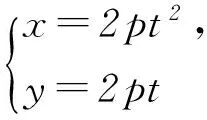
注意:參數方程轉化為直角坐標方程時,消去參數方程中的參數即可,但要注意直角坐標方程中變量x、y的取值范圍應與參數方程中參數的取值對應,消去參數的具體方法要根據參數方程的特點來考慮.

直角坐標方程化為參數方程,要恰當地選擇參數t和函數x=f(t),并且使x=f(t)的值域與直角坐標方程中變量x的范圍一致,然后將x=f(t)代人直角坐標方程中解出y=g(t),即得參數方程.

2　曲線參數方程的應用

2.1利用參數方程求距離

直線的參數方程中參數t的幾何意義與距離有關,適宜求弦長或距離.

2.2利用參數方程求軌跡

求2條動曲線交點的軌跡方程,常選出一個適當的參數,求出2條動曲線方程或動點坐標適合的含參數等式,再消參,即得所求動點軌跡方程.

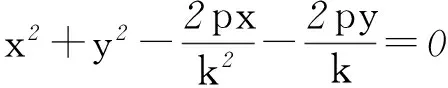
①

x2+y2-2pk2x+2pky=0.

②

因為P(x,y)是異于O點的2圓交點,所以x≠0,y≠0,由式①-②并化簡得

y=(k-1/k)x.

③

由式①+②并化簡得

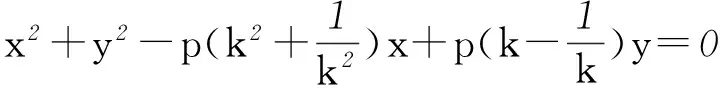
④

由式③得k-1/k=y/x.

⑤

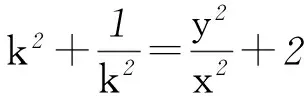
⑥

將式⑤、⑥代入④得x2+y2-2px=0 (x≠0).故點P的軌跡為以(p,0)為圓心,p為半徑的圓(除去原點).

2.3利用參數方程研究最值

圓與橢圓的參數方程能夠很輕松地利用角表示出圓與橢圓上的點,因此凡是與圓、橢圓上的動點有關的最值問題都可用參數方程解決.

(1) 寫出曲線C的參數方程、直線l的普通方程;

(2) 過曲線C上任一點P作與l夾角為30°的直線,交l于點A,求|PA|的最大值與最小值.

其中α為銳角,且tanα=4/3.

總之,涉及到直線、圓、橢圓、雙曲線的部分試題,若用其參數方程來解決,在化歸、轉換等環節會帶來極大的方便,使得運算過程流暢,從而提高解題速度.

(作者單位：山東省棲霞市第一中學)