GRNN在學生寫作成績預測中的應用研究
胡帥,顧艷,姜華(渤海大學 大學外語教研部,遼寧 錦州 121013)
GRNN在學生寫作成績預測中的應用研究
胡帥,顧艷,姜華
(渤海大學 大學外語教研部,遼寧 錦州121013)
由于學生英語寫作成績預測受諸多因素影響,具有高維、非線性特點,本文基于廣義回歸神經(jīng)網(wǎng)絡(GRNN)算法原理,構建了GRNN學生英語寫作成績預測模型,并與彈性BP算法改進的BP神經(jīng)網(wǎng)絡模型的預測結果進行對比分析。仿真結果表明:改進的BP神經(jīng)網(wǎng)絡模型的預測最大相對誤差為3.23%,GRNN模型的預測最大相對誤差僅為-0.72%,表明所建立的GRNN模型的預測精度高、泛化能力強、收斂速度快、調整參數(shù)少,驗證了將GRNN應用于英語寫作成績預測方案的可行性。
廣義回歸神經(jīng)網(wǎng)絡;BP神經(jīng)網(wǎng)絡;成績預測;模型
對學生英語寫作成績的準確預測可為教師調整寫作教學方法和學生自主學習提供有益參考。傳統(tǒng)的預測方法采用簡單的線性模型來預測。由于影響學生英語寫作成績的因素很多,使學生英語寫作成績預測呈現(xiàn)高維、非線性特性,所以,傳統(tǒng)方法的預測結果誤差較大,難以滿足實際需要。隨著人工神經(jīng)網(wǎng)絡技術的快速發(fā)展,基于神經(jīng)網(wǎng)絡的數(shù)據(jù)挖掘方法為學生英語寫作成績預測提供了新的解決途徑。廣義回歸神經(jīng)網(wǎng)絡(General Regression Neural Network,GRNN)算法簡單、逼近精度高、具有良好的非線性收斂性能[1]。文中嘗試構建基于GRNN[2-4]的大學生英語寫作成績預測模型,以期解決傳統(tǒng)方法預測精度不高的問題,并與彈性BP算法改進的BP網(wǎng)絡模型作對比,驗證GRNN預測模型的有效性。
1 GRNN的算法理論基礎
GRNN由輸入層、模式層、求和層、輸出層4部分構成[5]。令隨機向量X和隨機變量Y的概率密度函數(shù)為f(X,Y),當X= X0時,則Y對X0的回歸值的計算方法如式(1)所示,樣本集(Xi,Yi),(i=1,2,3,…,n)非參數(shù)估計如式(2)所示。

式(2)中n為訓練樣本容量,w為樣本向量維數(shù),SPREAD為徑向基函數(shù)的分布密度,d表示樣本向量之間的歐式距離,計算方法如式(3)和式(4)所示。將式(3)和式(4)代入式(2)并經(jīng)過化簡最終可得式(5),由式(5)可知,徑向基函數(shù)的分布密度SPREAD是唯一人為可調參數(shù)[6-7],只要取值適中,即可將所有訓練樣本的因變量綜合進行考慮,且此時不同訓練樣本點與測試樣本點之間的距離也一并進行計算,離測試樣本點接近的訓練樣本點將會獲得更大的權值[8]。


2 GRNN預測模型的建立
2.1寫作成績評價的指標體系構建
以往研究表明學生英語寫作成績受多種因素影響,如漢語寫作能力、口語能力、詞匯水平、,語法、文化因素等。本文基于已有研究發(fā)現(xiàn)并進一步細化,最終確定用于學生寫作成績預測的評價指標體系共包括12項評價指標。分別為:口語(X1)、聽力(X2)、詞匯(X3)、語法(X4)、閱讀(X5)、翻譯(X6)、學習動機(X7)、學習興趣(X8)、跨文化交際能力(X9)、寫作策略(X10)、語篇知識(X11)和英美文化知識(X12)。
2.2原始數(shù)據(jù)獲取
學生英語寫作評價體系中的X2、X5和X6三項得分依據(jù)學生大二第一學期英語四級考試分項成績(均折合成滿分為10分);X1由口語測試獲得;X3、X4、X11和 X12分別由測試獲得;X7、X8、X9和X10分別由問卷調查獲得。為了提高預測模型的準確性、和保證樣本數(shù)據(jù)的科學性,將采集到數(shù)據(jù)中的傾向性數(shù)據(jù)(評分全部為滿分或全部為零分的數(shù)據(jù))剔除,保留有效數(shù)據(jù)后,計算60位學生的各指標的平均得分,獲得用于學生寫作成績預測的原始數(shù)據(jù)如表1所示。

表1 預測原始數(shù)據(jù)
2.3分布密度參數(shù)的確定
在建立GRNN時,分布密度SPREAD的取值直接影響GRNN的逼近性能,SPREAD的值越小,GRNN的逼近精度越高,但取值過小將會產(chǎn)生過擬合現(xiàn)象;SPREAD的值越大,GRNN的逼近精度越低,但擬合曲線相對較為平滑[8]。文中采用循環(huán)訓練算法,在SPREAD=0.3,0.4,0.5,0.7,1.0情況下,利用GRNN對1-40號訓練樣本進行逼近實驗,不同SPREAD值條件下的GRNN逼近結果對比如圖1所示。從圖1可以看出,當SPREAD=0.3時,GRNN相對誤差最小,幾乎為0,此時逼近性能最佳,所以,文中在建立GRNN預測模型時,最終確定SPREAD的值為0.3。
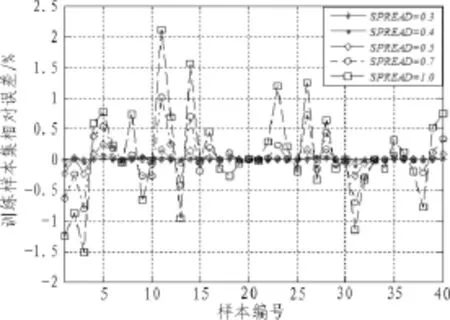
圖1 不同SPREAD值條件下的GRNN逼近結果對比
2.4BPNN模型參數(shù)的確定
本文采用GRNN模型對寫作成績進行預測,并用彈性BP算法改進的BPNN模型作為對比預測模型。對于標準BPNN模型,經(jīng)反復試驗,最終確定其網(wǎng)絡拓補結構為12-15-1;隱含層傳遞函數(shù)采用tansig函數(shù);輸出層傳遞函數(shù)采用purelin函數(shù),采用基于彈性BP算法的訓練函數(shù)trainrp;學習函數(shù)采用learngdm;誤差性能函數(shù)采用均方誤差函數(shù)mse;學習速率設為0.1。
3 仿真實驗
3.1預測模型的訓練
目標精度設為0.001、最大迭代次數(shù)設為10 000,將表1 中1-40號樣本作為訓練樣本集,分別對GRNN與BPNN預測模型進行訓練。GRNN與BPNN對于訓練樣本集的相對誤差曲線如圖2所示。可以看出,所建立的2種預測模型均具有較高的逼近能力,GRNN預測的相對誤差幾乎為0,與實際值幾乎完全一致;BPNN預測的最大相對誤差達到-1.71%,并且在訓練樣本區(qū)間內相對誤差波動較大。這表明,與BPNN預測模型相比,GRNN預測模型在逼近能力、學習速度上都具有明顯優(yōu)勢。
3.2預測模型的泛化能力測試
將表1中41-60號樣本作為測試樣本集,對GRNN與BPNN預測模型進行泛化能力測試。GRNN與BPNN的預測結果如圖3所示。GRNN與BPNN對于測試樣本集的相對誤差曲線如圖4所示。從圖3和圖4可以看出,GRNN與BPNN都達到了較高的預測精度,GRNN對測試樣本集預測的最大相對誤差僅為-0.72%,但是,BPNN預測的最大相對誤差已經(jīng)達到3.23%,并且在測試樣本區(qū)間內誤差波動范圍較大。這說明GRNN在逼近能力和學習速度上較BPNN有更大優(yōu)勢,仿真實驗發(fā)現(xiàn),所建立的GRNN模型即使樣本數(shù)據(jù)較少,但是預測效果依然很好,而BPNN模型則需大量樣本才能進一步提高其預測精度,但這勢必增大網(wǎng)絡模型的復雜程度,并且如何確定BPNN的拓補結構、如何選取傳遞函數(shù)、如何避免局部極小值以及網(wǎng)絡收斂速度過慢都使其在應用時存在很大局限性。
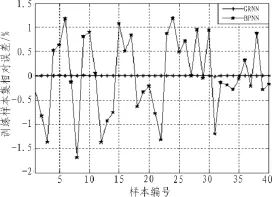
圖2 GRNN與BPNN對于訓練樣本集的相對誤差

圖3 GRNN與BPNN的預測結果

圖4 GRNN與BPNN對于測試樣本集的相對誤差
4 結 論
本文應用GRNN對在校大學生英語寫作成績進行預測分析,仿真結果表明,盡管學生英語寫作成績的影響因素很多,呈現(xiàn)較大的非線性,但是,因為GRNN的人為調節(jié)參數(shù)很少,具有很強的非線性映射能力,故所建立的GRNN預測模型的運行速度、預測準確性都明顯優(yōu)于BP網(wǎng)絡,可以較好地完成寫作成績預測任務,具有較強的實際操作性。
[1]丁碩,常曉恒,巫慶輝,等.基于GRNN與BPNN的二維向量模式分類對比研究[J].國外電子測量技術,2014,33(5):56-58.
[2]王曉光,周慧,張有君.應用GRNN模型對給水管網(wǎng)水質的綜合評價[J].沈陽理工大學學報,2011,30(4):63-66.
[3]DING Shuo,CHANG Xiao-heng,WU Qing-hui.A Study on Approximation Performances of General Regression Neural Network[J].Applied Mechanics and Materials,2014(441): 713-716.
[4]DING Shuo,CHANG Xiao-heng,WU Qing-hui.Application of General Regression Neural Network in Characteristic Curve Fitting of Optical Fiber Micro-bend Sensor[J].Applied Mechanics and Materials,2014(441):116-119.
[5]丁碩,常曉恒,巫慶輝.GRNN與BPNN的函數(shù)逼近性能對比研究[J].現(xiàn)代電子技術,2014,37(7):114-117.
[6]賈花萍.GRNN神經(jīng)網(wǎng)絡在電力系統(tǒng)負荷預報中的應用[J].電子設計工程,2012,20(3):14-16.
[7]郭婉娥.Elman與GRNN神經(jīng)網(wǎng)絡模型在水環(huán)境承載力評價中的應用——以文山州區(qū)域水環(huán)境承載力評價為例[J].水資源與水工程學報,2013,24(4):184-188.
[8]何漢林,孟愛華,祝甲明,等.基于優(yōu)化的GRNN和BP神經(jīng)網(wǎng)絡的磁滯曲線擬合對比分析[J].機電工程,2013,30(1): 116-120.
【相關參考文獻鏈接】
楊藝,虎恩典.基于S函數(shù)的BP神經(jīng)網(wǎng)絡PID控制器及Simulink仿真[J].2014,22(4):29-31.
任偉建,陳奕君.基于神經(jīng)網(wǎng)絡的移動機器人多傳感器數(shù)據(jù)融合研究.2014,22(12):5-8.
李鋼,呂國芳.基于正則化RBF神經(jīng)網(wǎng)絡的混凝土強度預測[J]. 2014,22(13):52-54.
閆妍,張云鵬,張一弛,等.基于BP神經(jīng)網(wǎng)絡的食品價格的預測[J].2014,22(15):47-49.
劉朝云,翟春燕,李書臣,等.神經(jīng)網(wǎng)絡專家系統(tǒng)在電機故障診斷中的應用[J].2014,22(15):159-161.
費晶,李趙興.基于BP和RBF神經(jīng)網(wǎng)絡的新型融合技術研究[J]. 2014,22(17):96-98.
管艷娜,李孝安.基于神經(jīng)網(wǎng)絡專家系統(tǒng)的推理研究[J].2014,22(20):20-22.
鄒云.基于神經(jīng)網(wǎng)絡的海面溢油圖像分類算法[J].2014,22 (20):168-170.
樊潤潔,朱亞男.基于神經(jīng)網(wǎng)絡的傳感器非線性誤差校正方法[J].2014,22(23):56-59.
Study of application of GRNN in student writing score prediction
HU Shuai,GU Yan,JIANG Hua
(Teaching and Research Institute of Foreign Languages,Bohai University,Jinzhou 121013,China)
Prediction of student English writing scores is influenced by various factors.It has high dimensional and nonlinear features.A prediction model of students’English writing scores was established in this paper.The model was based on the algorithm principle of generalized regression neural networks(GRNN).Its prediction result was analyzed and compared with that of a BP neural network model improved by resilient back-propagation.The simulation results indicate that:the largest relative error of prediction produced by improved BP neural network model is 3.23%,while the one produced by GRNN model isonly-0.72%.This implies that the GRNN model has higher prediction accuracy,better generalization ability,faster convergence speed and less adjusting parameters.Thus the feasibility of applying GRNN to English writing score prediction is verified.
general regression neural network;BP neural network;score prediction model
TN609
A
1674-6236(2016)11-0015-03
2015-07-14稿件編號:201507105
遼寧省教育廳科學研究一般項目(W2015015);遼寧省社會科學基金資助項目(L14CYY022)
胡 帥(1980—),女,黑龍江雙鴨山人,碩士,講師。研究方向:語料庫語言學、神經(jīng)網(wǎng)絡理論及其應用研究。

