具有變系數的高階中立型時滯差分方程的振動性
黃梅
(湖南第一師范學院 數學與計算科學學院,湖南 長沙 410205)
具有變系數的高階中立型時滯差分方程的振動性
黃梅
(湖南第一師范學院 數學與計算科學學院,湖南 長沙 410205)
研究一類具連續變量的高階中立型差分方程的解的振動性,給出了有界解振動的充分條件。
差分方程;有界解;振動;非振動
1.引言
由于醫學、生物數學、現代物理等自然科學和邊緣學科的迅速發展,提出了許多由差分方程描述的具體數學模型.關于離散變量的差分方程的振動性研究已有很長歷史.近些年來,對具有連續變量的差分方程振動性的研究也有了一些結果,如文[1-6],對具有連續變量的中立型差分方程解的振動性研究,可見文[7-9],另外,關于具有連續變量的二階或偶數階中立型差分方程解的振動性研究,有文[10-12].
本文研究具有連續變量的變系數高階中立型時滯差分方程
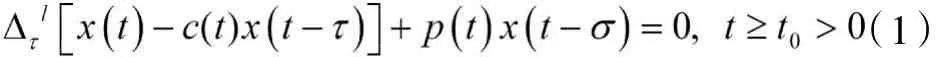
2.定理與證明
為了研究方程(1)解的振動性,要用到文[13]中的引理:
引理設存在常數α(0≤α<1),使得α≤ c(t)<1.若是(1)的最終有界正解,令,則最終成立
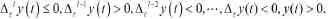
定理設(H)成立.若存在常數α,使得α≤c (t)<0,且對k>1,有

以及對t≥t0,有則方程(1)的所有有界解振動.

對此η,由(2)可知,必存在t2≥t1,使得

由(1),得
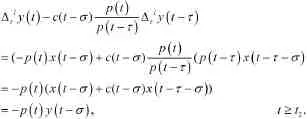
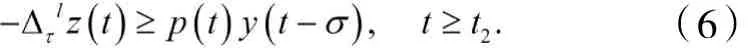
而且易證得
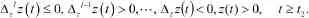
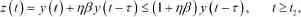
因而
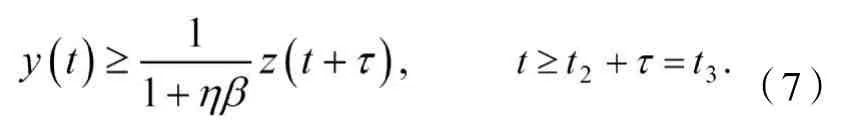
將(7)代入(6),得
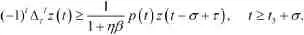
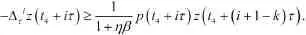
對上式從i到n(n≥i)求和,得
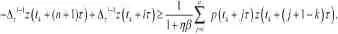
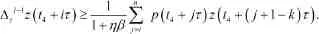
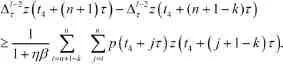
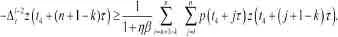
將上述過程重復 -1次,得
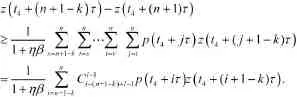
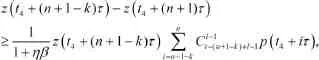
所以
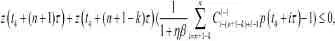
這與(4)矛盾,定理得證.
[1]申建華.具有連續變量差分方程振動性的比較定理及應用[J].科學通報,1996,41(16):1441-1444.
[2]LADAS G,PAKULA L,WANG Z.Necessary and sufficient conditions for the oscillation of difference equations[J].1992,2(1):17-26.
[3]周展,黃立宏.具有連續變量的非線性差分方程的振動性[A].劉永清主編.微分方程理論與應用[C].海口:南海出版公司,1998,203-205.
[4]張玉珠,燕居讓.具有連續變量的差分方程振動性的判據[J].數學學報,1995,38(3):406-411.
[5]周勇.具有連續變量的變系數差分方程的振動性[J].經濟數學,1996,13(1):86-89.
[6]韓振來.具連續變量的非線性時滯差分方程的振動性[J].應用數學與計算數學學報,1999,13(1):60-64.
[7]熊萬民,王志成.具連續變量的中立型差分方程的振動性[J].湖南大學學報,2001,28(1):8-12.
[8]廖新元,朱惠延.具有連續變量的中立型差分方程的振動性[J].數學理論與應用,2002,22(2):27-30.
[9]劉召爽,吳淑慧.連續變量一階中立型差分方程的振動性[J].河北師范大學學報,2002,26(2):113-117.
[10]黃梅,申建華.具連續變量的二階中立型差分方程[J].湖南師范大學自然科學學報,2005,28(3):4-6.
[11]黃梅,申建華.具連續變量的偶數階中立型差分方程的振動性[J].純粹數學與應用數學,2006,22(3):399-404.
[12]黃梅,申建華.具連續變量的偶數階中立型差分方程[J].西南大學學報(自然科學版),2007,29(10):29-34.
[13]黃梅.具有連續變量的變系數偶數階差分方程的有界振動[J].湖南第一師范學院學報,2013,13(3):103-105.
[責任編輯:胡偉]
Oscillation for a Class of High Order Neutral Delay Difference Equations with Variable Coefficients
HUANG Mei
(Department of Mathematics,Hunan First Normal University,Changsha,Hunan 410205)
This paper investigates the oscillation of solution for a class of high order neutral difference equations with continuous a.The sufficient condition for bounded oscillation of the solutions is obtained.
difference equation;bounded solution;oscillation;nonoscillation
O175.7
A
1674-831X(2016)02-0095-02
2015-10-16
黃梅(1965-),女,湖南常德人,湖南第一師范學院教授,主要從事常微分方程研究。

