正浮力開放腔體圓柱殼垂直入水數值研究

路中磊， 魏英杰， 王　聰， 陳　晨

(哈爾濱工業大學 航天學院，哈爾濱　150001)

?

正浮力開放腔體圓柱殼垂直入水數值研究

路中磊， 魏英杰， 王聰， 陳晨

(哈爾濱工業大學 航天學院，哈爾濱150001)

開放腔體結構以開口端撞擊水面引起腔體內部氣體介質流動，并與殼體下沉運動相互耦合，形成獨特的運動特征和流場特性．基于均質平衡流理論，針對具有正浮力特性的開放腔體圓柱殼模型低速垂直入水運動進行了三維數值模擬，得到入水過程中的運動軌跡、軸向壓差阻力波動特性及入水空泡發展規律，結果表明：開放腔體具有較好的緩沖作用；腔體內氣體運動分為沖擊振蕩和壓縮振動先后兩個截然不同的運動過程；氣體振動具有高頻率、低幅值、快衰減特點，對殼體下沉運動具有擾動作用，同時導致開口端以同頻率吸入-排出液體，形成復雜的流場環境，使空泡壁面發生波動，并過早脫落潰滅。

入水；開放腔體圓柱殼；正浮力；數值模擬

航天飛機固體火箭助推器(Solid Rocket Bosters，SRB)[1]在完成運載任務后墜入海洋，入水過程助推器基本保持豎直姿態，其噴管首先撞擊海平面，海水流入燃料貯箱段，使助推器內部形成充滿氣體的封閉腔體，導致其等效密度小于海水，形成一種氣浮結構[2]，從而方便打撈，實現可重復使用目的。火箭助推器可以簡化成下端面開放、上端面封閉，且具有正浮力特性和開放腔體的圓柱型殼體結構，其入水過程涉及腔體內氣體漲縮運動與殼體自身浮沉運動之間的耦合作用，使氣-液兩相介質流動復雜，存在沖擊、下沉、上浮再出水兩次穿越氣液交界面過程，相對于傳統回旋體結構入水過程[3]，特別是入水沖擊、流體動力、入水空泡和彈道等方面均具有較明顯差異。

國內外對回轉體結構入水過程的研究已經取得了一定成果，WORTHINGTON[4]借助高速攝像機對液滴與球體入水過程進行拍攝，首次對入水過程中噴濺、入水空泡等現象進行了描述；1958年美國啟動水星計劃，針對航天器入海回收問題中結構體入水過程進行了大量研究[5-6]；MAY[7-9]測量了球體入水阻力系數，并分析了表面黏度及等效質量對入水過程的影響；MAY[10]研究了火箭助推器零度攻角入水過程中入水空泡的生成、發展及潰滅過程，并分析了入水過程中流場變化過程等問題；GEKLE等[11]分析了圓柱體入水空泡深閉合與FROUDE數之間的關系；YAN等[12]分析了低雷諾數條件下對細長體結構入水空泡的流體動力特性；HE等[13]分析了入水速度對泡內壓力的影響及空泡內部壓力分布；何春濤等[14]對圓柱體串聯和并聯入水過程進行了實驗，并分析了串聯和并聯入水特性。對于殼體結構入水的研究主要集中在沖擊載荷及結構響應等方面，BROOKS等[15]對返回艙撞擊液面過程進行的數值計算和水槽試驗，分析了運動速度和質量對沖擊力的影響；趙蛟龍等[16]分析了圓柱空腔結構入水沖擊過程流體動力載荷及結構響應。目前，在國內外公開發表的文獻中，對正浮力開放腔體結構入水全過程及相關問題的研究尚未見到。

本文對具有正浮力特征的開放腔體圓柱殼結構零攻角低速垂直入水過程開展了三維數值模擬研究，并通過對流體動力與入水彈道進行耦合計算，得到其入水過程中殼體入水運動軌跡、軸向作用力變化規律、殼體壁面壓力分布和發展規律及入水空泡的發展規律，并對腔體內封閉氣體運動及其對入水運動規律和流體動力特征的影響進行了分析。

1　數值計算理論

1.1控制方程

計算采用VOF(Volume of Fluid)多項流模型，其將氣液兩相流視作一種混合流體，氣液兩相摻混但不相融，體積分數滿足歸一化條件：

αl+αg=1

(1)

式中：α為體積分數，下標l表示液體、g表示氣體。

連續性方程：

(2)

式中：ρm=αlρl+αgρg為混合密度，下標m表示氣液混合物；ui為i方向速度。

動量方程：

(3)

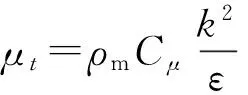
能量方程：

(4)

絕熱條件氣體狀態方程：

(5)

1.2湍流模型

本文選用RNGk-ε兩方程湍流模型，其具有較好的魯棒性，對低雷諾數流動具有較高的精度。具體湍流模型輸運方程如下：

湍動能輸運方程：

Gk+Gb-ρmε-Ym

(6)

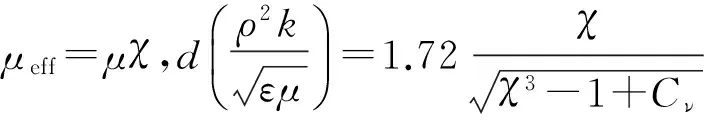
湍動耗散率輸運方程：

(7)

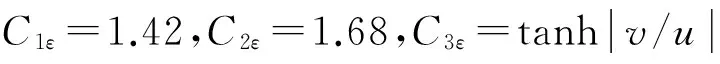
2　數值方法

2.1計算方法及模型

本文對殼體垂直入水過程進行三維單自由度數值模擬，對于低速垂直入水情況，未考慮氣液兩相間相變過程，并忽略橫向擾動影響，僅考慮了豎直方向運動，給定初始運動條件，即初始距水面高度和初始運動速度，通過對流體動力與運動參數耦合求解，得到開放腔體圓柱殼入水過程中的運動規律和受力情況。

基于Fluent軟件平臺，采用有限體積法(Finite Volume Method，FVM)在三維計算流域內對雷諾時均化納維斯托克斯方程(Reynolds Averaged Navier-Stokes，RANS)進行離散化求解。對方程中瞬態項采用時間推進離散格式，對流項采用二階精度的(Quadratic Upstream Interpolation for Convective Kinetics，QUICK)離散格式，擴散項采用二階精度的中心差分離散格式，擴散項中梯度項采用基于單元體的最小二乘法差值(least-quares cell based)的離散格式進行離散化處理。采用PISO(Pressure Implicit with Splitting of Operators)算法對壓力和速度進行耦合迭代，時間步長1×10-5s。

計算模型見圖1，為充分體現具有開放腔體的殼體入水運動和流體動力特征，并考慮對問題簡化，本文選用一端完全開放且具有較大腔體的圓柱殼幾何模型，并以ly12鋁合金和不銹鋼密度為參照，結合正浮力特征(等效密度小于液體密度)設定模型幾何尺寸，進而確保驗證性實驗實施的可能。模型幾何尺寸和力學參數見表1。

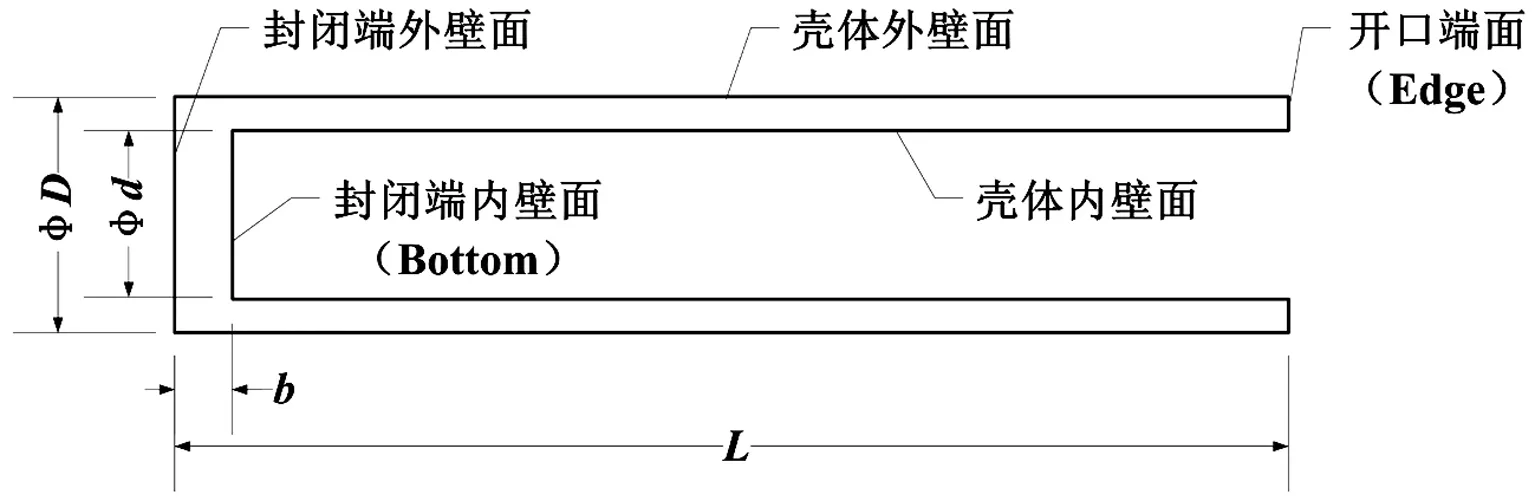
圖1　開放腔體圓柱殼剖面示意圖Fig.1 Sketch of profile of un-closed solid cavity cylinder

長度L/m外徑D/m內徑d/m封閉端厚度b/m質量M/kg等效密度ρ/(kg·m-3)0.350.060.0540.006250.785793.5

2.2計算流域邊界條件及網格劃分

以撞擊自由液面時刻為時間零點，自由液面位置為坐標原點，重力方向為運動正方向。計算流域及邊界條件設定(見圖2)，選用圓柱型計算流域，氣體流域長4L，液體流域長8L，流域直徑長15D，參考壓力p∞=101 325 Pa，重力加速度g=9.8 m/s2，氣液間表面張力系數0.072。選取空氣流域頂部為壓力入口邊界，相對壓力0 Pa，入口空氣溫度293 K；液體流域底部為壓力出口邊界，相對壓力27 390 Pa，出口液體溫度283 K；流域側壁為滑移壁面邊界。

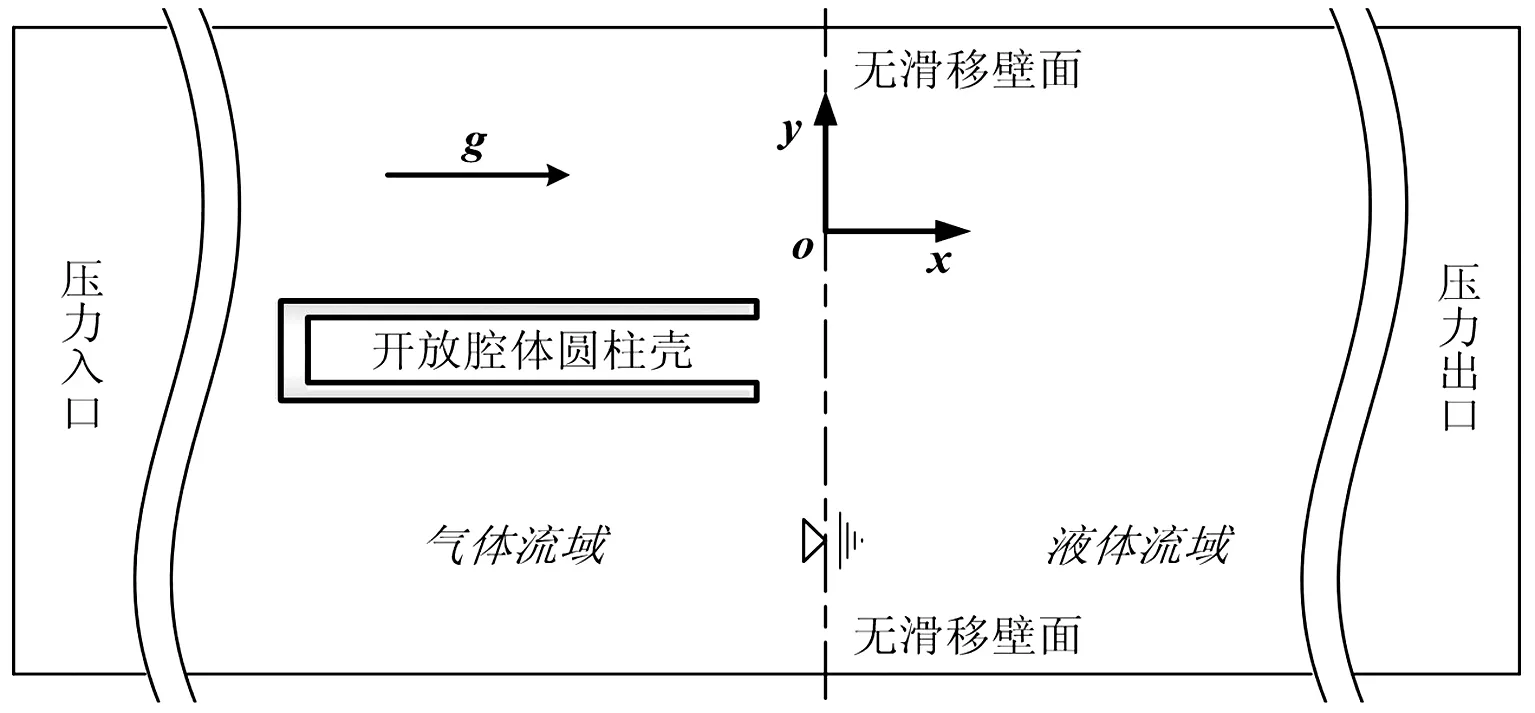
圖2　計算流域及邊界條件Fig.2 Schematic of computation domain and boundary conditions

計算網格見圖3，對開放腔體圓柱殼模型及流域均采用結構網格劃分，為更好的捕捉運動過程中流體動力特征，在殼體附近及流體參數可能出現畸變的位置進行了網格加密處理。

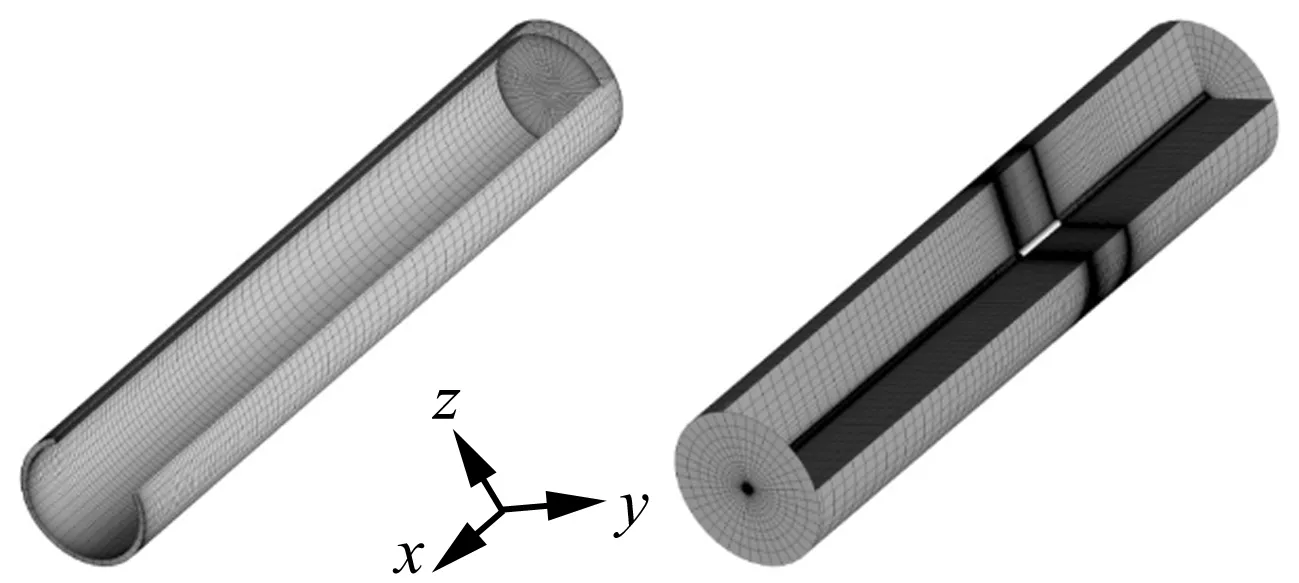
圖3　計算網格Fig.3 Grid scheme

3　結果分析

正浮力開放腔體圓柱殼結構入水過程具有運動過程復雜、流場參數變化劇烈等特點，現依據1 m/s速度入水條件下的計算結果，分別對開放腔體圓柱殼入水運動規律、軸向作用力變化規律、表面壓力分布和入水空泡發展規律進行分析。

3.1入水運動規律分析

殼體開口端面的運動規律和軸向速度變化規律(見圖4)，對比相同初始條件的實驗結果，運動軌跡除了沉至最深和浮至最高處外，數值結果與實驗結果具有較好的一致性。正浮力殼體入水運動具有先后兩個明顯不同的運動階段，分別為入水下沉階段和起伏振蕩階段，下面針對這兩個階段運動過程進行分析。

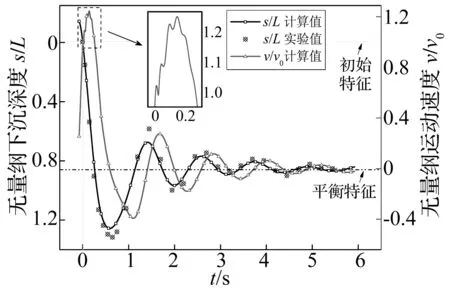
圖4　運動規律與速度變化規律Fig.4 Trajectory and velocity of the freely falling cylinder with an un-closed solid cavity as time

在入水下沉階段(0～0.62 s)，開口端以v0速度撞擊自由水面，由于撞水面積小，作用時間短，加之腔內氣體緩沖作用，導致殼體運動速度幾乎沒有衰減，運動軌跡未發生明顯改變；撞擊發生后，開放腔體被涌入的液體封閉，內部形成空氣彈簧，如圖中放大區域所示，在重力與氣體振動共同作用下，殼體運動速度呈現波動增加狀態，說明氣體振動對殼體運動產生了一定影響，但流體作用力相對重力依然較小，未能改變殼體運動趨勢；隨著入水深度增加，浮力迅速增大，在0.15 s時刻殼體到達平衡位置，速度達到最大值；對于正浮力殼體，浮力大于重力，經過平衡位置后殼體減速下沉，由于腔內氣體振動快速衰減，對運動的影響基本消失，速度曲線再次變得平滑，在0.62 s時刻速度衰減至零，殼體下沉至最深位置。

在起伏振蕩階段(0.62～5.88 s)，殼體由最深位置開始上浮，其完全沉浸于液體之中，此時殼體受到恒定浮力作用，但由于大量空泡脫落的影響，速度近似直線增加，于1 s時刻，殼體封閉端完成出水運動；出水后在變浮力的作用下，殼體下沉深度和運動速度皆呈現波動變化規律，且在黏滯阻力作用下幅值快速衰減，但頻率基本恒定。

圖5給出了空腔內涌入液體液面平均位置的變化情況及其與殼體運動間的關系，液面深度與殼體運動保持同步運動，其差值表征流入腔體內的液體體積，從圖中虛線框放大區域所示，在入水下沉過程中流入的液體逐漸增加，并表現出波動規律，即腔體內出現氣體漲縮，漲縮程度相對殼體振蕩較小，且僅出現在入水第一次下沉階段。在起伏振蕩階段，腔體內液面與殼體的運動幾乎同步，但由于慣性作用，僅在殼體沉至最深位置和浮至最高位置時出現相對運動，因此，在此階段由腔內氣體變化引起的浮力變化可以忽略。

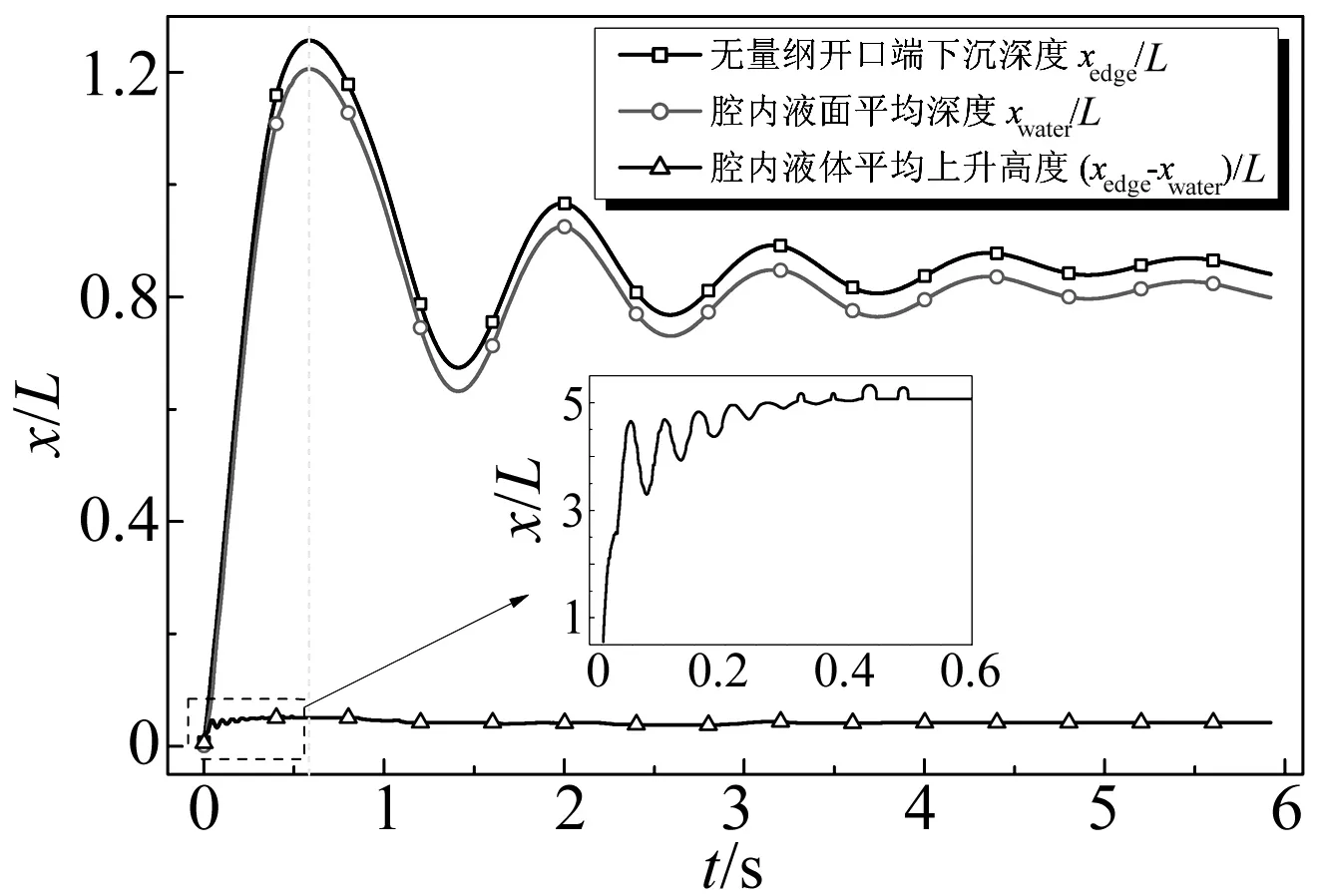
圖5　腔內液面平均位置變化規律Fig.5 The position of liquid in the solid cavity as time

3.2軸向作用力分析

入水過程中，作用在殼體軸線方向上的流體動力主要有壓差阻力和黏滯阻力。對于本文中的低速入水過程而言，黏滯阻力相對較小，本文未對其進行分析；壓差阻力作用在殼體封閉端內壁面和開口端面，由動壓力與靜壓力構成，同重力共同決定殼體的運動規律。

圖6給出了殼體封閉端內壁面和開口端面的壓力變化規律，其中以重力G為特征值對壓差阻力無量綱化處理。可見，撞水時刻兩面均受到沖擊，但沖擊力相對較小；隨著殼體下沉，壓力呈現波動增加過程，其中封閉端內壁面壓力波動較為劇烈且持續時間較長，下沉至最深位置后壓力波動消失；此后壓力值隨殼體起伏振蕩出現周期性波動，并與深度成正比關系。壓力波動是由于動壓作用引起的，其最終平衡值代表平均壓力，封閉端內壁面和開口端面上作用力之和為殼體浮力，平衡狀態其值與重力平衡，殼體實現漂浮。

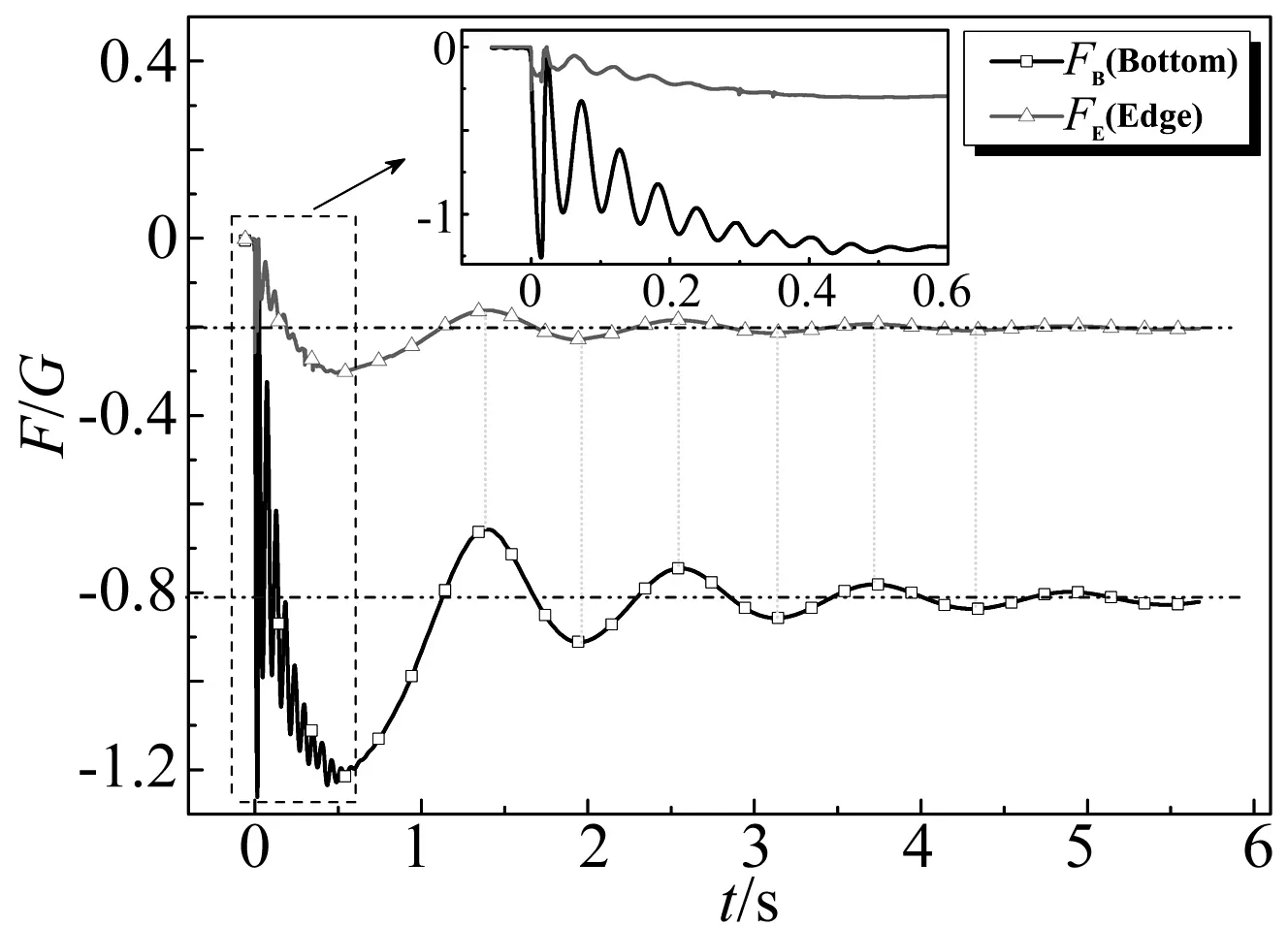
圖6　封閉端內壁面和開口端面壓力變化規律Fig.6 Hydrodynamic force for bottom and edge as time

為進一步分析入水過程中軸向力的構成和產生方式，通過濾波的方法，根據頻率的差異將封閉端內壁面受到的壓力分解為兩個壓力，圖7給出了兩種壓力的變化規律和擬合曲線，分別是由殼體運動引起的液體動壓和靜壓作用力Fm，稱作殼體運動作用力；和由腔體內氣體漲縮產生的氣體作用力Fv，稱作氣體漲縮作用力。兩種壓力變化均表現出明顯的有阻尼振動規律，分別對其進行擬合，壓力振動頻率分別為0.853 Hz和18.05 Hz。

對于殼體運動作用力，在撞擊液面前便出現初始壓力，撞擊后，沖擊力經氣體傳遞作用于封閉端，導致其上壓力迅速增加，但較短時間內便消失。此后，殼體開口端靜壓力隨著殼體浮沉波動變化，并通過腔體內流體介質施加于封閉端內壁面上(此時動壓力量級相對靜壓力較小)，其壓力波動與殼體振蕩同步，并最終平衡于0.8倍重力左右。殼體運動作用力是殼體軸向力的主要組成部分，其數值較大，并作用于入水全過程，對入水運動規律具有決定性作用。

對于氣體漲縮作用力，沖擊過程部分能量作用于腔內氣體，使氣體壓縮，液體流入將開口端封閉，腔體內部形成空氣彈簧。氣體漲縮作用在殼體封閉端產生一個同頻率變化的壓力，壓力振動頻率相對穩定，幅值衰減較快，在下沉至最深位置時完全耗散。氣體漲縮作用力僅作用在入水下沉階段，平均值為0 N，但撞擊后的短暫時間里，氣體漲縮作用力有效值相對較大且衰減較快，其不能決定入水運動趨勢，但對運動產生一定擾動。

因此，正浮力開放腔體圓柱殼入水運動是殼體自身的浮沉運動和腔體內氣體振動兩種運動的合成，前者表現為由下沉深度引起的靜壓作用和殼體運動導致的動壓作用，后者表現為由沖擊作用和空氣彈簧振動導致的周期性壓力作用。

導致氣體振動的原因主要是入水沖擊和氣體壓縮，這兩種物理過程的作用方式具有較大差異，造成氣體振動形式也略有不同。由于空腔內氣體的振動導致液體的吸入和排出，所以開口端質量流量變化可以準確反映開放腔體內部氣體振動，因此通過對比振動壓力與開口端質量流量的變化過程，進一步分析氣體振動特征及產生機理，并對上述對封閉端壓力拆分的正確性進行驗證。

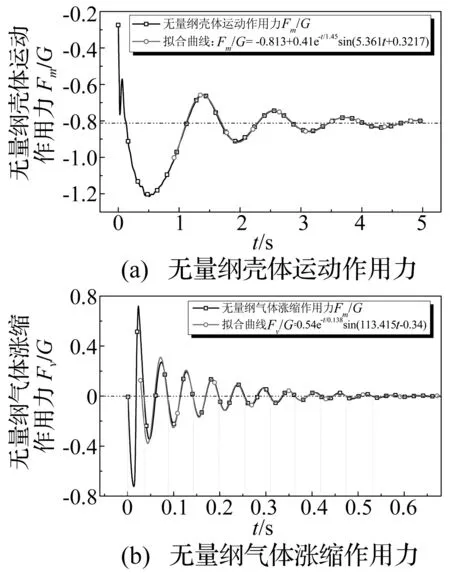
圖7　封閉端內壁面壓力 Fig.7 Pressuer of bottom by model movement and air shock

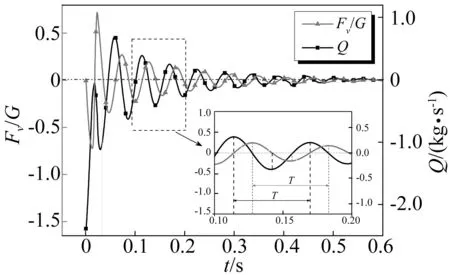
圖8　振動壓力與開口端質量流量變化Fig.8 Comparisons of the pressure by air shock between mass flow-rate in the open end

圖8給出振動壓力波動規律與開口端質量流量Q變化規律，定義撞擊液面后0.05 s時間為沖擊過程，開口端流入液體，腔體體積被壓縮，但從軸向力波動規律來看，在此期間腔內氣體已經開始振動，說明此時的振動并非氣體漲縮引起，而是入水沖擊造成的。圖9展示了沖擊過程腔體內壓力場分布，沖擊在開口端氣體產生瞬時高壓，局部氣體迅速壓縮，在腔體內形成高梯度分布的壓力，并向低壓區釋放，形成壓力脈沖，但沖擊過程劇烈且短暫，僅在局部造成壓力場突變，腔體內部出現壓力振蕩，在封閉端表現出壓力波動；壓力脈沖同時也作用于上升的液面，使開口端質量流量隨壓力波動擴散而驟減，壓力波動收縮而激增。沖擊后較短時間(0.03 s左右)腔體內部壓力便趨于一致，在慣性力作用下，大量液體流入下沉的腔體，腔體內部壓力將大于開口端環境壓力，當達到最大壓縮量后，氣體開始膨脹，實現氣體振動。此時封閉端內壁面的壓力主要由氣體整體壓縮振動引起，其振動幅值大幅減小，僅為沖擊壓力的3/7，振動頻率略有降低。如圖8中放大區域所示，在振動趨于穩定后，兩種振動具有相同的振動頻率，間隔π/2弧度的相位角，實現腔體內液體與氣體實現同步振動，其中開口處質量流量反映氣體振動速度變化規律，振動壓力反映氣體振動的回復力變化規律。

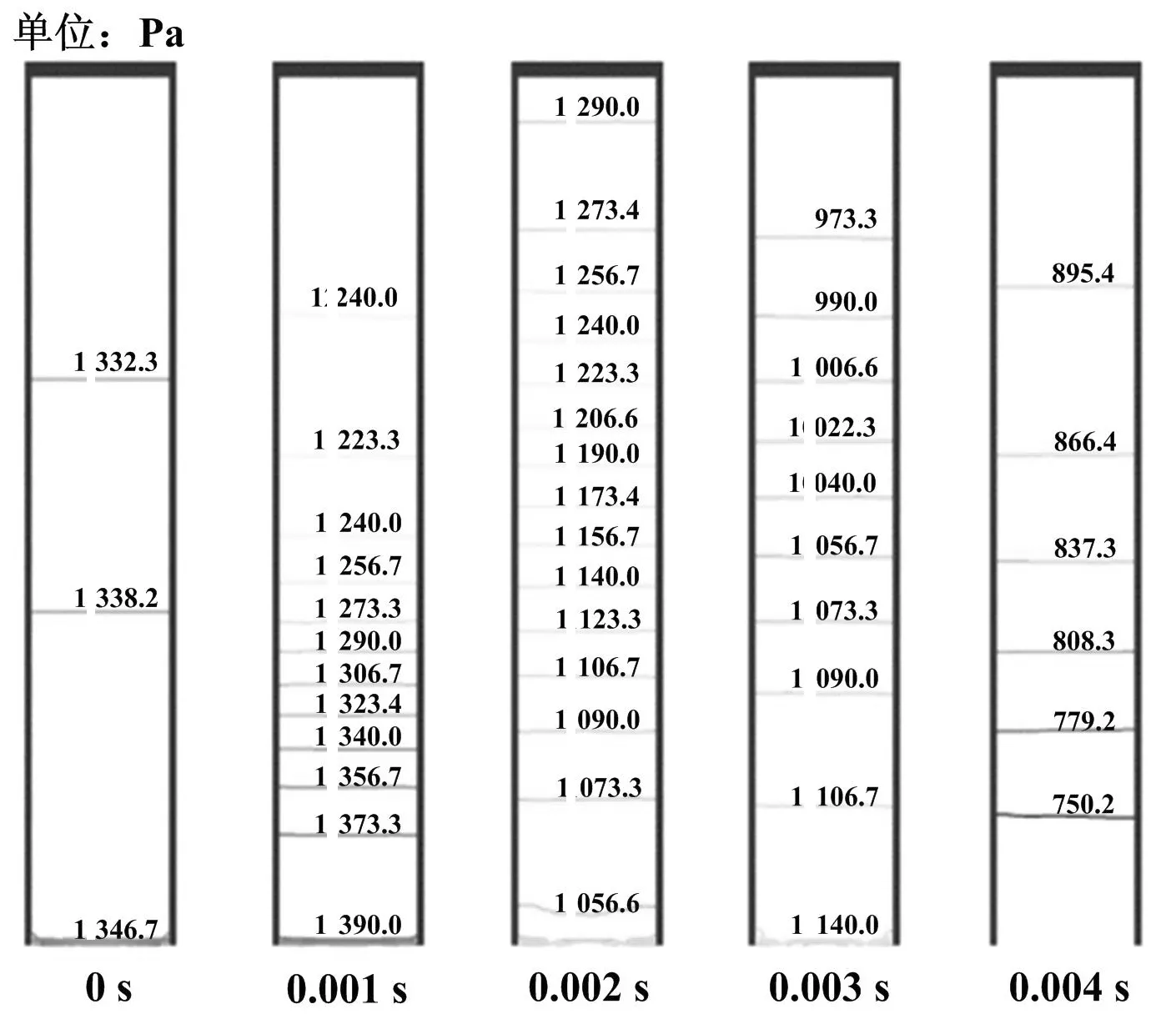
圖9　腔體內部壓力場分布Fig.9 Pressure contours inside the solid cavity at different time

3.3殼體壁面壓力分布

殼體通常為薄壁結構，易受到徑向作用力而發生畸變，特別是入水過程伴隨大沖擊及空泡潰滅產生的高壓作用，因此對殼體壁面壓力分布及變化的研究具有實際意義。

圖10展示了殼體外壁面表面壓力分布及變化規律，在首次下沉過程中開口端出現一個低壓區，對應于入水空泡區域(泡內壓力恒定且低于環境壓力)，并在空泡潰滅處形成壓力峰值，壓力峰值位置隨時間出現脈動，脈動致使壁面形成脊狀壓力，并延著軸向向封閉端傳遞，但壓力峰值后壓力大體呈現梯度分布；殼體下沉至最深位置后，空泡全部脫落，低壓區域消失，壁面處于靜壓力場中，隨殼體起伏振蕩壁面壓力出現同頻率波動。通過上述分析可知，殼體外壁面受到的平均壓力較小，并在后續振蕩過程中呈遞減趨勢，空泡閉合造成的壓力峰值同樣較小，壁面上壓力未出現極大峰值，因此低速入水過程中壁面壓力不會對結構造成破壞。

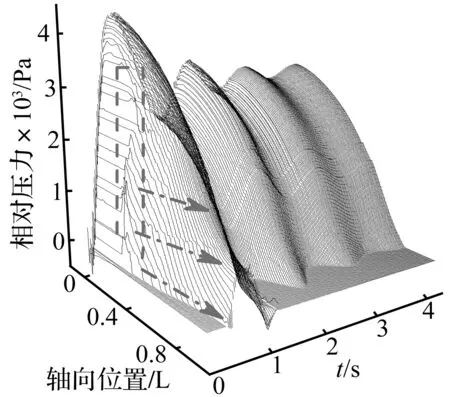
圖10　殼體外壁面表面壓力分布及變化規律Fig.10 Pressure distribution and variation on the outside surface

3.4空泡形態發展規律

入水空泡將有效地改善殼體流體動力環境，因此對于入水空泡演化研究極其必要。圖11展示了入水空泡生成、發展及潰滅過程，撞擊液面后在殼體肩部生成入水空泡，空泡快速收縮，腔內氣體振動對空泡直徑產生影響，殼體肩部空泡直徑增大，并沿殼體軸向向水面傳遞，造成空泡壁的周期波動，其波動周期在0.04 s左右，與前文分析的腔內空氣振動周期相符；0.08 s時刻肩部空泡完成閉合，在開口端形成獨立的空泡，隨著下沉靜水壓力增大，迫使空泡開始收縮，在靜水壓力與慣性力平衡點處出現頸縮，空泡出現斷裂分離，殼體在達到最深位置處，肩部空泡基本全部脫落，但部分氣泡仍然附著于殼體壁面；在殼體上浮過程中部分氣泡重新融合，封閉端沖破尾空泡完成出水過程，最終空泡全部潰滅。

圖11　入水空泡形態演化Fig.11 Water-entry cavity development

從能量的角度對入水空泡發展進行分析，沖擊將殼體動能傳遞給周圍流域，流體獲得動能后形成流動，流體動能轉化為周圍流場勢能，使液體向外側排開形成入水空泡；對于本文中開放腔體模型而言，撞擊傳遞給流域的能量較小，后續的動能又大部分用于壓縮腔內氣體，轉化成為氣體彈性勢能，因此入水空泡相對較小；腔內氣體獲得足夠能量后開始振動，氣體振動使開口端以相同頻率吸入排出液體，使周圍流場獲得動能，產生周期性振蕩，由于空泡自身勢能較小，在周圍流場擾動影響下，空泡壁面產生同頻率波動現象，同時加速了空泡脫落過程。

4　結　論

本文對具有正浮力特性及開放腔體結構的圓柱型殼體低速垂直入水過程開展了三維數值仿真，對運動規律、流體動力特征、壁面壓力分布及入水空泡的發展規律進行了研究，具體結論如下：

(1) 殼體完成入水下沉后，在正浮力特性作用下，殼體將出現上浮-出水-再下沉周期交替的振蕩運動過程；開放腔體不會影響整體運動趨勢，僅對入水下沉階段的運動產生一定擾動。

(2) 對運動全過程而言，軸向壓差阻力與下沉深度成正比，運動導致的靜壓和動壓是壓差阻力的主要組成部分；在入水下沉階段軸向力出現高頻振動，但幅值較小、衰減較快，下沉至最深位置處完全消失。

(3) 入水后開放腔體形成了獨立空間，入水沖擊使腔體內局部氣體壓縮、引起壓力振蕩；隨著液體流入，腔內氣體壓縮震蕩，對封閉端產生周期性附加流體動力；氣體流動消耗了大量沖擊能量，使封閉端受到的沖擊力減小，腔體起到了緩沖作用；氣體振動導致開口端周期地吸入-排出液體，形成了惡劣的流域環境。正浮力開放腔體圓柱殼入水運動是其自身的浮沉運動與腔體內氣體振動的合成。

(4) 入水空泡體積較小，僅對開口端部分實現了包裹，并較早完成了空泡閉合；腔體內氣體振動的對流體動力產生較大的影響，使空泡壁面出現明顯的波動現象，加速空泡的脫落和潰滅；脫落的空泡在上浮過程中融合，但對殼體出水及后續運動未有明顯影響。

通過本文的研究，開放腔體的殼體入水具有獨特的運動特征及流體動力特征，特別是腔體內部流場運動比較復雜，本文僅通過數值方法對垂直低速入水過程進行了初步研究，此問題還有大量工作需要進一步開展，希望本文能為后續研究奠定一定基礎。

[1] MASON D R, FOLKMAN S L, BEHRING M A. Thrust oscillations of the space shuttle solid rocket booster motor during static tests[J]. AIAA Paper, 1979, 79(1138): 18-20.[2] 別社安，趙沖久，及春寧，等. 筒型基礎海洋平臺氣浮拖航穩性分析[J]. 天津大學學報，2002，35(2)：221-225.

BIE Shean, ZHAO Chongjiu, JI Chunning, et al. Stability analysis of the bucket foundation platform transported by air floating[J]. Journal of Tianjin University, 2002, 35(2): 221-225.

[3] DE BACKER G, VANTORRE M, BEELS C, et al. Experimental investigation of water impact on axisymmetric bodies[J]. Applied Ocean Research,2009,31(3):143-156.[4] WORTHINGTON A M. Impact with a liquid surface studied with aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society of London, 1900, 194A: 175-199.

[5] HERTING D N, POHLEN J C, POLLOCK R A. Analysis and design of the Apollo landing impact system [C]//Proceedings of the AIAA and NASA Third Manned Space Flight Meeting. Houston, USA, 1964.

[6] BENSON H E. Water impact of the Apollo spacecraft [J]. Journal of Spacecraft and Rockets, 1966, 3(8): 1282-1284.

[7] MAY A, WOODHULL J C. Drag coefficients of steel spheres entering water vertically[J]. Journal of Applied Physics, 1948, 19(12): 1109-1121.

[8] MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically[J]. Journal of Applied Physics,1950,21(12):1285-1289.

[9] MAY A. Effect of surface condition of a sphere on its water-entry cavity[J]. Journal of Applied Physics, 1951, 22(10): 1219-1222.

[10] MAY A. Review of water-entry theory and data[J]. Journal of Hydronautics, 1970, 4(4): 140-142.

[11] GEKLE S, VAN DER BOS A, BERGMANN R, et al. Noncontinuous froude number scaling for the closure depth of a cylindrical cavity[J]. Physical Review Letters, 2008, 100(8): 084502.

[12] YAN H, LIU Y, KOMINIARCZUK J, et al. Cavity dynamics in water entry at low Froude numbers[J]. Journal of Fluid Mechanics, 2009, 641: 441-461.

[13] HE C, WANG C, WEI Y, et al. Numerical simulation of pressure distribution in vertical water-entry cavity[J]. Journal of Ship Mechanics, 2011,15(9):960-968.

[14] 何春濤，王聰，何乾坤，等. 圓柱體低速入水空泡試驗研究[J]. 物理學報，2012，61(13)：134701-134701.

HE Chuntao, WANG Cong,HE Qiankun,et al. Low speed water-entry of cylindrical projectile[J]. Acta Physica Sinica,2012, 61(13): 134701.

[15] BROOKS J R, ANDERSON L A. Dynamics of a space module impacting water[J]. Journal of Spacecraft and Rockets, 1994, 31(3): 509-515.

[16] 趙蛟龍，孫龍泉，張忠宇，等. 柱形空腔結構落水載荷及沖擊響應研究[J]. 振動與沖擊，2013，32(20)：113-118.

ZHAO Jiaolong，SUN Longquan，ZHANG Zhongyu，et al. Hydrodynamic loads and impact response for a water entry of a cylindrical cavitary structure[J]. Journal of Vibration and Shock, 2013, 32(20): 113-118.

Numerical study on vertical water-entry of a cylindrical structure with positive buoyancy and un-closed solid cavity

LU Zhonglei, WEI Yingjie, WANG Cong, CHEN Chen

(School of Astronautics, Harbin Institute of Technology，Harbin 150001, China)

The water-entry impact on the open end of a cylindrical structure with un-closed solid cavity causes air compression and oscillation in the cavity. The coupling between air vibration and structure movement leads to some special flow phenomena. Based on the homogeneous equilibrium flow theory, a three-dimensional numerical simulation was carried out to study the vertical water-entry process. The structure used in the simulation was a cylindrical shell with positive buoyancy and un-closed solid cavity. The results show that the un-closed solid cavity plays a buffering action. Air movement in the solid cavity can be divided into two processes: the oscillations caused by impact and compressing respectively. Air vibration has high frequency, low amplitude, and fast attenuation properties, and brings a disturbance to the shell movement at the sinking period. The open end of the shell inhales and ejects liquid at the same frequency, which lead to a complex fluid field environment. The cavitation wall waves and the cavitation collapse early.

water-entry; un-closed solid cavity cylinder; positive buoyancy; numerical simulation

黑龍江省自然科學基金(A201409);哈爾濱市科技創新人才研究專項資金項目(2013RFLXJ007)

2015-07-02修改稿收到日期：2015-09-06

路中磊 男，博士生，1985年生

魏英杰 男，博士，教授，博士生導師，1975年生

TB126；V19

A

10.13465/j.cnki.jvs.2016.16.014