兩自由度磁力懸浮非線性振動能量采集研究

王祖堯, 丁　虎， 陳立群, 3

(1.上海大學 上海市應用數學和力學研究所，上海　200072；2. 浙江科技學院 理學院，杭州　310023； 3. 上海大學 力學系，上海　200444)

?

兩自由度磁力懸浮非線性振動能量采集研究

王祖堯1, 2, 丁虎1， 陳立群1, 3

(1.上海大學 上海市應用數學和力學研究所，上海200072；2. 浙江科技學院 理學院，杭州310023； 3. 上海大學 力學系，上海200444)

首次研究通過增加自由度數，擴大磁力懸浮非線性能量采集器的采集區域。通過引入線性彈簧振子，將單自由度非線性磁力懸浮能量采集器擴展到兩個自由度。使用諧波平衡法近似分析兩自由度非線性常微分方程組，研究位移激勵下系統主共振的穩態幅頻響應特征。研究結果表明，兩自由度系統能夠顯著擴展系統的共振區域。還通過對比系統各個參數對共振幅頻響應幅度以及區域的影響，研究了系統質量比、頻率平方比和非線性系數比對增強共振強度、擴大共振區域，也就是提高能量采集的強度和帶寬的影響。另外，還通過直接的數值模擬驗證了近似解析分析結果的正確性。

非線性；振動；磁懸浮；能量采集；諧波平衡

現代科技中，無線電子設備在生物醫學設備、計算機系統、便攜式電子產品、以及導航系統等領域都有著廣泛的應用。這些無線設備中多是使用電池作為其電源，而更換電池和處理廢舊電池都需要額外增加使用費用。而另一個方面，隨著超大規模集成電路設計的水平提高,無線電子設備的功耗從毫瓦數量級降低到微瓦數量級。因而，振動能量采集器為這種無線設備提供電源就成為可能。國內外許多研究人員已經對這種微機系統提供電源的振動能量采集進行研究[1-5]，力圖提高振動能量的采集的效率和擴大采集的頻率范圍。JIANG等[6]研究了單穩態的能量采集器在高斯白噪音激勵下的能量采集的強度。也有一些學者試圖從多穩態的能量采集的角度增加能量采集的強度[7-9]。這些研究都發現，引入非線性因素能夠增加能量采集的帶寬。通過非線性磁力作用，ZHU等[10]提出了一種新型的磁懸浮能量采集器，實驗表明這種設計可以增加能量的采集強度并擴展采集的頻帶寬度。MANN等[11]通過單自由度彈簧振子的非線性振動特性分析，對這種磁懸浮的裝置的非線性能量采集性能進行了近似解析分析，得到了幅頻響應關系，從理論上分析了這種非線性能量采集原理。

本文在文獻[10-11]的能量采集裝置中增加了一個線性彈簧振子，便于調節非線性振動能量采集的頻率。進一步建立兩自由度非線性振動方程組，通過諧波平衡方法研究了該強非線性系統在外部簡諧位移激勵下的穩態響應特征[12-15]。并通過直接數值方法加以驗證。研究發現增加線性彈簧振子，能夠有效的改變磁力懸浮的非線性振動能量采集器的動力學響應，并進一步提高能量采集的強度和帶寬。通過對比不同參數的系統響應，研究了系統各參數對能量采集效果的影響。

1　磁懸浮非線性能量采集系統建模

磁懸浮振動型能量采集系統工作原理見圖1和圖2，兩個磁體固定在支柱上的兩端，支柱中間再插進一磁體，其下方懸掛一個彈簧振子。上下磁體兩極的磁力使中間磁體可以懸浮在中間。當該系統在外部諧波激勵下，中間磁體就產生非線性振動，并且改變Terfenol-D/PZT/Terfenol-D層壓復合材料的周圍磁場。由于Terfenol-D具有磁振效應，Terfenol-D的形狀被改變。Terfenol-D和PZT足夠牢固造成PZT也隨著振動。PZT具有壓電效應，在PZT形狀尺度的改變時就產生了電流。

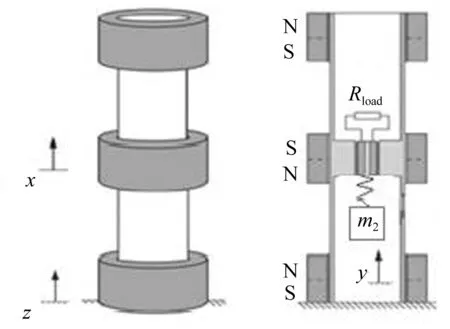
圖1　磁力懸浮能量采集系統圖Fig.1 A illustration of the magnetic levitation energy harvesting system

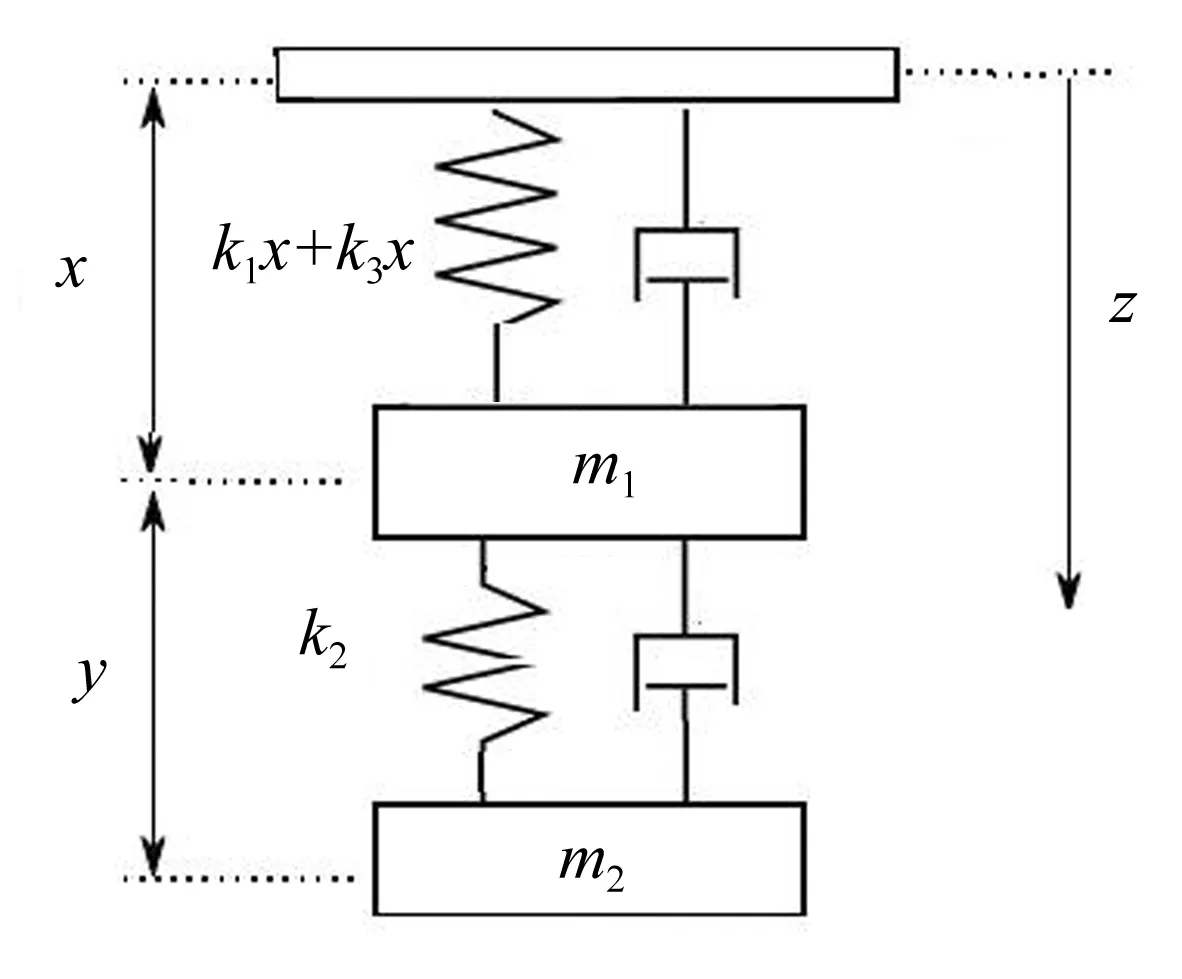
圖2　磁力懸浮能量采集系統的力學模型圖Fig.2 A mechanical model schematic of the magnetic levitation energy harvesting system

由于磁力的密度取決于中間磁體與兩端磁體的距離，而距離的求解可以通過系統的控制方程得到。考慮非線性磁力、重力、阻尼和根據牛頓第二定律可以得到系統的運動方程:

(1)

2　諧波平衡法分析

由于圖1所示的能量采集裝置是一個強非線性系統，這里通過諧波平衡法對式(1)進行近似求解。為了將分析的問題一般化，首先對式(1)進行無量綱化處理，即取如下所示無量綱參數

(2)

將以上無量綱參數代入控制方程式(1)，可以得到如下無量綱化的控制方程

(3)

假設式(3)的解滿足如下形式

(4)

將式(4)代入式(3)，并令常數項cosωt和sinωt的系數分別相等，得到下列方程

a10+βa103+a1-μf2a20+

(5)

(1+μ)f2a20-a10-βa103-

(6)

μωfγ2a21-μf2b21-p=0

(7)

+μωfγ2b21-μf2a21=0

(8)

-ω2b21+(1+μ)fωγ2a21+

(1+μ)f2b21-γ1ωa11-b11-

(9)

-ω2a21-(1+μ)fωγ2b21+(1+μ)f2a21+γ1ωb11-

(10)

對于給定的激勵頻率ω，通過求解式(5)～式(10)，可以解得a10,a20,a11,a21,b11,b21。從而可以分別求得中間磁鐵和彈簧振動的振幅，即

(11)

3　系統參數對幅頻響應的影響

為研究新引入彈簧振子對磁力懸浮能量采集系統的幅頻響應的影響，選取如下系統參數[10]:m1=0.012 g，c1=0.1 Ns/m，線彈性項系數k1=6.39 N/m，非線性彈性系數項k3=166 000 N/m3，外激勵位移W=0.011 5 m，c2=0.01 Ns/m，彈簧系數k2=0.01 N/m，m2=0.012μg，其中μ是彈簧懸掛質量與中間磁鐵的質量比值。

3.1二自由度的質量比的影響

接下來先運用諧波平衡法，計算在不同的質量比μ下磁力懸浮能量采集系統的幅頻響應。如圖2所示，當μ=0.05時，磁力懸浮能量采集系統的幅頻響應類似單自由度的幅頻響應，即僅存在一個共振峰。其原因是懸掛的振子質量過小，可以忽略不計。此時，中間磁鐵的振動幅度在ω=2.0～2.5之間達到峰值。當μ=1和1.5時，中間磁鐵的穩態響應振幅都在ω=1.0附近和ω=3.5附近時，出現兩個共振峰。而且第二個共振峰的幅度超過了單峰時的共振幅度。另外，從圖3可知，質量比越大，第一個共振峰的幅值越小，但是第二個共振峰的幅值同時在增大。還需要指出，質量比越大，兩個共振峰之間距離越大。

圖4給出μ=1時四階龍格庫塔法的直接數值結果與諧波平衡法近似分析結果的對比。觀察發現，通過數值方法得到的中間磁鐵的振幅與諧波平衡法得到中間磁鐵的振幅基本吻合。

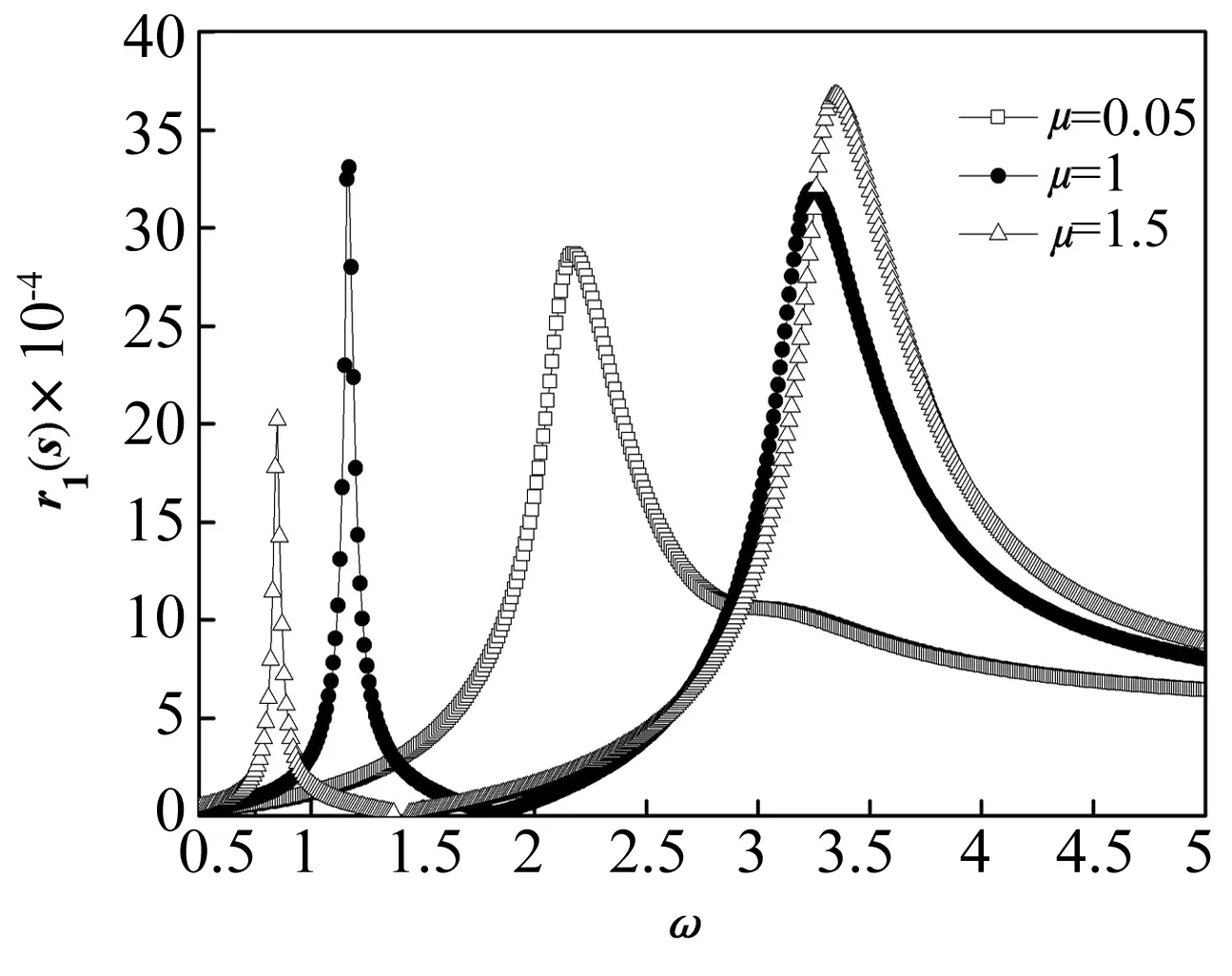
圖3　在不同質量比下的中間磁體幅頻頻響應Fig.3 Frequency response of middle magnet as the mass ratio μ changes

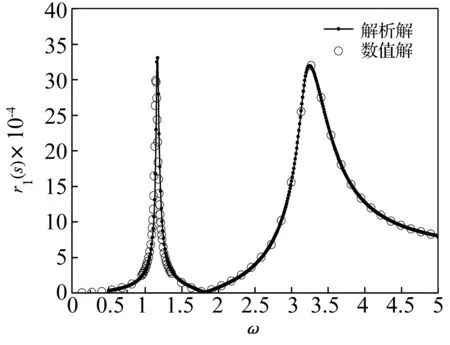
圖4　中間磁鐵幅頻響應的數值驗證(質量比μ=1)Fig.4 Numerical verification for the frequency response of middle magnet as the mass ratio μ=1

3.2兩自由度的頻率比的影響

接下來研究兩自由度系統前兩階固有頻率比值對磁力懸浮能量采集系統能量采集效果的影響。選取質量比的μ=1。為了方便起見，選取固有頻率比的平方分別為6、9和16。在選取頻率比和其他參數的條件下，可以求得懸掛彈簧線彈性系數k2。

如圖5所示，當頻率比的平方比取為9時，中間磁鐵穩態幅頻響應的第一個共振峰幅值要比頻率平方比取為6和16時的第一個峰值大，與此同時，第二個共振峰的峰值要比其他的峰值小。因此，可以通過調節兩自由度之間的頻率比，改變共振區域和強度，并到達強化某一階主共振的目的。從而提高系統對振動能量采集的效果。

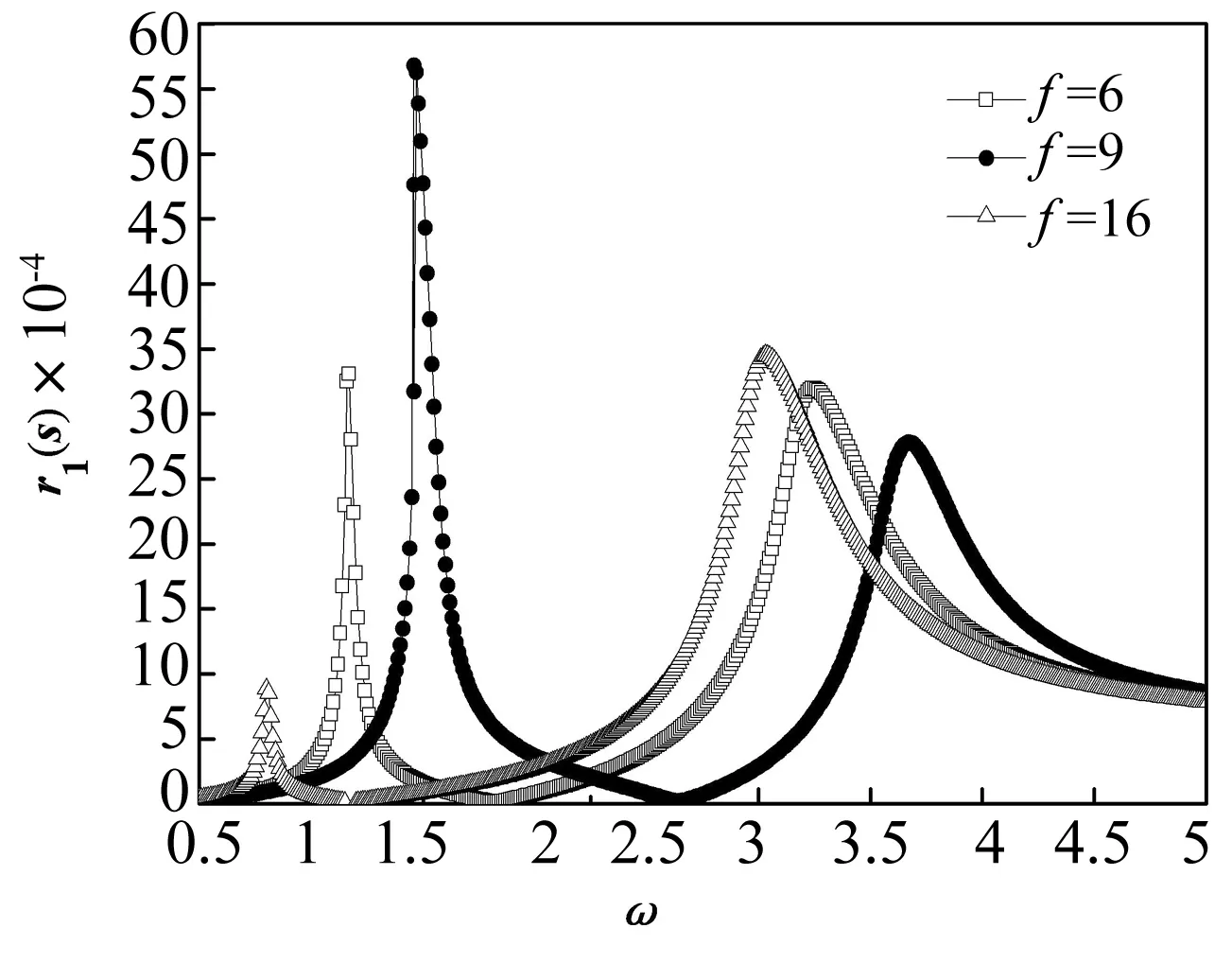
圖5　中間磁鐵在不同頻率比的平方下的幅頻頻響應Fig.5 Frequency response of middle magnet as the tuning square ratio f changes

3.3非線性系數的影響

選取兩自由度質量分別為m1=0.012 g和m2=0.012 g。并選取非線性彈性系數k3=166 000 kN/m3。圖6給出了k取為1、6和10時，中間磁鐵的穩態幅頻響應曲線。觀察圖6發現，非線性彈簧系統的取值對第一階主共振的位置影響不大，但是非線性系統較小時，第一階共振峰的峰值較高。另一個方面，非線性系統對第二階共振的影響更為顯著，不但會影響共振區域，較大的非線性系數還會增強第二階共振峰峰值。

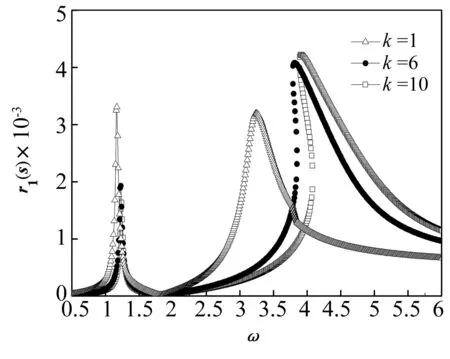
圖6　中間磁鐵在不同的非線性系數比k下的幅頻響應Fig.6 Frequency response of middle magnet as the nonlinear coefficient ratio k changes

4　結　論

通過在已存在的一種磁力懸浮非線性能量器采集系統中增加一個線性彈簧振子，本文的研究表明，新增振子能夠很大程度上改變系統的動力學特性。通過受力分析建立兩自由度的非線性振動控制方程。通過諧波平衡法的近似解析分析和直接數值方法的驗證研究了該能量采集系統在簡諧位移激勵下的穩態輻頻響應。研究表明，系統的響應從單共振峰演化為該單峰兩邊的兩個共振峰，因此增大了能量采集的頻帶寬度。另外，通過參數分析發現，調節系統參數，可以方便的增強兩個共振峰的中任意一個，以達到增強振動能量采集效果的目的。

[1] 胡長德, 趙美蓉, 劉穎偉,等. 壓電微懸臂梁共振頻率的檢測系統[J]. 壓電與聲光, 2009, 31(6): 935-938.

HU Changde,ZHAO Meirong, LIU Yingwei, et al.Resonance frequency detection of piezoelectric micro-cantilever[J]. Piezoelectrics & Acoustooptics,2009, 31(6): 935-938.

[2] 袁江波,謝濤,陳維山,等. 懸臂梁壓電發電裝置的實驗研究[J]. 振動與沖擊, 2009, 28(7): 69-72. YUAN Jiangbo, XIE Tao, CHEN Weishan,et al. Experimential study on piezoelectric generator with cantilever [J]. Journal of Vibration and Shock, 2009, 28(7): 69-72.[3] 陳仲生, 楊擁民. 懸臂梁壓電振子寬帶低頻振動能量俘獲的隨機共振機理研究[J]. 物理學報, 2011, 60(7): 074301.

CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wide band and low frequency vibration energy harvesting based on piezoelectric cantilever beams [J]. Acta Physica Sinica, 2011, 60(7): 074301.

[4] 劉海利, 徐天柱, 黃震宇, 等. 基于諧振器的多模態壓電換能結構研究[J]. 振動工程學報,2011,24(5):491-497.

LIU Haili, XU Tianzhu, HUANG Zhenyu, et al.A piezoelectric cantilever with an oscillator for multi-mode vibration energy harvesting [J]. Journal of Vibration Engineering, 2011, 24(5): 491-497.

[5] DAI Xianzhi, WEN Yumei, LI Ping, et al. Modeling characterization and fabrication of vibration energy harvester using Terfenol-D/PZT/Terfenol-D composite transducer [J]. Sensors and Actuators, 2009, 156: 350-358.

[6] JIANG Wenan, CHEN Liqun. Energy harvesting of monostable Duffing oscillator under Gaussian white noise excitation [J]. Mechanics Research Communications, 2013, 53: 85-91.

[7] ZHOU Shengxi, CAO Junyi, INMAN D J, et al. Broadband tristable energy harvester: modeling and experiment verification [J]. Applied Energy, 2014, 133: 33-39.

[8] WU Z, HARNE R L, WANG K W. Harvester synthesis via coupled linear-bistable system with multistable dynamics [J]. Journal of Applied Mechanics,2014,81:0610051-0610059.

[9] JIANG Wenan, CHEN Liqun.Snap-through piezoelectric energy harvesting [J]. Journal of Sound and Vibration, 2014, 333(18): 4314-4325.

[10] ZHU Yang, ZU J W, GUO L. A magnetoelectric generator for energy harvesting from the vibration of magnetic levitation [J]. IEEE Transactions on Magnetics,2012,48(11):3344-3347.

[11] MANN B P, SIMS N D. Energy harvesting from the nonlinear oscillations of magnetic levitation [J]. Journal of Sound and Vibration, 2009, 319: 515-530.

[12] 陳立群, 吳哲民. 多自由度非線性振動分析的平均法. [J].振動與沖擊,2002,21(3):63-65.

CHEN Liqun, WU Zhemin. Averaging method for analyzing a multi-degrees of freedom[J]. Journal of Vibration and Shock, 2002, 21(3): 63-65.

[13] 黃坤, 馮奇. 非對稱截面兩自由度非線性振動[J]. 振動與沖擊, 2012, 31(8): 80-85.

HUANG Kun, FENG Qi. Non-linear vibration of two-degree-freedom for a non-symmetrical cross-section[J]. Journal of Vibration and Shock, 2012, 318(8): 80-85.

[14] 胡輝, 郭源君, 鄭敏毅.一個非線性奇異振子的諧波平衡解[J]. 振動與沖擊, 2009, 28(2): 120-123.

HU Hui, GUO Yuanjun, ZHENG Minyi. Harmonic balance approaches for a non-linear singular oscillator[J]. Journal of Vibration and Shock, 2009, 28(2): 120-123.

[15] 賈尚帥, 孫舒, 李明高. 基于諧波平衡法的雙穩態壓電發電系統非線性振動特性研究[J]. 振動與沖擊,2014,33(6): 170-173.

JIA Shangshuai, SUN Shu, LI Minggao. Non-linear vibration analysis of bistable piezoelectric power generation system based on harmonic balance method[J]. Journal of Vibration and Shock, 2014, 33(6): 170-173.

Nonlinear oscillations of a two-degree-of-freedom energy harvester of magnetic levitation

WANG Zuyao1,2, DING Hu1, CHEN Liqun1,3

(1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2. School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China;3. Department of Mechanics, Shanghai University, Shanghai 200444, China)

For enlarging the area of magnetic levitation nonlinear energy harvesting, the paper studied the nonlinear dynamics of a two-degree-of-freedom nonlinear energy harvester of magnetic levitation for the first time. A one-degree-of-freedom nonlinear energy harvester of magnetic levitation was expanded by introducing an linear oscillator. The nonlinear ordinary differential equations were approximately analyzed by using the harmonic balance method. Under the displacement excitation, the characteristics of the steady-state amplitude-frequency response of the primary resonance was studied. The results show that the resonance area of the two-degree-of-freedom system is significantly expanded. Moreover, by comparing the various parameters on the amplitude-frequency response and the resonance area, the effects of the mass ratio, frequency square ratio and nonlinear coefficient ratio on resonance are investigated. Therefore, the influences of the intensity of energy acquisition and the bandwidth are determined. In addition, the approximate analytic results are verified through a direct numerical simulation.

nonlinearity; vibration; magnetic levitation; energy harvesting; harmonic balance

國家自然科學基金重點項目(11232009); 國家自然基金面上項目(11372171); 國家自然基金優青項目(11422214)

2015-06-23修改稿收到日期：2015-08-28

王祖堯 男，博士生，1969年生

丁虎 男，博士，教授，博士生導師，1978年生E-mail: dinghu3@shu.edu.cn

O322

A

10.13465/j.cnki.jvs.2016.16.010