一種陣列天線快速波束賦形方法

王　力，何丙發，孫慶鋒

(南京電子技術研究所，　南京 210039)

?

·天饋伺系統·

一種陣列天線快速波束賦形方法

王力，何丙發，孫慶鋒

(南京電子技術研究所，南京 210039)

介紹了一種陣列天線快速賦形方法，該方法基于Orchard綜合，采用遺傳算法對Schelkunoff單位圓零點的位置移動實現波束賦形。波束賦形分為兩個步驟：1)根據副瓣電平采用解析法確定初始零點位置；2)以賦形區域內零點徑向位移作為自由度，用遺傳算法進行賦形區域單目標尋優。相對常見以陣元的幅度相位作為自由度編碼的遺傳算法賦形，該方法不僅有效避免了副瓣和賦形區的多目標均衡問題，而且算法自由度大幅減少，收斂速度快，能夠同時實現較低副瓣電平和賦形區精度要求。通過余割平方賦形和扇形波束兩個實例說明該方法的有效性，可以應用于陣列天線快速賦形設計。

波束賦形；Orchard綜合；遺傳算法

0　引　言

在雷達、通信等領域中，往往需要特殊形狀的天線波束賦形。根據波束形狀求解陣列天線單元間距、激勵的幅度和相位稱為天線綜合。這是天線設計過程中一個非常重要的環節。

實現波束賦形常見方法為解析法和各類搜素算法。解析法包括傅里葉變換法和Woodward綜合法等[1]。傅里葉變換法是綜合方向圖最直接的方法，但是這種方法需要獲得目標方向圖的解析表達式，求解困難。Woodward綜合法也被稱作零點填充法，在賦形區域能較好逼近預期方向圖，但在非賦形區域卻不能控制副瓣電平。

除了解析法，各類搜索算法也逐漸被天線設計所采用。Powell算法[2]等直接搜索算法思路簡單、計算速度快，然而屬于局部尋優算法，尋優能力受限。除此以外，智能搜索算法由于其全局搜索特性得到廣泛應用，典型的搜索算法包括遺傳算法[3]和粒子群算法[4]以及基于上述算法的改進[5-6]。

遺傳算法是20世紀60、70年代由Holland等人提出的一種全局優化算法，通過模擬生物進化過程尋找最優解，本質上是一種高度并行、隨機、自適應全局搜索方法。遺傳算法簡單通用、穩健性強，適用于處理傳統搜索方法難于解決的復雜和非線性問題，近年來，在天線陣列的設計中有較多應用。

采用遺傳算法實現天線波束賦形時，通常采用所有陣元的激勵幅度和相位作為自由度進行編碼，方向圖中賦形與副瓣等區域需要分別滿足誤差與副瓣電平等多個目標。因此，存在如下問題：(1)變量自由度為陣元數目的2倍，當陣元數目較多時，計算速度明顯減慢；(2)多目標優化容易陷入局部收斂，造成單目標占優；(3)低副瓣難以控制，當副瓣低于-30dB時，實際副瓣電平小于主瓣電平的1/1 000，陣元的幅相微小擾動就會造成副瓣較大起伏，因此副瓣進一步降低的程度有限。

為了解決上述問題，本文提出了一種新的零點優化算法。該方法基于Schelkunoff單位圓零點以及Or-chard綜合[7]，以滿足副瓣要求零點分布作為初始值，賦形區域內的零點沿單位圓徑向位置變化作為自由度，采用遺傳算法進行賦形優化。本方法有如下優勢：副瓣目標由初始值實現，自由度顯著減少，多目標函數簡化為僅僅賦形區域單目標函數，求解空間縮小，收斂速度加快，賦形精度明顯提高，可廣泛應用于各類賦形天線設計中。

1　優化方法

1.1Schelkunoff單位圓

Schelkunoff方法是天線陣列方向圖綜合中的一種經典方法，可以在方向圖的指定位置產生零深。相比于其他綜合方法，這是一種更深入實質的波束方向圖綜合技術。

由N個陣元均勻分布構成的一維天線陣列陣因子可以寫成

(1)

式中：In為第n個陣元的電流激勵系數，具有復數形式；k=2π/λ為波束。在式中作變換u=sinθ，z=exp(jkdsinθ)，于是，陣列多項式可以寫為

(2)

以上多項式有N-1個復數根，通過因式分解得到

(3)

不妨令IN=1，并不影響方向圖特性，因此陣列因子的幅值可以簡化為

(4)

式中：zn=exp(jkdsinθn)，限制在單元圓上的復平面上的點，決定了方向圖中零點的位置。陣列因子的幅度等于單位圓上的點z=x+jy與各零點zn直線線段長度的乘積，如圖1a)所示。通過控制單位圓上的零點位置，增加主瓣寬度，降低副瓣電平。

Orchard等人提出了一種新的方向圖綜合技術，增加了零點位置的自由度，由單位圓擴展到了單元外(內)，零點還可以沿單位圓徑向自由移動，自由度由θn增加為(θπ, rn)，此時，zn=rnexp(jkdsinθn)，將式(4)展開后求得系數即為陣元的電流激勵。Orchard零點控制的優勢在于能夠靈活控制每個起伏電平或者副瓣電平。

圖1b)為將副瓣區域內任意兩個零點移至單位圓外后的方向圖。從圖中可以看出，增加零點自由度后，不僅可以改變副瓣電平，而且可以任意改變主瓣或者副瓣的形狀，由此方向圖可以分為賦形區和副瓣區兩個部分：副瓣區域N1個零點被限制在單位圓上，賦形區域N2個零點自由移動，方向圖由N1+2N2個變量決定，通過各類算法即可求得最優方向圖和零點位置，最終將多項式展開得到每個陣元的幅相分布。

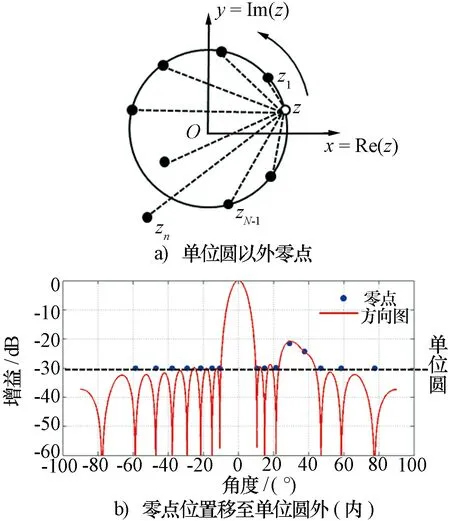
圖1　單位圓零點位置及方向圖綜合

1.2遺傳算法

遺傳算法中包含了如下四個基本要素，如圖2所示。

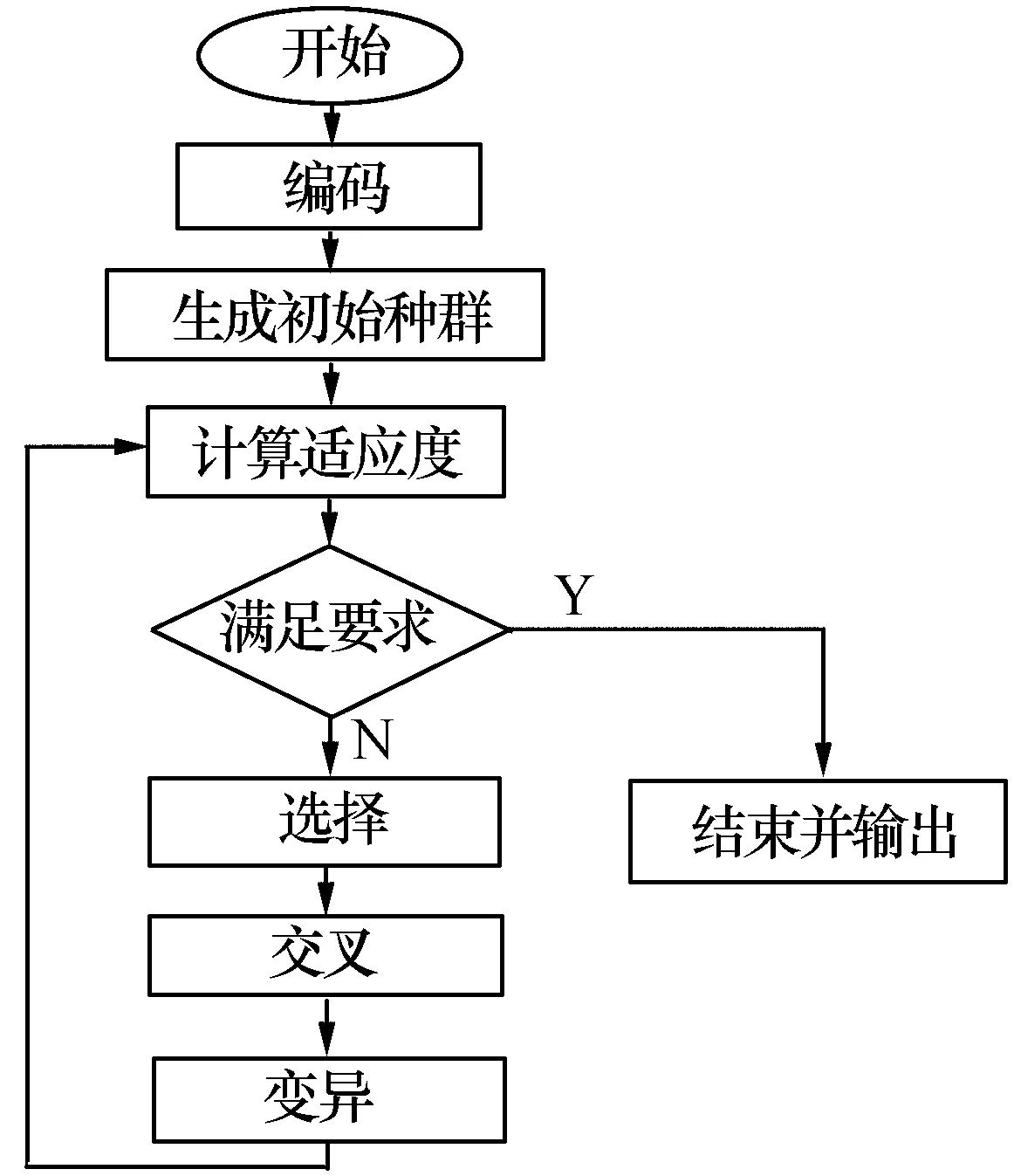
圖2　遺傳算法流程

1)編碼：通過編碼將各種解表示成遺傳空間可以直接進行算子操作的基因型串結構數據。方向圖綜合問題中包括每個陣元的電流幅度和相位兩個變量，通常采用級聯方式進行編碼。若N個陣元的天線陣列第k個天線單元激勵電流的幅度和相位分別為Ik和φk，采用級聯編碼后，每組數據結構可以表示成(I1,I2,…,IN, φ1,φ2,…,φN)的形式。

2)初始群體：為遺傳操作準備的由若干初始解組成的初始群體。

3)適應度函數：遺傳算法在搜索進化過程中用適應度函數值來評估個體或解的優劣，并作為以后遺傳操作的依據，通常取函數最大值或者最小值。

方向圖賦形綜合是一個多目標多參數的非線性優化問題，除了在賦形區需要逼近目標方向圖外，在非賦形區還要盡可能地抑制副瓣電平。因此，適應度函數要包括這兩個子目標函數。通常采用權系數法，把這兩個子目標函數按一定的權值相加，使之轉變成單目標優化問題。

設目標方向圖為F0(θ)，綜合后實際方向圖為F(θ)，允許的最大誤差電平為eth；目標最大副瓣電平為SLL0，實際最大副瓣電平為SLL；上述賦形主瓣與副瓣區域的目標函數可以分別表達成

(5)

(6)

對兩個子目標賦予不同的權重w1和w2，則適應度函數可以寫成

(7)

通過計算適應度函數的最小值，即可求得最優化方向圖。

4)遺傳操作設計，包括選擇、交叉和變異：

(1) 選擇：從群體中選擇優勝個體，把優化的解直接遺傳到下一代。個體適應度越高，其被選擇的機會就越多。

(2) 交叉：把兩個父代個體的部分結構互相交換重組，生成新的個體。

(3) 變異：對群體中的個體串的某些位置上的基因值作變動。

在實際方向圖綜合中發現，如果以陣元電流幅度和相位作為自由度，采用遺傳算法直接求解存在如下三個問題：

1) 自由度較多，每個陣元都包含幅度和相位兩個自由度，全陣列共有2N個自由度，隨著陣元的增加，計算量將急劇增加，收斂速度明顯變慢；

2) 需要同時兼顧賦形區域與副瓣區域兩個目標，很難選擇合適的權系數w1和w2來平衡這兩個優化目標，容易使某一種模式占優，導致另外一個優化目標難以實現，優化效果有限；

3) 初始值不確定，搜索范圍較大，容易陷入局部最優。

1.3優化零點算法

為了解決以上問題，結合Orchard綜合靈活直觀的優點，本文提出了基于Schelkunoff單位圓以及Orchard綜合的遺傳算法波束賦形，如圖3所示。由于陣元的電流幅相分布與方向圖零點位置存在對應關系，因此可以將求解電流幅相Ik，φk分布等價為求解零點位置θk，rk。通過詳細分析賦形區域和副瓣區域零點位置變化對方向圖的影響，還可以發現：

(1)賦形區域內零點位置的變化對副瓣區域電平的影響較小(第一副瓣零點除外)，因此，副瓣優化可以在各種優化算法前直接由解析方法計算完成；

(2)常見賦形如余割賦形等可以由僅僅移動賦形區域內零點徑向位置rR來實現，因此，自由度由Orchard綜合的N1+2N2個進一步減少為N2個。

基于上述特點，本文提出的優化零點算法流程分為兩個步驟：求解初值和賦形優化。首先，根據副瓣電平，通過解析法求得所有零點位置，將前述零點位置作為初始值；然后，將賦形區域零點徑向位置rk作為變量，通過遺傳算法求得最優解下的零點位置；最后，根據式(4)展開求得陣元幅相分布。

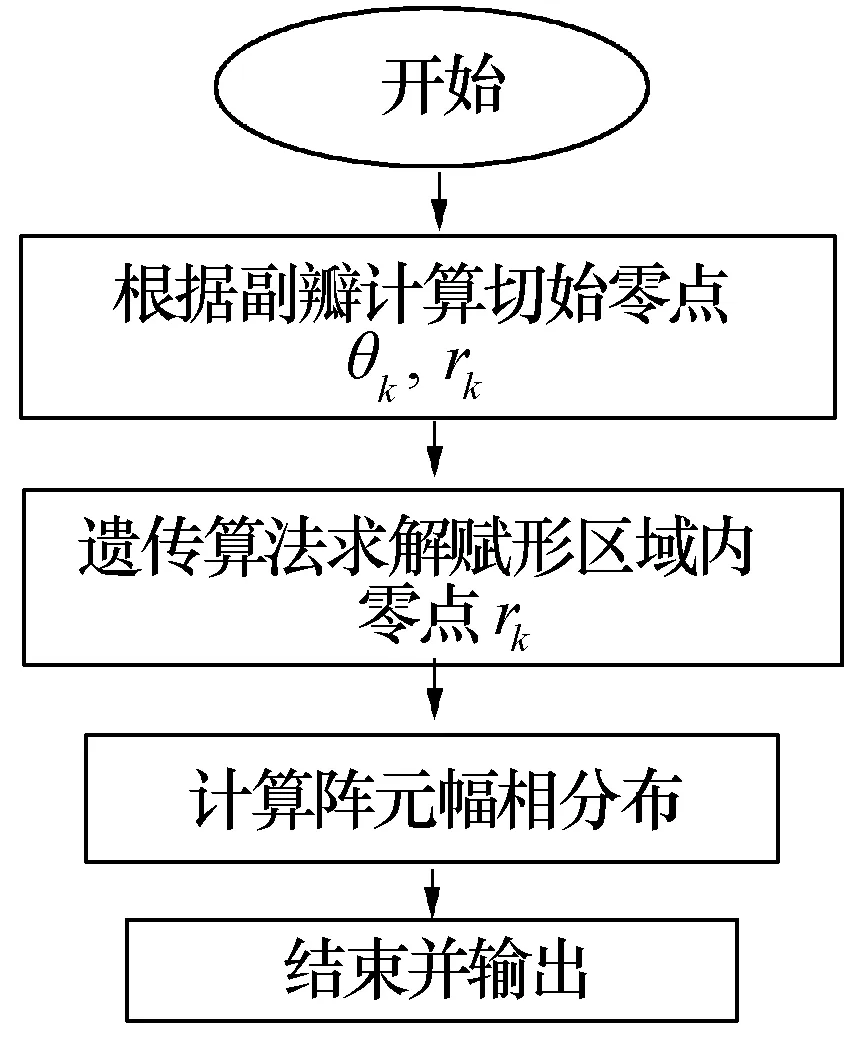
圖3　優化算法流程

相比于直接求陣元幅相分布的算法，本方法有如下兩個優勢：

1)副瓣約束已經由初始值通過解析法確定，適應度函數簡化為賦形區域的單目標函數，避免了多目標下權重的難以分配和單目標占優的問題；

2)對零點的移動方向加以限制，僅僅允許賦形區域內的零點沿徑向移動，算法自由度大幅減少，計算速度加快。同時，避免了二維空間搜索易陷入局部最優的問題。

2　計算實例

2.1程序實現

為了進一步減少與期望值之間的誤差，提高計算效率，本文還改進了一種界面化操作方案，可以自由移動零點位置，并實時顯示對應的方向圖。程序采用MATLAB的GUI工具編寫，界面同時顯示零點位置、對應方向圖、幅相分布以及賦形各項參數設置，如圖4所示。通過直接選中并移動賦形區域內的零點位置，將方向圖盡可能逼近期望值曲線。將此時的零點位置作為計算初始值，賦形區域內零點的rk作為自由度進行優化計算，進一步縮小搜索范圍，提高算法的收斂速度。應用遺傳算法，可以快速求得最優化的賦形。遺傳算法主要采用了MATLAB自帶優化算法工具箱中的GA函數來實現。

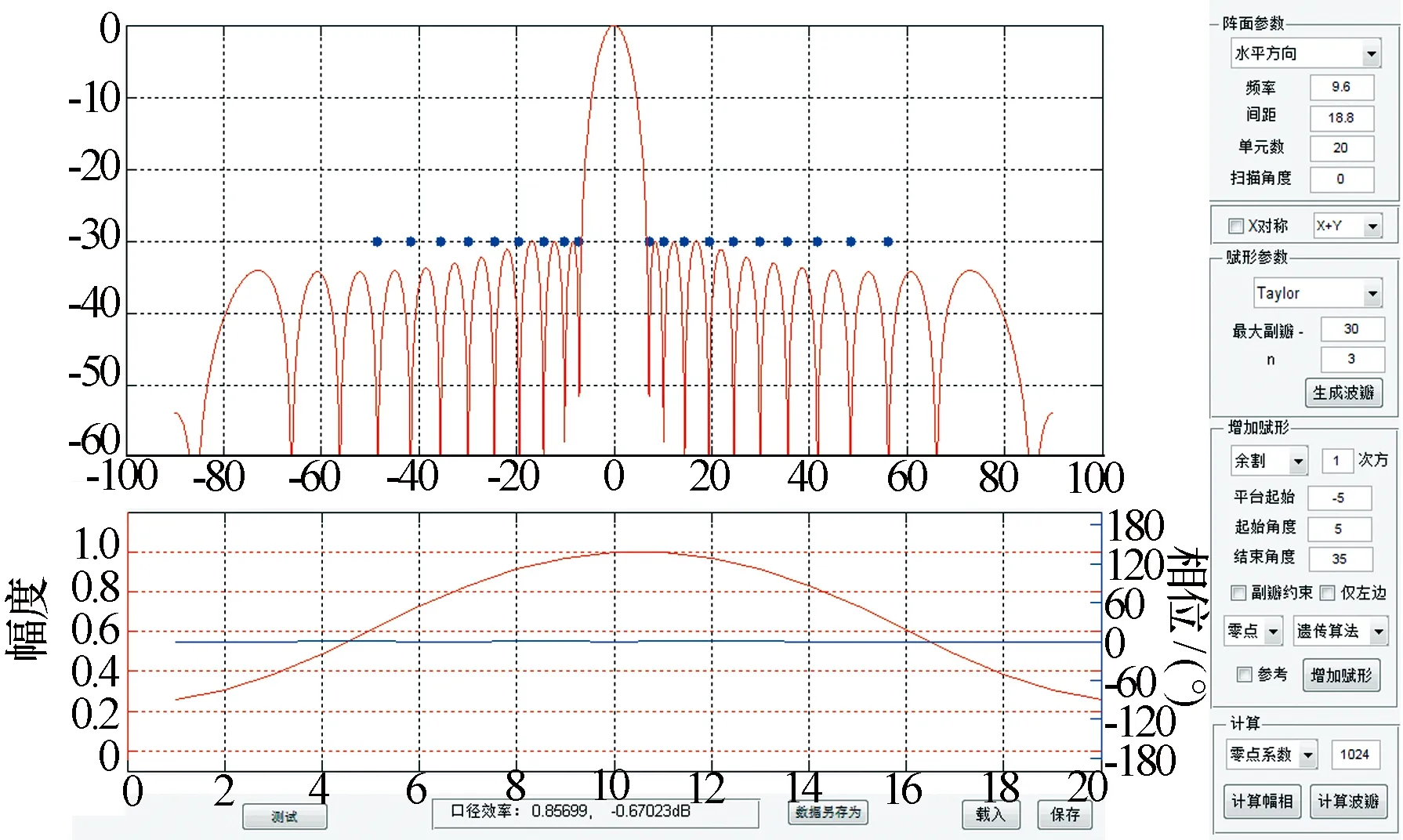
圖4　程序界面

2.2算法實例

2.2.1余割賦形

20個等間距排布的線陣，單元間距0.5個波長。優化每個陣元的幅度和相位，使陣列的主瓣方向滿足余割平方賦形，其余空間區域副瓣電平SLL小于-25dB。目標函數可以寫為

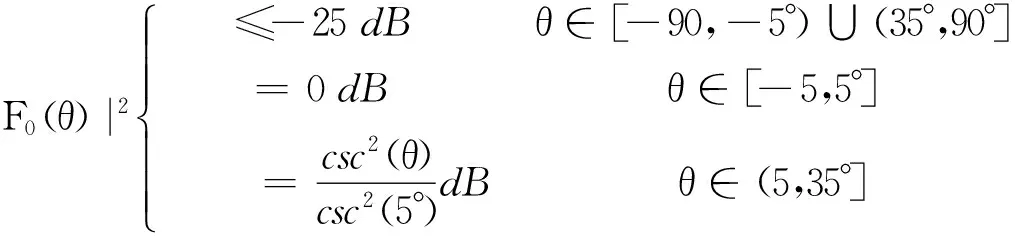
(8)

根據本文優化算法，首先計算副瓣區域零點分布。根據副瓣目標，不妨令線陣滿足SLL=-25dBTaylor分布，方向圖零點位置滿足解析表達式

(9)

以上述解析求得的零點位置作為初值，通過遺傳算法優化賦形區域內的五個零點徑向位置rk，以賦形區域內與期望值的誤差均值作為遺傳算法的適應度函數，此時，目標函數為單目標函數

(10)

經過300次迭代計算，優化后的方向圖以及幅相分布如圖5所示。作為對比，該賦形算例還采用了直接以每個陣元的Ik和φk作為自由度的遺傳算法，適應度函數采用加權系數法，如式(7)所示。同樣經300次計算后的方向圖和幅相分布如圖5、圖6所示。從圖中可以看出，采用本文方法優化后的方向圖不僅在賦形區域與期望值誤差非常小，而且副瓣完全滿足甚至優于設計要求。而采用直接幅相優化由于需要同時兼顧賦形區域和副瓣電平，優化效果十分有限。

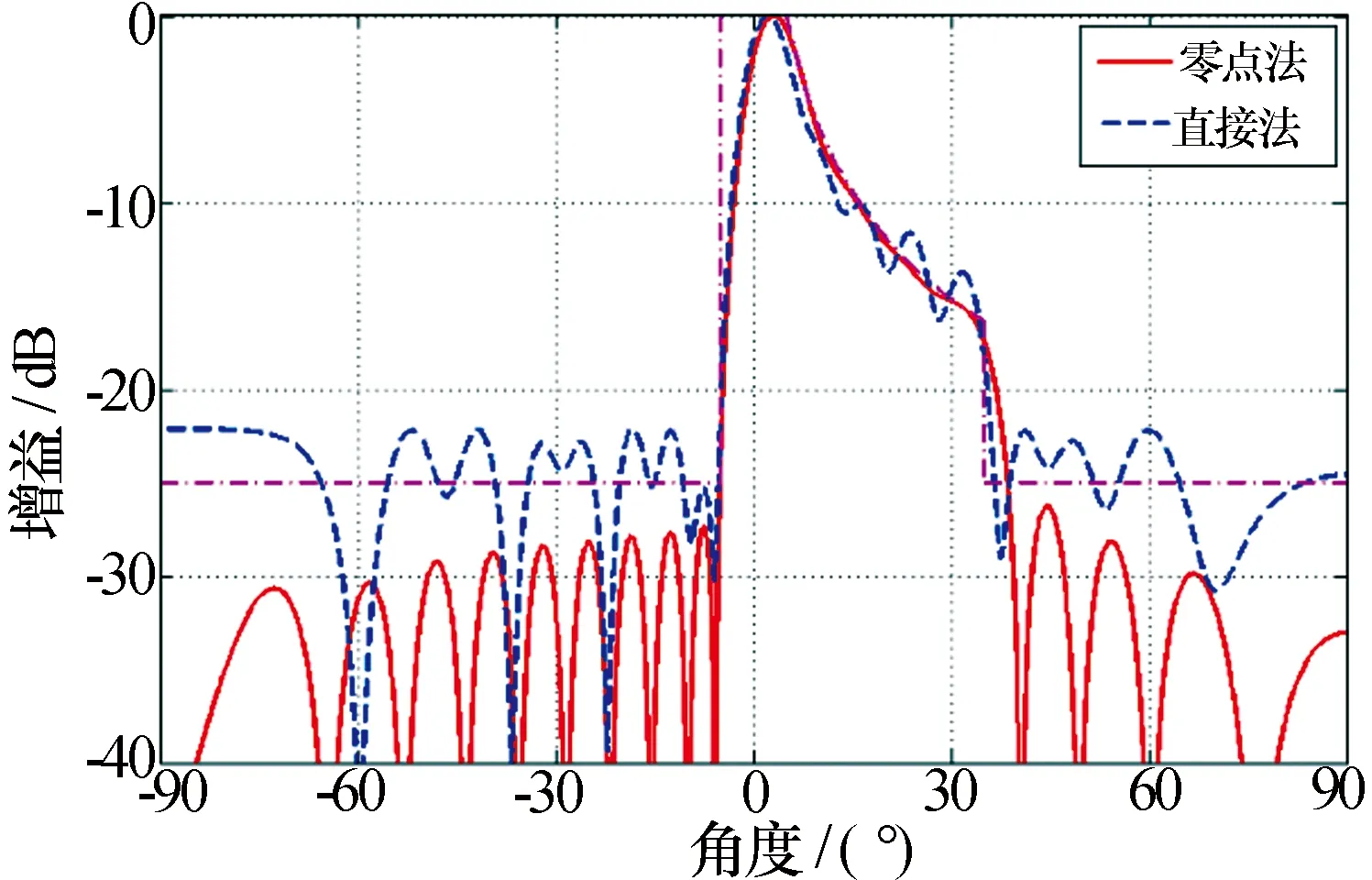
圖5　優化零點算法與直接幅相算法方向圖

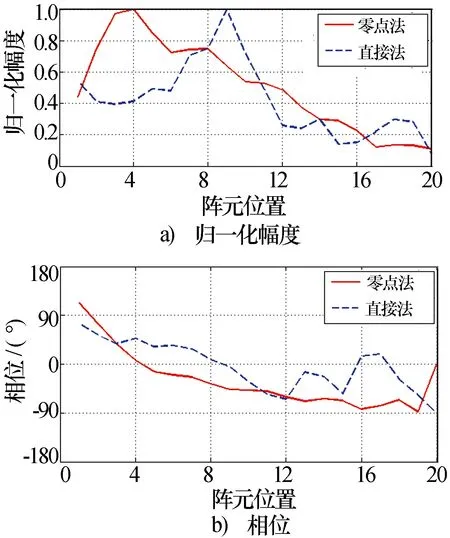
圖6　兩種算法每個陣元激勵幅相分布比較

2.2.2扇形波束

同樣為20個等間距排布的線陣，單元間距0.5個波長。目標函數(見圖7中點劃線)可以寫為

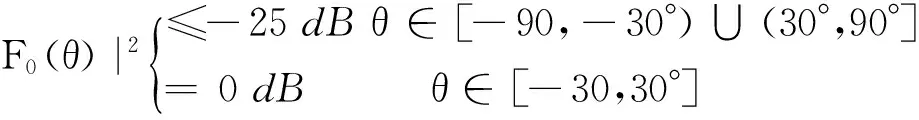
(11)

同樣采用算例1中的直接幅相遺傳算法和本文所述優化零點算法分別進行計算，方向圖和陣元的幅相分布如圖7和圖8所示。從圖7中可以看出，采用優化零點算法中賦形區域內的幅度起伏小于0.5dB，賦形區域外的副瓣小于-30dB，波束特性明顯優于直接幅相遺傳算法。

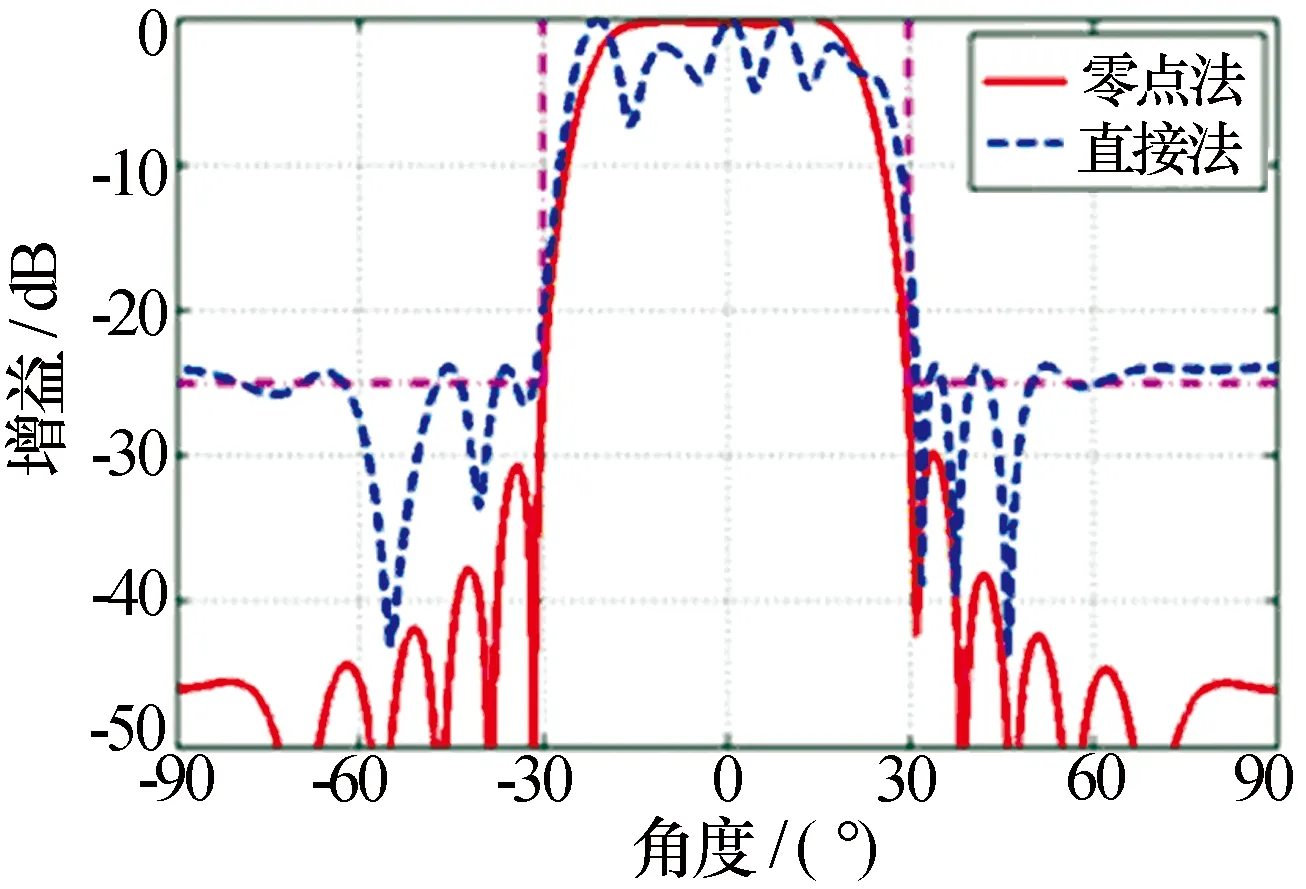
圖7　優化零點算法與直接幅相算法方向圖

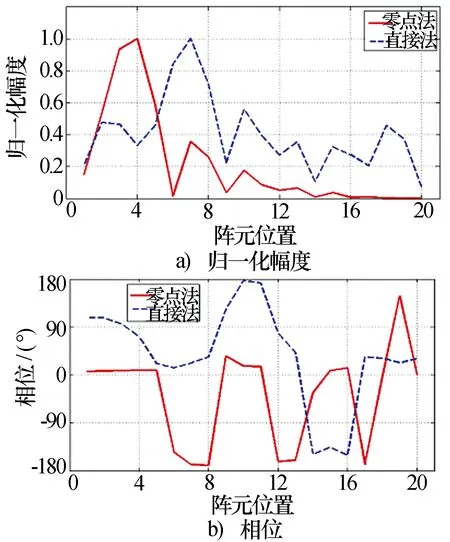
圖8　兩種算法每個陣元激勵幅相分布比較

需要說明的是，由于方向圖采用dB單位表示，而采用單位1表示時，實際的副瓣電平非常小，在0附近波動，當副瓣要求<-25dB以下時，陣元幅相的微小擾動都會對副瓣造成較大起伏，這也是采用直接計算幅相的遺傳算法時副瓣很難進一步降低的原因之一。同時，多目標優化也容易導致單目標占優。圖9為零點法和直接法的收斂速度比較，由于兩種算法的適應度函數不一致，將二者的最終收斂值進行歸一化后在圖9中顯示。從圖中可以看出，優化零點算法的收斂速度相比直接算法有了顯著提高。

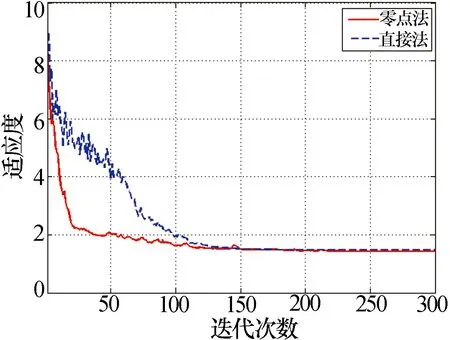
圖9　兩種算法收斂速度比較

3　結束語

本文提出了一種基于Schelkunoff單位圓以及Orchard綜合的優化零點算法，先通過解析方法計算零點位置，滿足副瓣約束，將求得的零點位置作為初始值，賦形區域內的零點徑向位置變化作為自由度，進行區域內單目標遺傳算法尋優。不僅避免了直接幅相計算中多目標均衡問題，也顯著減少了自由度，加快收斂速度。通過低副瓣平方余割波束和扇形波束兩個實例可以看出，副瓣區域和賦形區域均得到了優化，明顯優于直接幅相計算法所得的結果，說明這種算法具有很好的應用價值。

[1]MAILLOUXRJ.Phasearrayantennahandbook[M]. 2nded.Beijing：PublishingHouseofElectronicsIndustry, 2007.

[2]MARTINSCL,PATENUDEY,SEGUING.Lineararraybeamshapingusingfletcher-powelloptimization[C]//Antennas&PropagationSocietyInternationalSymposium.Philadelphia,PA:IEEEPress, 1986: 395-398.

[3]劉昊, 鄭明, 樊德森, 等. 遺傳算法在陣列天線賦形波束綜合中的應用[J]. 電波科學學報, 2002,17(5): 539-542.

LIUHao,ZHENGMing,FANDesen,etal.Synthesisofantennaarraysshaped-beamusinggeneticalgorithm[J].ChineseJournalofRadioScience, 2002, 17(5): 539-542.

[4]楊麗娜, 丁君, 郭陳江,等. 基于遺傳算法的陣列天線方向圖綜合技術[J]. 微波學報, 2005, 21(2): 38-41.

YANGLina,DINGJun,GUOChenjiang,etal.Patternsynthesisofantennaarrayusinggeneticalgorithm[J].JournalofMicrowaves, 2005, 21(2): 38-41.

[5]劉燕, 郭陳江, 丁君, 等. 基于粒子群算法的陣列天線波束賦形[J]. 電子測量技術, 2007, 30(6): 43-45.

LIUYan,GUOChenjiang,DINGJun,etal.PatternsynthesisofarrayantennabasedonPSO[J].ElectronicMeasurementTechnology, 2007, 30(6): 43-45.

[6]李緒平, 趙交成, 段霞霞, 等. 一種綜合賦形波束天線陣的組合算法[J]. 微波學報, 2007, 23(6): 26-28.LIXuping,ZHAOJiaocheng,DUANXiaxia,etal.Synthesisoftheshaped-beamarrayantennasusinganewcombinedalgorithm[J].JournalofMicrowaves, 2007,23(6): 26-28.

[7]楊永建, 王晟達, 馬健, 等. 基于改進粒子群算法的共形陣列天線綜合[J]. 現代雷達, 2012, 34(12): 64-67.

YANGYongjian,WANGShengda,MAJian,etal.Conformalantennaarraybeampatternsynthesisbasedonimprovedparticleswarmoptimization[J].ModernRadar, 2012, 34(12): 64-67.

[8]ORCHARDHJ,ELLIOTRS,STERNGJ.Optimizingthesynthesisofshapedantennapatterns[J].MicrowaveAntennas&PropagationIEEEProceedingsH, 1985, 132(1): 63-68.

王力男，1986年生，工程師。研究方為相控陣天線技術等。

何丙發男，1963年生，研究員級高級工程師。 研究方向為相控陣天線技術、通信天線技術等。

孫慶鋒男，1978年生，高級工程師。研究方為相控陣天線技術、毫米波天線技術等。

Synthesis of the Shaped-beam Array Antennas Using a Fast Algorithm

WANG Li，HE Bingfa，SUN Qingfeng

(Nanjing Research Institute of Electronics Technology,Nanjing 210039, China)

Afastalgorithmforsynthesisoftheshaped-beamarrayantennasispresented.ThisalgorithmisrealizedbymovingthezeropointpositionsontheSchelkunoff'sunitcircleusinggeneticalgorithm,basedontheOrchardsynthesis.Theprocedureisdividedintotwosteps: 1)analyticallycalculatetheoriginalzeropointpositionsaccordingtothesidelobelevel; 2)thefreedomofzeropointmovementintheshapingareaisrestrictedintheradicaldirection,andfindthebestresultwithsingle-targetbygeneticalgorithm.Comparedtothenormalantennashapingusingamplitude-phasecodinginthegeneticalgorithm,thismethodcanavoidthemulti-objectivetrade-offbetweenthesidelobelevelandbeamshapingaccuracyefficiently,andthefreedomofvariableforthealgorithmisreduced,theconvergencevelocityisalsoenhanceddramatically.Besides,lowsidelobelevelandbeamshapingwithhighprecisioncanberealizedsimultaneously.Theefficiencyforthisalgorithmisverifiedbyshapedsquare-cosecandfanbeamsample,anditcanfindwideapplicationsintheareaoffastbeamshapingforthearrayantennas.

shaped-beam；Orchardsynthesis；geneticalgorithm

10.16592/j.cnki.1004-7859.2016.08.016

王力Email：wangli860420@163.com

2016-04-26

2016-07-02

TN821+.8

A

1004-7859(2016)08-0070-05