“認識方程”教學實錄及思考

殷智強

“認識方程”教學實錄及思考

殷智強

課前思考

方程與不等式是刻畫數量關系的重要數學模型。“認識方程”的教學應將重心放在體驗方程模型的建立，體會方程思想上，教學難點則是如何引導學生學會順向思考，會用方程表示事物之間的數量關系。

通過前面四年的數學學習，學生已經積累了用算術方法解決問題的經驗，能夠運用算術方法快速地找到問題的答案。在這一過程中，學生運用的是以問題為導向的逆向思維。所以在列方程的過程中，由于受算術解題方法經驗的影響，學生習慣于把未知數作為目標，然后列式計算。而方程本質上是闡述一個事實，不以解決問題為目標，表達的是題目中最基本的等量關系，體現的是一種順向思維。逆向思維和順向思維體現了解決問題的兩種不同思考方向。在小學階段，由于解決的問題尚不復雜，許多問題其實都可以通過逆向思考的方式予以解決。而初中、高中階段的題目則需要通過順向思考列出方程，最后通過解方程得以解決。所以“認識方程”的教學目標不能停留在方程的概念性描述上，而應讓學生學會順向思維，獲得解決問題的另一種方法。因此在教學時，教師要通過巧妙的教學設計，逐步向學生滲透順向思考的方式，讓順向思考列方程成為一種習慣。

教學過程

一、導入

師：仔細觀察下面這些圖片，它們都有一個什么共同點？

生：這些標志當中都用到了天平。

師：天平有什么特點？

圖1　

生1：如果天平兩邊的質量相等，天平就會保持平衡；如果天平兩邊的質量不相等，天平就會傾斜，天平重的一端就會沉下去，輕的一端就會翹起來。

師：是的，這里就是利用天平的特點來象征公平與正義。在數學學習中，我們也會利用天平的特點解決一些問題。老師這里就有一臺天平。（課件呈現天平并進行介紹）

二、新授

1.根據數量關系列算式

師：（出示圖2）你看到了什么？

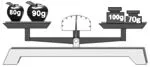
圖2　

生2：天平的左邊放了兩個蘋果，一個重80克，一個重90克；天平右邊有兩個砝碼，一個重100克，一個重70克，天平保持平衡。

師：你是怎么看出天平保持平衡的？

生2：天平的指針指向正中間。

師：那你能用一個算式表示出它們的數量關系嗎？生2：80+90=100+70。

師：（出示圖3）你又看到了什么？

圖3　

生3：天平的左邊放了一個重80克的蘋果和一塊積木，天平的右邊放了一個重100克的砝碼，天平向左邊傾斜。

師：天平向左傾斜說明了什么？你能像剛才一樣用一個算式表示出它們之間的數量關系嗎？

生3：80+一塊積木＞100。

生4：這樣寫太麻煩了，我們可以將這塊積木的質量假設為x克，用算式表示為80+x＞100。

師：太棒了，你居然想到了用字母表示這塊積木的質量。但是一定要將這塊積木的質量假設為x克嗎？設為其他字母可以嗎？（可以）只是我們通常將其設為x克。要使天平保持平衡，我們該怎么調整砝碼？

生5：可以在天平的右邊繼續放砝碼。

師：那好，在天平的右邊增加一個重100克的砝碼，看看天平兩邊又會發生什么樣的變化（如圖4所示）。

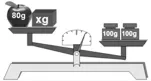
圖4　

生6：右邊的重一些。

師：那你能夠根據這幅圖列出一個算式嗎？生6：80+x＜200。

師：這時的天平還是不平衡，我們該怎樣調整砝碼呢？你是怎樣想的？

生7：說明天平左邊物體的總質量在100克和200克之間，增加的這個100克的砝碼太重了，可以換小一點的試試。

師：那好，我們將這個100克的砝碼換成一個50克的砝碼，看看結果怎么樣（如圖5所示）。（天平平衡了）你能根據這幅圖再列出一個算式嗎？

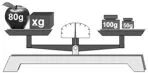
圖5　

生8：80+x=150。

師：老師這里買了一個重150克的蘋果，如果將其放在天平的左邊，閉上眼睛想一想，天平兩邊會發生怎樣的變化？能列出一個式子嗎？

生9：天平左邊會沉下去，因為150＞100+30。

師：我很好奇，如果將這個蘋果咬掉一口后放到天平的左邊會怎么樣？

圖6　

生10：天平還是向左邊傾斜。

生11：不一定，要看咬掉的這一口有多重。如果剛好是20克，天平會保持平衡；如果重于20克，天平會向右邊傾斜；如果小于20克，天平會繼續向左邊傾斜。

師：同意嗎？說得真好。那你能用式子表示出來嗎？

生11：150-x＜130，150-x=130，150-x＞130。

2.對式子進行分類整理

師：同學們，通過剛才的學習我們列出了8個算式。你能將它們按照一定的標準分成兩類嗎？說說你的想法。

①80+90=100+70②80+x＞100

③80+x＜200④80+x=150

⑤150＞130⑥150-x＜130

⑦150-x=130⑧150-x＞130

生：可以按是否為等式分類；按是否含有字母分類。

師：大家在分類時用到了兩個標準：是否為等式和是否含有字母。請仔細觀察兩個特別的算式④和⑦。你知道為什么說它們特別嗎？

生12：因為它們既是等式又含有字母。

師：對，像這樣含有未知數的等式，在數學里我們稱為方程。這節課我們認識了數學王國里的一位新成員——方程。（板書課題：認識方程）你能告訴大家方程具有什么特點嗎？

生13：方程有兩個特點，一是必須含有字母，二是必須為等式。

師：了不起。請你繼續完成下列練習題（課件出示圖7）。

“全人”是指全面發展的人、具有主體性且能夠把握自己命運的人。因此，“全人教育”強調人的整體發展，尊重個體的多樣性，其目的就是培養有道德、有知識、有紀律、有能力，和諧發展的“完人”[7]。現階段，我們所有的教育工作者其重要使命是要培養“通德、通識、心智和諧”的人，大學英語教師最直接的方法就是在課程教學設計中彰顯和體現此觀念及其理論。不難發現本次設計中的幾處全人教育理念：女性地位提高、女性自我意識覺醒、客觀公正地評價反饋等，特別是寫作作業，同學會用真實的經歷和情感描寫自己的母親，對于內斂保守的中國人來講，這是多么好的一次機會！

圖7　

生14：1號肯定是方程，既含有未知數又是等式。

生15：2號可能是方程，也可能不是方程。因為只知道它是一個等式，不知道墨水后面是不是未知數。

3.鞏固練習

師：請根據圖8提供的信息分別列出方程。

圖8　

生16：x+90=120。

生17：x+x+x+x=190，或者4x=190。

師：剛才我給了大家天平，讓大家根據相關信息列出方程。現在沒有天平，大家還能列出方程嗎？（出示題目：3包相同的餅干，總質量是210克，每包餅干的質量是多少克？）

生18：3x=210。

生18：x表示一包餅干的質量，3x就表示3包餅干的質量，題目中已經告訴我們3包餅干的總質量是210，所以方程是3x=210。

師：那也就是說我們先找到未知量，并將其假設為x，然后想辦法找到題目中的等量關系列方程。那再來一道題：一個長方形的長為13厘米，周長為40厘米，長方形的寬為多少厘米？

生19：長方形的周長計算公式是（長+寬）×2，假設長方形的寬為x厘米，這道題可列方程為（13+x）×2=40。

師：你是利用長方形周長的計算公式列方程。那方程究竟有什么好處呢？（出示例題：王老師帶100元到文具店為學生購買獎品。筆記本每本6元，她購買了4本，還買了8支鋼筆，售貨員找回10元，你知道王老師買的鋼筆單價是多少嗎？）你能用方程表示出題中的數量關系嗎？

生20：6×4+8×x=100-10。

師（故作疑惑狀）：這個方程這么長，誰能幫我翻譯一下，讓大家都明白？

生21：筆記本每本6元，買了4本，6×4表示買筆記本花的錢；將鋼筆的單價假設為x元，買了8支，8×x表示買鋼筆花的錢；6×4+8×x表示所花出去的總錢數；100-10表示的也是所花出去的總錢數，所以相等。

師：現在我終于明白了，一段看起來很長很復雜的文字，用方程表示出來更簡潔明了。

（作者單位：長沙市芙蓉區育才學校）

點評

從算術向代數過渡，是學生數學學習的重要轉變，也是重要的進步。代數研究的對象不僅包括數，還包括符號。處理符號是代數的本質特征。在代數里，用字母或其他符號表示數、表示性質、表示關系、表示運算等，就把數與數的關系推廣到了一般。

學生在算術學習過程中形成了一些基本的觀念。這些觀念中，有的與代數思維是相悖的。比如對運算的理解。在算術里，2+3表示的是一個運算過程，即把2和3加起來。在代數里，a+b不僅表示一個過程，還可以表示一個對象，即a與b的和。又如對等號（“=”）的理解。在算術里，學生傾向于把“=”理解為“宣布一種結果”。2+3=5，這里的“=”被認為是宣布2+3的結果。有這種認識的學生，難免會寫出這樣的錯誤式子2+3=5-1=4+6=10。而在代數里，“=”表示一種關系，等號兩邊是表示同一個東西。

方程的認識，關鍵是對這種關系的認識。這里的關系，當然是指數量關系。所謂數量關系，就是指數量之間的彼此依存與彼此約束。比如我有一些零錢，去商店買東西花掉了一些，還剩下一些。這里有三個數量，它們之間是有關系的。比如剩下的那些錢一定比原有的錢要少。這種關系就約束了這兩個量不可能隨意取值：在這里，原來10元，剩下8元，這是可能的；原來8元，剩下10元，通常就是不可能的。這種關系用不等式來刻畫。又如剩下的錢加上花掉的錢，一定等于原有的錢。這種關系也約束了這三個量不可能任意取值。這種關系用等式來刻畫。如果在一個等式里有未知數，我們就把這個等式叫做方程。因為這個等式反映了數量間的一種約束關系，其中的一個未知數不能任意取值。如果只有一個未知數的話，通常可以求出來。這就是解方程。

殷老師執教的“認識方程”一課，就是強調學生對數量關系的理解。天平的左邊放了兩個蘋果，一個重80克，一個重90克；天平的右邊有兩個砝碼，一個重100克，一個重70克，天平保持平衡。這4個蘋果的質量間滿足一種關系：80+90=100+70。這個等號不是通過計算、比較左右兩邊的結果得到的，而是通過觀察天平得到的。同樣，天平的左邊放一個重80克的蘋果和一塊積木，天平的右邊放一個重100克的砝碼，天平向左邊傾斜。這三個量之間又有一種關系，這種關系用不等式刻畫：80+x＞100，這里的大于號同樣不是通過計算、比較左右兩邊的值得到的（事實上，不等式左邊根本無法計算出一個具體結果來）。左邊放一個重150克的蘋果，右邊放100克和30克的砝碼各一個，天平偏左，用150＞100+30刻畫。現在，若把蘋果咬掉一口，再放回去，會如何？如此，讓學生不斷加深對數量關系的理解：在這里，刻畫數量關系的有不等式和等式。我們把目光集中到等式上來，如果等式里有未知數，就被稱為方程。這里的分類，不僅是對那些式子的分類，也是對式子背后的數量關系的分類。

不僅有有形的天平，還有無形的天平。長方形的長、寬和周長之間有可以用等式刻畫的數量關系，若其中有未知數，就是方程。王老師帶100元到文具店為學生購買獎品。筆記本每本6元，她購買了4本，還買了8支鋼筆，售貨員找回10元。這些數量之間也有可以用等式刻畫的關系，而鋼筆的價格未知，刻畫這些數量之間關系的等式就是方程。

在教學中，也可以適當引導學生關注數量關系對其中的數量的約束。比如天平的左邊放一個重80克的蘋果和一塊積木，天平的右邊放一個重100克的砝碼，天平向左邊傾斜。80+x＞100，這個不等式約束了積木的質量：30克是可能的，但10克是不可能的。不等式通常把其中的未知數約束在了某個范圍內。而對于只有一個未知數的方程，我們往往能確定其中的未知數。這個過程事實上就是用方程解決問題。

（長沙市教育科學研究院張新春）