加強思維訓練提升思維品質(zhì)
保春燕


摘要:數(shù)學教育的本質(zhì)就是發(fā)展學生的思維,數(shù)學教學中的思維訓練,是通過教師、學生、教材三者的多維互動,實現(xiàn)思維品質(zhì)的有效提升。在課堂教學中,教師要把思維訓練貫穿于數(shù)學課堂教學的各個環(huán)節(jié):創(chuàng)設(shè)情境,激發(fā)思維動機:主動探索,促進思維發(fā)展;總結(jié)深化,提升思維品質(zhì)。力求讓課堂成為思維訓練的力場,促使學生的數(shù)學思維在這一過程中獲得最大的發(fā)展!
關(guān)鍵詞:思維動機;思維的深刻性;靈活性;獨創(chuàng)性;思維品質(zhì)
加里寧說過“數(shù)學是思維的體操”。思維是事物的本質(zhì)屬性和內(nèi)部規(guī)律性在人腦中的反映,它是智力的核心。數(shù)學教育的本質(zhì)就是發(fā)展學生的思維。因此,在課堂教學中,教師要把思維訓練貫穿于數(shù)學課堂教學的各個方面,力求讓課堂成為思維訓練的力場。特級教師張齊華在《確定位置》一課的教學中給我們提供了具體的路徑。
一、創(chuàng)設(shè)情境,激發(fā)思維動機
動機是人們“因需要而產(chǎn)生的一種心理反應(yīng)”,它是人們行為活動的內(nèi)動力。因此,激發(fā)學生思維的動機,是培養(yǎng)學生思維力的關(guān)鍵因素。教師必須善于利用學生的好奇、好勝等心理特點,給學生創(chuàng)設(shè)學習數(shù)學的有效情境,從而為學生主動參與學習、積極進行思維提供最佳的心理準備。
課始,張老師以尋找最帥的兒子為切入點,在出示了一系列的照片后,學生嘩然,無法確定哪一個是張老師的兒子。接著,教者給出一組數(shù)對(4,2),學生們在激烈探討后,出現(xiàn)了不同的答案:有先從上到下,再從左至右數(shù)第4行第2列的;有先從上到下,再從右至左數(shù)第4行第2列的;有先從左至右,再從上到下數(shù)第4列第2行的;先從右至左,再從上到下數(shù)第4列第2行的。最終鎖定4個頭像,教者調(diào)侃:沒有這么多兒子,這里只有一個是我的。質(zhì)疑:到底哪一個是真的呢?問題出現(xiàn)在哪里?一語驚醒夢中人,生齊:老師,你沒說清楚?(4,2)中哪個指的是行,哪個指的是列?是從哪邊(即從什么方向)開始數(shù)的?
創(chuàng)設(shè)情境問題是思維的起點。有問題才會有思考,有思考才會有真正的思維活動。巧妙恰當?shù)靥岢鰡栴},創(chuàng)設(shè)良好的思維情境,能夠迅速集中學生注意力,激發(fā)學生的興趣和求知欲。張齊華老師的有效有意導入,使得學生們興趣盎然,快樂地踏上了思維之旅。
二、主動探索,促進思維發(fā)展
教學中,不僅要注意學生是否找出規(guī)律,更應(yīng)注意學生是否進行思考。創(chuàng)設(shè)情境后,放手讓學生用自己喜歡的學習方法進行學習,變教師的“教”為“導”、學生的“學”為“探”,從而引導學生自主探索合作交流,在此過程中培養(yǎng)學生獨立分析問題的能力,促進思維的發(fā)展。
1.溝通內(nèi)在聯(lián)系.培養(yǎng)思維的深刻性
思維的深刻性是指思維活動的抽象程度和邏輯水平,它集中表現(xiàn)在善于深入地思考問題,能從復雜的表面現(xiàn)象中,發(fā)現(xiàn)和抓住事物的規(guī)律和本質(zhì)。因此溝通知識間的內(nèi)在聯(lián)系,是培養(yǎng)思維深刻性的主要手段。
學起于思,思源于疑。朱熹說:“學貴有疑,小疑則小進,大疑則大進。”張老師對于學生的疑問,并沒有給出直接的答案。而是說:“我兒子最鐵的哥們的位置是(2,1)。”(在屏幕上圈出頭像)此時學生思緒萬千,想說的話特別多。張老師趁機讓學生進行小組討論,恰到好處。
學生們七嘴八舌地交流著自己的想法,張老師適時拋出:“現(xiàn)在你能找著我兒子了嗎?”生齊:“能!”
“哪一個?”
“第4列第2行。”
“帥嗎?”
“帥!”學生開心地大笑。
“說說你是怎么找著的?”
生1:那個最鐵的哥們的位置(2,1),就是左數(shù)第2列最下面第1行。所以,(4,2)就是第4列第2行。
“還有不同意見嗎?你們都同意他的說法嗎?”
生齊:“同意!” “恭喜你,答對了。”微笑示意其坐下。“今天我們一起來研究‘用數(shù)對確定位置’。”
接著給出幾個數(shù)對判斷位置。
在讓學生進行自主探索時,若遇到學生一籌莫展,不知從何下手的時候,張老師沒有通過直接的傳授,而是借助知識間的內(nèi)在聯(lián)系,以巧妙的疏導、殷勤的期待、熱情的鼓勵,引導學生深入思考,在思考中掌握知識,在掌握知識中發(fā)展自己的思維能力。
2.開拓思維空間.培養(yǎng)思維的靈活性
思維的靈活性指的是善于從不同角度和不同方面進行分析思考,學生思路開闊,能靈活變換某種因素,調(diào)整思路,從一個思路到另一個思路,從新角度去思考,善于巧妙地轉(zhuǎn)變思維方向,隨機應(yīng)變,產(chǎn)生適合時宜的辦法。
照片中的數(shù)對迎刃而解之后,張老師聯(lián)系實際:“你覺得你在教室里所處的位置,能用數(shù)對來表示嗎?”
生點頭大聲應(yīng)允:“可以。”
“第1列第1行在哪里?”(學生舉手示意)
有兩位學生同時舉手。(師皺眉)
啟發(fā)引導,師生明確:應(yīng)站在講臺的角度來看,第1列第1行的位置。
請出班長、副班長、體育委員,分別說出其所處的位置。
跟同桌說說自己所處的位置,并記住自己的位置,進行聽數(shù)對起立的游戲。
游戲步驟:
①師依次由慢漸快地報出:(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),聽到自己數(shù)對的學生一一起立,學生站成一列。
②請學生報數(shù)對,聽到自己數(shù)對的同學起立。(學生依照教者的形式報出數(shù)對)
(1,1),(2,1),(3,1),(4,1),(5,1),…,學生站成一行;
(1,1),(2,2),(3,3),(4,4),(5,5),…,學生站成一斜排;
(1,6),(2,5),(3,4),(4,3),(5,2),…,學生又站成另一斜排。
③師:都這樣說成一行一列,已沒什么新鮮感,下面誰來挑戰(zhàn):報一個數(shù)對就能站一列或一行或斜排?
生1報(2,0),沒人站。
生2報(1,1-7),師含笑:打包出售了。沒人理。
生3報(1,),師:這是數(shù)對嗎?眾生搖頭。
生4報(3,x),師相機板書。(3,1),(3,2),(3,3)…位置的學生,依次在其他學生提醒聲中緩緩起立。
師面對他們一一詢問:你是(3,x)嗎?第一位學生搖頭,師示意其坐下,繼而整列學生都被這一問題一一轟坐下。緊接著,師又面向他們一一再詢問:x可以代表1嗎?可以代表2嗎?……剛剛被轟坐下的學生又一一站起。整個課堂充溢著快樂的思辨,學生的思路逐漸開闊起來,從具體的數(shù)字到用字母來代替數(shù)字,這不正是學生思維靈活性的體現(xiàn)嗎?
3.提倡求異思維.培養(yǎng)思維的獨創(chuàng)性
思維的獨創(chuàng)性是指個體獨立思考創(chuàng)造出新穎的有社會價值的智力品質(zhì),是人類思維的高級形態(tài),是智力活動的獨立創(chuàng)造水平。學生的獨創(chuàng)性思維即善于探求新的途徑和尋找新的方法去解決問題,提出自己獨到的見解。在教學中要提倡求異思維,鼓勵學生探究求新,激發(fā)學生在頭腦中對已有知識進行“再加工”,以“調(diào)整、改組和充實”,創(chuàng)造性地尋找獨特簡潔的解法,培養(yǎng)思維的獨創(chuàng)性。
“一石激起千層浪”。用字母表示數(shù),把學生的思維又推向了另一個高起點。
張老師在拓展延伸環(huán)節(jié)中設(shè)置了這樣兩個問題:
①平面圖中位置出格了,怎么辦?
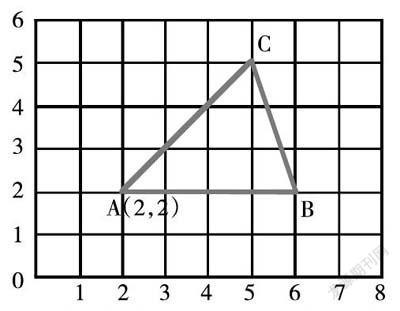
②給定三角形,你能用數(shù)對表示頂點的位置嗎?為什么不能?
利用變式訓練,一題多解或多題一解來開闊學生思路,引起思維變通,延伸思維。注重運用發(fā)散性思維方式提問,培養(yǎng)學生“立體思維”模式。徐利治教授曾指出:創(chuàng)造能力=知識量×發(fā)散思維能力。在這一訓練中,學生的創(chuàng)造性思維得以培養(yǎng)。
三、總結(jié)深化,提升思維品質(zhì)
學生的思維發(fā)展,應(yīng)指在事物的不同層次上向縱、橫兩個方面發(fā)展,向問題的深度和廣度發(fā)展,以達到對事物全面的認識的水平。為此,教師應(yīng)重視在數(shù)學教學過程中,當前問題趨于解決后,由此及彼,系統(tǒng)地研究相關(guān)的問題,揭示數(shù)學問題的實質(zhì),構(gòu)建數(shù)學思維模型,幫助學生提高思維的凝練能力。
張老師在小結(jié)提升環(huán)節(jié)引出:(1)確定一個點的位置,需要幾個數(shù)?(2)真的都需要兩個數(shù)嗎?這兩個問題將學生在確定位置時所要面臨的一維線性空間、二維的平面空間、三維的立體空間、多維的無限空間進行巧妙的溝通、聯(lián)系、梳理、鋪墊。我們教育者要用發(fā)展的眼光確定教學目標的生長點與發(fā)展點,用心唱好“我從哪里來,要到哪里去”,懂得從孩子一生的經(jīng)歷來教學,開拓學生的思路,總結(jié)深化,促進學生思維品質(zhì)的提升。
從張老師簡明扼要的總結(jié)中,我們深深領(lǐng)會到:數(shù)學確實是一門應(yīng)用性很強的學科,我們學習數(shù)學也是為了能夠更好地解決生活中的問題。通過實踐操作提升學生的思維品質(zhì),讓學生能夠看到數(shù)學的有趣、有用、真實的另一面。從而能夠做到使用數(shù)學知識解決問題,幫助學生迅速提升數(shù)學思維品質(zhì)。
學生的邏輯思維發(fā)展是一個長期的過程。因此,課堂教學應(yīng)以學生思維的發(fā)展為核心,將思維訓練貫穿于數(shù)學課堂教學的各個環(huán)節(jié),抓住學生思維的起始點、轉(zhuǎn)折點以及新的生長點、發(fā)展點,啟發(fā)引導,努力培養(yǎng)學生思維的深刻性、靈活性、獨創(chuàng)性;把時空有限的課堂變?yōu)椤叭巳藚⑴c、個個思考”的無限空間,這樣才能使絢麗的思維波瀾飛濺起更高的思維浪花……

