負梯度聲速下特征聲線與傳播時間快速求解方法

張維

?

負梯度聲速下特征聲線與傳播時間快速求解方法

張維

(中國船舶重工集團公司第710研究所，湖北宜昌443003)

求解特征聲線最直接的方法是采用“掃描-插值-迭代”的聲線跟蹤法，過程較復雜，計算速度較慢。將負梯度聲速環(huán)境下特征聲線的起始掠射角表示為聲速、海水深度、聲源與接收點相對位置的方程，通過采用量子粒子群算法求解方程直接獲得掠射角，進而確定特征聲線和傳播時間。與聲線跟蹤法相比，所提出的方法由于不存在數(shù)值累計誤差和角度插值誤差，因此精度更高，另外速度也更快，適合淺海負梯度環(huán)境下特征聲線與傳播時間的快速求解。

負梯度聲速；特征聲線；傳播時間；掠射角；量子粒子群

0 引言

淺海環(huán)境下，負梯度聲速是一種最典型的聲速剖面。在負梯度聲速環(huán)境下，特征聲線的起始掠射角可以表示為關于聲速、海水深度、聲源與接收點相對位置的較簡潔的方程。由于非線性的緣故，直接求解會有一定的困難，本文通過量子粒子群優(yōu)化算法求解方程從而進而確定特征聲線和傳播時間，簡化了計算，縮短了時間，提高了精度。這對于水下聲場的快速建模具有重要意義和工程應用價值。

1 特征聲線方程

在線性負梯度淺海模型中，根據(jù)聲線在聲源處是向海面還是向海底方向傳播，在接收點處是從海面還是海底方向接收以及聲線是否發(fā)生海面反轉(zhuǎn)三點不同，可將特征聲線分為圖1所示的8種類型。

(a)1=1??????(b)2=1

(c)1=0 ??????(d)2=0

(e)1=0 ??????(f)2=0

(g)1=1??????(h)2=1

圖1 特征聲線的8種類型

Fig.1 Eight styles of eigenrays

定義從海面到海底再到海面，或者從海底到海面再到海底這樣的過程為一個跨度。在圖1中和都表示聲線的跨度數(shù)，分別對應于聲線在海面反射或反轉(zhuǎn)的情況，在取值的過程中必須取整，以方便下面的計算。

其中，為聲線掠射角。則某一段聲線的水平距離和傳播時間可以分別表示為

(2)

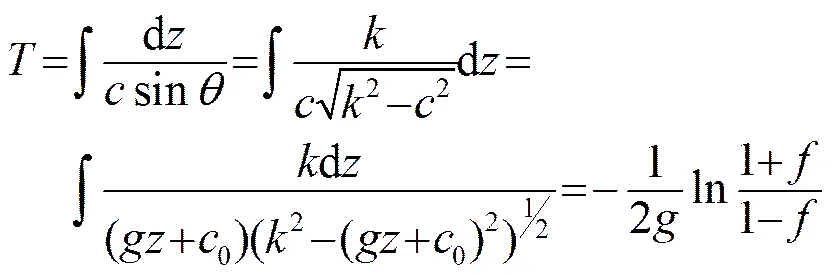
（3）對房地產(chǎn)投資活動的方法、地點或者性質(zhì)等進行改變。在投資開發(fā)決策階段，開發(fā)商會通過開展相關的可行性研究明確在某塊地上建設住宅的可行性、建設商業(yè)寫字樓的風險等，如果發(fā)現(xiàn)建設住宅的前景更好，那么在明確建設不同項目的風險大小之后，就可以直接從開發(fā)的性質(zhì)來有效避免建設商業(yè)寫字樓帶來的高風險。另外，開發(fā)商還可以在項目開展之前對相關的可行性進行專門的研究。

將式(2)應用到圖1中的8種不同特征聲線類型中，對于不同的特征聲線，可以得到以下幾種不同的特征聲線方程：

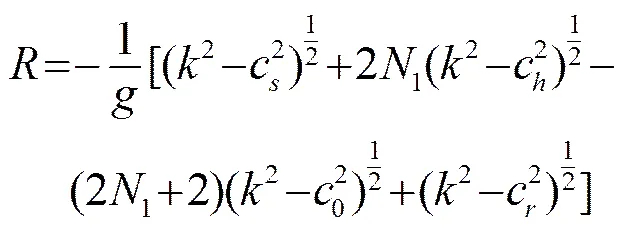
(5)

(6)

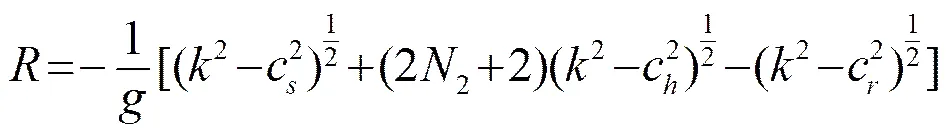
(8)

(9)

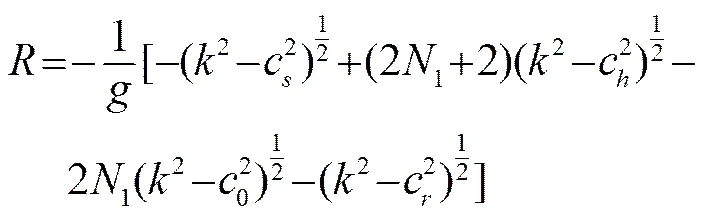
(11)

同理，式(3)對應的8種特征聲線也存在8種不同的表達形式，在此不再贅述。在水平距離、聲源深度、接收點深度以及聲速剖面已知的情況下，通過選取不同的跨度數(shù)求解以上方程得到中間變量，進而由式(4)~(11)求出聲源處聲線掠射角，即為特征聲線掠射角，然后通過由式(3)變形得到的8種表達式即可以獲得特征聲線傳播時間。

2 量子粒子群

式(4)~(11)是非線性方程，直接求解會有一定的困難，可以通過優(yōu)化算法快速求解。量子粒子群就是一種優(yōu)化算法，它利用波函數(shù)來描述粒子的狀態(tài)，通過解薛定諤方程得到粒子在空間中某一點出現(xiàn)的概率密度函數(shù)，最后由蒙特卡洛隨機模擬得到粒子的位置[8]

其中：和分別表示粒子和粒子的第維；表示代數(shù)；為(0, 1)之間的隨機數(shù)，時取負號，其余取正號；定義為所有粒子的局部最好位置的平均值：

(13)

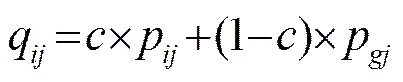
(15)

量子粒子群基本思想是在量子力學中，軌跡是沒有意義的。根據(jù)不確定性原理，粒子的位置和速度是不能同時確定的，粒子的量子行為，將使得粒子在整個可行解空間中進行搜索尋求最優(yōu)解。與其他優(yōu)化算法相比，量子粒子群具有以下優(yōu)點：(1) 量子粒子群具有較強的全局優(yōu)化能力；(2) 參數(shù)少，算法簡單，運行速度快，能較快地搜索到全局最優(yōu)值；(3) 實驗表明，量子粒子群具有良好的魯棒性。綜上所述，本文采用量子粒子群優(yōu)化算法快速求解非線性方程，量子粒子群算法簡單的流程圖如圖2所示。

3 仿真計算

解方程法與聲線跟蹤法求解結果對比如表1所示。聲線跟蹤法掃描時分別采用0.05°和0.5°作為俯仰角掃描間隔。采用0.5°的俯仰角掃描間隔時，由于間隔較大，漏掉了其中的兩條特征聲線。從時間上來講，解方程法比聲線跟蹤法要快很多，解方程法求解特征聲線和傳播時間共耗時0.2 s，采用0.05°和0.5°的俯仰角掃描間隔時，耗時分別為2.8 s和0.7 s。從精度上來講，解方程法非常接近理論值，與實際接收點深度相比最大僅相差0.005 m，采用0.05°和0.5°的俯仰角掃描間隔時，接收點深度最大相差分別為0.038 m和0.99 m，傳播時間精度分別在0.1 ms和毫秒量級，這主要是由于聲線跟蹤法的數(shù)值累計誤差和角度插值誤差所引起的。以上結果說明，采用聲線跟蹤法求解特征聲線和傳播時間的結果受掃描間隔的影響很大，掃描間隔越小精度越高，但耗時越長，相反，掃描間隔越大，耗時越短，精度越低，甚至有可能漏掉其中的某些特征聲線。解方程法則不存在以上這方面的問題，結果非常接近理論值，且速度很快，適合負梯度聲速信道的快速求解。

表1 兩種不同方法對特征聲線與傳播時間的求解結果比較

4 結論

本文根據(jù)淺水負梯度聲速信道的特點和聲線傳播規(guī)律，將發(fā)射掠射角表示為聲速、海水深度、聲源與接收點相對位置的方程，通過量子粒子群優(yōu)化算法求解非線性方程直接獲得掠射角，進而確定特征聲線和傳播時間。

與傳統(tǒng)的聲線跟蹤法相比，不存在漏掉某些特征聲線的現(xiàn)象，由于不存在數(shù)值累計誤差和角度插值誤差，因此精度很高，結果非常接近理論值，速度也很快，適合某些簡化條件下信道的快速求解。

[1] MERCER J A, FELTON W J, BOOKER J R. Three dimensional eigenrays through ocean mesoscale structure[J]. J Acoustic Soc Am, 1985, 78(1): 157-163.

[2] YANG Shie. Theory of underwater sound propagation[M]. Harbin: Harbin Engineering University Press, 2009: 74.

[3] 王百合, 馮西安, 黃建國. 一種分層海洋中求取本征聲線的新方法[J]. 微處理機, 2006, 27(1): 63-65.

WANG Baihe, FENG Xi’an, HUANG Jianguo. A new method for eigenrays searching in stratified ocean[J]. Microprocessors, 2006, 27(1): 63-65.

[4] 盛振新, 劉榮忠, 郭銳, 等. 分層海洋中求取本征聲線數(shù)值方法研究[J]. 微處理機, 2010, 31(5): 90-92.

SHENG Zhenxin, LIU Rongzhong, Guo Rui, et al. A modified method for eigenrays searching in stratified ocean[J]. Microprocessors, 2010, 31(5): 90-92.

[5] 王恕銓. 求解三維本征聲線的一種新方法[J]. 聲學學報, 1992, 17(2): 155-157.

WANG Shuquan. A new method of three-dimensional eigenray-tracing[J]. Acta Acustica, 1992, 17(2): 155-157.

[6] Tappert F D, Tang X. Ray chaos and eigenrays[J]. J Acoustic Soc Am, 1996, 99(1): 185-196.

[7] 張維, 楊士莪, 湯云峰, 等. 不平整海底環(huán)境下的淺海本征聲線求解方法[J]. 哈爾濱工程大學學報, 2011, 32(12): 1544-1548.

ZHANG Wei, YANG Shie, TANG Yunfeng, et al. A new method of seeking eigen rays in shallow water with irregular seabed[J]. Journal of Harbin Engineering University, 2011, 32(12): 1544-1548.

[8] 楊傳將, 劉清, 黃珍. 一種量子粒子群算法的改進方法[J]. 計算技術與自動化, 2009, 28(1): 100-103.

YANG Chuanjiang, LIU Qing, HUANG Zhen. One method of improving quantum-behaved particle swarm optimization[J]. Computing Technology and Automation, 2009, 28(1): 100-103.

An approach to rapidly acquiring eigenrays and transmission times in the environment of negative gradient sound speed

ZHANG Wei

(Yichang Research Institute of Testing Technology, Yichang 443003, Hubei,China)

Thedirectapproachto acquiring eigenrays is the method of ray tracing by “scanning-interpolation- iteration”. However, the procedure is complicated and the calculation speed is slow. When the gradient of sound speed is negative, the original grazing angle can be expressed as equations involving sound speed, seabed depth and the relative position between source and receiver. By solving the equations of the original grazing angle with QPS algorithm, the eigenrays and corresponding transmission time can be acquired conveniently. Compared with the method of ray tracing, because there are no accumulative error and angle interpolation error, the precision of the method introduced in this paper is higher. In addition, the calculated speed is so fast that the method is suitable for getting eigenrays and corresponding transmission times rapidly in the environment of negative gradient sound speed.

negative gradient sound speed; eigenray; transmission time; grazing angle; Quantum Particle Swarm(QPS)

P338

A

1000-3630(2016)-01-0020-04

10.16300/j.cnki.1000-3630.2016.01.005

2015-04-29;

2015-08-11

國家安全重大基礎研究項目(613110010202)

張維(1984－), 男, 湖北鐘祥人, 博士, 研究方向為海洋聲場分析。

張維, E-mail: zhangwei667@163.com