構建幾何模型求三角形面積的最大值
康峰
(山東省新泰市實驗中學)
構建幾何模型求三角形面積的最大值
康峰
(山東省新泰市實驗中學)
一、問題展示,導入課題
師:同學們,近幾年各地的中考題中經(jīng)常涉及一類求面積最大值的問題。
(課件展示幾個涉及求面積最大值的中考題)
師:同學們在解決這類題目時,往往遇到的困難是解題思路不清晰或者是解題方法復雜。通過這節(jié)課的學習,希望同學們能夠明確這類題目的解題思路,探究出解決問題的簡單方法。
(板書課題:構建幾何模型求三角形面積的最大值)
師:首先請同學們完成下面的一個基礎題目。
二、問題探究,構建模型
(課件展示一個基礎題目,讓學生自主完成)
已知:點A(0,2),B(4,0),C(3,3),求△ABC的面積。
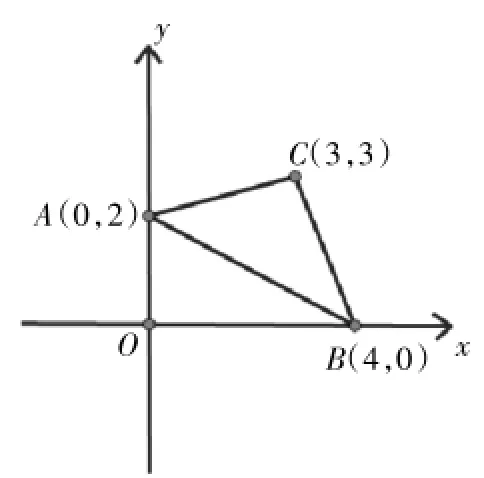
(教師巡視,發(fā)現(xiàn)學生通常采用兩種方法求解:一是過點C作CD⊥y軸于D,利用S△ABC=S梯形OBCD-S△ADC-S△ABO,一是過點C作CE⊥x軸于E,利用S△ABC=S梯形AOEC+S△CEB-S△ABO)
(讓學生相互交流作法)
師:找一位同學回答一下你的做法。
生1:過點C作CD⊥y軸于D,S△ABC=S梯形OBCD-S△ADC-S△ABO=5。
師:回答得非常好!還有沒有其他做法?哪位同學說一下?
生2:過點C作CE⊥x軸于E,S△ABC=S梯形AOEC+S△CEB-S△ABO=5。
師:很好,剛才兩位同學都是利用了“和差法”來求三角形ABC的面積。我們還能不能找到其他做法呢?
(展示課件)
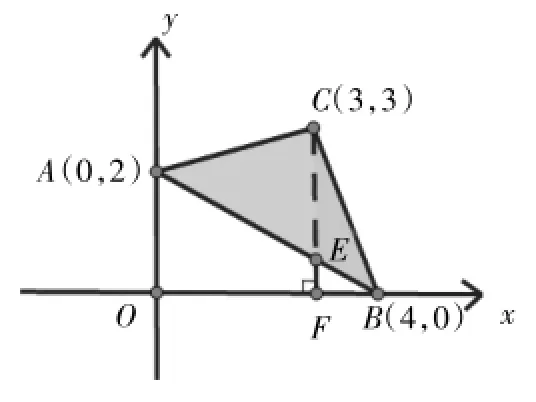
師:如果過點C作CF⊥x軸于F,交AB于點E,那么S△ABC= S△AEC+S△CEB.同學們想一想,△AEC與△CEB有什么關系?
生3:可以把CE看做它們共同的底。
師:很好,那么△ACE中CE邊上的高可以用誰來表示?△BCE中CE邊上的高可以用誰來表示?
生4:△ACE中CE邊上的高可以用OF表示,△BCE中CE邊上的高可以用BF來表示.
師:我們知道,解決數(shù)學問題時,用整體思想有時可以簡化一些解題步驟。在這里,我們可以把OF和FB相加作為一個整體來計算,這樣我們就可以得到求三角形ABC面積的一種新方法了。
師:同學們,你能用這種方法算出三角形ABC的面積嗎?試一試,交流一下你們的做法。
(教師巡視引導)
師:我找一名同學說一下是怎樣算出三角形ABC面積的?
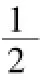
師:非常好!下面我們利用這種求三角形面積的方法來解決一類求面積最大值的問題。
三、應用模型,解決問題
(展示課件)
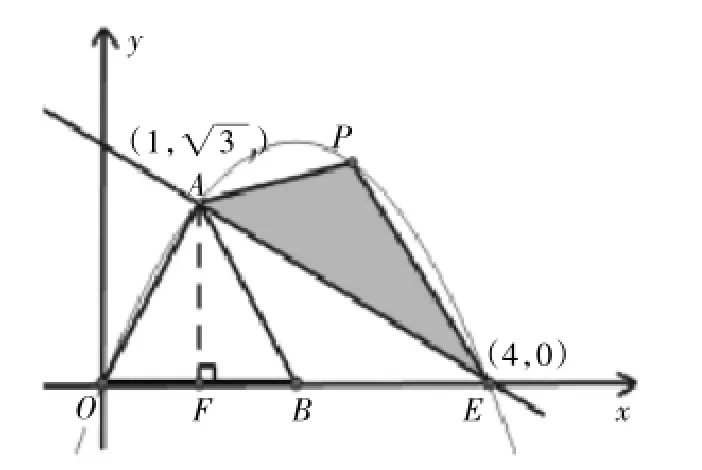
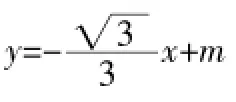
(1)求點E的坐標;
(2)求過A、O、E三點的拋物線的解析式;
(3)若點P是(2)中求出的拋物線AE段上一動點,設△APE的面積是S,求S的最大值.
師:請同學們先完成本題的前兩問。
(2分鐘后投影展示生6的答案)制約因素得到滿足時,該因素往往成為主導因素。從兩者的概念來說,主導因素和限制性因素都是相對于農(nóng)業(yè)生產(chǎn)所在的地區(qū)來說,而不是對于某種農(nóng)作物來說,例如,寧夏平原發(fā)展水稻種植的主導因素是水源,而不能說水稻種植業(yè)的主導因素是水源,寧夏平原地形平坦,沖積平原土壤肥沃,夏季光熱充足,但降水量少,所以其能發(fā)展水稻的主導因素是水源。如果要問寧夏大面積發(fā)展水稻種植的限制性因素是什么?這時應該回答是降水。
在確定主導因素和限制性因素時,除了考慮所在地區(qū)的特點外,也要綜合考慮所發(fā)展事物本身的特點。例如,珠江三角洲的基塘農(nóng)業(yè),是在特有的地形氣候條件下形成的,當?shù)氐貏莸屯荩潘粫常貏e是一下雨容易積水,當?shù)厝艘虻刂埔耍谀喑商粒涯酁榛愿脑飚數(shù)氐匦螢橥黄瓶冢纬闪嘶赁r(nóng)業(yè),低洼的地勢成為基塘農(nóng)業(yè)發(fā)展的突破口,因此地形是它的主導因素。但從另一方面來說,地形卻是發(fā)展其他農(nóng)業(yè)生產(chǎn)的限制性因素,如,珠江三角洲多水患的特點,排水不良,這就成為水稻生產(chǎn)的限制性因素。
因此,我們在做主導因素與限制性因素分析時,一定要分清所屬的地區(qū)特點和所面對的生產(chǎn)活動特點。分析那些因素是優(yōu)勢條件還是劣勢條件,一般優(yōu)勢條件就從主導因素方面去分析,劣勢條件從限制性因素方面去分析。所以說,讓學生掌握“主導因素”與“限制性因素”是學會區(qū)位評價的關鍵,建議我們的課本編寫者在教材中應該增加這兩個基本概念。
[1]趙志強.因素分析法在高中地理教學中的應用研究[D].東北師范大學,2008.
[2]商幸豐.淺議地理教學方法設計中的幾個問題[J].中學地理教學參考,1993.
·編輯張珍珍

