恒定溫度應力下的模擬IC加速退化試驗研究

吳兆希，李曉紅，鄧永芳，蔡建榮，楊少華

（1.中國電子科技集團公司第二十四研究所，重慶　400060；2.工業和信息化部電子第五研究所，廣東　廣州　510610）

?

恒定溫度應力下的模擬IC加速退化試驗研究

吳兆希1，李曉紅1，鄧永芳1，蔡建榮1，楊少華2

（1.中國電子科技集團公司第二十四研究所，重慶400060；2.工業和信息化部電子第五研究所，廣東廣州510610）

研究了在不同恒定溫度應力條件下某型號驅動器的模擬集成電路的加速退化試驗。首先，確定了該型驅動器的敏感參數，并建立了敏感參數的退化模型；然后，計算得到了器件在加速應力下的偽壽命；最后，利用阿倫尼斯模型對偽壽命數據進行分析，外推得到了器件的激活能及其在正常工作應力條件下的壽命信息。

加速退化試驗；阿倫尼斯模型；激活能；驅動器

0　引言

隨著現代電子系統綜合性和復雜性的不斷提高，系統的可靠性變得越來越重要了。半導體器件作為現代電子裝備的最重要的組成部分，其可靠性在很大程度上決定了整個電子裝備的可靠性。而半導體器件的可靠性根據其所處應力條件的不同可以分為兩類：貯存可靠性和工作可靠性。由于高可靠、長壽命的產品在正常的試驗條件下，能夠獲得的產品失效數據甚少，導致采用傳統的基于失效數據的可靠性分析變得相當困難。基于此，基于性能退化的可靠性分析便成為了一種評估高可靠產品的可靠性和壽命的有效方法［1］。為了能夠在較短的時間里觀察到產品的性能退化趨勢，需采用產品性能加速退化試驗來加速產品的退化。本文將對某型號驅動器的模擬集成電路在恒定溫度應力條件下的工作可靠性進行研究，進而推算其在正常工作應力條件下的壽命信息。

1　加速試驗的基本概念

加速試驗的基本原理是在不改變器件的失效機理的前提下，通過適當地提高誘發器件失效的應力條件 （溫度、濕度、電壓、電流和振動中的一種或幾種的組合）來加速器件的退化或失效。加速試驗可用來發現并識別半導體器件潛在的失效機理，并對這些失效機理在電子系統中發生的概率或速率進行評估［2］。

在利用加速試驗獲得半導體器件的可靠性信息（失效率、平均壽命等）后，即可利用引起半導體器件失效的加速模型來外推得到器件在正常應力條件下的失效率和壽命等可靠性信息［3］。

2　加速退化試驗方案設計

將該型號驅動器的樣品分為3組，每組均為30只樣品。其加速退化工作壽命試驗條件為：電應力按照產品詳細規范施加，溫度應力分別為100℃、125℃和150℃，試驗期間每1 000 h對電路可能的敏感參數進行監測，監測的參數共8個。由于在3個不同試驗溫度下電路參數的退化規律是一致的，現選取試驗溫度為125℃，經歷3 000 h加速退化試驗后的電路參數的變化情況來確定電路的敏感參數，監測的電路參數的變化情況如表1所示。

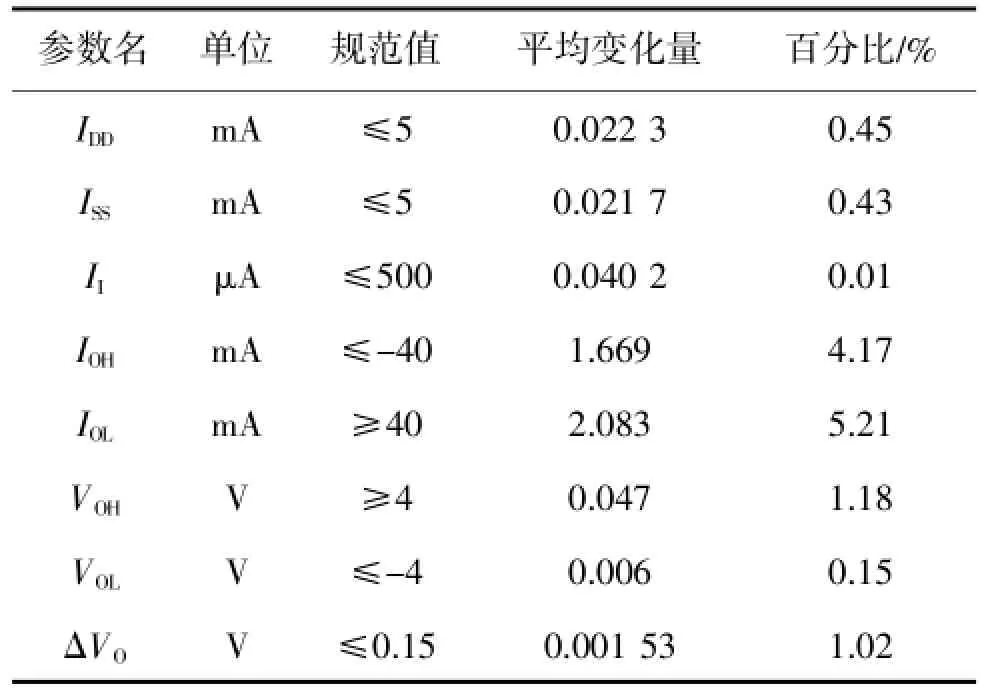
表1　監測的驅動器電參數變化情況

選擇試驗前后變化百分比最大的參數IOL作為敏感參數，對其數據進行分析。125℃的加速條件下IOL的變化情況如圖1所示。

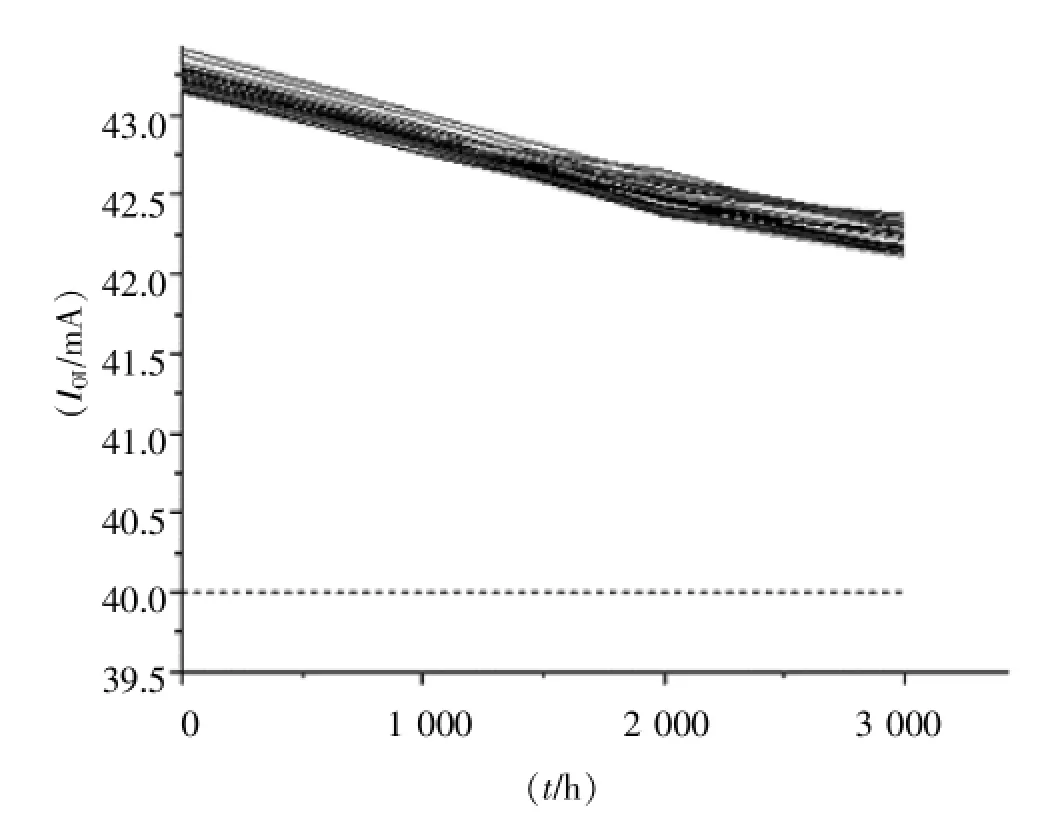
圖1　125℃溫度應力下IOL的變化情況

3　試驗數據分析

3.1試驗電路的偽壽命的計算

由圖1可以看出，IOL與試驗時間之間基本滿足線性關系，根據每只電路的線性擬合方程，可以推算出該試驗條件下IOL下降至40 mA的時間點，該時間點即為該試驗條件下電路的偽壽命。

假定線性退化方程為：

IOL=at+I0（1）

式 （1）中：a——常數；

t——試驗時間；

I0——t=0時，電流的初始值。

根據測試數據可以得到其線性擬合方程為：

IOL=-0.000 12 t+42.963 33（2）

擬合的相關度R2=0.928 57，將電路失效判據IOL=40 mA帶入上式，即可得到該電路的偽壽命t= 246 94.4 h。

同理可以得到其他試驗樣品的偽壽命，計算結果如表2所示。

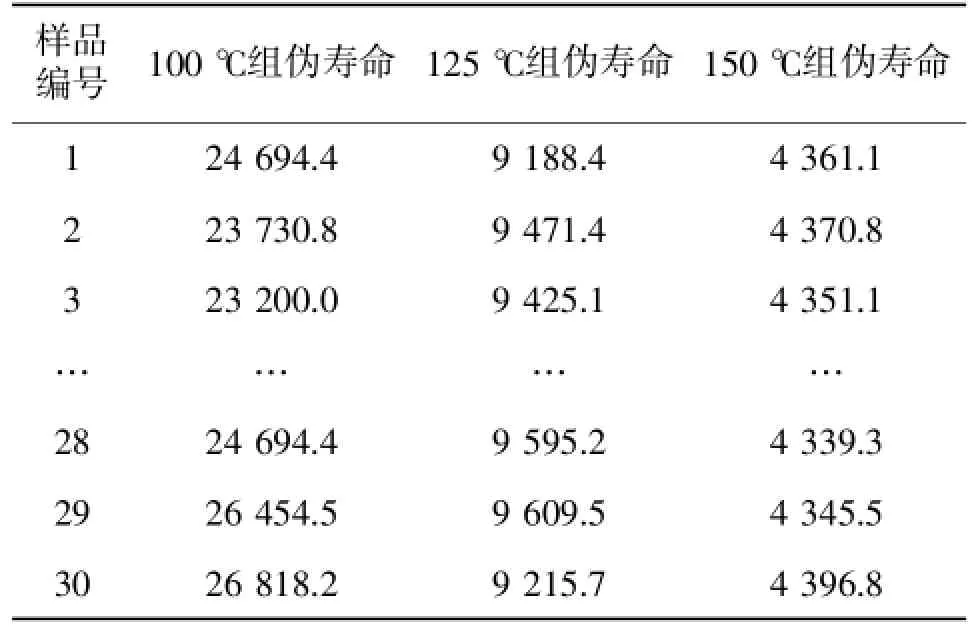
表2　不同溫度應力下的產品的偽壽命數據　t/h

3.2偽壽命數據分析擬合

將偽壽命數據繪制成直方圖，直方圖的分組數量可以由公式 （3）來確定［4］，即：

k=1+3.31g（n）（3）

式 （3）中：k——分組數；

n——樣品個數。

本文中每個溫度應力下樣品數n=30，將其帶入 （3）式，將結果取整后可得k=6。

以125℃組為例，繪制的偽壽命直方圖如圖2所示。

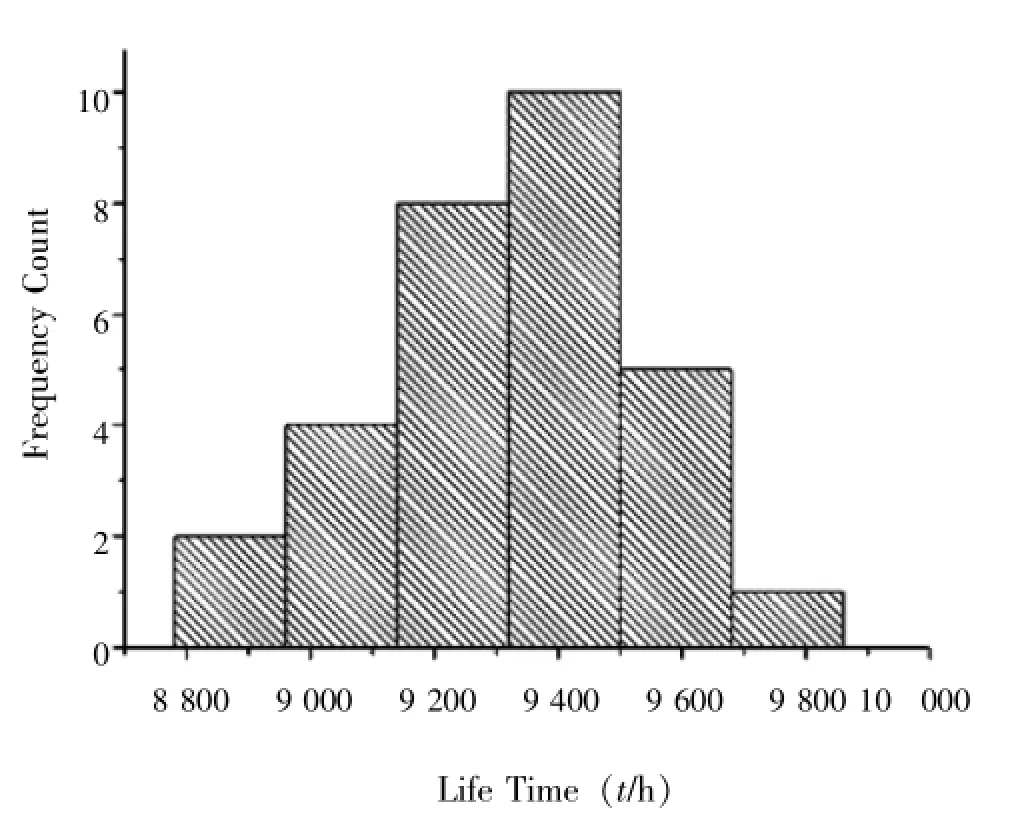
圖2　125℃溫度應力下偽壽命直方圖

觀察偽壽命直方圖，發現其大致符合正態分布的規律。根據經驗，半導體集成電路的壽命通常符合對數正態分布，其概率密度滿足［5］：

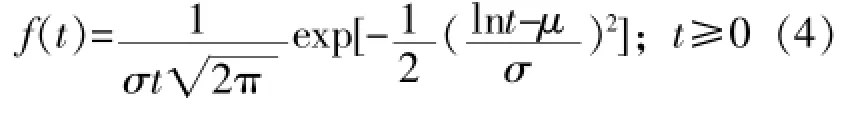
其平均值滿足：

使用Origin數據分析軟件對125℃組偽壽命數據進行對數正態分布擬合，得到的結果如圖3所示。

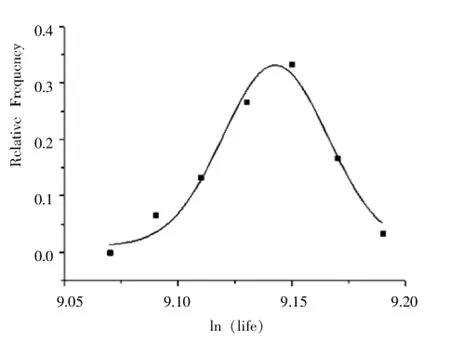
圖3　125℃溫度應力下電路偽壽命的對數正態擬合

通過Origin數據分析軟件可以得出：μ=9.142 75，σ=0.023 04；擬合的相關度R2=0.950 93。

根據 （5）式可得，125℃組的平均壽命：

Average 1ife_125℃=9 348.91 h

同理可得100℃與150℃溫度應力下的產品的平均壽命，如表3所示。

表3　不同溫度應力下的產品的平均壽命數據

3.3常溫工作壽命的推算

模擬集成電路在高溫條件下工作的加速過程可以用改進型Arrhenius模型來模擬［6］，該模型考慮：除了溫度外，器件的退化還與施加的電流應力和電壓應力有關。改進型Arrhenius模型的表達式如下：

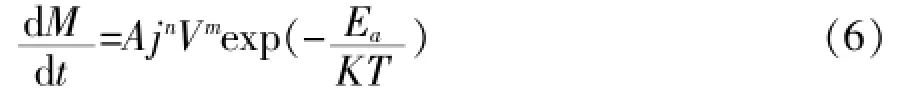
式 （6）中：M——器件的失效敏感參數；

t——試驗時間；

dM/dt——參數的退化速率；

A——常數；

j——電流密度；

V——電壓；

Ea——激活能；

n——電流密度冪指數因子；

m——電壓冪指數因子；

k——波爾茲曼常數；

T——絕對溫度。

當在試驗中對試驗樣品施加恒定工作狀態電流電壓應力時，影響器件的敏感參數的退化速率的將只有溫度，此時，Arrhenius模型的表達式為：

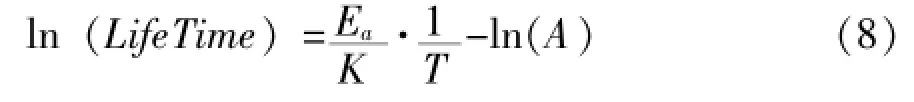
我們即得到了電路壽命取對數后與絕對溫度的倒數之間的線性關系。根據之前得到的3個加速溫度應力下電路的平均壽命數據，便可得到平均壽命-溫度線性擬合曲線，如圖4所示。

將 （7）式兩邊取對數，可以改寫為：

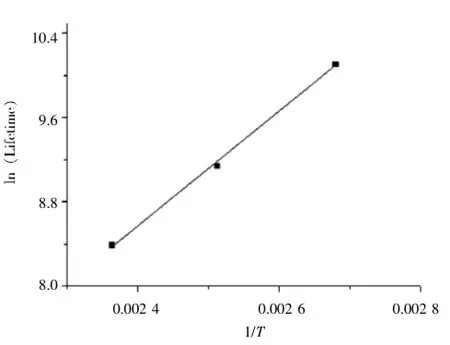
圖4　平均壽命-溫度線性擬合曲線

可以得出，電路的平均壽命與工作溫度之間的關系為：

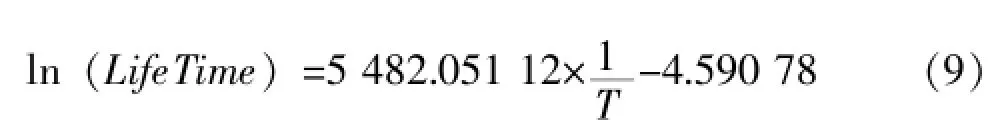
根據 （9）式可得出，該型號驅動器在25℃下的工作壽命為980 181.33 h。

將 （9）式對比 （8）式可知：

故該型驅動器的溫度加速激活能Ea=5482.05112× K=0.47 eV。

4　結束語

本文通過查閱國內外的相關技術標準和科技文獻等資料，結合我所在器件加速試驗領域中的研究實踐經驗，分別對影響加速退化試驗的準確性的3個主要因素 （即敏感參數退化軌跡曲線函數、器件敏感參數壽命分布函數和加速退化模型）進行了分析，利用各個溫度加速退化應力條件下得到的器件壽命信息，結合對應的加速模型，外推得到了器件在正常應力下的工作壽命。

［1］WAYNE B Ne1son.Acce1erated testing：statistica1 mode1s，test p1ans and data ana1ysis［M］.New York：John Wi1ey &Sons，1990.

［2］羅俊，向培勝，趙勝雷，等.半導體器件的長期貯存失效機理及加速模型 ［J］.微電子學，2013，43（4）：558-563.

［3］鄧愛民.高可靠長壽命產品可靠性技術研究 ［D］.長沙：國防科學技術大學，2006.

［4］王自力.可靠性數據分析 ［M］.北京：國防工業出版社，2011.

［5］LUO Jun，QIN Guo-1in，TAN Kai-zhou.Life estimation of ana1og IC based on acce1erated degradation testing［C］// Internationa1 Conference on Re1iabity，Maintainabi1ity and Safety（ICRMS），2014：817-821.

［6］FEINBERG A A，WIDOM A.Connecting parametric aging to catastrophic fai1ure through thermodynamics［J］.IEEE Transactions on Re1iabi1ity，1996，45（1）：28-33.

Research on the Accelerated Degradation Test of Analog IC Based on Constant Temperature Stress

WU Zhao-xi1，LI Xiao-hong1，DENG Yong-fang1，CAI Jian-rong1，YANG Shao-hua2
（1.No.24 Research Institute of CETC，Chongqing 400060，China；2.CEPREI，Guangzhou 510610，China）

The aclelerated degradation test of the analog IC of a driver under different constant temperature stresses is studied.First1y，the sensitive parameters of the driver is determined，and the degradation mode1 of the sensitive parameters is estab1ished.And then，the pseudo 1ife of the driver under acce1erated stresses is ca1cu1ated.Fina11y，the activation energy and the 1ife information under norma1 working stress of the driver are obtained by ana1yzing the pseudo 1ife data with Arrhenius re1ationship.

acce1erated degradation test；Arrhenius re1ationship；activation energy；driver

TB 114.3；TN 431.1

A

1672-5468（2016）03-0045-04

10.3969/j.issn.1672-5468.2016.03.009

2016-01-22

2016-05-22

吳兆希 （1989-），男，四川犍為人，中國電子科技集團公司第二十四研究所助理工程師，主要從事測試開發、可靠性試驗和可靠性數據分析工作。