再談浙江高考中的圓錐情結*
——以2道2016年浙江省數學高考文、理科卷填空題為例

●周筆崇　施剛良

(德清縣第三中學　浙江德清　313201)

?

再談浙江高考中的圓錐情結*

——以2道2016年浙江省數學高考文、理科卷填空題為例

●周筆崇施剛良

(德清縣第三中學浙江德清313201)

通過對2016年浙江省數學高考文、理科卷這2道填空題多種解法的探究，揭示出2道試題的共同本質：圓錐模型，高考試題的價值得到淋漓盡致的體現.

試題解答；本質透視；特殊化；圓錐模型

立體幾何是高中數學的核心內容之一，在培養學生的觀察判斷能力、空間想象能力、邏輯思維能力、運算推理能力等方面具有不可替代的重要性.因此，也就理所當然地成為數學高考常考常新的“寵兒”.

1　試題呈現

例1如圖1，在△ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的點P和線段AC上的點D，滿足PD=DA，PB=BA，則四面體PBCD體積的最大值是______.

(2016年浙江省數學高考理科試題第14題)

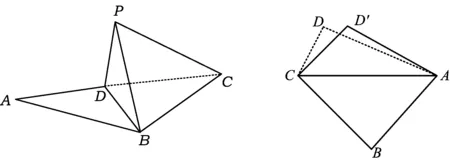
圖1 圖2

(2016年浙江省數學高考文科試題第14題)

評注立體幾何小題形式靈活、敘述簡潔，學生通過給定的圖形可以清楚地理解題目的意思.文、理科卷都是考查最值問題，這類題屬于壓軸題，對學生的要求比較高.學生可以從綜合幾何和向量幾何這2個方面加以解決，通過立體幾何這個載體，能有效地檢測學生的數學思維能力.

2　試題解答

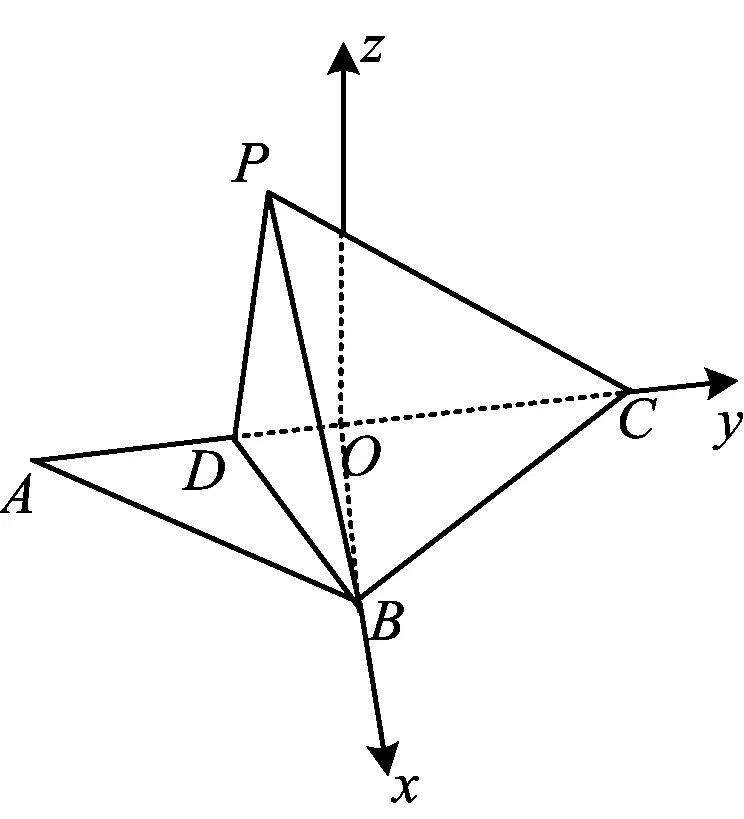
圖3

法國偉大的女數學家蘇菲說過：代數無非是寫出來的幾何，幾何無非是畫出來的代數.研究立體幾何問題，我們完全可以遵照蘇菲的說法，從坐標法和綜合幾何這2個方面來實施，這樣可以使得學生更加深刻地理解立體幾何的本質.

例1的2種解法如下：

PB2=(x-1)2+y2+z2=AB2=4,

(1)

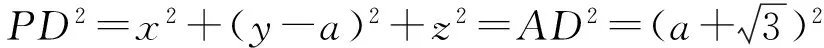
(2)

2式相減，得

將之代入式(2),整理得

(3)

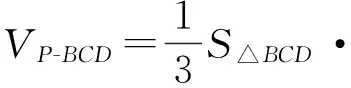
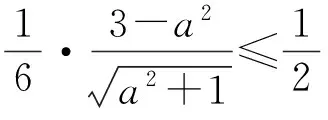
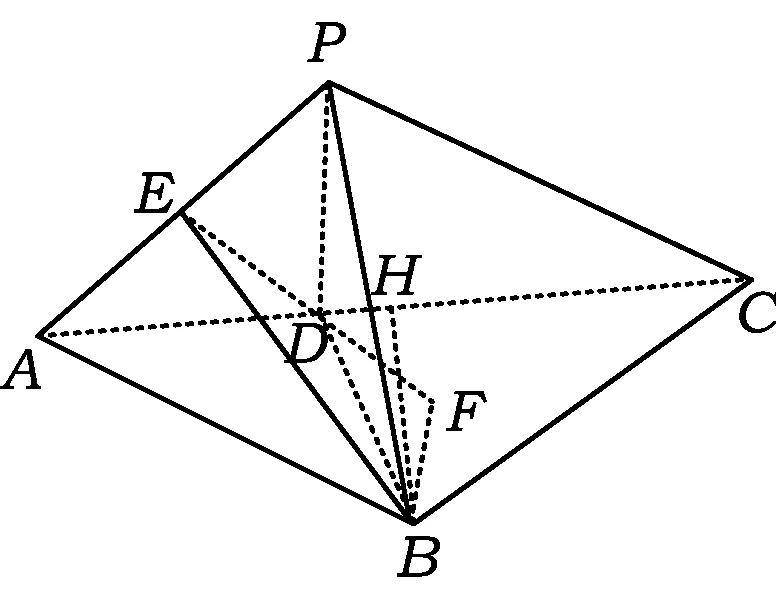
圖4

解法2依題意，如圖4，分別取AP，AC的中點E，H，聯結BE,DE,BH，則可以證明AP⊥面BDE，也即面APC⊥面BDE.過點B作BF⊥DE，垂足為F，于是

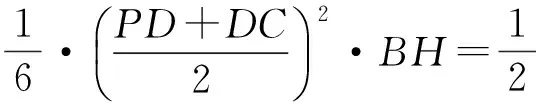
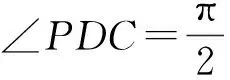
例2的2種解法如下：

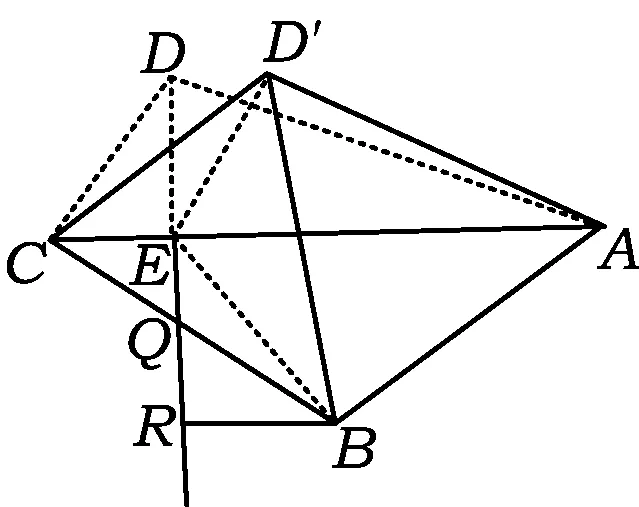
圖5

解法1與例1類似，建立空間坐標系，設已知點的坐標，將直線AC與BD′所成角的余弦用未知點D′的坐標表示出來，然后求出最大值，具體過程略，留給有興趣的讀者.

下面給出純向量解法：

解法2依題意，如圖5，過點D作DE⊥AC，聯結ED′,EB，再過點B作BR⊥DE，垂足為R,從而

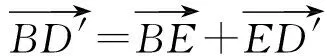
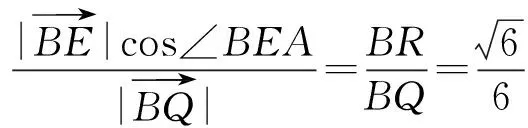
解到這里筆者還是意猶未盡，總感覺還有什么東西沒有揭示出來.立體幾何的本質問題就是幾何問題，從這個思路出發，可以揭示這2道試題的共同本質.

3　本質透視

著名數學家赫斯滕斯和索布齊克曾說過：沒有代數的幾何是啞巴，沒有幾何的代數是瞎子.由于我們沒有看清立體幾何錯綜復雜的點、線、面的位置關系，就會感覺立體幾何很難，找不到切入點，就像一個瞎子一樣，摸不清準確的方向.如果能看透問題的本質，形勢就一片明朗.而看透這2個立體幾何試題的本質，還是要靠立體幾何本身呈現的信息.

例1中題干“BP=BA=BC”暗示著我們可以聯想圓錐模型，如圖6，BA,BC是2條固定的母線，∠BAC是圓錐B-O這2條母線所成角的最大角，而BP是在動的母線，由此我們可以找到解題的突破口，即此題的幾何本質已浮出水面.要使VP-BCD達到最大，只要VB-PCD達到最大即可，而借助圓錐模型我們發現：三棱錐B-PCD的高是已知的即為BO，而△PCD面積的最大值上面已經算過，借助這個模型，此題基本可以“秒殺”.

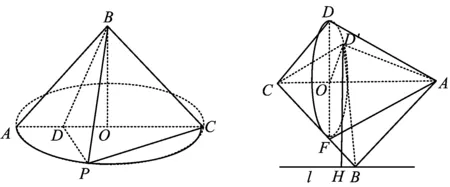
圖6 圖7

例2中提供的信息：已知平面四邊形ABCD，沿直線AC將△ACD翻折成△ACD′.這個信息非常關鍵，因為它還是會讓我們聯系到圓錐模型(而且是雙圓錐模型)[1]，如圖7,通過簡單的計算可知：

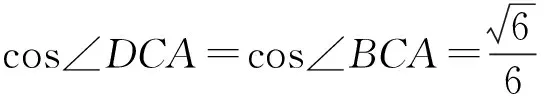
這也是圓錐模型的重要信息.過點B作l∥AC，此時，點D′在圓錐的底面上轉動，它在直線l上的投影點是不動點H.而直線AC與BD′所成角為∠D′BH，于是

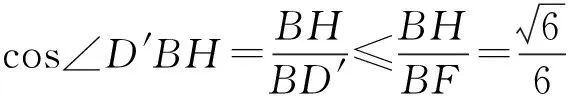
探究到這里我們發現，例1和例2的“祖宗”都是同一個：圓錐，以這個模型為背景在2015年浙江省數學高考理科試題第8題和文科第7題同樣考過[1].只是表述的方式不同，本質都是一樣的.透過現象看透問題的本質，這是我們研究數學的最高境界.

4　2點體會

4.1培養學生從特殊情況看問題

2016年浙江省數學高考理科卷的難度與2015年相當，文科難度較大，對學生的數學思維能力的考查要求較高，社會上再次議論紛紛.例1可以從筆者提供的2種解法入手，但考后通過調查，發現學生都不是這樣解決的，特別是解法1，運算量極大.學生通過取特殊位置把點D直接取AC的中點H，此時高的最大值即為BH，馬上就可以秒殺！關于例2，筆者給出了2種向量法：一種建系法，一種純向量法.但文科生不學空間向量，因此這2種解法對他們來說根本想不到.學生當然還是可以從特殊位置出發將答案做出來，通過估計當點D′轉到點F時，所成異面直線的夾角最小，余弦值達到最大，照樣秒殺！當然，學生從特殊位置處理問題，求得答案還是要冒一定的風險.

這需要我們在平常的教學實踐中，不斷地給學生滲透特殊化的思想.很多數學題目，特別是選擇題、填空題都可以用特殊值或特殊位置法解決，但是要真正掌握數學的本質，還是要將特殊轉化成一般，達到特殊與一般互相轉化.

4.2培養學生的建模意識

從2015年和2016年的浙江省數學高考立體幾何小題我們可以發現，利用圓錐模型的思想解決問題是多么重要[1].如果學生能抓住這個模型，這些題可以“秒殺”，也就不會認為它們是“難題”了.2016年的立體幾何小題延續了2015的考法，由此我們感嘆命題者對圓錐這個模型的情結有多深！在立體幾何的教學中，要不斷地滲透模型化的思想.隨風潛入夜，潤物細無聲，通過長時間的熏陶，學生就會很自然地利用模型來解決問題，做到以不變應萬變，這才是學生要學到的真本領.

[1]宋文泉，施剛良.浙江高考中的圓錐情結——透視高考立體幾何命題的本質[J].中學教研(數學)，2015(8):47-48.

*收文日期：2016-06-12；2016-07-05

周筆崇(1978-)，男，海南儋州人，中學一級教師.研究方向：數學教育.

O123.2

A

1003-6407(2016)08-40-03