平面向量基本定理的教學困境和應對策略*

●鄧　城

(增城中學　廣東廣州　511300)

?

平面向量基本定理的教學困境和應對策略*

●鄧城

(增城中學廣東廣州511300)

通過教學中的習題測評發現學生在“平面向量基本定理”的理解和應用上存在較大問題，經過對教材中向量知識編排結構的梳理和對學生認識規律的把握，提出了突破平面向量基本定理的教學難點的教學策略.

平面向量基本定理；基底；轉化；遷移

1　問題的提出

平面向量基本定理說明了平面中的任一向量都可以用2個不共線的向量線性表示，定理的形式化表達展現了數學的嚴謹性和邏輯性，它的出現也使得向量能夠真正地作為一種工具來準確描述現實世界中的“量”.可見，高中數學必修4的“平面向量”這一章節的核心內容就是“平面向量的基本定理”[1]，它為整個向量的內容起到承前啟后的作用.平面向量基本定理本身的確是容易理解的，但是否意味著學生都能很好地掌握呢？筆者選取了一組題目考查學生的掌握情況.

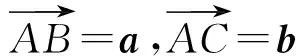
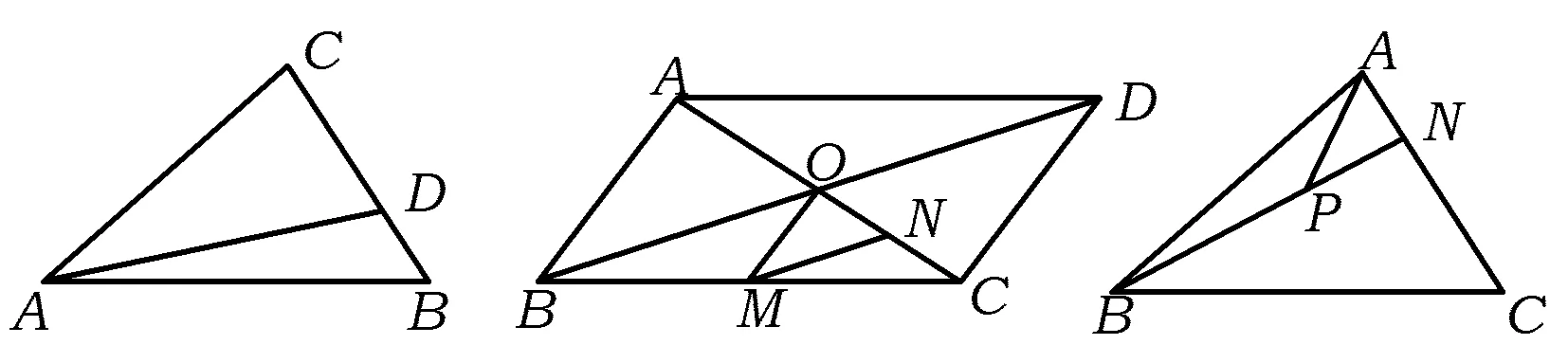
圖1 圖2 圖3

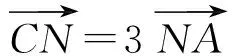
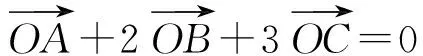
通過學生的作業反饋發現:第1)小題絕大多數學生都能做對，第2)小題也只有小部分學生做錯，但第3)小題只有不到一半的學生做對，第4)小題和第5)小題做對的更是寥寥無幾.

2　對教學時間和安排的反思

學生對平面向量基本定理的掌握情況不好，是否是因為教學用時不夠?單就“平面向量的基本定理”這一課程內容來說，只需要1個課時就足夠了，但其反映的思想和要求以及學生獲得的能力卻不是一蹴而就的，學生對它的掌握需要一個循序漸進、螺旋上升的過程.由于高一第2學期要上完《數學4》和《數學5》，教學時間緊，有些教師為了趕進度，再加上簡單地認為平面向量基本定理夠“簡單”，一個課時就搞定“平面向量的基本定理”和“平面向量的正交分解及坐標表示”(甚至更多內容)，課堂教學中對平面向量基本定理的產生缺乏足夠的舉例鋪墊，和盤托出結論，舉1～2個例題就算完成教學任務了.像這樣的教學“快餐”學生自然是消化不良的，一碰到難題就不知所措了.如此縮短課時固不可取，但是延長時間在那里“磨”也是不切實際的.

稍微熟悉教材就可以發現:平面向量基本定理在“向量數乘運算及其幾何意義”中已經涉及到，例如課本上的例7就要求用a，b表示某些向量，課后習題也有類似題目，只不過沒有點明其中隱藏的平面向量基本定理.可以說它為“平面向量的基本定理”的自然出現作了鋪設.而其后的“平面向量的數量積”中許多問題需要用到基本定理的應用.基于“平面向量的基本定理”承前啟后的特點，筆者認為優化該內容的教學需要站在整個章節的角度通盤考慮，將平面向量基本定理的教學滲透到前后的內容中去.

3　突破平面向量基本定理的教學難點的教學策略：一明一暗2條線

明線是在“向量數乘運算及其幾何意義”中培養學生對向量用2個不共線向量進行表示的方法，打好基礎；在“平面向量的基本定理”中強化各種向量表示方法，形成能力；在“平面向量的數量積”中注意平面向量基本定理的遷移運用，完善思想.暗線是遵循“從特殊到一般，從一般再到特殊”的教學思路，讓學生在特殊與一般之間體會轉化與化歸的數學思想.

3.1巧設鋪墊，打好基礎

在“向量數乘運算及其幾何意義”中，可以在課本例7的基礎上再設置幾個向量分解的例題，如：

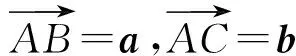
變式1若D為BC邊上的三等分點(靠近點B)時如何表示？

變式2若D為BC邊上的n等分點呢？

3.2典例訓練，強化技能

通過前面特殊向量分解的鋪墊，學生對“平面向量的基本定理”中任一向量的分解應該是非常清楚的，對定理的感性認識不成問題，困難在于落實到對復雜圖形背景下向量的有效準確分解時，學生還不熟練，甚至心理上很沒底.因此教師可以設置一些中等難度的向量分解題型，強化一般向量分解的訓練，當然更重要的是對學生碰到問題時給予必要的引導，并重視問題解決后的反思總結.

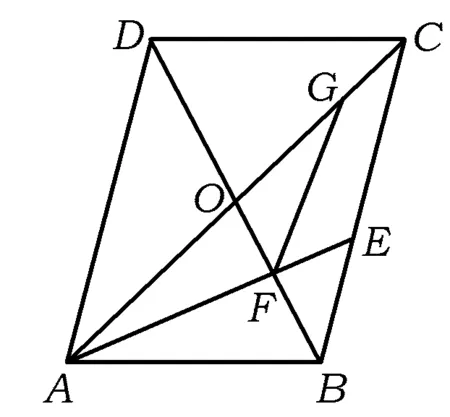
圖4

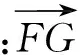
師：那大家能一下看出怎么表示嗎？

生：前面講過的方法2，即用三角形法則將向量先用其他向量表示，再繼續轉化為用a，b表示.

……

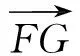
3.3遷移應用，完善思想

我們常說數學教學是為遷移而教[2]，在教授“平面向量的數量積”后要讓學生善于利用平面向量定理來解決向量中的各種問題，培養學生利用平面向量基本定理來轉化問題的思想，形成新的一種數學技能.

例如有些題目表面上問的是數量積怎么求，但實際上考查的是平面向量基本定理的應用.

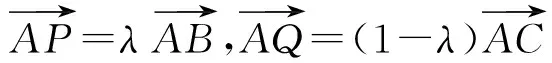
(2012年天津市數學高考試題)

另外，對定理的特殊情形進行討論研究有助于對定理的更深刻理解，也才能真正讓學生對定理的應用做到揮灑自如、恰到好處！例如：

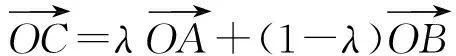
這個性質是平面向量基本定理的特殊情況，在高考試題中出現了好多次.但是很多學生在做題時不記得有這個特殊性質，費了很多時間才用其他方法做出來.究其原因還是對平面向量基本定理的特殊情況認識不夠.

[1]人民教育出版社課程教材研究所.普通高中課程標準試驗教科書·數學4(必修)[M].北京：人民教育出版社,2007:60-65.

[2]曹才翰，章建躍.數學教育心理學[M].北京：北京師范大學出版社,2006:257-260.

[3]陳重陽.也談向量法解決立體幾何問題[J].中學教研(數學)，2015(9)：17-20.

*收文日期：2016-05-12；2016-06-15

廣州市教育科研協作基地資助項目“課堂教學改革科研基地”(14XZ19)

鄧城(1983-)，男，廣東梅州人，中學一級教師.研究方向：數學教育.

O123.1

A

1003-6407(2016)08-01-03