基于神經網絡-模糊PID的軋機非線性扭振智能控制

韓東穎，李冰洋，時培明

（1.燕山大學 車輛與能源學院，河北 秦皇島 066004；2.燕山大學 電氣工程學院，河北 秦皇島 066004）

?

基于神經網絡-模糊PID的軋機非線性扭振智能控制

韓東穎1，李冰洋2，時培明2

（1.燕山大學 車輛與能源學院，河北 秦皇島 066004；2.燕山大學 電氣工程學院，河北 秦皇島 066004）

針對軋機傳動系統扭振控制問題，建立含間隙非線性的軋機系統動力學模型。考慮到軋機扭振模型的非線性和參數不易測量的特點，提出神經網絡和模糊PID相結合的控制器設計方法，以模糊PID為主體，通過引入神經網絡改變模糊隸屬度函數的中心值和寬度，最終得到最佳PID參數。設計神經網絡-模糊PID智能控制器，并利用實際軋機參數與經典雙閉環控制系統進行對比仿真。仿真結果表明所設計的智能控制系統對軋機傳動系統扭振的抑制作用明顯優于經典雙閉環控制系統。

振動與波；軋機傳動系統；扭振；間隙非線性；神經網絡；模糊PID

隨著軋機裝備水平的提高，軋機傳動已由先進的交流調速取代了傳統的直流調速，大大提高了軋機傳動的技術性能指標。但軋機大多利用原機械設備，機械與電氣配合不好，容易出現傳動系統的扭振現象，引起系統動態速降，甚至破壞控制系統的穩定性。另一方面，扭振會使傳動部件產生疲勞損傷，降低部件的使用壽命。劇烈的振動還會引起部件的突然破壞性斷裂，造成嚴重的經濟損失［1］。

隨著現代控制理論的發展，尤其是智能控制的出現，為扭振的抑制提供了新的思路。Orlowska-Kowalska T、Kaminski M利用經過OBD技術優化的神經網絡狀態觀測器來實現對軋機扭振的控制［2］。東北大學馬慶增在滑模變結構控制的基礎上引入模糊控制，實現了較為有效的扭振抑制［3］。為了實現更好的控制效果，本文提出神經網絡和模糊PID控制器相結合的方法，設計了神經網絡-模糊PID智能控制系統，并與經典雙閉環控制系統對軋機進行對比仿真。仿真結果表明設計的智能控制系統對軋機傳動系統扭振的抑制作用明顯優于經典雙閉環控制系統。

1　軋機傳動系統的扭振模型

軋機傳動系統是一個由若干慣性部件和彈性部件構成的“質量彈簧系統”。由于電機轉子和軋輥的質量遠大于其他部件的質量以及影響產品質量和系統動態響應品質的主要部件也是電機和軋輥，因此將軋機傳動系統看成是由電動機、軋輥以及連接兩者的彈性連接軸組成，也就是通常所說的軋機二質量系統，如圖1所示。

圖1軋機二質量系統模型

圖1中，M1是電機輸出轉矩；M2是軋輥負荷轉矩；M12是連接軸扭矩；ω1是電機角速度；ω2是軋輥角速度；J1是電機轉動慣量；J2是軋輥轉動慣量；θ1是電機旋轉角度；θ2是軋輥旋轉角度；K12是連接軸彈性系數。

根據運動學方程式寫出微分方程式得

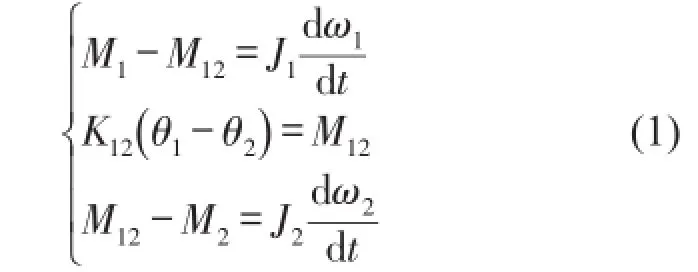
設θ1=∫ω1dt，θ2=∫ω2dt，代入式（1）得

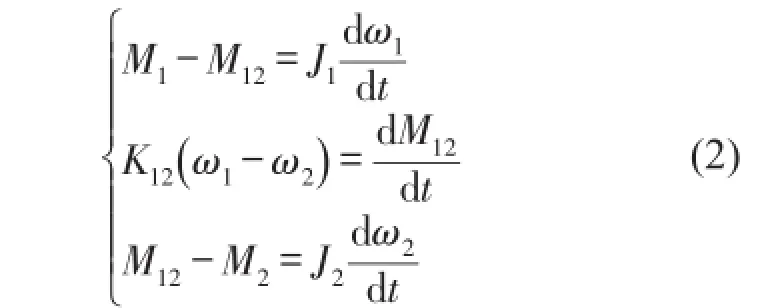
對式（2）進行拉式變換，得

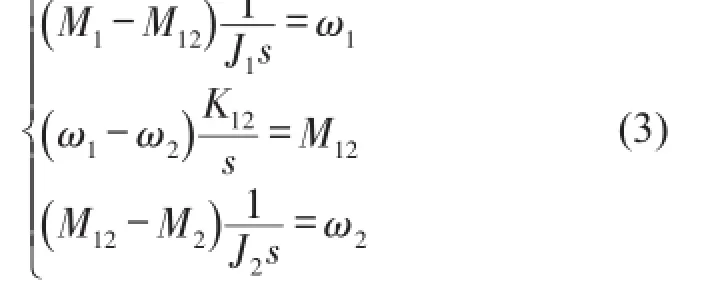
從式（3）可以寫出從電機轉速ω1到連接軸扭矩M12的傳遞函數T為

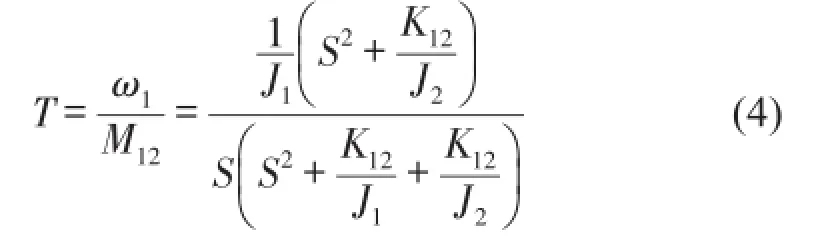
為了更貼近實際軋機，進一步建立含間隙非線性的二質量系統模型。在考慮軋機傳動系統結構間隙的扭振響應計算過程中，將彈性恢復力做分段線性化處理。將分段線性彈性恢復力代入沒有間隙時的扭振響應計算模型進行求解，就可得到含有間隙時的扭振響應［4］。

含間隙的軸系扭矩表示為

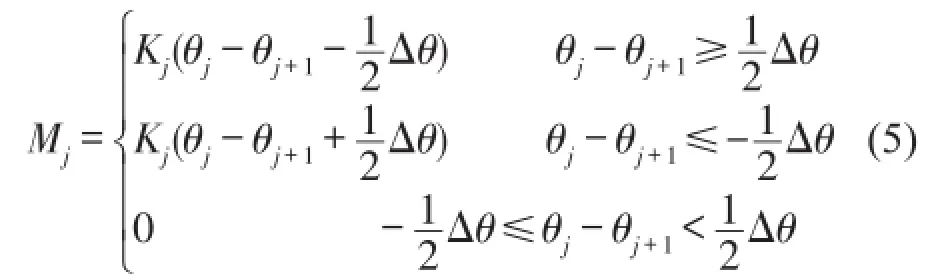
式中Kj——無間隙時的扭轉剛度；

θj-θj+1——角位移；

Δθ——間隙量。

根據上式建立含間隙非線性的軋機二質量系統模型，如圖2所示。

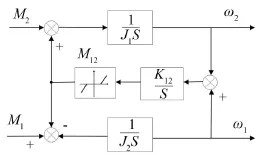
圖2　含間隙軋機二質量系統框圖

2　神經網絡-模糊PID軋機扭振智能控制器的原理和結構

2.1控制器的原理

神經網絡-模糊PID控制器是在模糊PID控制器的基礎上加入神經網絡［5］，也可以理解為模糊PID控制器和神經網絡兩部分組成了文中的神經網絡-模糊PID控制器，將系統的偏差與偏差的變化率輸入到神經網絡中，根據預設的模糊規則控制器，輸出對應于PID控制器的三個可調參數KP、KI、KD，然后控制系統對控制結果進行評價并反饋到神經網絡中，經網絡通過自學習與加權系數的調整，更新模糊控制的隸屬度函數，直到輸出最佳的PID控制參數［6］。

2.2控制器的結構

神經網絡選用BP神經網絡，BP模糊神經網絡模型模型如圖3所示，分為5層。

第一層是輸入層，它的作用就是將輸入值傳到第二層；第二層是隸屬度函數生成層，它的作用就是計算上一層的輸入分向量屬于本層各語言變量值的隸屬度函數；第三層是模糊推理層，每個節點都對應一條模糊規則，本層要計算出每條規則的適用度；第四層是歸一化層，實現的是歸一化計算。第五層是精確化輸出層，用來進行清晰化的計算。

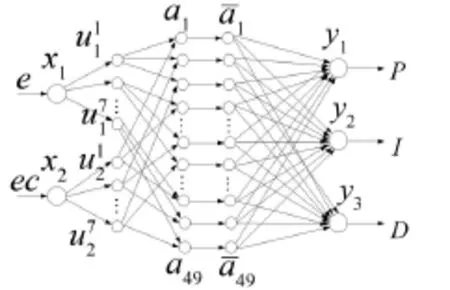
圖3　控制器結構圖

3　神經網絡-模糊PID軋機扭振智能控制器的設計

3.1模糊PID的原理

采用由誤差和誤差導數組成的二維模糊控制器。模糊控制器的設計需要經歷三個過程：模糊化、模糊推理和清晰化，控制原理圖如圖4所示。

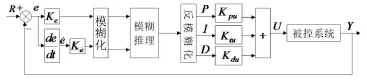
圖4　模糊PID控制原理圖

3.2模糊論域與隸屬度函數

模糊語言變量為誤差e和誤差導數e˙，其論域值為［-4，4］，變量為［NB，NM，NS，ZE，PS，PM，PB］，即負大、負中、負小、零、正小、正中、正大。PID三個參數KP、KI、KD論域取［1，2］，變量為［PE，PS，PM，PB，PL］，即零、正小、正中、正大、正最大。

采用高斯型的隸屬度函數，在設計時，通常在誤差為零處附近的形狀比較陡，以獲得良好的靈敏度，而在誤差大的區域則讓形狀較緩，以保證較強的魯棒性。初始設定值時，令誤差e和誤差導數e˙的設置相同，參數KP、KI、KD的設置相同。

3.3模糊規則的確定

模糊規則是模糊模控制器的核心，其設計離不開對系統定性的分析，設計前首先要定性地給出誤差與誤差變化率和PID三個參數直接的關系。以階躍信號的響應為例，給出每個階段對應的PID參數調節要求，如圖5所示。

按照誤差與誤差變化率的正負值和大小，可以把曲線主要分為七段，即AB、BC、CD、DE、EF、FG、GH。在AB段，e＞0，e˙＜0，其中誤差是主要考慮因素，為了使誤差能盡快減小以提高系統的響應時間，應給較大的P值（PL），而I和D則可以取較小的值或零（PE）。

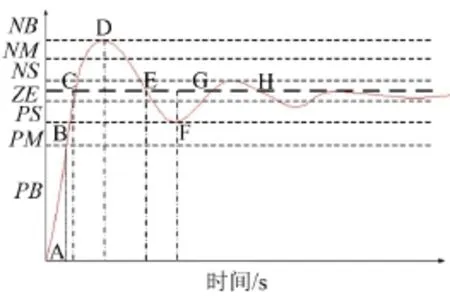
圖5　階躍響應下的系統曲線

在BC段，同樣e＞0，e˙＜0，由于之前的P值較大，系統以較快的速度上升，為了減小或者避免系統的超調量，此時應該把P值減小為PB，并且隨著e的減小，P值也應相應減小為PM，同時還應增大I與D的取值以減小超調。

在CD段，此時e＜0，e˙＜0，這個階段主要目標是控制系統的超調量，使曲線快速停止上升，所以要取較大的I值（PL），同時P取適中值（PM）。

在DE段，此時e＜0，e˙＞0，這個階段的主要目標是使曲線快速回落，并將誤差控制在較小的范圍。此時，P取中值（PM），I適當減小（PM），D取中大值（PM或PB）使系統有較好的抗干擾能力。

在EF段，此時e＞0，e˙＞0，為了保證穩態精度，P取中小值（PM），I取較小值（PS），D取中值（PM）。

在FG和GH段，此時e和e˙值已經接近于零，這個階段的主要目標是精調。此時誤差的積分幾乎不變，因此I取零值（PE），同時P和D取較小值（PS）以保證系統的穩態精度。

根據以上的分析，可以繪制出模糊控制的規則表，誤差與誤差變化率的模糊子集均為7個，故共有7×7=49條規則。模糊規則如表1所示［7］。

3.4精確化輸出

模糊規則確定后，開始模糊推理，求解模糊關系方程產生相應的模糊矢量。采用Takagi-Sugeno型推理，之后是將得到的模糊結果精確化，即解模糊，采用中位數法（Bisector）。最后就可以得到輸入為e和e˙下的P、I、D輸出。

3.5神經網絡的設計和訓練

神經網絡的訓練是在Matlab/Anfisedit中進行的，網絡類型選用BP網絡，分為五層［8］。訓練和檢測的數據從上面設計的模糊PID中提取。接著，生成模糊推理系統，完成后得到模糊神經網絡的結構。訓練初次生成的模糊神經網絡，誤差值設為0.03，訓練次數為1 000次。如果訓練一次達不到要求，就要對網絡的進行多次訓練直到達標為止。

表1　模糊推理規則表

4　基于神經網絡-模糊PID軋機扭振控制系統仿真分析

仿真實驗中用到的軋機參數是承鋼1 780 mm板帶軋機的實際參數，具體參數為：電機轉動慣量J1=13×10-4kg?m2、軋輥轉動慣量J2=18×10-4kg?m2、連接軸彈性系數K12=27 200N?m/rad、阻尼系數ζ=0.02。模糊神經網絡部分用的是上節訓練完成的網絡，通過編寫S函數實現［9］；軋機部分用的是含間隙非線性軋機二質量系統。在0 s處加單位階躍模擬軋機起振，在3 s處突加單位階躍模擬軋機扭振，為了更清晰顯示神經網絡-模糊PID的優越性，讓其跟經典雙閉環控制系統進行對比，分別取連接軸扭矩和軋輥轉速兩個量進行比較。

（1）連接軸扭矩在訓練中誤差曲線如圖6所示。

圖7中上半部分代表的是在雙閉環控制系統中連接軸扭矩仿真曲線，下半部分代表的是在神經網絡-模糊PID控制系統中連接軸扭矩仿真曲線。對比上下兩線可以明顯看出，不論是在起振階段還是在3 s處突加單位階躍負載的扭振階段，下線振蕩的頻率和幅度都比上線要小得多，并且下線更為平緩。

（2）軋輥轉速波動在訓練中誤差曲線如圖8所示。

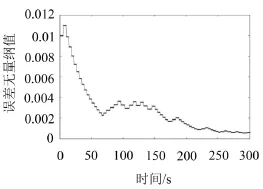
圖6　連接軸扭矩在訓練中均方根誤差曲線

圖7　連接軸扭矩對比圖

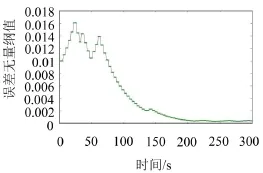
圖8軋輥轉速波動在訓練中均方根誤差曲線

圖9是軋輥轉速波動對比圖，上圖是雙閉環控制系統軋輥轉速波動仿真圖，下圖是文中神經網絡-模糊PID控制系統軋輥轉速波動仿真圖。可見，從起振的超調量到3 s處突加單位階躍時的動態速降，下圖轉速波動都比較小，并且恢復時間也短。

5　結語

通過對軋機系統的分析，建立更接近實際軋機系統的含間隙非線性軋機二質量系統模型。考慮到扭振模型比較復雜和參數不易測量的特點，建立神經網絡-模糊PID軋機扭振智能控制系統。最后，為了突出該系統的優越性，讓其和經典雙閉環控制系統在Matlab/Simulink環境中進行對比仿真，結果表明設計的神經網絡-模糊PID軋機扭振智能控制系統對軋機扭振有著更明顯的抑制效果。

圖9　軋輥轉速波動對比圖

［1］李崇堅，段巍.軋機傳動交流調速機電振動控制［M］.北京：冶金工業出版社，2003.

［2］ORLOWSKA-KOWALSKAT，KAMINSKIM.Application of the OBD method for optimization of neural state variable estimators of the two-mass drive system［J］. Neurocomputing，2009，72:3034-3045.

［3］馬慶增.軋機傳動系統扭振抑制滑模變結構控制器設計［D］.東北大學，2008：43-54.

［4］侯東曉，劉彬，時培明，等.分段非線性軋機輥系系統的分岔行為研究［J］.振動與沖擊，2010，29（12）：132-135.

［5］王益群，王海芳，高英杰，等.基于神經網絡PID的軋機AGC力控制［J］.中國機械工程，2005，16（18）：1650-1653.

［6］SUN J，ZHANG D，LI X，et al.Smith prediction monitor AGC system based on fuzzy self-tuning PID control［J］. Journal of Iron&Steel Research International，2010，17（2）:22-26.

［7］陳志旺，李建雄，王洪瑞.模糊PI軋機位置閉環控制實驗研究［J］.中國機械工程，2007，18（11）：1277-1280.

［8］賈春玉，王英華，周會鋒.板形板厚綜合調節神經模糊智能方法的研究［J］.中國機械工程，2003，14（20）：1741-1744.

［9］李國勇.智能控制及其Matlab實現［M］.北京：電子工業出版社，2005，194-284.

Intelligent Control of Nonlinear Torsional Vibration of Rolling Mills based on Neural Network and Fuzzy PID

HAN Dong-ying1，LI Bing-yang2，SHI Pei-ming2

（1.College of Vehicles and Energy，Yanshan University，Qinhuangdao 066004，Hebei China；2.College of Electrical Engineering，Yanshan University，Qinhuangdao 066004，Hebei China）

A dynamic model for a rolling mill with backlash nonlinearity is established for torsional vibration control analysis of the rolling mill’s drive system.Considering the nonlinearity of the model and the difficulty in parameters measurement，a controller’s design method of combining neural network with fuzzy PID is proposed.In this method，the fuzzy PID is the dominant.By introducing the neural network to adjust the central value and width of the fuzzy membership degree function，the optimal PID parameters are obtained.Then，the intelligent control system of the neural network combined with the fuzzy PID is designed and simulated using the real rolling mall parameters and the parameters of the classic double loop control system.The results show that the designed intelligent control system can suppress the torsional vibration of the rolling mill drive system obviously better than that of the classical double loop control system.

vibration and wave；transmission system of the rolling mill；torsional vibration；backlash nonlinearity；neural network；neural network；fuzzy PID

TM341；TH113.1

ADOI編碼：10.3969/j.issn.1006-1335.2016.04.034

1006-1355（2016）04-0161-04+187

2016-02-25

國家自然科學基金資助項目（51005196）；河北省自然科學基金資助項目（E2012203194）

韓東穎（1978-），女，吉林省遼源市人，副教授，碩士生導師。主要研究方向為振動分析與控制、結構健康監測。E-mail:dongying.han@163.com

時培明（1979-），男，黑龍江省延壽縣人，副教授，碩士生導師，主要研究方向為機械系統智能監測與控制。