汽輪發電機計及雙因素非線性影響的功角特性

康錦萍，　劉曉芳，　徐英輝，　王靖

(1.華北電力大學 電氣與電子工程學院，北京 102206；2.中國電力科學研究院 計量研究所，北京 100192)

?

汽輪發電機計及雙因素非線性影響的功角特性

康錦萍1，劉曉芳1，徐英輝2，王靖1

(1.華北電力大學 電氣與電子工程學院，北京 102206；2.中國電力科學研究院 計量研究所，北京 100192)

為研究磁路飽和與磁場畸變雙因素非線對汽輪發電機功角特性的影響，利用有限元方法獲得發電機的有功和無功功角曲線，揭示計及雙因素非線性的電抗隨功角變化的規律，然后將分運行區間的飽和電抗用于功角特性解析法計算。研究結果表明，汽輪發電機計及雙因素非線性后，極限功角小于90°，極限功率下降，無功功率減小；隨著功角的增大，直軸電抗先增大后減小，交軸電抗變化不大，兩者差值可達到14%；與直接用有限元方法計算的功角特性進行對比，用分運行區間電抗的計算結果非常吻合，而用空載特性修正的飽和電抗的計算結果相差較大。研究結果可為同步發電機靜態穩定極限的確定和暫態穩定的判斷提供參考。

汽輪發電機；磁路飽和；磁場畸變；功角特性；飽和電抗

0　引　言

同步發電機靜態穩定極限的確定和暫態穩定的判斷等電力系統關心的問題都離不開功角特性，但一般均采用不考慮飽和的功角特性。實際運行中發電機飽和程度隨著運行工況的變化而改變，在某些非正常運行情況下，磁路飽和與磁場畸變程度要比額定運行狀態嚴重的多，因此有必要研究磁路飽和與磁場畸變雙因素非線性對功角特性的影響。

發電機的功角特性通常指有功功率隨功角變化的關系。文獻[1]給出受擾動后第一個振蕩周期內發電機功角與有功功率之間的關系，并計算加速面積和減速面積，推導出實時判斷發電機運行暫態穩定的方法。文獻[2]給出用發電機工況參數模型來計算定子的端部溫度，從而確定發電機在各種運行方式下的進相運行能力及PQ容量圖。文獻[3]用有限元方法計算了高壓發電機在額定電壓和額定勵磁電流時的功角特性，并研究分析其基本電抗隨功角變化的關系。文獻[4-6]有限元方法研究了磁路飽和對同步發電機的功角特性的影響。

大部分文獻都是針對發電機的有功功角特性進行研究，實際上發電機功角的改變也會引起無功功率的改變。陳磊等[7]指出發電機作為電力系統中主要的動態無功電源，其發出無功功率是否達到極限對維持系統電壓穩定性至關重要。發電機進相運行可解決電力系統無功過剩問題，文獻[8]研究了發電機進相運行對系統靜態穩定極限的影響。文獻[9]建立同步發電機無功容量曲線的一種可視化工具，方便研究不同參數變化對其的影響。文獻[10]提出用發電機無功容量曲線來同時分配有功和無功負荷的方法。文獻[11]以發電機安全運行極限為基礎，根據無功輸出能力把發電機運行域分為不同區域來計算無功容量費用。文獻[12]對比研究高壓電纜繞制的發電機有功和無功功角特性。文獻[13]用數值分析法研究了凸極同步發電機靜態穩定極限功率和極限功角隨試驗電壓及電氣參數的變化規律。可見發電機無功功率功角特性對于電力系統運行和穩定同樣重要。

本文以300 MW汽輪發電機為對象，采用有限元方法，研究端電壓為額定值時磁路飽和與磁場畸變雙因素非線性對有功和無功功角特性的影響，并獲得了計及雙因素非線性的電抗及其隨功角的變化規律，進一步將該電抗用于有功功角特性和無功功角特性的分析，為電力系統穩定分析提供準確依據。

1　計及雙因素非線性影響的功角特性

1.1磁場畸變

文獻[14]指出同步發電機的非線性特征會受到磁路飽和與磁場畸變雙因素非線性共同作用的影響。圖1給出300 MW汽輪發電機額定電壓下功角75°的磁場分布圖。圖中定子陰影部分表示磁導率μFe<50μ0的區域，轉子陰影部分表示磁導率μFe<20μ0的區域。

圖1　δ=75°時的磁場分布圖Fig.1　Magnetic distribution when δ=75°

從圖1可以看出，功角75°時合成磁場軸線偏向于q軸，轉子小齒大部分單元的磁導率都小于20μ0，達到高度飽和，此時磁力線不是沿半徑方向穿過氣隙，而是斜穿定轉子槽，磁力線所走的等效氣隙長度[15]為0.312 m(實際上氣隙長度為0.15 m)，磁場發生了畸變。

1.2計及雙因素非線性影響的功角特性

同步發電機的功角特性可用公式(1)計算，若為隱極發電機，有Xd=Xq。發電機同步電抗通常采用制造廠給定的不飽和值。

(1)

圖2給出300 MW汽輪發電機額定電壓UN和額定勵磁電流IfN時的有功功率功角特性，其中不計雙因素的功角特性用公式(1)計算，計及雙因素的功角特性采用1.3節的有限元方法計算。

從圖2可以看出，計及雙因素非線性后極限功率和極限功角都有所減小，計及非線性的極限功率比不計非線性的值小1.21%，極限功角從90°變為85°。

表1給出300 MW發電機額定電壓UN下不同勵磁電流時的極限功率及極限功角。

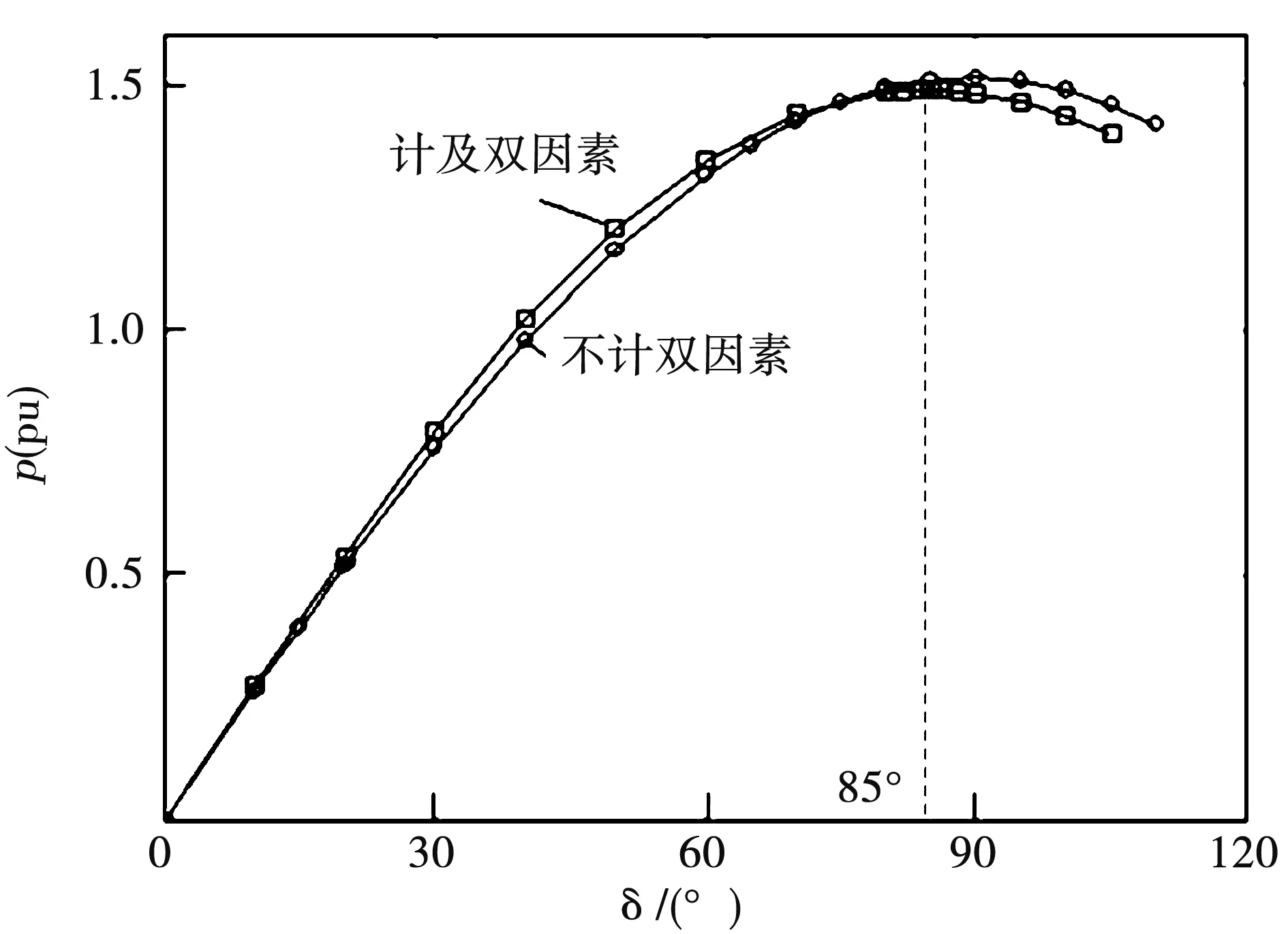
圖2　U=UN,If=IfN時的有功功角特性Fig.2　Active power angle characteristic under U=UN,If=IfN

勵磁電流極限功率極限功角不計雙因素計雙因素差值/%不計雙因素計雙因素0.8IfN1.20511.19560.7990.0083.00IfN1.50641.48811.2190.0085.002IfN3.01292.92223.0190.0088.00

從表1可以看出，不論勵磁電流的大小，只要計及雙因素非線性后，極限功率和極限功角都比不計非線性的值要小。隨著勵磁電流的增大，雙因素非線性對極限功率的影響增大，極限功角卻越來越接近于90°。

圖3給出300 MW汽輪發電機額定電壓UN和額定勵磁電流IfN時的無功功率功角特性。

圖3的計算結果表明雙因素非線性對無功功率功角特性影響較大，兩種情況下的特性曲線有明顯差異。當功角為0°時，不計雙因素非線性發出的無功功率為0.755，計及雙因素非線性發出的無功功率為1.050，兩者相差28%；發出無功功率為0的角度也存在很大不同，兩者相差12.1°。

1.3基于有限元的功角特性的計算方法

為了計及磁路飽和與磁場畸變雙因素非線性對功角特性的影響，可用有限元分析法進行磁場計算。當勵磁電流If和端電壓U確定時計算功角特性步驟如下：

1)給定某一小功角δ，給出電樞電流I和相位λ的初值進行磁場計算，得到端電壓Unew和功角δnew；

3)計算有功功率P=UIcosФ和無功功率Q=UIsinФ；

4)增大功角δ=δ+△δ，返回步驟1)進行下一功角的計算，直到算出功角特性。

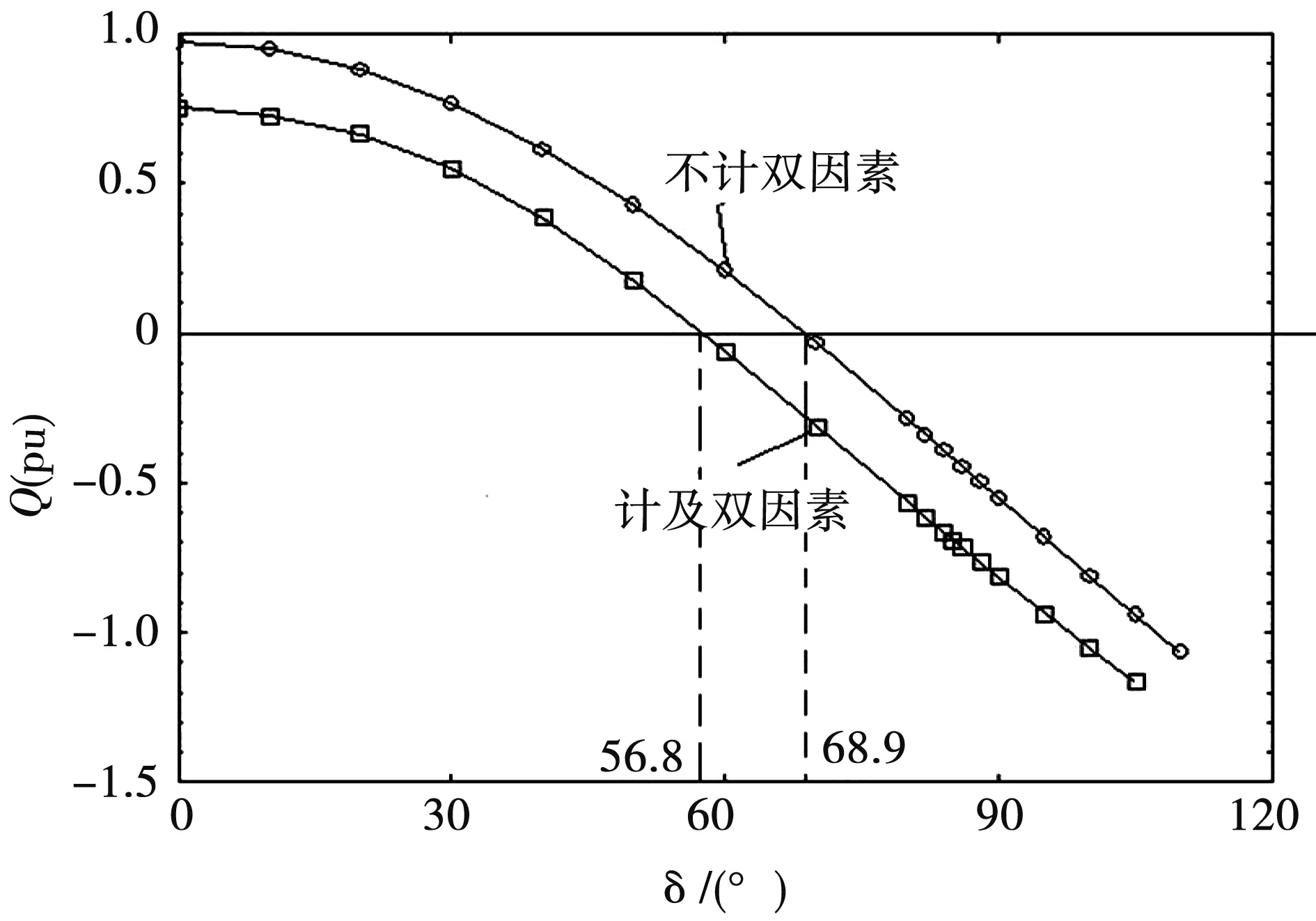
圖3　U=UN,If=IfN時的無功功角特性Fig.3　Reactive powercharacteristic under U=UN,If=IfN

2　計及雙因素非線性影響的電抗

2.1計及雙因素非線性影響的電抗的計算方法

發電機飽和電抗的計算方法傳統用空載特性得到飽和系數修正不飽和電抗得到。為了充分考慮負載運行條件的不同，后來發展到用有限元方法直接計算飽和電抗。IEEE[17]中給出用現場測量數據來獲取飽和電抗的方法，發電機端電壓U、定子電流I、勵磁電流If、功率因數cosφ、功角δ等量都可以測出，這樣就可畫出圖4所示的凸極發電機考慮飽和時的相量圖，圖中電抗Xds和Xqs都是飽和值。

圖4　凸極發電機考慮飽和時的相量圖Fig.4　Saturated phasor diagram of salient pole generator

圖4中d軸方向上有

(2)

圖4中q軸方向上有定義

(3)

發電機有限元磁場的二維數學模型能很好地考慮發電機磁路飽和與磁場畸變雙因素非線性。文獻[18 ]用有限元方法計算了發電機的勵磁電流，并與實測值對比，所有誤差都小于2%，驗證了有限元方法的準確性。如果沒有實測數據，可以用有限元方法計算公式(2)和式(3)中所需要的發電機電氣量，從而得到能計及雙因素非線性的電抗。

2.2汽輪發電機計及雙因素非線性的電抗

圖5給出300 MW汽輪發電機額定電壓UN和額定勵磁電流IfN時，飽和電抗X隨功角δ變化的關系，其中基于空載特性的飽和電抗Xc是用空載特性修正制造廠給的不飽和值得到，計及雙因素的Xd和Xq是用有限元方法和公式(2)和式(3)計算得到。圖6給出圖5運行狀態下的氣隙電勢Eδ隨功角δ變化的關系。

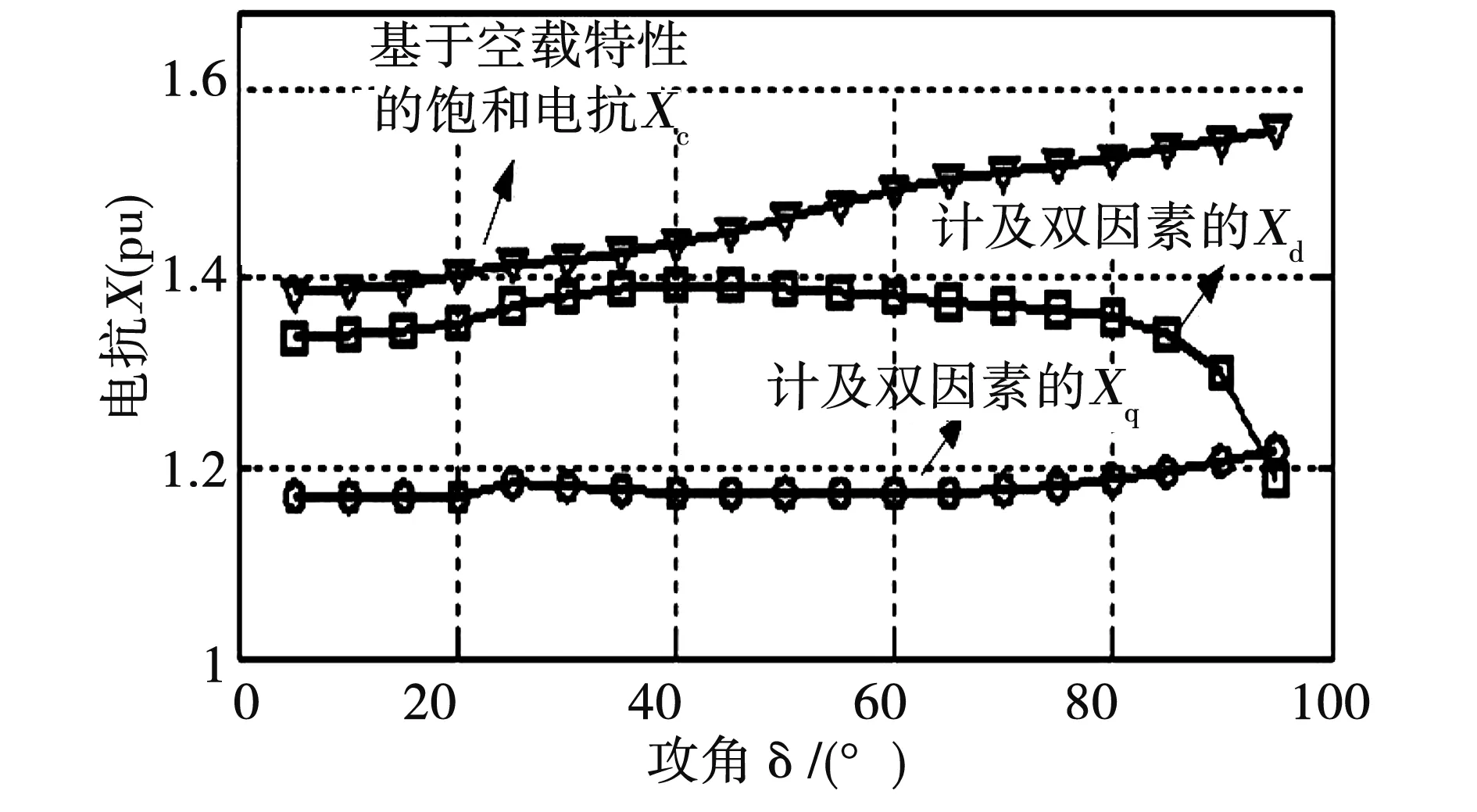
圖5　不同功角下的飽和電抗Fig.5　Saturated reactances when different angles

從圖6可以看出，當端電壓和勵磁電流固定時，隨著功角的增大，氣隙電勢Eδ下降，主磁路飽和程度下降，因此圖5中用基于空載特性飽和電抗Xc隨著功角的增大而增大，且不考慮隱極發電機d軸和q軸的差異；實際上，隨著功角的增大，主磁路飽和程度雖然下降，但磁場畸變程度使得等效氣隙增加，這樣就導致飽和電抗的變化不是單調上升的，如圖5所示計及雙因素電抗Xd，當功角小于40°時，主磁路飽和占主導地位，Xd有所上升，從1.33增加到1.39，增加了4.51%，當功角繼續增大，磁場畸變占主導地位，Xd又下降，從1.39 減小為1.30，減小了6.47%。電抗Xq介于1.17～1.19～1.20之間，變化較小。

圖6　不同功角下的氣隙電勢Fig.6　Air gap potential when different angles

3　基于雙因素非線性電抗的功角特性

1.2節的計算結果表明發電機雙因素非線性對發電機極限功角和無功功角特性有一定影響。因此計算功角特性時最好采用能計及雙因素非線性的電抗。表2給出圖5所示的不同功角范圍內平均飽和電抗，表中最后1列為用空載特性修正的飽和電抗。

表2　分區間的平均飽和電抗

將表2的分區間飽和電抗代入功角特性公式(1)計算，其中E0=XadsIf=(Xds-Xσ)If，xσ取常數，并與直接用有限元計算的功率進行對比，兩種方法計算的有功功率絕對差值△P如圖7所示，△P都很小。同樣用兩種方法得到的無功功率絕對差值△Q也很小。可見分區間飽和電抗能很好地反應雙因素非線性的影響。

圖8(a)和圖8(b)分別給出300 MW發電機用表1中分段飽和電抗代入公式(1)計算的有功和無功功角特性。

從圖8可以看出，用計及雙因素電抗計算的功角特性與用基于空載特性電抗計算的特性之間有較大差異，說明空載特性不能很好表征不同運行條件下的非線性特性。圖7計算結果指明計及雙因素的電抗計算的功角特性與直接用有限元方法的計算值幾乎相等。可見基于雙因素非線性飽和電抗的功角特性能更準確表征發電機的非線性特征。

圖7　兩種方法計算的有功功率之差△PFig.7　Active power differences between two methods

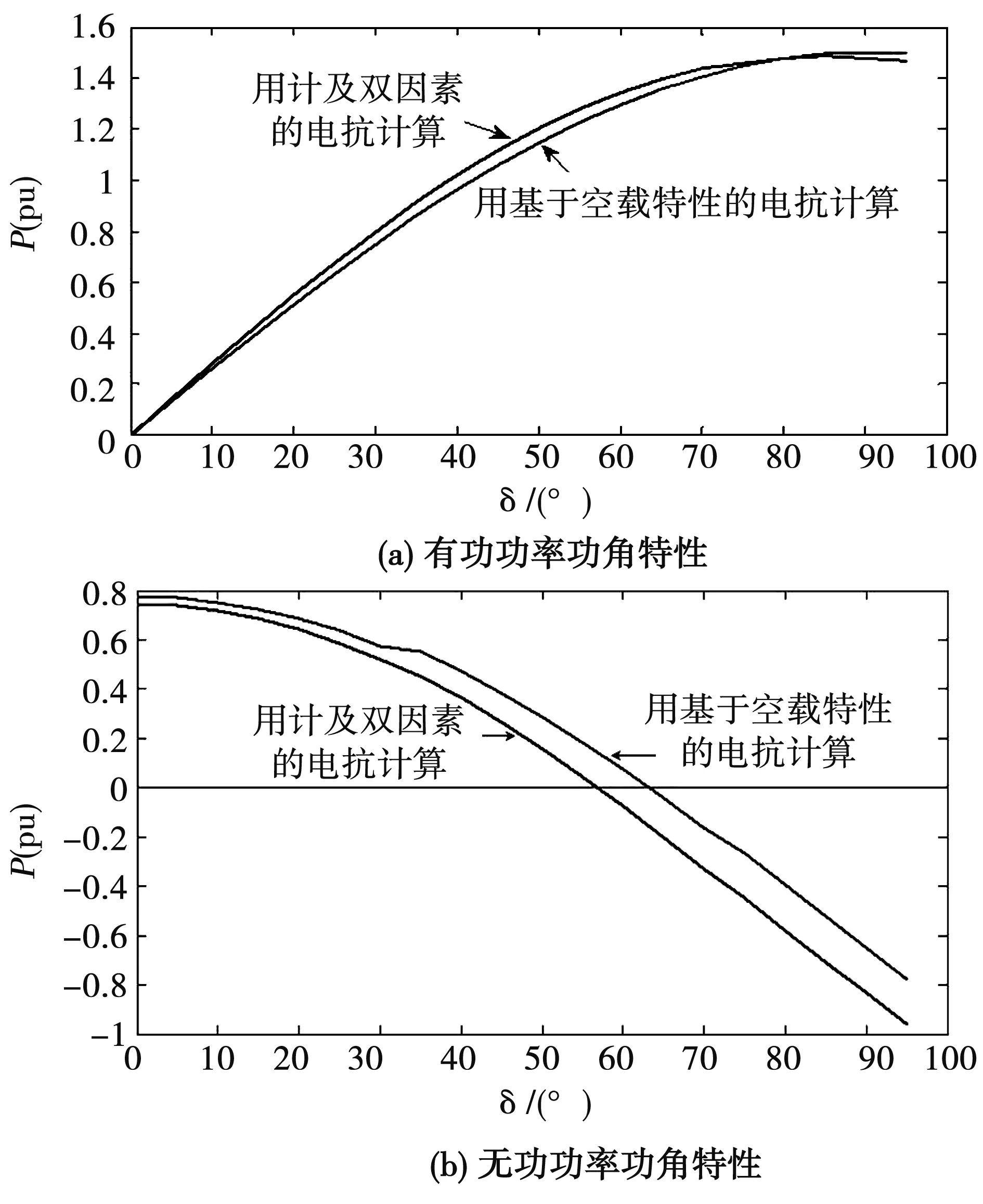
圖8　基于飽和電抗計算的功角特性Fig.8　Power angle characteristics based on saturated reactances

4　結　論

文中以有限元方法為工具，以300 MW汽輪發電機為對象，研究磁路飽和與磁場畸變雙因素非線性對發電機功角特性及參數的影響，得到結論如下：

1)汽輪發電機計及雙因素非線性后，不論勵磁電流的大小，極限有功功率都有所降低，極限功角都小于90°，無功功角特性與不計非線性的特性之間有較大差異。

2)當發電機端電壓和勵磁電流固定時，隨著功角的增大，氣隙電勢降低，用空載特性修正得到的飽和電抗單調增加，而計及雙因素的直軸電抗先上升后下降，交軸電抗變化較小。

3) 提出用計及雙因素非線性的分區間飽和電抗計算功角特性的方法，該方法能很好表征不同功角時磁路飽和與磁場畸變對非線性特征的影響，與直接用有限元方法計算結果幾乎重合在一起。

本文僅以1種典型汽輪發電機為研究對象，可以進一步擴展到多種汽輪發電機和水輪發電機，尋找適合電力系統使用的能計及發電機復雜非線性的功角特性，為電力系統準確分析提供依據。

[1]劉廣健，盧繼平. 基于功角特性曲線的發電機運行狀況實時分析 [J]. 電網技術，2006，30：41-45.

LIU Guangjian, LU Jiping.Real-time analysis of generator operation state based on power-angle curve [J]. Power System Technology, 2006，30：41-45.

[2]史家燕，史源素，趙肖敏，等. 發電機工況參數模型及進相運行在線監測 [J]. 中國電機工程學報，2006，26(11)：139-143.

SHI Jiayan,SHI Yuansu,ZHAO Xiaomin,et al．The new method of determining the capability of leading phase of generator and realizing the on-line monitoring [J]. Proceedings of the CSEE, 2006，26(11)：139-143.

[3]GE baojun, LIN Peng, TAO Dajun. et al. Calculation and analysis of saturated power angle characteristic and reactances variation for new high voltage generator[C]//2009 International Conference on Sustainable Power Generation and supply.Nanjing,China,April 6-7,2009:2312-2316.

[4]姚有光，湯蘊璆. 凸極同步電機飽和功角特性的數值計算[J]. 哈爾濱電工學院學報，1987，10(1):9-15.

YAO Youguang, TANG Yunqiu, Numerical calculation of saturated power angle characteristics of salient pole synchronous machine [J]. Journal of Harbin Institute of Electric Technology,1987，10(1):9-15.

[5]ZHOU Ji, LUO Yingli, CUI Xiang. Determination of power-angle curves of synchronous machines considering cross-magnetizing saturation effect [C]//Proceedings of 2000 IEEE PES Winter Meeting，Singapore，20001:228-232.

[6]史家燕，董明會，李惠升，等. 汽輪發電機的飽和功-角特性 [J]. 中國電機工程學報，1986，6(3):1-7.

SHI Jiayan, DONG Minghui, LI Huisheng, et al.Saturated power angle characteristic of turbogenerator [J]. Proceedings of the CSEE, 1986, 6(3):1-7.

[7]陳磊，閔勇. 發電機無功極限誘導分岔的機理分析及預防策略 [J]. 中國電機工程學報，2008，28(10)：14-19.

CHEN Lei, MIN Yong,Mechanism analysis and preventive measures investigation of generator reactive power limit induced bifurcation [J]. Proceedings of the CSEE 2008，28(10)：14-19.

[8]牟童，宋丹，葉峰. 計及靜穩極限的發電機進相運行能力研究 [J]. 東北電力技術，2010，10：7-11.

MAO Tong, SONG Dan,Capability study on generator leading operation considering static stability limit [J]. Northeast Electric Power Technology，2010，10：7-11.

[9]P. da Costa Jr., A. Nunes de Souza, P. S. da Silva,et. A Visual tool for building synchronous generator capability curves[C]//2012 Proceedings of IEEE Southeastcon, Orlando, Florida, USA, 15-18 March 2012: 1-6.

[10]XU Cheng，Frederick C. Huff，Peter Francino. Optimal load dispatch based on generator reactive capability curve[C]//IEEE Power Engineering Society General Meeting, 18-22 June 2006, Montreal, Quebec, Canada,2006: 22-26.

[11]余娟，顏偉，李文沅. 考慮發電機安全運行極限的非固定分段無功優化模型及其算法 [J]. 中國電機工程學報，2007，27(7)：23-28.

YU Juan, YAN Wei, LI Wenyuan.An Unfixed piecewise podel of reactive optimization and its algorithms considering generator capability limits [J]. Proceedings of the CSEE, 2007，27(7)：23-28.

[12]TAO Dajun, GE Baojun, Lü Yanling, et al. Systematically study on the static power-angle characteristics of a high voltage cable-wound generator prototype[C]//2009 International Conference on Sustainable Power Generation and supply. Nanjing,China,April 6-7, 2009:2236-2240.

[13]李志強， 何鳳軍， 晁暉. 進相試驗中凸極同步發電機靜態穩定限制的數值分析 [J]. 電機與控制學報， 2011，15(12):89-94.

LI Zhiqiang, HE Fengjun, CHAO Hui.Numerical analysis of steady state stability limit of salient synchronous generator in leading power factor operation test[J]. Electric Machines and Control, 2011, 15(12):89-94.

[14]羅應立，蒙亮，劉曉芳，等．汽輪發電機雙因素非線性特性的研究 [J]．電工技術學報，2005，20(6)：1-15

LUO Yingli，MENG Liang，LIU Xiaofang，et al．Study of two factors affecting nonlinear characteristic of turbogenerator [J]．Transactions of China Electrotechnical Society，2005，20(6)：1-5.

[15]張新麗，羅應立，康錦萍，等. 汽輪發電機內部非線性特征的定量表述 [J]. 中國電機工程學報，2007，27(24) ：74-78.

ZHANG Xinli，LUO Yingli，KANG Jinping，et al. The quantitative description of the nonlinear phenomena of the turbo-generator[J]．Proceedings of the CSEE，2007，27(24)：74-78．

[16]李志強，胡笳，祝麗芳，等. 同步發電機有限元磁場計算中端點量迭代的改進算法 [J]. 電工技術學報, 2008，23(12):35-41.

LI Zhiqiang, HU Jia,ZHU Lifang,et al. An improved iterative algorithm for terminal quantity of synchronous generator in FEM magnetic field [J].，Transactions of China Electrotechnical Society 2008, 23 (12) :35-41.

[17]IEEE Std 115-1995,IEEE Guide for Test Procedures for Synchronous Machines[S].

[18]康錦萍，劉曉芳, 羅應立，等. 不同容量汽輪發電機負載非線性特性的對比研究 [J]. 中國電機工程學報，2009，29(24):73-77.

KANG Jinping, LIU Xiaofang, LUO Yingli, et al．Research on the nonlinear load characteristics of different capacity turbine generators [J]. Proceedings of the CSEE，2009，29(24):73-77.

(編輯：劉素菊)

Power angle characteristic of turbine generator considering two factors affecting nonlinear characteristics

KANG Jin-ping1,LIU Xiao-fang1,XU Ying-hui2,WANG Jing1

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China;2. Metrology Department, China Electric Power Research Institute, Beijing 100192, China)

To study power angle characteristic of turbine generator considering two factors of iron saturation and magnetic field distortion affecting nonlinear characteristics, active and reactive power angle curves were obtained by the finite element method. The variation laws of saturated reactances considering two factors nonlinearity were revealed and these saturated reactances divided into different operating regions were used to analytical expressions of power angle curve. The research results show that power angle limit of turbine generator considering two factors is less than 90 degree and active power limit and reactive power are reduced. The direct reactance increases at first and then decreases with increase of power angles and quadrature reactance changes smaller and their differences are up to 14%. Comparing with power angle curves by finite element method(FEM), calculation results with saturated reactances in different operating regions are in good agreement and values with reactances based on no-load characteristic are very different.The research results can provide references for analyses of steady-state stability limit and transient stability.

turbine generator；iron saturation；magnetic field distortion；power angle characteristics；saturated reactance

2014-11-21

國家自然科學基金(51307049)

康錦萍(1975—)，女，博士，副教授，研究方向為電機的磁場分析；

劉曉芳(1961—)，女，教授，研究方向為電機運行與控制；

康錦萍

10.15938/j.emc.2016.08.003

TM 341

A

1007-449X(2016)08-0017-06

徐英輝(1972—)，男，碩士，高級工程師，研究方向為電氣測量與電機節能方面；

王靖(1971—)，女，碩士，講師，研究方向為電機運行及故障診斷。