任務(wù)驅(qū)動(dòng)法在遞歸算法教學(xué)設(shè)計(jì)中的應(yīng)用

楊平

（韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，廣東韶關(guān)512005）

任務(wù)驅(qū)動(dòng)法在遞歸算法教學(xué)設(shè)計(jì)中的應(yīng)用

楊平

（韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，廣東韶關(guān)512005）

摘要：遞歸作為一種編程算法在程序設(shè)計(jì)中廣泛應(yīng)用，是編程思維的重點(diǎn)內(nèi)容之一.以任務(wù)驅(qū)動(dòng)法在遞歸算法課堂教學(xué)中的應(yīng)用為例，設(shè)計(jì)趣味性任務(wù),由淺入深,激發(fā)學(xué)生的興趣，利用道具分解任務(wù)規(guī)模，促進(jìn)對(duì)問(wèn)題本質(zhì)的理解，旨在提高學(xué)生的學(xué)習(xí)興趣，培養(yǎng)學(xué)生的編程能力，提高教學(xué)質(zhì)量.

關(guān)鍵詞：遞歸算法；編程算法；課堂教學(xué)；編程能力

遞歸作為一種編程算法在程序設(shè)計(jì)中廣泛應(yīng)用，是指函數(shù)在運(yùn)行的過(guò)程中又直接或間接地調(diào)用該函數(shù)本身［1-2］.程序調(diào)用自身的編程技巧稱為遞歸，在函數(shù)中直接調(diào)用函數(shù)本身，稱為直接遞歸調(diào)用.在函數(shù)中調(diào)用其它函數(shù)，其它函數(shù)又調(diào)用原函數(shù)，這就構(gòu)成了函數(shù)自身的間接調(diào)用，稱為間接遞歸調(diào)用.

雖然用遞歸算法編寫(xiě)的程序結(jié)構(gòu)清晰存在著自調(diào)用過(guò)程，程序控制反復(fù)進(jìn)入其自身，使程序的分析設(shè)計(jì)有一定困難，致使很多初學(xué)者往往對(duì)遞歸迷惑不解，也在這上面花了不少的時(shí)間，卻收效甚微.本文以“任務(wù)驅(qū)動(dòng)法”來(lái)設(shè)計(jì)教學(xué)過(guò)程的內(nèi)容，首先從引人入勝的故事入手展開(kāi)教學(xué)，自然簡(jiǎn)單地引入遞歸概念，讓學(xué)生對(duì)知識(shí)點(diǎn)的認(rèn)識(shí)從感性到理性［3］.再?gòu)膶W(xué)生的角度出發(fā)合理地設(shè)計(jì)出學(xué)生能接受的教學(xué)內(nèi)容與環(huán)節(jié)，通過(guò)讓學(xué)生主動(dòng)分析遞歸算法經(jīng)典案例，結(jié)合教學(xué)道具促進(jìn)學(xué)生容易完成“教學(xué)任務(wù)”，從而達(dá)到培養(yǎng)學(xué)生主動(dòng)分析問(wèn)題、解決問(wèn)題的綜合能力.

1設(shè)計(jì)趣味性任務(wù),由淺入深,激發(fā)學(xué)生的興趣

課堂教學(xué)可以由一個(gè)古老的故事引入：從前有座山，山上有個(gè)廟，廟里有個(gè)老和尚和小和尚，老和尚給小和尚講故事，講的是:從前有座山，山上有個(gè)廟，廟里有個(gè)老和尚和小和尚，老和尚給小和尚講故事，講的是：從前有……

這是一個(gè)典型的“遞歸”故事，可以無(wú)限次遞歸下去.可以把這個(gè)故事比喻成遞歸調(diào)用，但在程序設(shè)計(jì)中，程序不可無(wú)限地遞歸下去，必須有遞歸結(jié)束條件，而且每次遞歸都應(yīng)該向結(jié)束條件邁進(jìn)，直到滿足結(jié)束條件而停止遞歸調(diào)用，同時(shí)適時(shí)宜地給出遞歸調(diào)用的定義.

遞歸調(diào)用的編程應(yīng)用有一個(gè)最著名的問(wèn)題：相傳在很久以前，在中東地區(qū)的一個(gè)寺廟里，幾個(gè)和尚整天不停地移動(dòng)著盤(pán)子，日復(fù)一日，年復(fù)一年，移盤(pán)不止，移動(dòng)盤(pán)子的規(guī)則是這樣的：事先固定三根針，假設(shè)分別為A針、B針、C針，A針上套有64個(gè)中間帶孔的盤(pán)子，盤(pán)子大小不等，大的在下，小的在上，要求把這64個(gè)盤(pán)子從A針移到C針，在移動(dòng)過(guò)程中可以借助于B針，每次只允許移動(dòng)一個(gè)盤(pán)子，且移動(dòng)過(guò)程中的每一步都必須保證在三根針上都是大盤(pán)在下、小盤(pán)在上.據(jù)說(shuō)當(dāng)所有64個(gè)盤(pán)子全部移完的那一天就是世界的末日，故漢諾塔問(wèn)題又被稱為“世界末日問(wèn)題”.

從給出這個(gè)著名的案例著手一步一步引導(dǎo)學(xué)生積極思考，從而自主找出解決問(wèn)題的方法，這樣的課堂的教學(xué)才能讓學(xué)生印象深刻，掌握遞歸本質(zhì).

2利用道具分解任務(wù)規(guī)模，促進(jìn)對(duì)問(wèn)題本質(zhì)的理解

課前簡(jiǎn)單制作出3個(gè)紙柱子與4個(gè)不同大小在空心紙盤(pán).首先給出一個(gè)最簡(jiǎn)單的情況，A針上只有一個(gè)盤(pán)，讓一個(gè)同學(xué)動(dòng)手操作如何去完成案例任務(wù).當(dāng)然任何一個(gè)學(xué)生就能完成：直接把一個(gè)盤(pán)從A針移到C針.

其次給出A針上只有2個(gè)盤(pán)，讓2個(gè)同學(xué)起來(lái)操作如何去完成任務(wù).可以適當(dāng)引導(dǎo)學(xué)生把任務(wù)分解成3步：（1）學(xué)生甲讓學(xué)生乙把A針上的一個(gè)盤(pán)從A針移到B針上.（2）學(xué)生甲直接把A針上剩下的一個(gè)盤(pán)子移到C針.（3）學(xué)生乙把B針上的一個(gè)盤(pán)從B針移到C針上.可以發(fā)現(xiàn)一共移動(dòng)了3=22-1次.

再給出A針只有3個(gè)盤(pán)，讓3個(gè)同學(xué)起來(lái)操作如何去完成任務(wù).可以適當(dāng)引導(dǎo)學(xué)生把任務(wù)分解成3步：（1）學(xué)生甲讓學(xué)生乙、丙把A針上的2個(gè)盤(pán)從A針移到B針上（用上的方法移動(dòng)了3次）.（2）學(xué)生甲直接把A針上剩下的一個(gè)盤(pán)子移到C針.（3）學(xué)生乙、丙把B針上的2個(gè)盤(pán)從B針移到C針上（用上的方法移動(dòng)了3次）.可以發(fā)現(xiàn)一共移動(dòng)了3+1+3=7=23-1次.

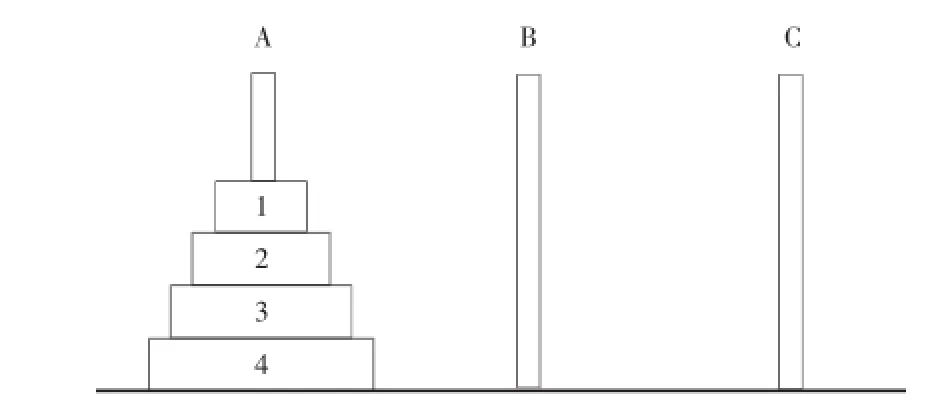
圖1　初始狀態(tài)　

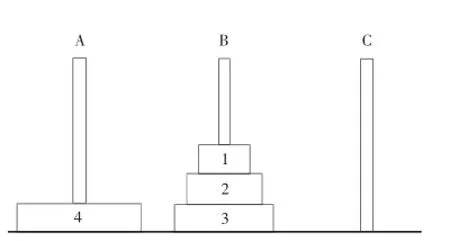
圖2　分解完成子問(wèn)題

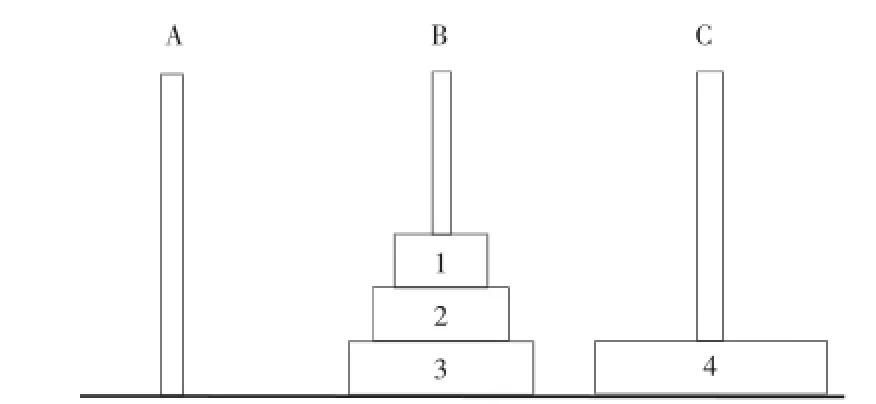
圖3　分解完成單步移動(dòng)

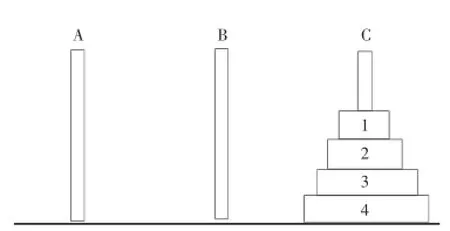
圖4　分解完成整個(gè)問(wèn)題

依次給出A針上只有4個(gè)盤(pán)的情況，如圖1～4所示.

利用前面每次的操作結(jié)果，同學(xué)們很快可以完成給定的任務(wù)，可以順其自然推理出：對(duì)于n個(gè)盤(pán)子需要移動(dòng)2n-1次，把64個(gè)盤(pán)子都移動(dòng)完畢約需1.8x1019次，假設(shè)每秒移動(dòng)一次，約需一萬(wàn)億年，不愧是世界末日問(wèn)題，地球壽命才100億年.目前，由于計(jì)算機(jī)運(yùn)算速度的限制，僅能找出問(wèn)題的解決方法并解決較小n值的漢諾塔問(wèn)題.

討論：漢諾塔問(wèn)題屬于非數(shù)值問(wèn)題，難以用數(shù)學(xué)公式表達(dá)其算法，可以從分析問(wèn)題本身的規(guī)律入手.第一步，問(wèn)題化簡(jiǎn)，設(shè)A針上只有一個(gè)盤(pán)子，即n=1，則只需將1號(hào)盤(pán)從A針移到C針.第二步，問(wèn)題分解，對(duì)于A針上有n（n＞1）個(gè)盤(pán)子的漢諾塔，可分為三個(gè)步驟求解：①將A針上n-1個(gè)盤(pán)子借助于C針移到B針；②把A針上剩下的一個(gè)盤(pán)子移到C針；③將B針上n-1個(gè)盤(pán)子借助于A針移到C針.

顯然，①、③兩步具有與原問(wèn)題相同的性質(zhì)，只是在問(wèn)題的規(guī)模上比原問(wèn)題有所縮小，可用遞歸實(shí)現(xiàn).

整理上述分析結(jié)果，把第一步作為遞歸結(jié)束條件，將第二步分析得到的算法作為遞歸算法，可以寫(xiě)出完整的遞歸算法描述.

定義一個(gè)函數(shù)movedisk（int n，char fromneedle，char tempneedle，char toneedle），該函數(shù)的功能是將fromneedle針上的n個(gè)盤(pán)子借助于tempneedle針移動(dòng)到toneedlee針，這樣移動(dòng)n個(gè)盤(pán)子的遞歸算法描述如下.

按照上述算法可編寫(xiě)出如下C語(yǔ)言程序：

3任務(wù)驅(qū)動(dòng)法教學(xué)內(nèi)容的展開(kāi)

適當(dāng)對(duì)遞歸調(diào)用教學(xué)內(nèi)容的展開(kāi)，在逐步求解的過(guò)程中培養(yǎng)學(xué)生的探索精神和分析、綜合歸納問(wèn)題的能力.引導(dǎo)學(xué)生探索遞歸調(diào)用編程在其他方面應(yīng)用，總結(jié)遞歸調(diào)用編程的通用方法與思維.

3.1數(shù)值問(wèn)題

可以表達(dá)為數(shù)學(xué)公式的問(wèn)題，如求斐波那契數(shù)列的第n項(xiàng)、求非負(fù)整數(shù)N的階乘、求兩個(gè)整數(shù)的最大公約數(shù)等.

首先來(lái)看一個(gè)數(shù)值問(wèn)題的遞歸算法的典型例子，斐波那契數(shù)列Fib（n）的遞推定義是：

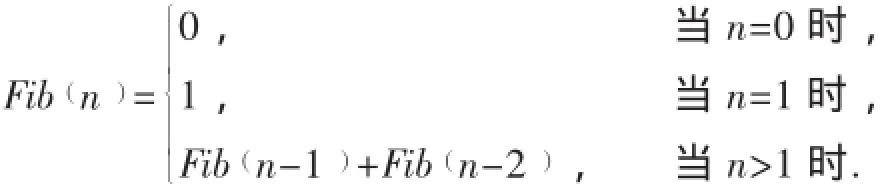
按照上式，求第n項(xiàng)斐波那契數(shù)列的遞歸函數(shù)如下：

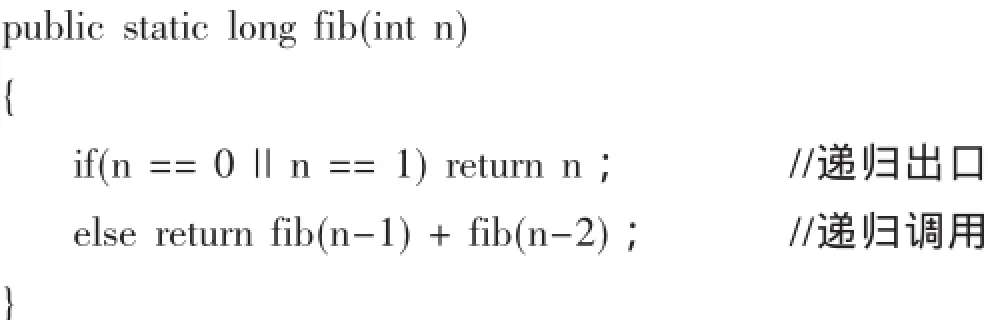
對(duì)于數(shù)值問(wèn)題，由于可以表達(dá)為數(shù)學(xué)公式，所以可以從數(shù)學(xué)公式入手推導(dǎo)出問(wèn)題的遞歸公式，然后確定問(wèn)題的邊界條件，從而確定遞歸的算法和遞歸結(jié)束條件.

3.2非數(shù)值問(wèn)題

對(duì)于本身難以用數(shù)學(xué)公式表達(dá)的問(wèn)題，如著名的漢諾塔問(wèn)題、八皇后、九連環(huán)問(wèn)題等非數(shù)值問(wèn)題，求解的一般方法是要設(shè)計(jì)一種算法，找到解決問(wèn)題的一系列操作步驟.如果能夠找到解決問(wèn)題的一系列遞歸操作過(guò)程，同樣可以用遞歸的方法解決這些非數(shù)值問(wèn)題，尋找非數(shù)值問(wèn)題的遞歸算法可以從分析問(wèn)題本質(zhì)的規(guī)律入手，可以按照下列步驟進(jìn)行分析：（1）將問(wèn)題進(jìn)行化簡(jiǎn)與最大限度縮小問(wèn)題規(guī)模，分析問(wèn)題在最簡(jiǎn)單情況下的求解方法與過(guò)程，這時(shí)的算法應(yīng)當(dāng)是最簡(jiǎn)單的非遞歸算法.（2）將問(wèn)題分解為若干個(gè)小問(wèn)題，其中至少有一個(gè)小問(wèn)題具有與原問(wèn)題相同的性質(zhì)，只是在規(guī)模上比原問(wèn)題有所縮小，將分解后的每個(gè)小問(wèn)題作為一個(gè)整體，描述用這些較小的問(wèn)題解決原來(lái)較大問(wèn)題的算法.由第（2）步得到的算法就是一個(gè)解決原問(wèn)題的遞歸算法，第（1）步將問(wèn)題的規(guī)模縮到最小時(shí)的條件就是該遞歸算法的結(jié)束條件.

最后引導(dǎo)學(xué)生總結(jié)遞歸程序設(shè)計(jì)的思維與原理，適宜于用遞歸算法求解的問(wèn)題的充分必要條件是：一是問(wèn)題具有某種可借用的類同自身的子問(wèn)題描述的性質(zhì)；二是某一有限步的子問(wèn)題有直接的解存在.

編寫(xiě)遞歸程序有兩個(gè)要點(diǎn)：一是要找到正確的遞歸算法公式，這是編寫(xiě)遞歸程序的基礎(chǔ)；二是要確定遞歸算法的結(jié)束條件，這是決定遞歸程序是否能正常終止的關(guān)鍵.

任務(wù)驅(qū)動(dòng)法課堂教學(xué)的最后，可以設(shè)計(jì)一些比較典型容易實(shí)現(xiàn)的任務(wù)，讓學(xué)生趁熱打鐵，通過(guò)完成任務(wù)，加深對(duì)教學(xué)內(nèi)容的掌握與理解.

4結(jié)語(yǔ)

遞歸算法在程序設(shè)計(jì)中十分有用.遞歸算法的實(shí)質(zhì)是把問(wèn)題轉(zhuǎn)化為規(guī)模縮小了的同類問(wèn)題的子問(wèn)題.然后遞歸調(diào)用函數(shù)來(lái)表示問(wèn)題的解.當(dāng)一個(gè)問(wèn)題蘊(yùn)含了遞歸關(guān)系且結(jié)構(gòu)比較復(fù)雜時(shí)，采用遞歸算法能使程序變得簡(jiǎn)潔和清晰，增加了程序的可讀性，并能夠很容易地解決一些用非遞歸算法很難解決的問(wèn)題.

以任務(wù)驅(qū)動(dòng)法來(lái)設(shè)計(jì)遞歸算法課堂教學(xué)內(nèi)容與過(guò)程，在任務(wù)驅(qū)動(dòng)教學(xué)過(guò)程中培養(yǎng)學(xué)生的探索精神和分析問(wèn)題的能力，激發(fā)學(xué)生的求知欲［3-4］，切實(shí)提高了課堂教學(xué)效果.

參考文獻(xiàn)：

［1］譚浩強(qiáng).C程序設(shè)計(jì)［M］.4版.北京：清華大學(xué)出版社，2010.

［2］嚴(yán)蔚敏，吳偉民.數(shù)據(jù)結(jié)構(gòu)（C語(yǔ)言版）［M］.北京：清華大學(xué)出版社，2004.

［3］唐大仕.“遞歸算法”微課教學(xué)設(shè)計(jì)——以“文科計(jì)算機(jī)基礎(chǔ)（下）”為例［J］.計(jì)算機(jī)教育，2013（17）：5-7.

［4］王婧.任務(wù)驅(qū)動(dòng)法在計(jì)算機(jī)課程教學(xué)中的應(yīng)用 ［J］.計(jì)算機(jī)教育，2011（8）：51-55.

（責(zé)任編輯：邵曉軍）

中圖分類號(hào)：TP399；G642

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1007-5348（2016）04-0075-05

［收稿日期］2016-03-01 ［基金項(xiàng)目］韶關(guān)學(xué)院教育教學(xué)改革研究項(xiàng)目（SYJY20131431）；韶關(guān)學(xué)院2013年度科研項(xiàng)目（韶學(xué)院〔2013〕205號(hào)）.

［作者簡(jiǎn)介］楊平(1977-),男,湖南臨湘人,韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院講師,碩士；研究方向：計(jì)算機(jī)應(yīng)用技術(shù).

Application of Task Driven Method in the Recursive Algorithm in Teaching Design

YANG Ping
（CollegeofMathematicsandStatistics，ShaoguanUniversity，Shaoguan512005，Guangdong，China）

Abstract:Recursionas aprogrammingalgorithmis widely usedinprogramdesign，whichis oneof thekey content of programming thinking.As an example，the application of task driven method in the recursive algorithm for classroomteaching，and designing interesting tasks，is easy to understand，to stimulate students’interest，to use props to decompose the scale of the task，to promote the understanding of the nature of the problem,in order to improve the students’interest in learning，to train students programming ability，and to improve the quality of teaching.

Key words:recursivealgorithm；programmingalgorithm；classroomteaching；programmingability