姿態融合濾波的無人機抗干擾控制算法*

陸興華

(廣東工業大學 華立學院，廣東 廣州 511325)

姿態融合濾波的無人機抗干擾控制算法*

陸興華

(廣東工業大學 華立學院，廣東 廣州 511325)

提出一種基于姿態融合濾波的無人機(UAV)抗干擾控制算法。分析無人機飛行的運動模型，構建無人機在飛行的姿態參量約束下的運動方程，設計擴展卡爾曼濾波器進行干擾濾波，實現飛行姿態參量信息融合，以捷聯慣導傳輸到執行器的姿態融合誤差為控制目標進行控制算法優化。仿真實驗結果表明:采用該方法進行無人機的姿態信息融合和控制，輸出的姿態信息參量具有較高的精度，誤差收斂到最小，控制性能較好，抗干擾能力較強，保障了無人機的穩定飛行。

無人機； 飛行控制； 姿態角； 濾波

0 引 言

傳統方法中，對無人機(UAV)[1]飛行控制的算法研究主要有基于模糊PID神經網絡控制的飛行控制算法、基于粒子群算法的無人機飛行控制算法，基于自適應噪聲抵消的飛行控制算法和基于智能仿生群控制的飛行控制算法等[2～5]。上述方法在進行無人機飛行控制設計中，只針對干擾強度較小的控制界面進行擾動校正，對強干擾下的無人機姿態穩定性控制的效果不好。對此，相關文獻進行了算法改進設計，其中，文獻[6]提出一種基于自適應反演積分的無人機飛行控制擾動誤差修正算法。建立無人機的縱向運動模型，在速度坐標系、體坐標系、彈道坐標系和地面坐標系中進行無人機的控制參量約束模型構建，得到無人機縱向運動數學模型和控制模型，但是該控制算法計算開銷較大，姿態穩定性控制受到不確定參量的影響較嚴重，需要進行算法改進設計；文獻[7]提出一種基于全局漸近跟蹤誤差補償和模糊PID變結構控制的飛行器控制設計方法，算法有效提高飛行控制的導向性和自適應制導性能，但該控制方法的誤差收斂性不好，抗干擾能力不強。

針對上述問題，本文提出一種基于姿態融合濾波的無人機抗干擾控制算法。首先構建無人機飛行的運動方程和控制對象模型，進行控制約束特征分析，以此為基礎構建控制目標函數，分析無人機在飛行中受到的影響因素，設計擴展卡爾曼濾波器(extended Kalman filter,EKF)進行干擾濾波，實現姿態參量信息融合，達到抗干擾控制算法改進設計的目的，最后通過仿真實驗進行了性能測試，得出有效性結論。

1 無人機飛行的運動數學模型和控制對象描述

1.1 無人機飛行的運動模型

(1)

無人機的空間運動是一個封閉的線性反饋過程，考慮模型的非線性特性和不確定性，使用歐拉角方法計算姿態角，通過對姿態特征進行線性自回歸分解，采用四元素方法求無人機陀螺儀的操舵信息參數，通過求得無人機飛行姿態角，在四元素組合下，構建運動坐標系，如下

(2)

同時，對系統某些參數進行測量，無人機的滑翔狀態下的縱向運動控制參量滿足微分方程

(3)

采用四階Runge-kutta法求解微分方程，再加上自適應律，計算無人機飛行運動的狀態特征更新值

(4)

式中h為自適應迭代的步長。代入歐拉角公式得到無人機飛行運動的姿態信息運動方程

θ=arcsin(-T31)

(5)

(6)

(7)

通過對上述運動方程的構建，在實際的運行過程中不斷地對系統某些參數進行測量，以此為數據基礎，進行控制執行機構的設計。

1.2 無人機抗干擾控制對象描述

在上述對無人機飛行的運動方程構建的基礎上，進行被控對象描述，分析無人機控制參量約束模型構建，將飛行的陀螺姿態角作為初始運動參量，受到干擾的偏差為ω(k)，對應無人機質心加速度的過程噪聲協方差Q；將飛行控制的點源陣列流型向量作為實時測量角度，偏航操縱的偏差為v(k)，對應的協方差為測量噪聲協方差R。出可以得出，無人機的縱向運動方程是一組由非線性微分方程組成的動力系統，無人機在進行控制參量采集中，采用陀螺儀、加速度計進行姿態信息融合和加速度信息采集[9]，得到無人機飛行中每一個方向對應姿態角θ(k)的狀態方程和測量方程Z(k)可以表示為

θ(k)=Aθ(k-1)+BU(k)+ω(k)

(8)

Z(k)=Hθ(k)+v(k)

(9)

式中A和B為自適應加權相關參數，H為無人機的控制測量參數，U(k)為k時刻無人機的線性擾動控制量。無人機控制狀態是建立在狀態變量和誤差協方差估計的基礎上，通過對姿態信息的融合濾波，采用干擾抑制算進行濾波器構建，得到無人機飛行狀態的預測方程

θ(k/k-1)=Aθ(k-1/k-1)+BU(k)

(10)

式中 無人機姿態角的均方誤差方程表示為

P(k/k-1)=AP(k-1/k-1)AT+Q

(11)

式中P(k/k-1)為θ(k/k-1)對應的無人機飛行控制的約束參量。無人機飛行控制狀態估計方程

θ(k/k)θ(k/k-1)+Kg(k)[Z(k)-Hθ(k/k-1) ]

(12)

式中Kg(k)為濾波增益。作用在無人機的總空氣動力的信道向量的增益方程

Kg(k)=(P(k/k-1)HT)/[HP(k/k-1)HT+R]

(13)

通過無人機飛行控制的約束參量分析，估計無人機航向的均方誤差方程

P(k/k)=[I-Kg(k)H]P(k/k-1)

(14)

(15)

假定系統在一定時間演變范圍內是收斂的，由于干擾向量的分布函數形式已知，當無人機處于任意姿態時，無人機飛行穩定性控制下的加速度值為

Ab=[axayaz]T

(16)

[axayaz]T=

(17)

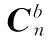
2 無人機抗干擾控制算法改進設計

改進算法的設計過程描述如下： 根據無人機的飛行狀態，進行姿態信息參量估計，則可計算出俯仰角和橫滾角

(18)

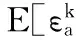
(19)

式中mx和my為離散系統差分信息在OXb軸、OYb軸上的分量；ψm為無人機在飛行過程中的磁北的航向角；Δψ為磁力計角度(磁偏角)；ψ為累積誤差，在縱軸OXb相對于真北的航向角上進行抗干擾抑制，得到輸出的控制執行舵機的相位角為

ψ=ψm+Δψ

(20)

無人機飛行過程中姿態會不斷變化，存在俯仰角θ和橫滾角γ。對測量組合系統修正

(21)

通過融合更新計算得到捷聯慣導傳輸到執行器的姿態融合誤差，在較大的噪聲誤差下，采用姿態融合和EKF設計，進行誤差跟蹤補償，得到在縱向飛行滑膜面上的相鄰兩時刻角度估計的差值

(22)

(23)

將兩式相減，動態加速度恒定的情況下，得到無人機飛行的兩時刻融合的誤差

(24)

通過干擾抑制，在給定頻帶上求得噪聲干擾的協方差

Cov(f,f)=E[(f-Ef)(f-Ef) ]=E[(f-Ef)2]

(25)

(26)

(27)

通過上述分析，求得無人機飛行控制的姿態融合信息，得到飛行控制律優化為

(28)

通過上式可見，采用本文設計的控制方法，經過不斷的卡爾曼濾波系數調整，可以使得姿態角的誤差收斂為零，提高控制精度，算法的實現過程描述如圖1所示。

3 仿真實驗與控制性能分析

首先構建無人機飛行控制仿真的硬件平臺，采用基于VXI總線的數據采集系統，進行飛行姿態數據采集，通過航向陀螺儀、執行舵機傳感器等設備進行原始的飛行姿態數據信息的采集，輸入到控制系統中進行飛行控制系統的數字信號處理。控制算法采用Matlab編程，進行控制程序設計和仿真，無人機飛行的俯仰角分別為Δ1=5°,Δ2=8°，假設擾動干擾的信噪比為0，快拍數為1 000，自適應參數ε1=0.1，采用本文算法(改進的EKF)和傳統的自適應EKF控制算法和基本EKF融合算法，進行性能對比，以無人機飛行控制的俯仰角、橫滾角、橫向角為測試指標，得到控制輸出結果如圖1所示。

圖1 無人機抗干擾控制輸出的性能測試Fig 1 Performance test of anti-disturbance control output of unmanned aerial vehicle

由圖可見：采用本文方法進行無人機的姿態信息融合，輸出的姿態信息參量具有較高的精度，控制性能較好，抗干擾能力較強。為了定量分析本文方法的控制誤差，以未加入干擾和加入干擾后的無人機飛行姿態參量的誤差為測試指標，得到仿真結果如圖2所示。

圖2 控制參量誤差分析Fig 2 Error analysis of control parameters

從圖可見：采用本文算法進行無人機飛行控制，誤差收斂到最小，控制品質較高，保障了無人機的穩定飛行。

4 結束語

構建無人機飛行的運動方程和控制對象模型，進行控制約束特征分析，構建無人機飛行控制目標函數，設計EKF進行干擾濾波，實現姿態參量信息融合，達到抗干擾控制算法改進設計的目的，研究結果表明:該控制方法進行無人機飛行控制的品質較高，姿態參量的誤差較小，穩定性較高，展示了較好的應用價值。

[1]ZhaoShilei,GuoHong,LiuYupeng.Faulttolerantcontrolforlineartime-delaysystembasedontrajectorytracking[J].InformationandControl,2015,44(4):469-473.

[2]MingPingsong,LiuJianchang.Consensusstabilityanalysisofstochasticmulti-agentsystems[J].ControlandDecision,2016,31(3):385-393.

[3]LiT,ZhangJ.Consensusconditionsofmulti-agentsystemswithtime-varyingtopologiesandstochasticcommunicationnoises[J].IEEETransonAutomaticControl,2010,55(9):2043-2057.

[4]MahmoudEE.Complexcompletesynchronizationoftwononidenticalhyperchaoticcomplexnonlinearsystems[J].MathematicalMethodsintheAppliedSciences,2014,37(3):321-328.

[5]PalomaresI,MartinezL,HerreraF.Aconsensusmodeltodetectandmanagenon-cooperativebehaviorsinlargescalegroupdecisionmaking[J].IEEETransonFuzzySystem,2014,22(3):516-530.

[6]DongBo,LiuKeping,LiYuanchun.Decentralizedintegralsli-dingmodecontrolfortimevaryingconstrainedodularandreconfigurablerobotbasedonharmonicdrivetransmission[J].ControlandDecision,2016,31(3):441-447.

[7]ElowitzMB,LeiblerS.Asyntheticoscillatorynetworkoftranscriptionalregulators[J].Nature,2000,403(20):335-338.

[8]MTi微慣性航姿系統/GPS組合技術研究[D].哈爾濱：哈爾濱工程大學，2009.

[9]TittertonDH.捷聯慣性導航技術[M]．2版.王秀萍,等，譯.北京：國防工業出版社，2007.

[10] 秦永元．慣性導航[M]．北京：科學出版社，2005.

Anti-interference control algorithm for UAV based on attitude fusion filtering*

LU Xing-hua

(Huali College,Guangdong University of Technology，Guangzhou 511325，China)

An anti-disturbance control algorithm for UAV based on attitude fusion filtering is proposed.Analyze UAV flight motion model,build equations of motion constrained by UAV flight attitude parameters,design extended Kalman filter for interference filtering,to achieve integration of flight attitude parameter information,taking attitude fusion error that strapdown inertial navigation transmitted to executor as control objectives to optimize control algorithm.Simulation experimental results show that using the method for UAV attitude information fusion and control and output attitude information parameters have high precision,error converges to the minimum,control performance is good,anti-interference ability is strong,which ensure stability of UAV flight.

UAV; flight control; attitude angle; filtering

10.13873/J.1000—9787(2016)07—0116—04

2016—05—06

2015年廣東省教育廳重點平臺及科研項目青年創新人才類項目(自然科學類)(2015KQNCX218)；2012廣東省質量工程項目(粵教高函[2012]204號)

TP 276

A

1000—9787(2016)07—0116—04

陸興華(1981-)，男，遼寧遼陽人，碩士，講師，主要從事計算機控制算法、圖形圖像方向的研究。