改進粒子濾波的無線傳感器網絡目標跟蹤算法*

丁婷婷， 高美鳳

(江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122)

改進粒子濾波的無線傳感器網絡目標跟蹤算法*

丁婷婷， 高美鳳

(江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122)

針對粒子濾波(PF)重采樣后造成的粒子枯竭現象的問題, 提出了一種基于改進重采樣的粒子濾波無線傳感器網絡目標跟蹤算法。該算法避免了殘差重采樣算法中的殘留粒子重采樣問題，減少了計算時間；通過產生新的粒子，增加了粒子的多樣性，從而改善了粒子枯竭現象。仿真實驗結果表明:改進重采樣的粒子濾波算法提高了目標跟蹤精度，降低了跟蹤誤差。

目標跟蹤； 無線傳感器網絡； 粒子濾波； 重采樣； 粒子枯竭

0 引 言

無線傳感器網絡(wireless sensor networks，WSNs)是由部署在監測區域內的大量成本低、體積小、具有一定通信與計算能力的傳感器節點組成，且節點之間通過無線通信的方式形成一個多跳的自組織網絡系統。相較于具有很高的可靠性、魯棒性、精確性，但價格昂貴的復雜檢測技術，例如：雷達、通用分組無線業務(GPRS)等，WSNs部署隨機，具有自組織性、魯棒性和隱蔽性，因此WSNs非常適用于目標的定位和跟蹤。在WSNs目標跟蹤中，常用的跟蹤算法有：擴展卡爾曼濾波(EKF)[1]、無跡卡爾曼濾波(UKF)[2]、粒子濾波(PF)[3]等。卡爾曼濾波算法在非線性系統中難以應用，擴展卡爾曼濾波適用于非線性化程度比較低的應用中，無跡卡爾曼濾波不能應用于非高斯分布系統。而粒子濾波算法利用粒子集來表示概率，所以,可以很好地解決一些非線性非高斯估計問題。由于目標跟蹤中目標的運動是不確定的，其實質是一種非線性問題，因此，粒子濾波廣泛應用于目標跟蹤。

粒子濾波存在的最大問題是粒子退化，為了避免退化，Arulampalam M S等人[4]提出重采樣方法，重采樣雖然一定程度上緩解了粒子退化現象，但同時會造成粒子枯竭現象。針對粒子枯竭問題，文獻[5]提出一種基于權值選擇的粒子濾波的目標跟蹤算法.該算法從眾多備選粒子中選出權值相對較大的粒子用于狀態估計，但易產生明顯的權值退化現象。文獻[6]是一種基于多通道多選擇(multiple-channel/multiple-choice,MCMC)粒子濾波算法，但該算法明顯增加了算法的計算時間。本文針對上述問題，從保持樣本多樣性和控制算法復雜度的角度出發， 提出了一種基于改進重采樣的粒子濾波WSNs目標跟蹤算法。其基本思想是：對粒子權重與總的粒子數的乘積累計求和后，再取整，求得累計粒子復制次數。當某個粒子被多次(大于1次)選取時，不再單純地根據求得累計粒子復制次數進行復制，而是將其和重采樣前的所有粒子的均值作為父代粒子用來產生新的粒子，然后將新的粒子用于下一時刻的迭代計算。

1 問題描述

WSNs由傳感器節點組成，所有節點隨機布置在監測區域內，每個傳感器節點位置已知。同時,傳感器節點之間可以進行無線通信,且每個節點都知道其鄰居節點的位置。

X(k)=ΦX(k-1)+GW(k-1)

(1)

Z(k)=HX(k)+V(k)

(2)

式中Φ為狀態轉移矩陣，G為過程噪音驅動陣，W(k-1)為過程噪音，其方差為Q，H為量測矩陣，V(k)為觀測噪音，理想情況下為零均值的高斯白噪音，其方差為R。

2 WSNs中改進粒子濾波目標跟蹤算法

2.1 目標跟蹤原理

WSNs中跟蹤目標時，處于偵測狀態的傳感器節點探測到目標之后，將探測到的信息數據包發送到匯聚節點。匯聚節點收到所有數據后進行數據融合，得出該物體是否是需要被跟蹤的物體。如果是需要被跟蹤的物體，將使用一種跟蹤運動目標的算法，隨著目標運動，跟蹤算法將及時通知合適的傳感器節點參與跟蹤。

2.2 改進的粒子濾波

粒子濾波的核心思想是利用一些離散隨機采樣點(粒子)來近似系統隨機變量的概率密度函數，以樣本均值代替積分運算，從而獲得狀態的最小方差估計[7]。粒子濾波算法在經過若干次迭代后，只有少部分的粒子具有較大的權值，而大部分粒子的權值很小，并趨向于零，這使得大量的運算時間耗費在對系統狀態估計作用不大的粒子上。解決該問題有兩種方法[8]：一種是選擇好的重要性概率密度函數；另一種是使用重采樣。在粒子濾波算法框架中引入重采樣方法可以有效緩解退化現象，常用的重采樣算法有多項式重采樣、系統重采樣、殘差重采樣等。不同于其他兩種常用的重采樣，殘差重采樣的粒子復制次數絕大多數并不必通過隨機數來求取。

殘差重采樣的實質是將各粒子的權值與1/N的整數倍進行比較，得到的數近似可以看做粒子復制次數，但不一定相等，所以存在殘留粒子重采樣問題，其具體步驟可見參考文獻 [9]。文獻[10]提出的改進的殘差重采樣的基本思想為：權重與總的粒子數的乘積累計求和后，再取整，求得累計粒子復制次數，可以保證重采樣前后粒子數目不變。采用此方法可以避免殘差重采樣造成的殘留粒子重采樣問題，降低運算的復雜度，從一定程度上減少了運算時間。但文獻[10]的重采樣僅僅避免了殘差重采樣造成的殘留粒子重采樣問題，不能減緩重采樣造成的粒子枯竭現象。所以,本文在借鑒文獻[10]基礎上，在重采樣的過程再增加粒子的多樣性，即當某個粒子被多次(大于1次)選取時，不再單純地進行復制，而是將其和重采樣前的所有粒子的均值 作為父代粒子，用來產生新的粒子。本文采用的改進殘差重采樣其具體步驟如下：

3)輸出子代粒子。

3 仿真實驗

在100 m×100 m的區域內，假定當前4個傳感器節點在感知范圍內跟蹤目標步長M=50,采樣周期T=1 s,對三種算法分別進行1 000次仿真，為比較算法的性能，采用均方根誤差(RMSE)[11]和平均誤差(ARMSE)[11]作為衡量跟蹤精確度的指標。

圖1(a)是本文改進算法與殘差重采樣粒子濾波算法、文獻[10]進的殘差重采樣粒子濾波算法跟蹤軌跡曲線。圖1(b)是目標勻速直線運動時三種算法跟蹤誤差曲線，在跟蹤誤差曲線圖中隨著時間的推移，粒子濾波跟蹤誤差逐漸增大，這是由于粒子枯竭等因素引起的。在25 s時文獻[10]中改進的殘差重采樣粒子濾波算法跟蹤誤差比殘差重采樣粒子濾波算法跟蹤誤差降低了21 %，本文改進算法跟蹤誤差比殘差重采樣粒子濾波算法跟蹤誤差降低了45.4 %。改進算法是三種算法中跟蹤誤差增加最緩慢的，由此可見，改進算法緩解了粒子枯竭現象。圖1(c)是目標勻速直線運動時三種算法運行時間曲線，盡管三種算法的運行時間動蕩不定，但均值相差不大。

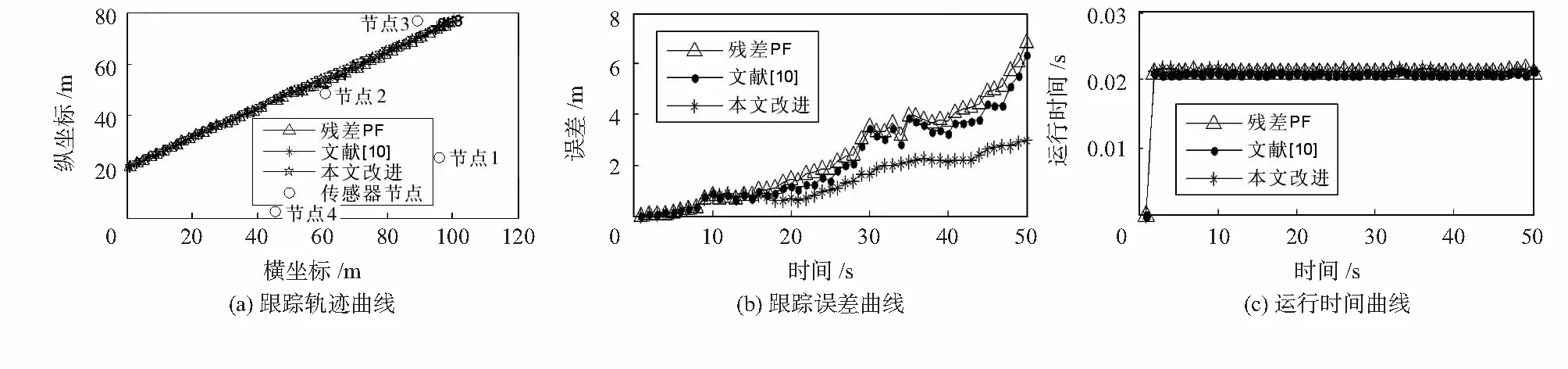
圖1 目標勻速直線運動曲線Fig 1 Curves of uniform motion of target in a straightline

圖2(a)是目標轉彎運動時三種算法跟蹤軌跡曲線，在40 s之后除本文改進算法外的其他兩種算法估計狀態偏離真實狀態。圖2(b)是目標轉彎運動時三種算法跟蹤誤差曲線，在50 s時文獻[10]中改進的殘差重采樣粒子濾波算法跟蹤誤差比殘差重采樣粒子濾波算法跟蹤誤差降低了3.8 %，本文改進算法跟蹤誤差比殘差重采樣粒子濾波算法跟蹤誤差降低了67.8 %。可見，跟蹤誤差是逐漸增大的，但本文改進算法跟蹤誤差是三種算法中增大的最慢的。圖2(c)是目標轉彎運動時三種算法運行時間曲線，可見三種算法的運行時間近似。

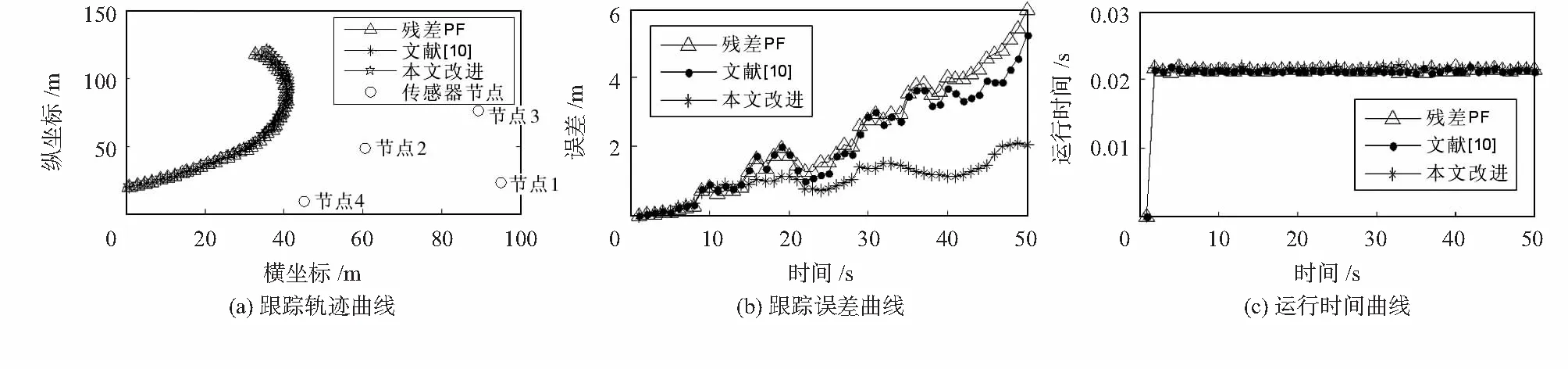
圖2 目標轉彎運動曲線Fig 2 Curves of target motion of turning

表1是三種粒子濾波算法的平均跟蹤誤差，從表中可見，殘差重采樣粒子濾波算法的誤差值最大，文獻[10]改進的殘差重采樣粒子濾波算法的誤差值次之，本文改進算法誤差最小。在直線運動時，本文改進算法跟蹤誤差比文獻[10]改進的殘差重采樣粒子濾波算法的誤差減少0.250 7m，比殘差重采樣粒子濾波算法的誤差減少了1.052 8m。在轉彎運動時，本文改進算法跟蹤誤差比文獻[10]改進的殘差重采樣粒子濾波算法的誤差減少0.206 3m，比殘差重采樣粒子濾波算法的誤差的減少了1.254 3m。可以看出，改進重采樣粒子濾波與文獻[10]改進的殘差重采樣粒子濾波算法和殘差重采樣粒子濾波算法相比，目標跟蹤精度得到提高。重采樣實質消除權值小的粒子，復制權值大的粒子，多次迭代后會造成粒子枯竭現象，從上述仿真中可以看出，本文改進的算法跟蹤誤差在三種算法中最小，由此可以說明，在算法中產生新的粒子，增加粒子的多樣性，可以提高跟蹤精度。

4 結束語

粒子濾波存在退化現象，采用重采樣后存在粒子枯竭

表1 不同粒子濾波算法的平均跟蹤誤差Tab 1 Average tracking error of different PF algorithms

現象。對此，本文提出了一種基于改進重采樣的粒子濾波無線傳感器網絡目標跟蹤算法。該算法在重采樣的過程中，產生新的粒子，增加粒子的多樣性，另外該算法避免了殘差重采樣中殘留粒子重采樣問題。仿真結果表明，該算法提高了跟蹤精度。

[1] Hamouda Y E M,Phillips C.Adaptive sampling for energy-efficient collaborative multi-target tracking in wireless sensor networks[J].IET Wireless Sensor Systems,2011,1(1):15-25.

[2] Zhao Y,Chen W,Gao J.Advances in mechanical and electronic engineering [M].Berlin/Heidelberg:Springer,2012:387-391.

[3] 谷 靜,史健芳.分布式粒子濾波算法在目標跟蹤中的應用[J].傳感器與微系統,2014,33(8):158-160.

[4] Arulampalam M S,Maskell S,Gordon N,et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tra-cking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188.

[5] 劉 剛,彭 力.權值選優粒子濾波的無線傳感器網絡目標跟蹤[J].傳感器與微系統,2011,30(6):30-32.

[6] 席志紅,付存利.基于 MCMC 的改進粒子濾波算法[J].計算機工程與設計,2014,5(9):3070-3074.

[7] 國 輝,敬忠良,胡洪濤.基于優化組合重采樣的粒子濾波算法[J].上海交通大學學報,2006,40(7):135-139.

[8] 常天慶,李 勇,劉忠仁,等.一種改進重采樣的粒子濾波算法[J].計算機應用研究,2013,30(3):748-750.

[9] 馮 馳,王 萌,汲清波.粒子濾波器重采樣算法的分析與比較[J].系統仿真學報,2009,21(4):1101-1105.

[10] 馮 馳,趙 娜,王 萌.一種改進殘差重采樣算法的研究[J].哈爾濱工程大學學報,2010,31(1):120-124.

[11] 黃小平,王 巖,陳冰潔.基于粒子濾波的分布式目標跟蹤算法[J].計算機工程,2011,37(4):84-86.

Target tracking algorithm for WSNs based on improved particle filtering*

DING Ting-ting, GAO Mei-feng

(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi 214122,China)

Aiming at particle impoverishment phenomenon caused by particle filtering resampling,a target tracking algorithm for WSNs based on improved resampling particle filtering is presented for the WSNs.The proposed algorithm avoids residual particle resampling problem,thus reduces calculation time;by producing new particles,diversity of particles is increased,so particle impoverishment phenomenon is improved.Simulation experimental results show that the improved resampling particle filtering algorithm improves target tracking precision and reduce tracking error.

target tracking; wireless sensor networks(WSNs); particle filtering(PF); resampling; particle impoverishment

10.13873/J.1000—9787(2016)07—0140—03

2015—10—12

國家自然科學基金資助項目(61373126)

TP 393

A

1000—9787(2016)07—0140—03

丁婷婷(1990-)，女，安徽安慶人，碩士研究生，主要研究方向為檢測技術與自動化裝置。