中考題中的直角三角形

蔡金鳳

?

中考題中的直角三角形

蔡金鳳

直角三角形是中考必考的重要內容之一，在填空、選擇、解答題中都有可能出現，在解答題中它往往與三角函數、相似三角形等相結合.本文以直角三角形為載體，剖析中考中是如何在考查基礎知識的同時又考查分類討論思想的.

一、有關邊的分類

例1（2014·涼山）已知一個直角三角形的兩邊的長分別是3和4，則第三邊長為_______.

【分析】此題易受勾三股四弦五的影響，填一個答案5.其實應看4充當什么邊，因此要分：①4是斜邊，②4是直角邊，可根據勾股定理求出上述兩種情況下第三邊的長.

解：①當4是斜邊時：

②當4是直角邊時：

二、有關角的分類

例2（2015·江西）如圖1，AB=BC= 4，AO=BO，P是射線CO上的一個動點，∠AOC=60°，則當△PAB為直角三角形時AP的長為_______.

【分析】分三種情況討論：1.以∠APB為直角有兩種情況，點P在線段CO上，或點P在CO的延長線上；2.以∠ABP為直角.

解：①如圖2，∠APB=90°，

∵AO=BO，∠APB=90°，

∴PO=AO=BO=2，∠AOC=60°，

∴△APO是等邊三角形，∴AP=2.

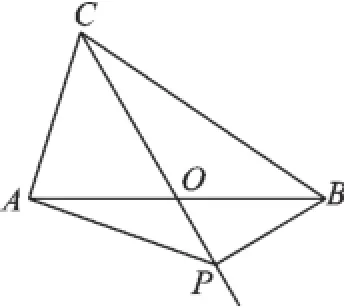
圖1

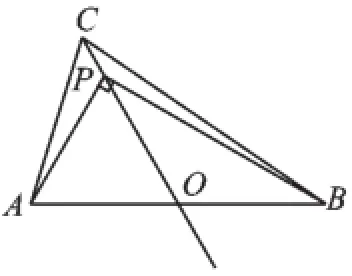
圖2

②如圖3，∠APB=90°，

∵AO=BO，∠APB=90°，

∴PO=AO=BO=2，

又∠AOC=60°，∴∠BAP=30°，

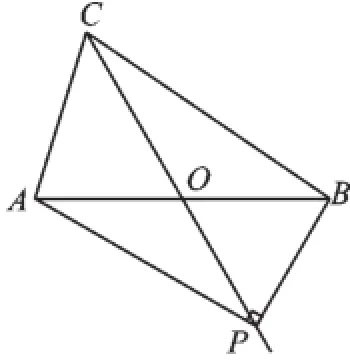
圖3

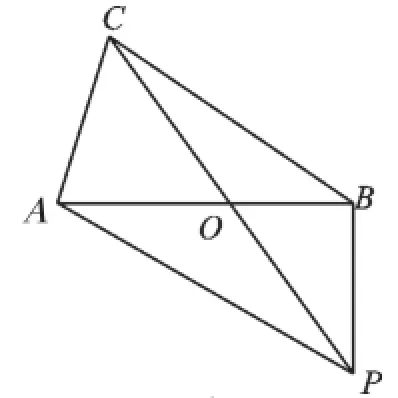
圖4

③如圖4，∠ABP=90°，

∵BO=AO=2，∠BOP=∠AOC=60°，

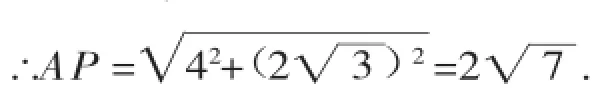
例3（2015·聊城，有刪減）如圖5，在直角坐標系中，Rt△OAB的直角頂點A在x軸上，OA=4，AB=3.動點M從點A出發，以每秒1個單位長度的速度，沿AO向終點O移動；同時點N從點O出發，以每秒1.25個單位長度的速度，沿OB向終點B移動.當兩個動點運動了x秒（0＜x＜4）時，解答下列問題：

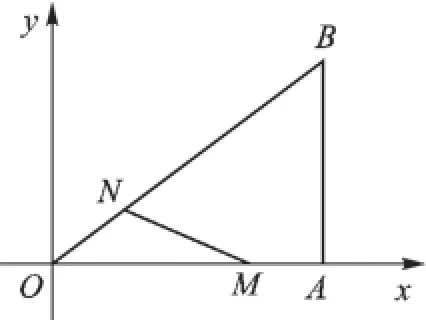
圖5

（1）（2）略.

（3）在兩個動點運動過程中，是否存在某一時刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，請說明理由.

【分析】在△OMN中，有一個角是確定的，就是∠MON，另外兩個角是變化的.∠ONM由鈍角逐漸變成銳角，它肯定在某一個時刻是90°，∠OMN由銳角逐漸變成鈍角，它也存在著某一個時刻是90°，因此此題存在著兩種情況：

①若∠OMN=90°，則MN∥AB，由平行線得出△OMN∽△OAB，得出比例式，即可求出x的值；

②若∠ONM=90°，則∠ONM=∠OAB，證出△OMN∽△OBA，得出比例式，求出x的值即可.

解：（1）（2）略.

（3）存在某一時刻，使△OMN是直角三角形，理由如下，分兩種情況：

①若∠OMN=90°，如圖6所示，則MN∥AB，此時OM=4-x，ON=1.25x，

∵MN∥AB，∴△OMN∽△OAB，

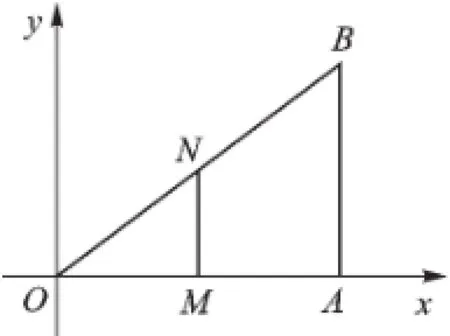
圖6

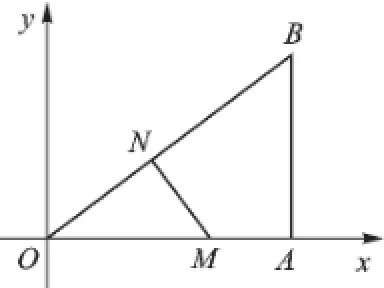
圖7

②若∠ONM=90°，如圖7所示，

則∠ONM=∠OAB，此時OM=4-x，ON= 1.25x，

∵∠ONM=∠OAB，∠MON=∠BOA，

∴△OMN∽△OBA，

同學們，解題有時之所以要分類討論，是由于某些元素的不確定性，或說某些元素的多種可能性.例1中4可能是斜邊也可能是直角邊；例2中P點可能在OC上，也可能在OC延長線上，從而導致直角也有兩種可能；例3中動點M、N都有可能是直角頂點.所以要想順利解題，首先要認真審題，弄清圖形產生的過程，確定不確定元素有哪些可能性，在直角三角形這一塊，有關邊，要分清哪條是直角邊，哪條是斜邊，有關角要分清哪個角是直角.

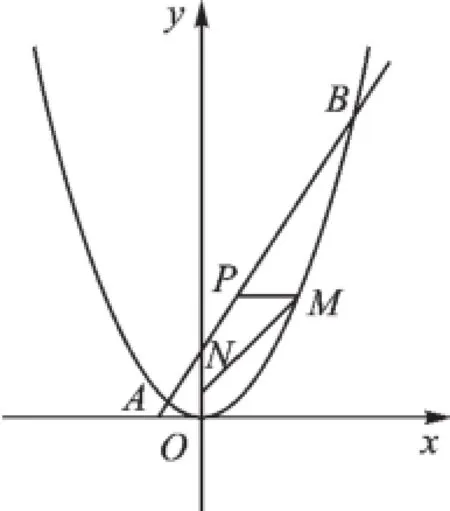
圖8

小試身手

（1）求這條直線的函數關系式及點B的坐標.

（2）在x軸上是否存在點C，使得△ABC是直角三角形？若存在，求出點C的坐標，若不存在，請說明理由.

（3）過線段AB上一點P，作PM∥x軸，交拋物線于點M，點M在第一象限，點N（0，1），當點M的橫坐標為何值時，MN+3MP的長度最大？最大值是多少？

【提示】（1）首先求得點A的坐標，然后利用待定系數法確定直線的解析式，從而求得直線與拋物線的交點坐標.

（2）過點B作BG∥x軸，過點A作AG∥y軸，交點為G，然后分三種情況：

①若∠BAC=90°，則AB2+AC2=BC2；

②若∠ACB=90°，則AB2=AC2+BC2；

③若∠ABC=90°，則AB2+BC2=AC2.

（3）略.

2.在平面直角坐標系中，點A，B的坐標分別為（-3，0），（3，0），點P在反比例函數y=足條件的點P的個數為（）.

A.2個B.4個C.5個D.6個

【提示】分∠PAB=90°，∠APB=90°，∠PBA=90°三種情況求點P的個數：

①當∠PAB=90°時，則P點的橫坐標為-3，由反比例函數圖像上點的坐標特征容易得到P點有1個；

③當∠PBA=90°時，P點的橫坐標為3，此時P點有1個.

（作者單位：江蘇省鹽城市明達中學）