基于相容性的區間直覺模糊信息的逆判問題
陳 巖,金 爽,楊依寧
(沈陽工業大學 理學院,沈陽 110870)
群組決策需要利用各專家給出的判斷矩陣計算綜合排序向量,若專家意見分歧較大時勉強進行集結,其結果往往難以具有說服力。如何衡量判斷矩陣之間的差距,多大的差距可以容許,都可以用相容性予以表征。Saaty[1]針對群決策問題提出了相容性檢驗的概念,許多學者針對各類判斷矩陣的相容性問題開展了大量的研究工作。對于確定性信息判斷矩陣的相容性研究,學者們已經提出了較為成熟的相容性指標和相容性檢驗方法[1-2]。對于不確定性信息判斷矩陣的相容性問題,徐澤水[3]針對區間模糊偏好信息判斷矩陣給出其相容性定義及其性質。陳華友等[4]對不確定加性語言偏好信息判斷矩陣的相容性及其在群組決策中的應用進行了研究。在此基礎上,徐澤水[5]又針對基于直覺模糊偏好信息判斷矩陣以及區間直覺模糊偏好信息判斷矩陣的相容性進行研究,并給出了基于滿意相容性調整其判斷矩陣一致性的方法。Jiang等[6]對直覺乘性偏好信息的相容性問題進行了研究,并給出2個一致性調整的優化模型。
在眾多的群決策問題中,如何有效解決專家之間意見的一致性與沖突性,將個人意見綜合為可反映專家群體的一致性意見,以及從一致性的角度分析評判每個專家的判斷水平(即逆判問題),是群決策研究的重要問題。劉萬里[7]采用統計分析法,給出AHP 判斷矩陣的逆判問題的方法。陳巖等[8]通過將互補判斷矩陣和語言判斷矩陣轉化為互反判斷矩陣,通過數理統計分析法解決群決策中互補判斷矩陣的逆判問題;陳俠等[9]利用相對偏差給出了互補判斷矩陣的評判方法;鞏在武等[10]利用相關度給出了直覺模糊判斷矩陣的逆判方法;夏梅梅等[11]在此基礎上,通過相似度給出了區間直覺模糊判斷矩陣的逆判方法。本文首先從區間直覺模糊數的相容性概念出發,根據其性質給出區間直覺模糊判斷矩陣的一個相容性指標,以及衡量區間直覺模糊判斷矩陣相容性的準則。然后對區間直覺模糊信息進行了一致性分析,進一步得出了基于相容性的區間直覺模糊判斷矩陣的逆判方法。最后,通過算例驗證了此方法的可行性和有效性。
1 基本概念和定義
定義1[14]設X是一個非空集合,
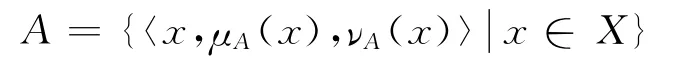
為直覺模糊集,其中,μA(x)、νA(x)分別為元素x屬于集合X的隸屬度和非隸屬度,且滿足條件

1-μA(x)-νA(x)為X中元素x屬于X的猶豫度。
由于客觀事物的復雜性和不確定性,μA(x)和νA(x)的值難以用精確的數值表示,而用區間數形式表示比較實際,故對直覺模糊集[12-13]進行了拓展,稱

為區間直覺模糊集,其中,區間數μA(x)、νA(x)滿足

根據文獻14,區間直覺模糊集的基本組成部分是由元素x屬于X的區間隸屬度和區間非隸屬度所組成的有序區間對(本文稱為區間直覺模糊數)。為方便起見,將區間直覺模糊數的一般形式簡記為([a,b],[c,d]),其中,

定義2[14]若m=([al,au],[bl,bu]),其中,

則稱m為一個區間直覺模糊數。
定義3[14]若m=([al,au],[bl,bu])為一個區間直覺模糊數,稱mc=([bl,bu],[al,au])為m的補數。且稱區間直覺模糊數m與m c互補。
2 區間直覺模糊數的相容性
定義4設區間直覺模糊數

為m、n的相容度。
c(m,n)有下列性質:
(1)0≤c(m,n)≤1。
(2)自反性,即c(m,m)=0。
(3)對稱性,即c(m,n)=c(n,m)。
證明
(1)因為

所以c(m,n)≥0,當al=1時,au=1,這時,bl=bu=0,即m=([1,1],[0,0]),要使c(m,n)取最大值,則n=([0,0],[0,0]),c(m,n)取最大值為1;同理,當

時,均使c(m,n)=1為最大值,即0≤c(m,n)≤1。
(2)、(3)易得,證明從略。
定理1對于區間直覺模糊數,具有互補一致性,即c(m,n)=c(mc,nc)。
證明根據定義3,有:

根據定義4,有:

設區間直覺模糊數m0=([al,au],[bl,bu]),簡記 為m0=(a,b),其中,a=[al,au],b=[bl,bu]。則a左移i個單位,b左移j個單位,得區間直覺模糊數

a右移i個單位,b右移j個單位,則得區間直覺模糊數

同理可得區間直覺模糊數

定理2對于區間直覺模糊數,具有平移一致性,即

證明根據定義4,有:

3 區間直覺模糊判斷矩陣的相容性
定義5[15]設 判斷矩陣A=[mij]n×n,其 中,mij=(μij,νij),i,j=1,2,…,n,為區間直覺模 糊數,滿足條件:
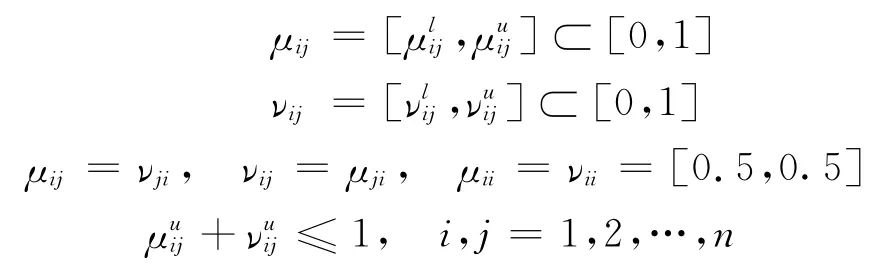
則稱A為區間直覺模糊判斷矩陣。
定義6設A=[mij]n×n,B=[nij]n×n,為區間直覺模糊判斷矩陣,其中:

為區間直覺模糊判斷矩陣A、B的相容度,c(mij,nij)由定義4求得。
定義7設A=[mij]n×n,B=[nij]n×n,為區間直覺模糊判斷矩陣,其中:

稱A、B是完全相容的,若?i,j∈N,均有mij=nij,即A=B。
由相容性性質(1)和定義6、7,易得如下定理:
定理3設A=[mij]n×n,B=[nij]n×n,為區間直覺模糊判斷矩陣,則
(1)0 ≤C(A,B)≤n2,當A、B完全相容時,C(A,B)=0。
(2)自反性,即C(A,A)=0。
(3)對稱性,即C(A,B)=C(B,A)。
證明從略。
定義8設A=[mij]n×n,B=[nij]n×n,為區間直覺模糊判斷矩陣,其中:

指標
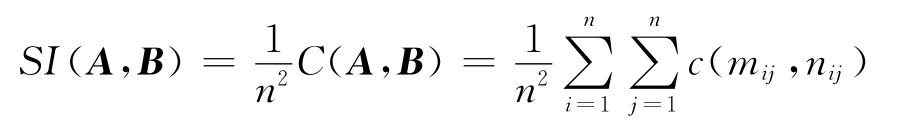
稱為區間直覺模糊判斷矩陣A、B的相容性指標。
由定理3可得,0≤SI(A,B)≤1,則A、B完全相容時,它們的相容性指標SI(A,B)=0。
定義9設A=[mij]n×n,B=[nij]n×n,為區間直覺模糊判斷矩陣,若,則稱A、B基本相容,其中為相容性指標的臨界值。S.I.根據實際情況而定,一般取。
定義10設,k=1,2,…,m,均為區間直覺模糊判斷矩陣,,ωi≥0,稱為區間綜合判斷矩陣。
定理4由區間直覺模糊判斷矩陣

集結的區間綜合判斷矩陣

也為區間直覺模糊判斷矩陣。
證明對于區間直覺模糊判斷矩陣


同理,易得

同理,易得:

定理5若,k=1,2,…,m,B=[nij]n×n,均為區間直覺模糊判斷矩陣,如果SI(A(k),B)≤,則對于區間綜合判斷矩陣,k=1,2,…,m也有。
證明由SI(A(k),B),根據定義8,有

又因為

所以

應用Cauchy-Schwarz不等式,上式可改寫為

4 區間直覺模糊判斷矩陣的一致性分析
定義11[16]設直覺模糊判斷矩陣

其中,rij=(μij,νij),若滿足

則稱矩陣R為加性一致性直覺模糊判斷矩陣。
由于μij=νji,νij=μji,故可得如下推論:
推論1設直覺模糊判斷矩陣R=[rij]n×n,其中,rij=(μij,νij),若滿足

則稱矩陣R為加性一致性直覺模糊判斷矩陣。
考慮直覺模糊判斷矩陣加性一致性滿足的條件和性質,現給出區間直覺模糊判斷矩陣加性一致性的定義。
定義12設區間直覺模糊判斷矩陣


則稱矩陣A為加性一致性區間直覺模糊判斷矩陣。
由于

故可得如下推論:
推論2設區間直覺模糊判斷矩陣


則稱矩陣A為加性一致性區間直覺模糊判斷矩陣。
定理6令s(ml)=al-bl,s(mu)=au-bu,如果

為加性一致性區間直覺模糊判斷矩陣,當且僅當

時成立。
證明必要性。由
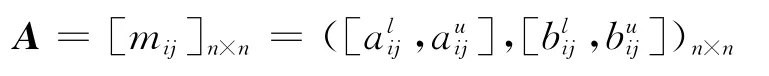
為一致性區間直覺模糊判斷矩陣,根據式(3),得:

因為

則上式可改寫為:

且s(ml)=al-bl,s(mu)=au-bu,則:

上面的證明逆推即為充分性,證明從略。
5 基于相容性的逆判方法
根據前面的討論,可以獲得一組加性一致性區間直覺模糊判斷矩陣
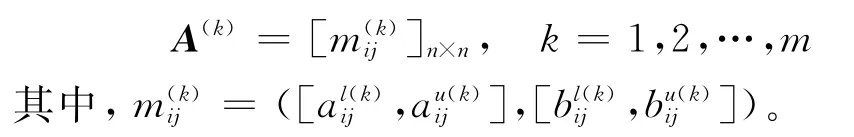
根據定理4和定義12,易得如下定理:
定理7由加性一致性區間直覺模糊判斷矩陣,k=1,2,…,m,集結的區間綜合判斷矩陣

也為加性一致性區間直覺模糊判斷矩陣。
證明從略。

根據相容度的性質,將相容性指標作為專家評判的標準,SI(A(k))表示專家所做出決策與集體決策的貼近程度,相容性指標越小,則專家決策越接近集體決策,專家評判的水平越高。
根據前面的討論,基于相容性的區間直覺模糊判斷矩陣逆判方法的過程如下:
(1)對于一個群決策問題,決策者ek(k=1,2,…,m)對所有方案集進行比較,并構造區間直覺模糊判斷矩陣,滿足

(2)將所有區間直覺模糊判斷矩陣R(k)=,k=1,2,…,m轉化為加性一致性區間直接模糊判斷矩陣。
(4)計算每一個區間直覺模糊判斷矩陣R(k)和加性一致性區間綜合判斷矩陣的相容性指標。
6 算例分析
例 5個決策者ek(k=1,2,3,4,5)分別對5個方案x i(i=1,2,3,4,5)進行評估,且決策者的權重向量,得到5個區間直覺模糊判斷矩陣R(k)(k=1,2,3,4,5):

應用基于區間直覺模糊判斷矩陣逆判方法的步驟,可得:
(1)已獲得區間直覺模糊判斷矩陣R(1)、R(2)、R(3)、R(4)、R(5)。
(2)將所有區間直覺模糊判斷矩陣

轉化為加性一致性區間直接模糊判斷矩陣




(4)計算每一個區間直覺模糊判斷矩陣R(k)(k=1,2,3,4,5)和加性一致性區間綜合判斷矩陣的相容性指標(k=1,2,3,4,5),得:

(5)根據相容性指標的大小對專家進行排序。
因此,專家評判水平為e5?e3?e2?e1?e4。
7 結語
本文通過研究區間直覺模糊數的相容度性質,提出了區間直覺模糊判斷矩陣相容度及相容性指標的定義,進一步分析了區間直覺模糊判斷矩陣的加性一致性;通過專家給出的信息偏好,給出了基于相容性指標區間直覺模糊信息的逆判方法。有關區間直覺模糊信息的乘性一致性充分必要條件以及應用相容性進行一致性的調整方法可能是未來研究工作的方向。

