基于Ramp-型需求及混合指數分布變質率的變質性物品庫存系統的訂貨策略

趙連霞

（上海大學 管理學院，上海 200444）

在現代快速流轉的庫存管理中，對變質性物品（如水果、蔬菜、藥品、化學品以及電子產品等）的庫存控制問題越來越引起流通企業、經銷商的重視。這是因為，如果忽略了物品的變質或損耗將影響庫存成本，從而對企業的利潤產生重要影響，所以對于有關運營系統的庫存控制問題的研究就不可能忽略這些因素。從已有的文獻來看，變質性物品的庫存問題目前獲得了廣泛的研究。Whitin［1］最早對該問題進行了探討，他主要考慮了時尚商品在規定存儲期末的變質問題。Bakker等［2］對近年來變質性物品的庫存模型的發展趨勢作了完整的綜述。

Mandal等［3］、Wu等［4］和Manna等［5］研究了一類需求率為Ramp-型的變質性物品的庫存模型，此需求類型在新的消費品上市過程中最為常見，即需求率隨新消費品上市時間推移而增至某一固定點時達到穩定。Deng等［6］將文獻［3-4］中的研究條件擴展到庫存系統的起始為缺貨的情形。閔杰等［12］則通過考慮隨時間變化的短缺量拖后率對庫存訂貨策略的影響，建立了一類具有一般形式的短缺部分拖后的庫存補充模型。李衛元等［13］研究了允許缺貨情況下物品變質率服從威布爾分布的庫存模型。劉斌等［14］研究了缺貨損失高于補貨成本易逝品的供應鏈契約。孫靜春等［17］利用一類非線性成本庫存模型，建立了一個生產者-訂貨商兩級易逝品供應鏈運營模式，給出了供應鏈參與各方在無合作、合作及一體化3種模式下的易逝品生產訂貨模型。Cheng等［7-8］對具有類梯形需求模式的變質性物品庫存問題進行了研究。更多的相關文獻可參考文獻［9-11，15-16，18］。

上述文獻研究的庫存模型中所考慮的需求率僅為線性或分段線性需求的情形。在實際的庫存管理活動中，需求率并不都是線性的，而是在一定時期內可能是非線性增長的，在另一時期內則可能是市場需求飽和的穩定情況。同時，當庫存成本和變質成本高于短缺成本時，庫存短缺甚至是一種營銷策略。在庫存出現空缺期間，如果顧客愿意等待至下一次補貨時取得商品，廠商僅承擔缺貨損失，不喪失銷售機會；但有時部分顧客會轉向購買其他商家的產品，原來的生產商則會遇到撤單現象，由此產生機會損失成本。因此，研究物品在現貨銷售和預銷售條件下，允許短缺且部分拖后的庫存控制有更加現實的意義。

本文研究了Ramp-型需求條件下具有混合指數分布率的變質性物品的庫存模型。在假設需求率為分段函數形式下，分別就庫存系統起始條件為備貨銷售和缺貨預銷售的情形建立了相應的庫存模型，并且給出了模型的最優庫存安排策略；同時，通過數值算例給出了該庫存模型的最優安排策略的實現過程。

1 符號與假設

本文庫存模型的建立用到以下記號：

D（t）—有限計劃時期內的需求率，假設為Ramp-型，即

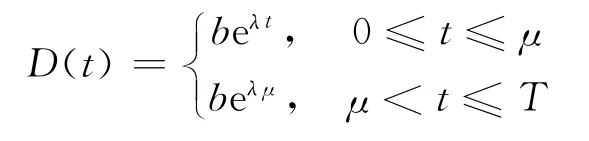
其中：μ為需求拐點；b為基本市場容量，為非負常數；λ∈（0，1）為常數。

I（t）— 時刻t的庫存量，0≤t≤T

T— 固定的訂貨周期，t1為在訂貨周期內存貨達到0的時刻，0＜t1＜T

物品開始變質的時間服從混合指數分布，物品的變質率

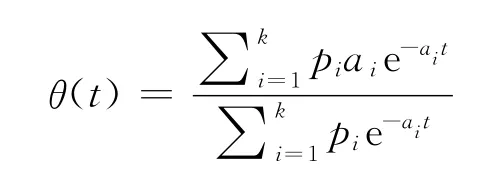
其中，

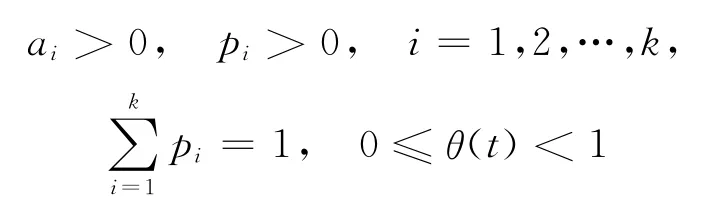
允許短缺但產生部分延后，延后率為e-δx，其中，x為顧客等待時間，δ為正常數

c1，c2，c3，c4—單位物品在單位時間內的庫存費用、變質損失費用、缺貨損失費用和撤單損失費用

S，Q—每個訂貨周期內最大庫存量和訂貨量

Ci（t1），（i=1，3）—0≤t1≤μ單位時間平均費用

Ci（t1），（i=2，4）—μ≤t1≤T單位時間平均費用

2 現貨銷售條件下的系統庫存模型及分析

根據符號及假設，可得本文所研究的庫存系統：系統在t=0時刻進貨，訂購批量為Q，在［0，t1］時段庫存量由于需求和物品本身的變質而下降，在t1時刻系統庫存量減少到0。由于經銷商訂貨需求的變化，在時段［t1，T］內發生缺貨且缺貨允許部分延后，故在［0，T］內的庫存水平可用下述微分方程描述：

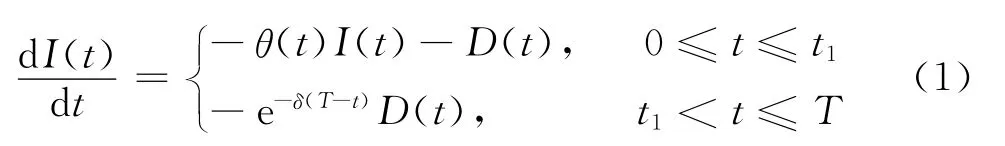
邊界條件I（t1）=0。

由于物品需求滿足Ramp-型，下面根據系統中庫存量為0時刻所處階段分為兩種情形：

情形1當t1≤μ時，方程式（1）可表示為

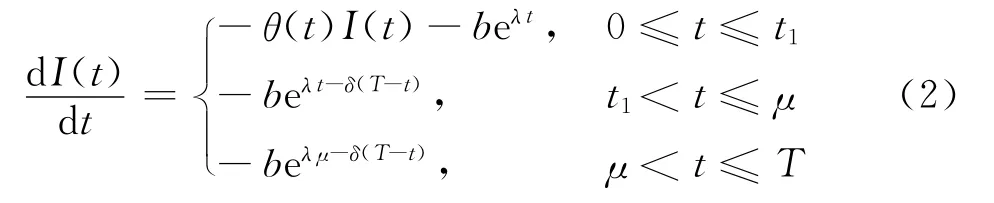
利用邊界條件I（t1）=0，解上述方程組，可得

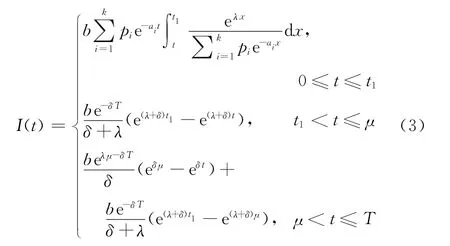
對于一個訂貨周期T，t=0時的庫存水平

在時段［0，t1］內的變質損失量

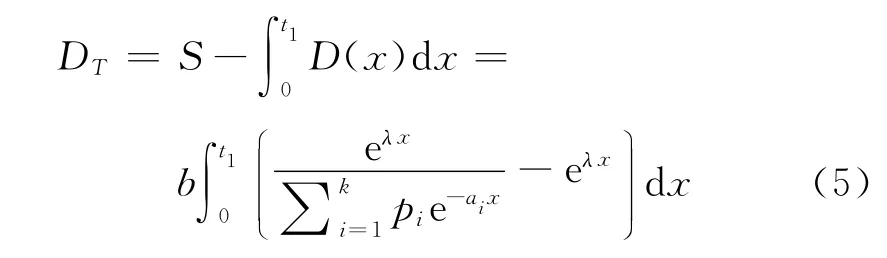
在時段［0，t1］內總的庫存量

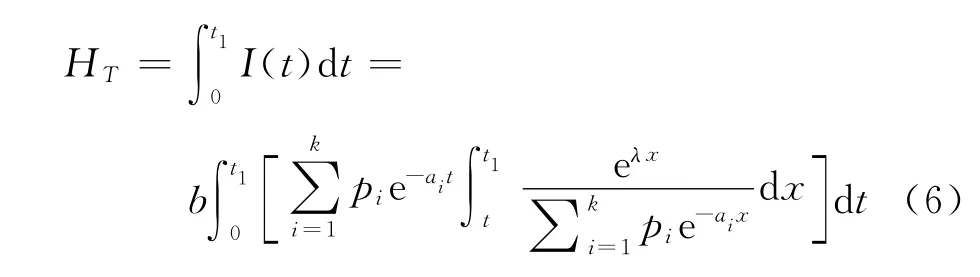
在時段［t1，T］內的缺貨總量

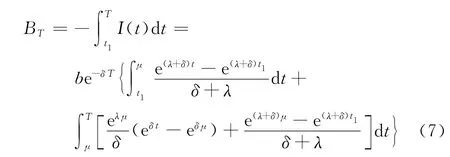
在時段［t1，T］內的失銷總量

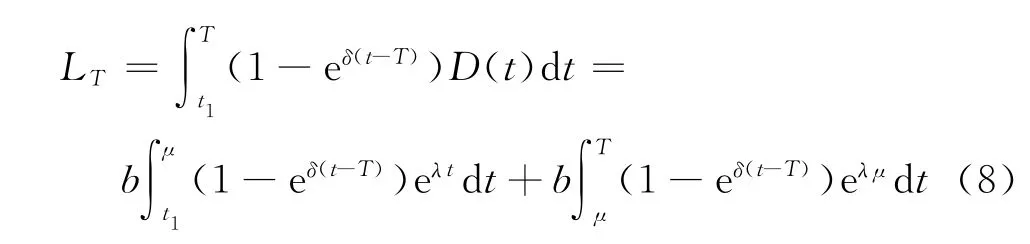
由式（5）～（8），即可得在條件t1≤μ≤T下，單位時間的平均費用為

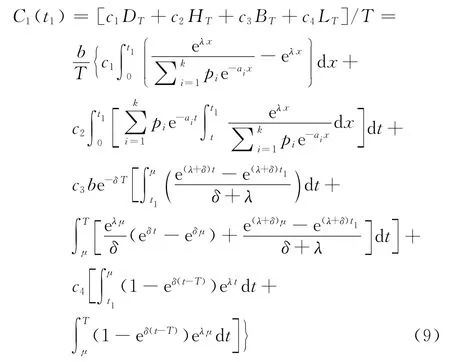
對C1（t1）分別求關于t1的導數，得

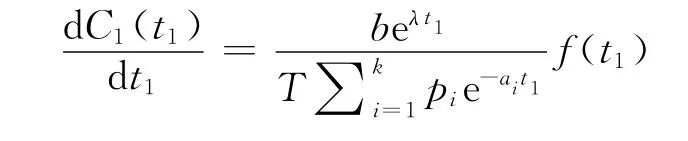
其中，

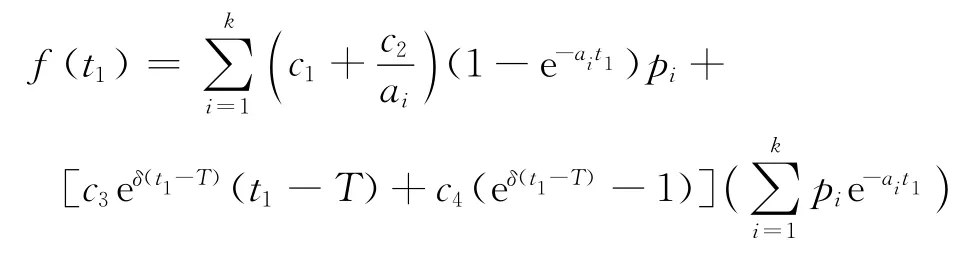
由

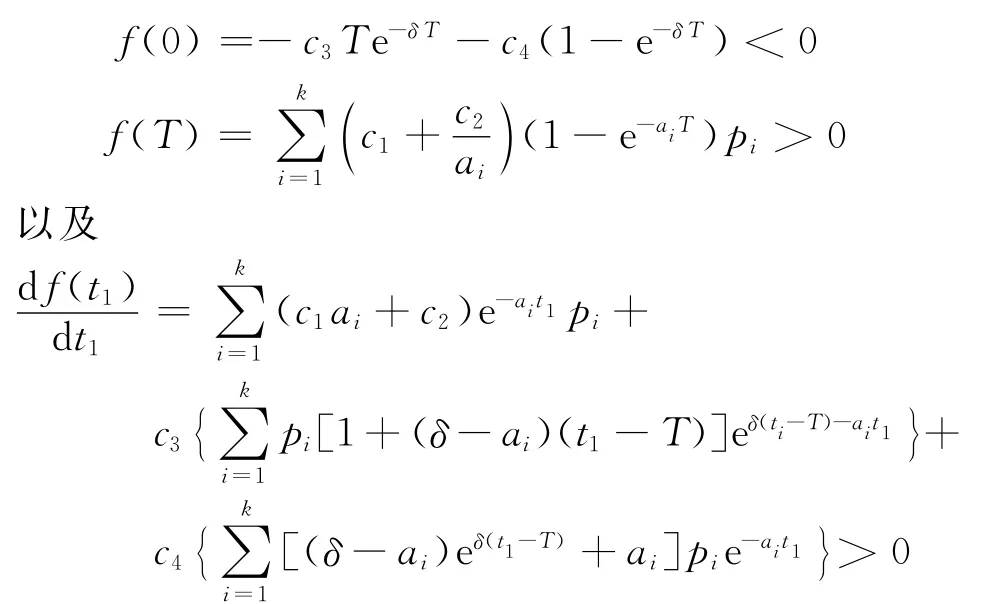
可得函數f（t1）存在唯一的零點，不妨設為，即為=0，又由于

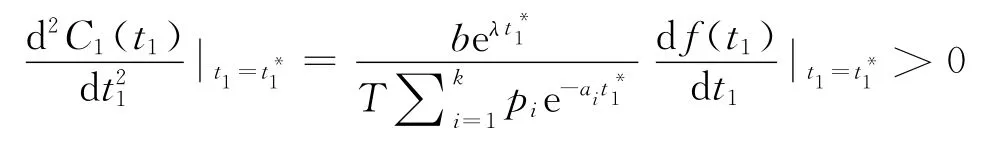
故可得：

引理1對于現貨銷售條件下的變質性物品庫存系統，當0≤t1≤μ時，若f（μ）＞0，則平均費用C1（t1）在∈（0，μ）獲得最小值；若f（μ）≤0，則平均費用C1（t1）在t1=μ獲得最小值。

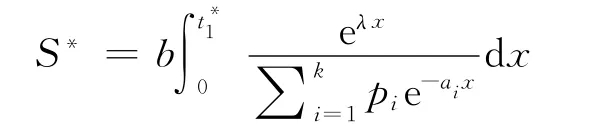
最佳訂貨量

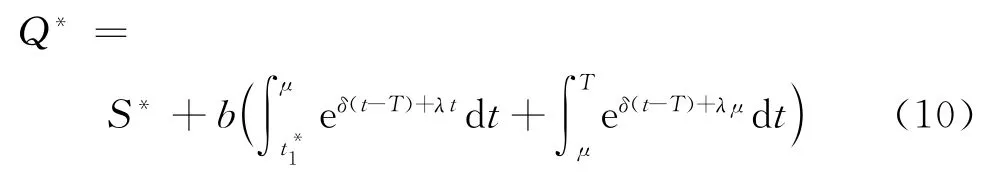
情形2當μ≤t1≤T時，方程式（1）為

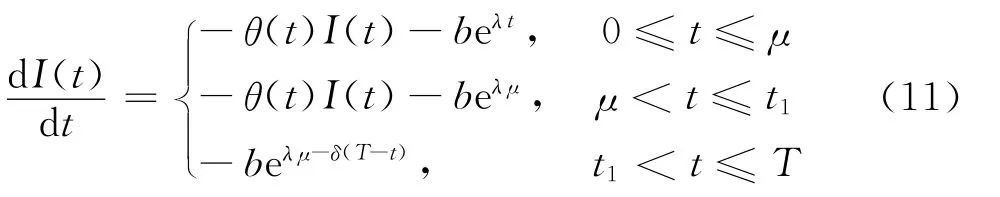
利用邊界條件I（t1）=0，解得

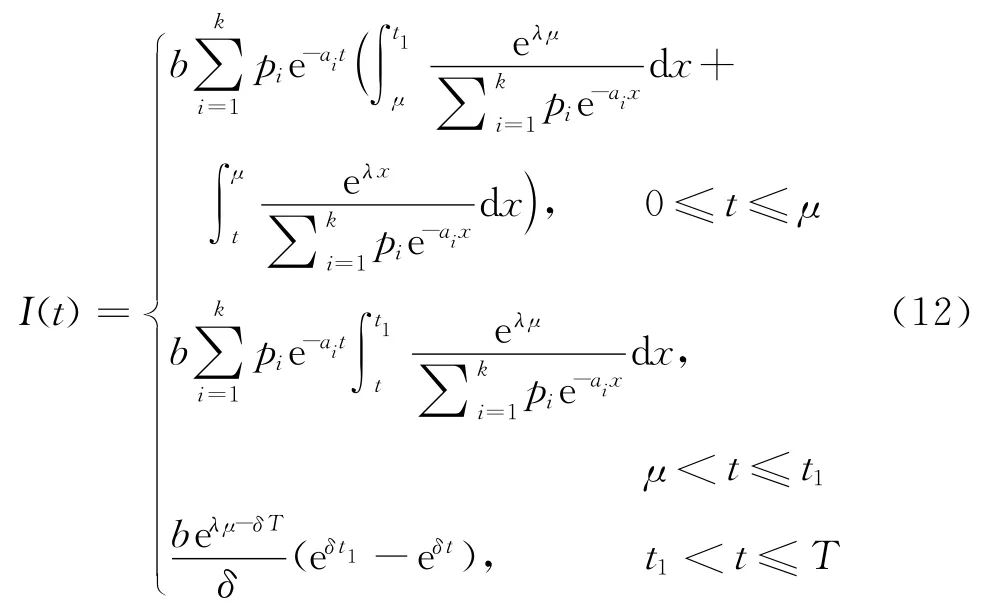
對于一個訂貨周期T，t=0時的庫存水平

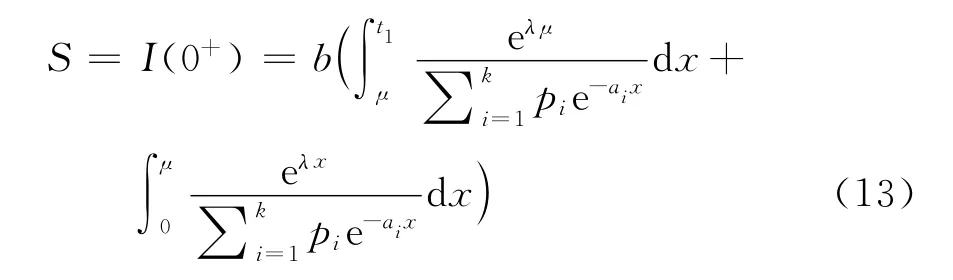
在時段［0，t1］內的變質損失

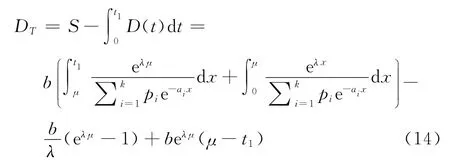
在時段［0，t1］內總的庫存量

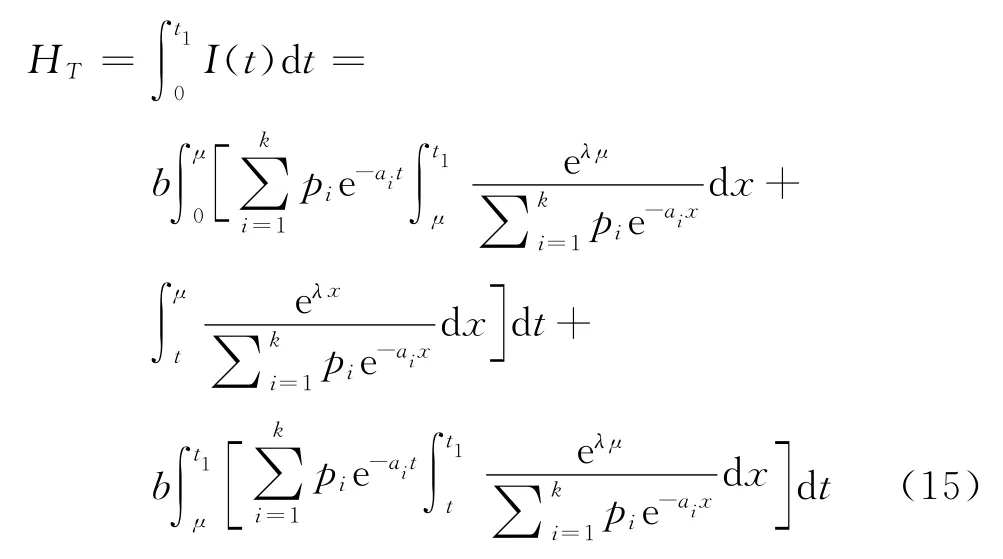
在時段［t1，T］內的缺貨總量

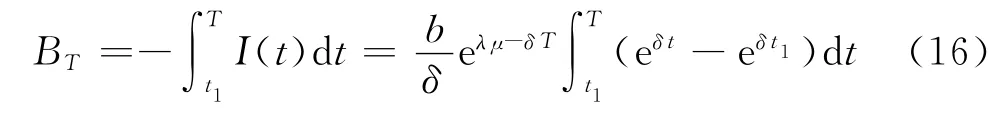
在時段［t1，T］內的失銷總量

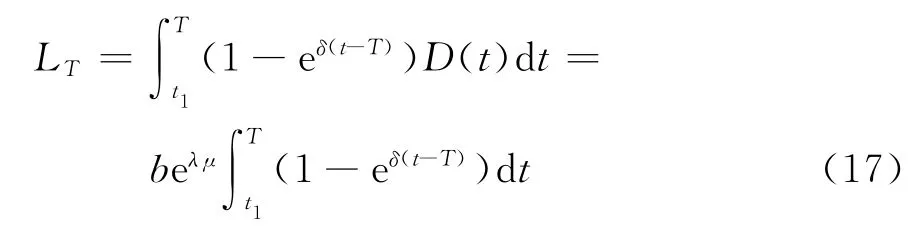
由式（14）～（17），可得在條件μ≤t1≤T下單位時間的平均費用為

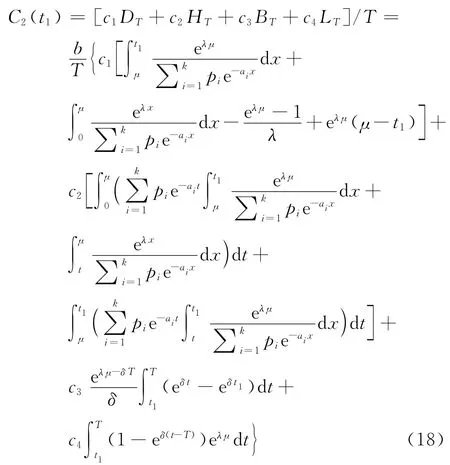
對C2（t1）求關于t2的導數，得

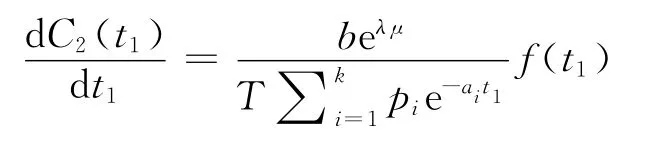
其中，

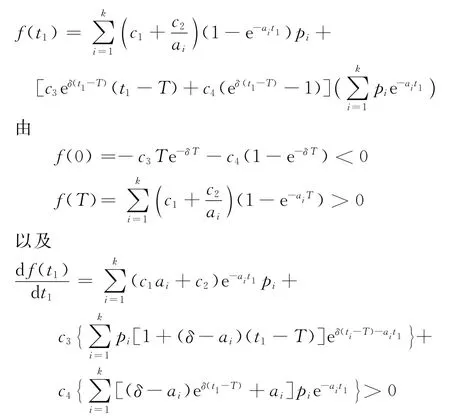
可得函數f（t1）存在唯一的零點，不妨設為，即為=0，又由于

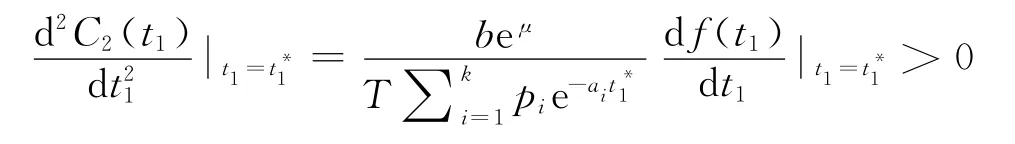
故可得：

引理2對于現貨銷售條件下的變質性物品庫存系統，當μ≤t1≤T時，若f（μ）＜0，則平均費用C2（t1）在t1=∈（μ，T）獲得最小值；若f（μ）≥0，則平均費用C2（t1）在t1=μ獲得最小值。

因此，當μ≤≤T時，則最佳庫存量

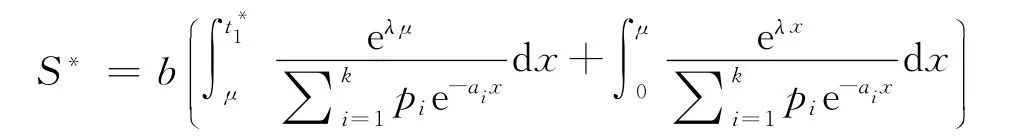
最佳訂貨量

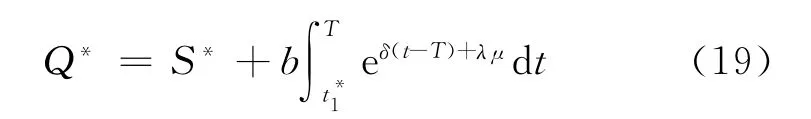
基于以上分析，可得［0，T］的現貨銷售條件下變質性物品庫存系統的平均費用為

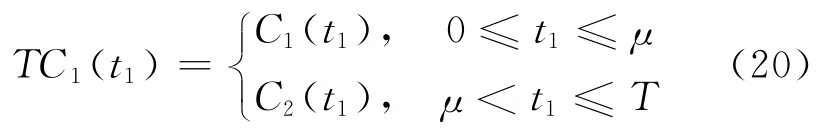
式中，C1（t1）和C2（t1）分別由式（9）、（18）確定。

綜合以上分析，可得在現貨銷售條件下，允許短缺且部分延后的變質性庫存系統的最優訂貨策略：

（1）輸入參數c1、c2、c3、c4、ai、p i、b、λ、μ、T。

（2）求解方程f（t1）=0，不妨設所得解為，若∈（0，μ］，則最佳訂貨量和最小費用分別由式（10）、（9）確定；若∈（μ，T］，則最佳訂貨量和最小費用分別由式（19）、（18）確定。

3 預銷售條件下的系統庫存模型及分析

本節討論系統起始為預銷售情形。根據符號及假設，庫存系統可描述為：庫存系統在t=0 時刻沒有庫存，因而經銷商不能及時給訂單客戶供貨，直到上游制造企業在時刻t1給經銷商補貨同時補足客戶訂單且庫存量達到最大S，訂購批量為Q，在［t1，T］時段庫存量由于進一步需求和庫存變質而下降，故在［0，T］內的庫存水平可用下述微分方程描述：

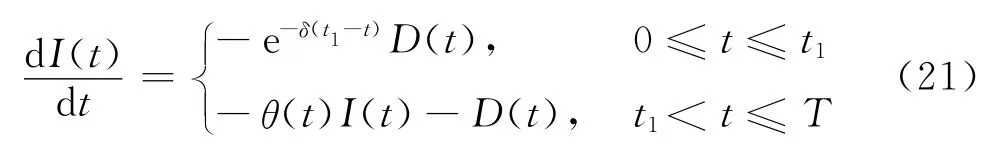
邊界條件I（0）=I（T）=0。

由于物品需求為Ramp-型分段需求模式，下面根據系統中庫存達到最大時刻所在階段分為兩種情況：

情形1當0≤t1≤μ時，方程式（21）為

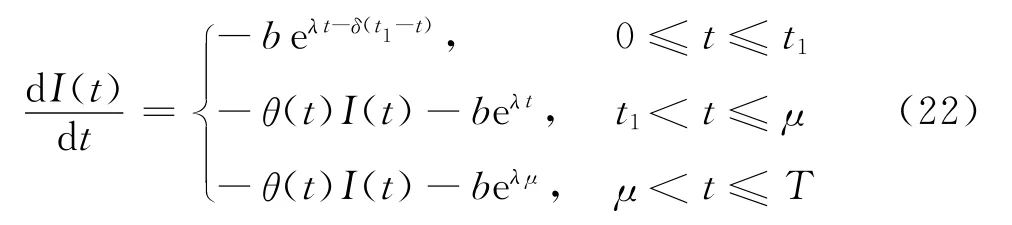
利用邊界條件I（0）=I（T）=0，解上述方程組，可得

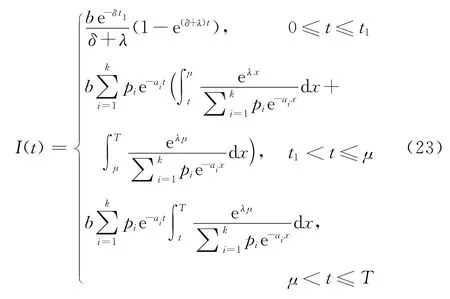
對于一個訂貨周期T，t=t1時的庫存水平

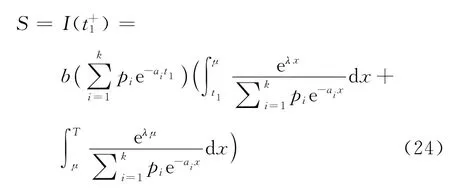
在時段［t1，T］內的變質損失

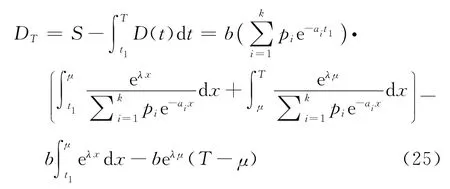
在時段［t1，T］內總的庫存量

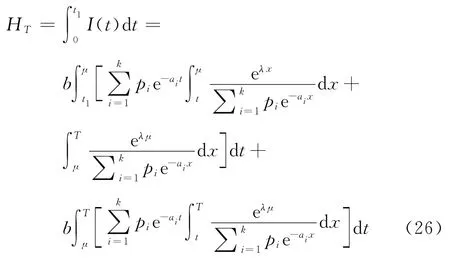
在時段［0，t1］內的短缺總量

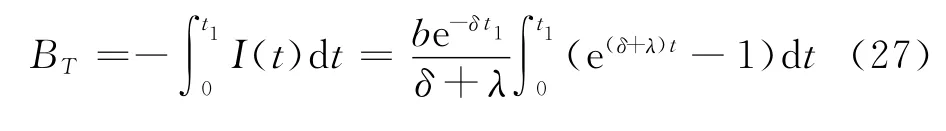
在時段［0，t1］內的撤單總量

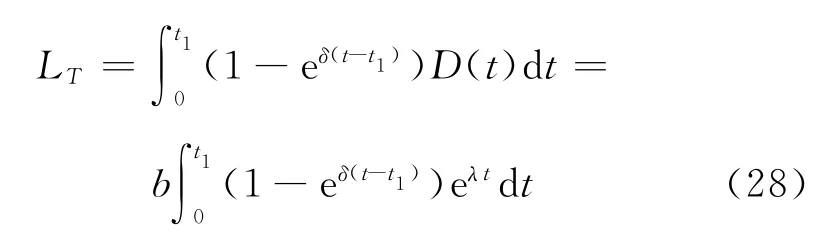
則在條件0 ≤t1≤μ下，單位時間的平均費用為

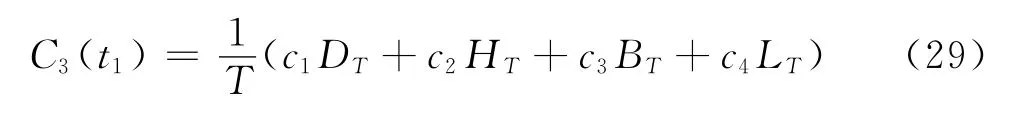
將式（25）～（28）代入式（29），并求關于t1的導數，可得

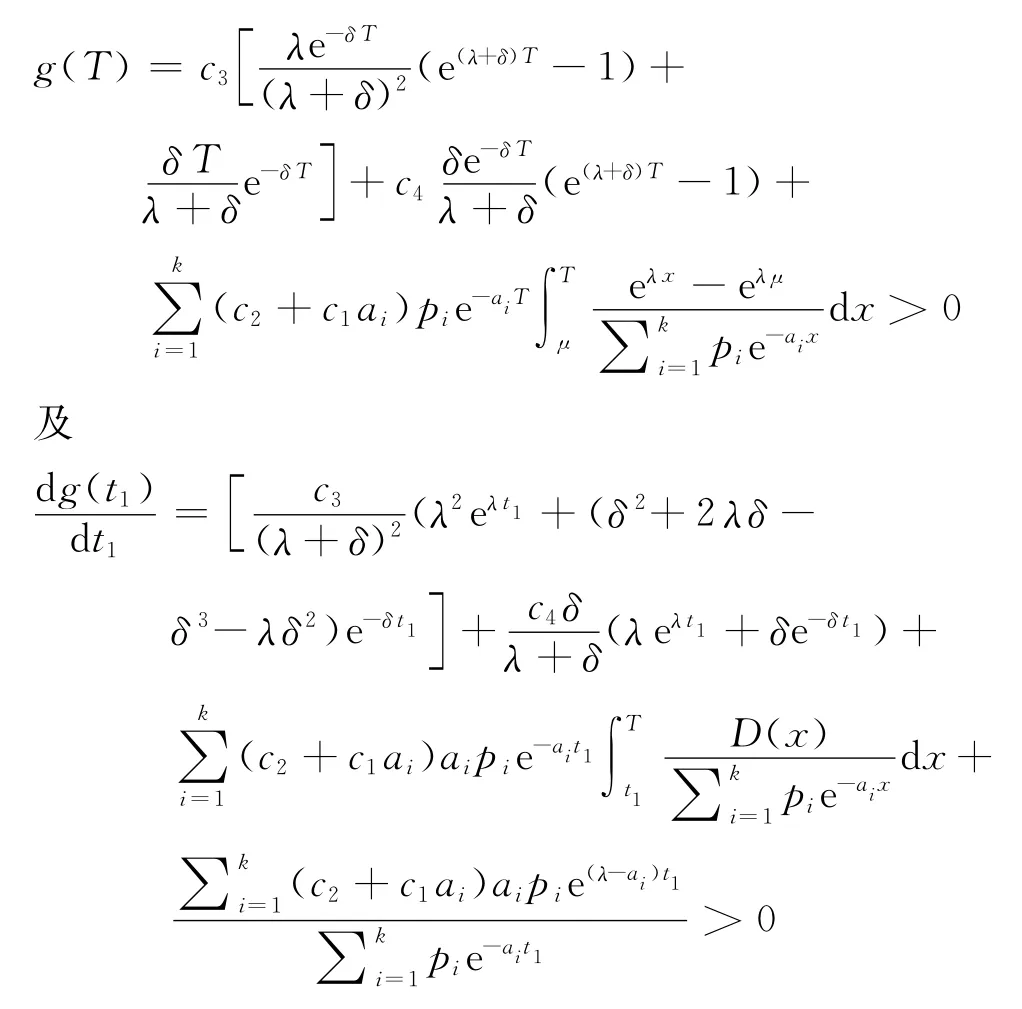
可得函數g（t1）存在唯一的零點，不妨設為，即為=0，因而有：

引理3對于預銷售條件下的變質性物品庫存系統，當0≤t1≤μ時，若g（μ）＞0，則C3（t1）在可獲得最小值，其中=0；否則，C3（t1）在t1=μ獲得最小值。

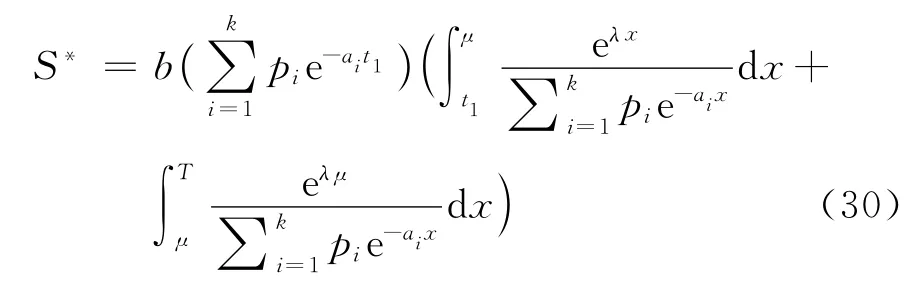
最佳訂貨量

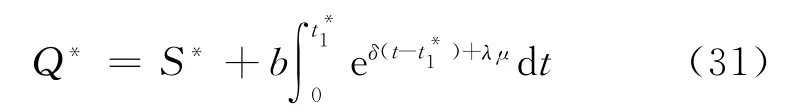
情形2當μ≤t1≤T時，方程式（21）為

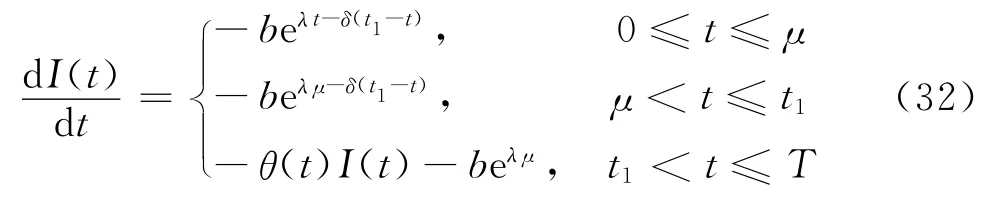
利用邊界條件μ≤t1≤T，解上述方程組，可得

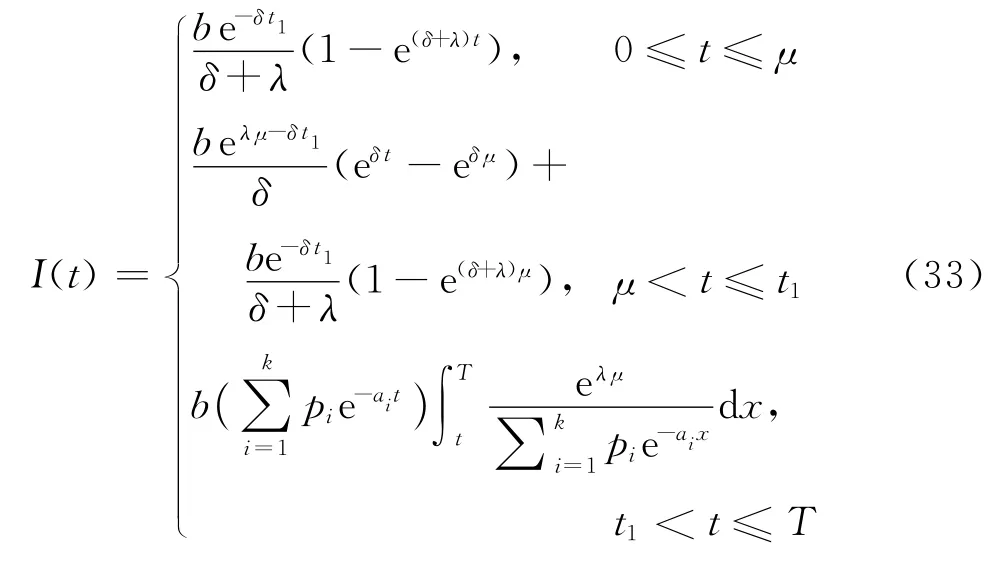
對于一個訂貨周期T，整個庫存系統的庫存水平

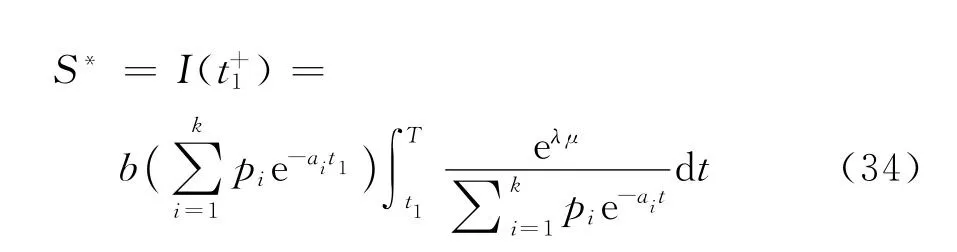
在時段［t1，T］內的變質損失

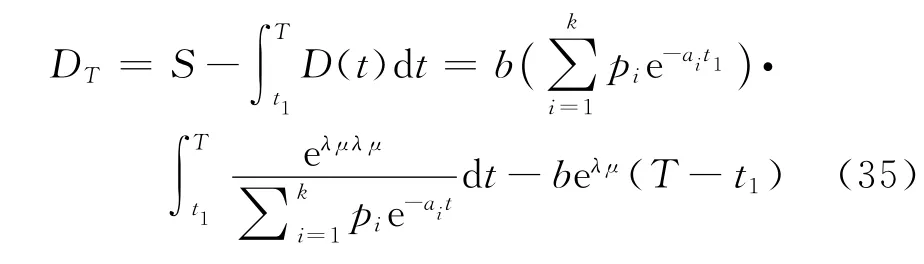
在時段［t1，T］內總的庫存量

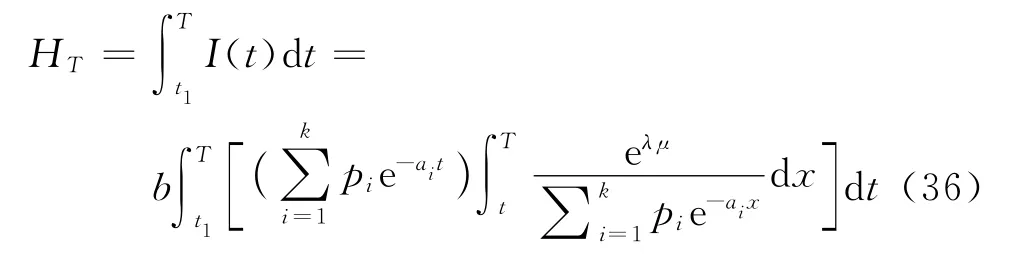
在時段［0，t1］內的缺貨總量

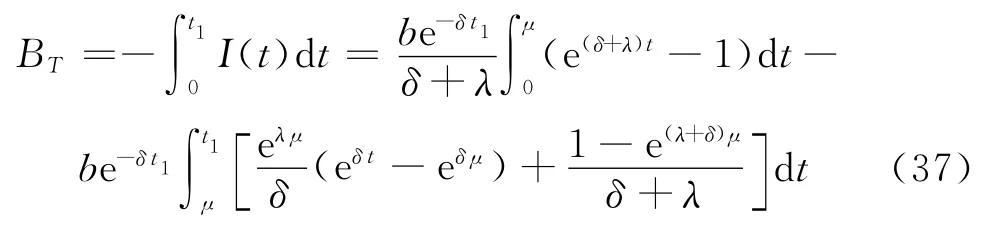
在時段［0，t1］內，由于缺貨而造成的撤單總量

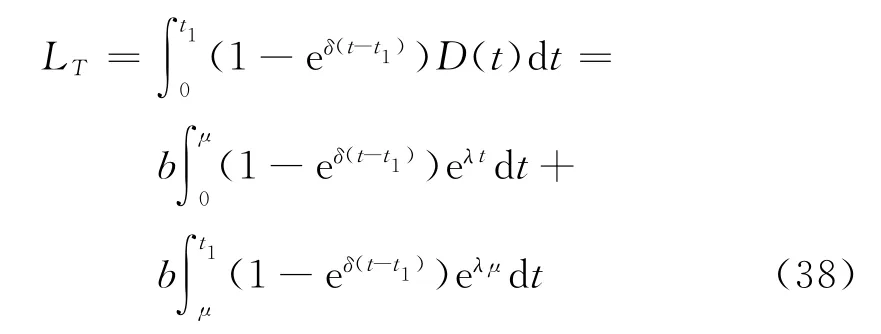
類似地，在條件μ≤t1≤T下，單位時間的平均費用為

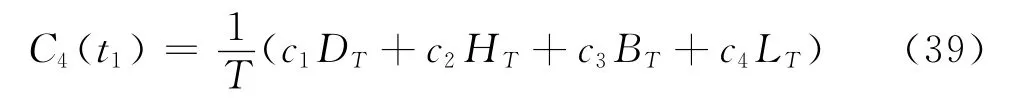
將式（35）～（38）代入式（39），并求關于t1的導數，即得

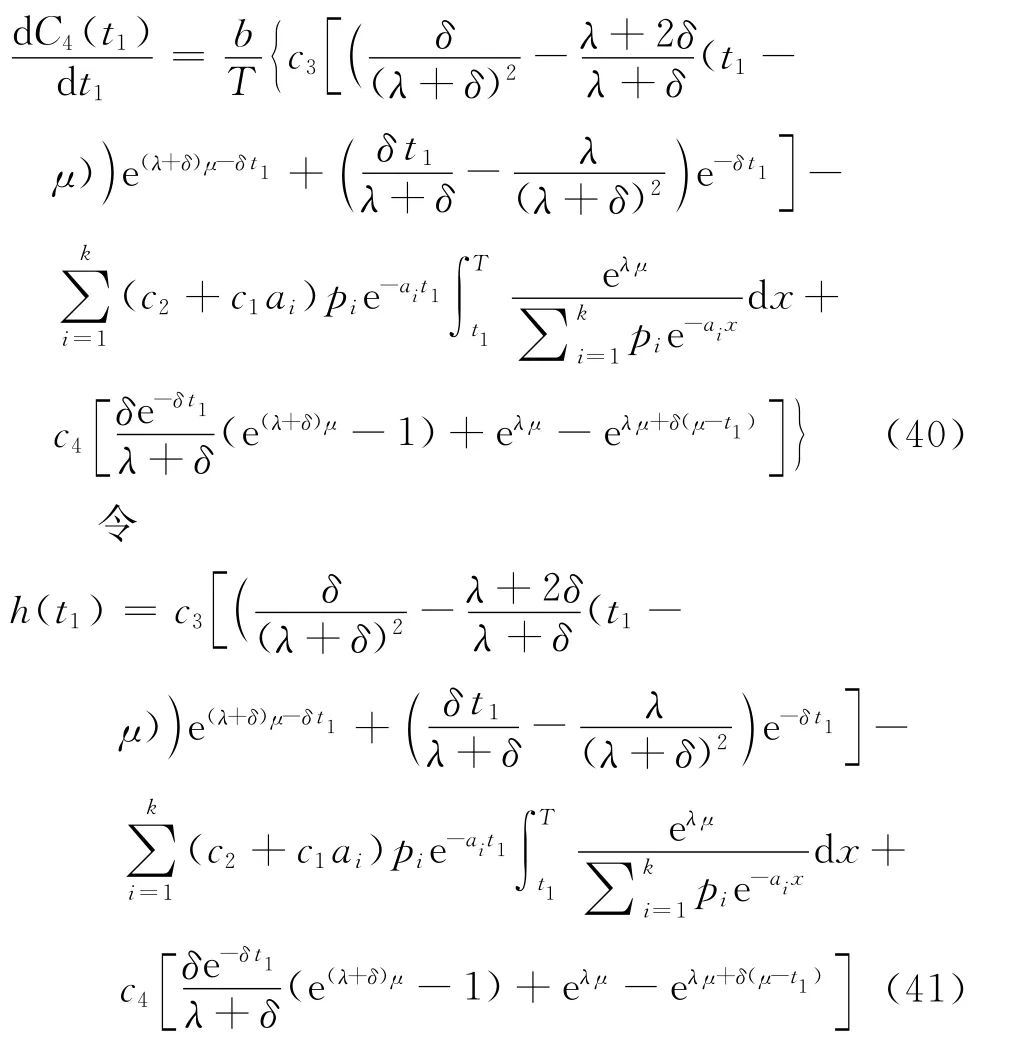
則有

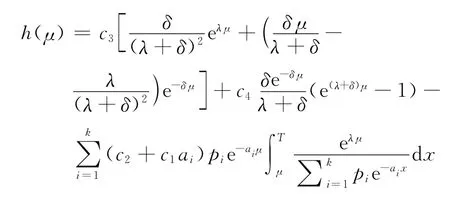
及

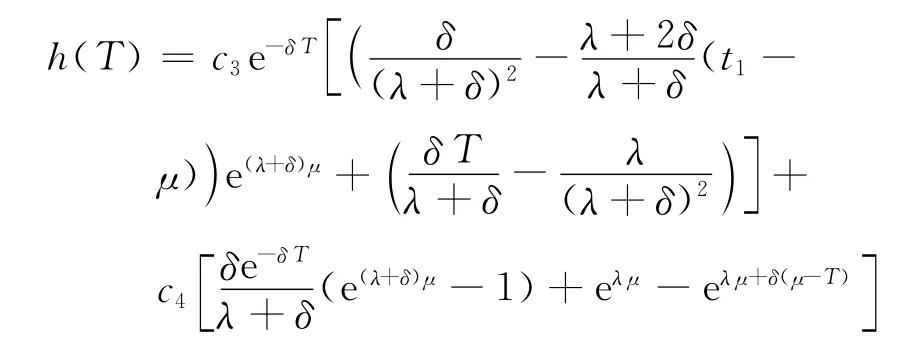
又由于

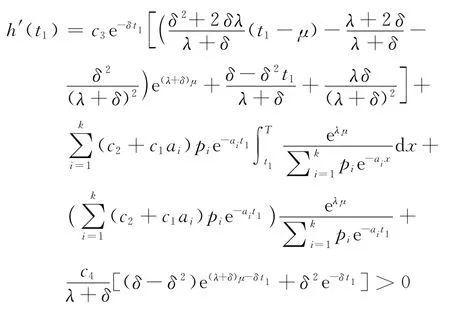
故h（t1）為一單調遞增函數，因而可得：

引理4對于預銷售條件下的變質性物品庫存系統，當μ≤t1≤T時，若h（μ）h（T）＜0，則C4（t1）在t1=可獲得最小值，其中=0；否則，C4（t1）在t1=μ獲得最小值。

因此，當μ≤≤T時，則最佳庫存量

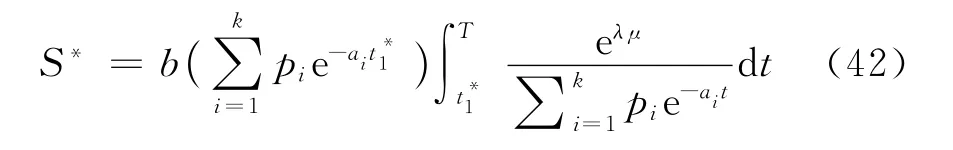
最佳訂貨量

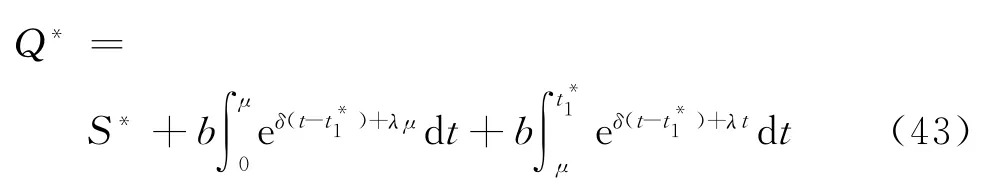
基于以上分析，可得［0，T］的預銷售條件下，變質性物品庫存系統的平均費用為

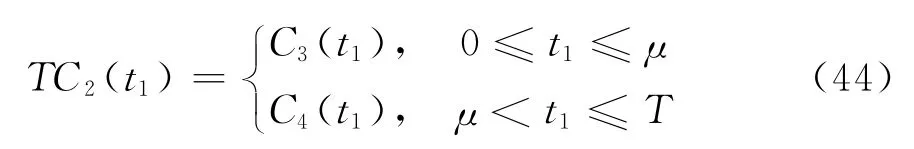
式中，C3（t1）和C4（t1）分別由式（29）和（39）確定。

綜合以上分析，可得預銷售條件下庫存系統的最優策略算法：

（1）輸入參數c1、c2、c3、c4、ai、p i、b、λ、μ、T。

（2）求解方程g（t1）=0，不妨設所得解為，若∈（0，μ］，則最佳訂貨量和最小費用分別由式（33）、（29）確定；否則=μ。

（3）求解方程h（t1）=0，不妨設所得解為，若∈（μ，T］，則最佳訂貨量和最小費用分別由（43）、（39）確定；否則，=μ。

4 數值實例及靈敏度分析

下面通過數值實例分析檢驗最優庫存策略的實施過程。

例1假設某裝配企業計劃在一個周期內（T=12）制訂某產品A 配件的訂貨計劃。單位配件每天的庫存保管費c1=5$，變質損失費用c2=10$，缺貨損失費用c3=12$，撤單損失費用c4=4$，需求函數

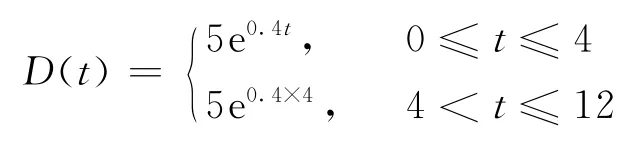
短缺延后率δ=0.2，變質率函數有關參數：

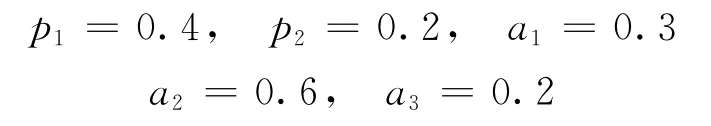
假設在現貨庫存系統體系下，利用Mathematica 9.0 軟件計算可得：最佳缺貨點=1.316，最佳訂貨量Q*=116.385，最小費用=278.394。

假設在預銷售庫存系統體系下，利用Mathematica 9.0 軟件計算可得：最佳補貨點=7.812，最佳訂貨量Q*=201.371，最小費用=571.836。

表1 參數λ對缺貨點、最佳訂貨量和費用的影響（現貨庫存系統）

表2 參數μ 對缺貨點、最佳訂貨量和費用的影響（現貨庫存系統）

表3 參數δ對缺貨點、最佳訂貨量和費用的影響（現貨庫存系統）

表4 參數λ對訂貨點、最佳訂貨量和費用的影響（預銷售庫存系統）

表5 參數μ 對訂貨點、最佳訂貨量和費用的影響（預銷售庫存系統）

表6 參數δ對訂貨點、最佳訂貨量和費用的影響（預銷售庫存系統）

5 結語

本文研究了Ramp-型需求條件下變質性物品的庫存系統最優策略模型。在假設需求率為有限容量的非線性函數形式下，分別就庫存系統起始條件為現貨銷售和預銷售情形下建立相應的庫存優化模型，并且給出了模型的最優庫存策略。同時，通過數值算例給出了該庫存模型的最優庫存策略的實現過程。結果表明，生產商提供現貨銷售或缺貨銷售情況下，庫存系統的相關參數（如需求參數λ，需求拐點參數μ，缺貨延遲參數δ）對經銷商的訂貨策略產生重要影響：當需求參數較大時，訂貨量將會增加，由此產生的庫存系統費用在現貨銷售情況下變化較為明顯；當缺貨延遲參數較大時，訂貨量明顯減少，由此產生的庫存系統費用在預銷售情況下變化較為明顯。因此對該類庫存問題深入研究能為庫存管理提供一些有益的啟示。