基于非對稱質量損失函數的分段參數設計

卓德保，胥京波，張 浙

（上海師范大學 商學院，上海 200234）

在產品（或系統）質量設計中，產品性能和質量取決于產品各質量參數的組合。當質量參數相互獨立時，各參數的最優即是產品整體性能和質量的最優；當質量參數間存在交互作用時，就要尋找各參數的最佳搭配關系，使得產品性能在此搭配關系下整體最優。參數設計是質量設計的重要內容，通過選擇產品（或系統）中所有參數值（包括原材料、零件、元件等）的最優搭配水平，使其對隨機因素的變化不敏感，從而抑制隨機因素對系統輸出質量的影響，達到系統輸出質量波動小，穩定性好，成本低的目的。質量損失函數是通過描述系統在不同參數值下的損失，來度量系統質量偏離目標值而引起的經濟損失。通常情況下，質量損失函數是圍繞目標值的對稱函數。但在實際中，損失函數并非一定是對稱的，如果在規定的容許范圍內，實際加工參數偏離目標值的方向不同，或偏離程度不同所造成的質量損失差別很大時，質量損失函數就會在目標值兩側形成非對稱性。在電子產品、化學過程、切削工具的磨損過程、許多形狀和位置誤差的設計等，常常存在非對稱現象。例如，在螺母的加工過程中，當實際加工的孔徑參數值小于規格下限時，產品會造成返工損失；而孔徑參數值大于規格上限時，會造成產品報廢損失。這兩種損失的不同，使得質量損失函數在目標值兩側是一邊較平坦，另一邊很陡峭，形成非對稱質量損失函數。在電子產品方面，質量特性值高于或低于目標值時，產品散熱、零件承受能力等因素會引發電子產品電阻等零件的變化，進而影響產品性能，使目標值兩側損失不同。如在熱敏電阻產品中，電流等質量特性值高于目標值時產品產熱過多，電阻變化較大，產品損失較大甚至失去功能；而質量特性值低于目標值時產品產熱較少，電阻的溫度變化較小，電阻變化不明顯，產品損失相對較少，造成目標值兩側損失不對稱的情況。

在這種情況下，采用對稱質量損失函數的方法進行參數設計已經不合適，需要尋找一種非對稱損失函數的度量方法，以便更精確的進行參數設計［1］。

實際研究中，許多學者在非對稱質量損失函數和參數設計方面進行了研究，并取得了一定成果。非對稱質量損失函數方面，陳本晶［2］提出了通過細分非對稱質量損失函數的區間，分段求取各個小區間上的質量損失值的方法來解決非對稱且不規則的質量損失函數的計算方法，這種方法為不規則的質量損失函數尋找到了解決方法，但其計算過程比較復雜，條件限制較多，且在2個端點質量損失值的確定上存在一定的不準確性；陳湘來等［3］在非對稱損失函數的質量特性值優化選擇中對不同情況下的質量損失進行分類討論，并列舉了特性指標值在規格界限內和界限外以及產品檢驗時3種情況的損失，并用MATLAB進行迭代計算，簡化了計算難度；余慧敏［4］對一類非對稱損失函數進行了最優不變估計，采用現有的非對稱函數模型和單調變換群對質量損失進行計算，能精確計算非對稱質量損失的值，但此種方法的局限性較大，只能適用于小部分數據。

在非對稱損失函數的計算方面，研究最多的是用期望的方法求解。程巖等［5-6］基于非對稱損失函數的參數設計中為2個質量損失系數建立損失系數比，將非對稱質量損失函數的2個公式整合為1個，建立起一個非對稱的質量損失函數式，而后通過求導的方式找到最優的參數，調整質量損失函數的目標值，進而減少產品損失，在非對稱損失下威布爾分布的參數設計中用威布爾分布方程，討論了在位置參數、尺度參數和形狀參數3個參數的情況下，利用期望求質量損失的值；胡家喜等［7］在非對稱損失函數正態分布總體的參數設計中考慮非對稱質量損失函數，分別用一次和二次函數進行計算，而后用期望的方法進行參數設計；張曉勤［8］在n維非對稱損失函數的參數設計中將非對稱損失函數擴展到n維，討論了在n維非對稱的質量損失函數下，調整參數設計的可行性，求出質量損失的最小解，并以此進行了相關的參數設計；張斌等［9］在基于截尾正態分布的最優過程均值的確定中，討論了在不對稱田口質量損失函數下截尾正態分布的最優過程均值的確定問題，通過靈敏度分析，研究了過程參數對過程均值選擇的影響。但非對稱損失函數的期望的方法實際上是將非對稱的質量損失函數做了一次對稱化的變化，將兩邊的特性值做了一次折中處理，形成一個具有一定近似性質函數模型，這種方法能夠非常方便地模擬出質量損失的值，但是獲得的數據實際上是一個估計值，并不是一個具體的數值，故準確性偏小；其次，利用期望值進行參數設計時，只是調整了目標值，對產品特性值的均值的波動沒有進行討論，忽略了靈敏性設計時均值的不穩定性；最后，利用期望進行計算時，僅僅考慮了在機械元件中產品的特性值圍繞目標值進行波動的情況，而對于電子元件中部分產品的特性值并不圍繞目標值波動，需要進行產品特性值的遷移。

在非對稱參數設計的研究中，許多學者提出了不同的方法，Wen等［10］討論了過程受控但不滿足規格限時過程均值的優化設計問題，Teeravaraprug等［11］提出運用回歸分析的方法確定最優過程均值；Chen等［12］在質量特性分別服從正態、對數正態和指數分布的情況下，討論了單邊規格限的最優均值的確定問題；Lee等［13］討論了基于田口對稱損失函數的過程方差優化模型。

本文利用對質量損失函數分段的方法，解決非對稱損失函數的參數設計問題。首先以目標值為分界點將非對稱數據分為2個區間，假設每個區間的數據分別對應2個不同正態分布的一半，由此構造這2個不同的對稱質量損失函數，再根據不同區間對應的質量損失函數進行參數設計。

1 非對稱質量損失函數的構造

1.1 非對稱質量損失函數的描述

質量損失函數的非對稱性是由于過程輸出參數落在目標值的上方和下方造成的質量損失率不同而形成的。故非對稱質量損失函數都可用圖1刻畫。

圖1 非對稱質量損失

圖1中的m為目標值，假定質量特性值落在目標值上時，質量損失為0。可將圖1分為2個區間：x≤m和x＞m，x≤m區間的損失函數可假定為對稱損失函數L1的左半部分，x＞m區間的損失函數可假定為對稱損失函數L2的右半部分，如圖2 所示。將L1左半部分與L2的右半部分組合即可得到非對稱方程的損失函數。

圖2 非對稱質量損失的處理分析

1.2 基于正態方法的非對稱質量損失度量

在正態假設中，田口［14］認為產品的質量損失可以用質量損失函數來計算，通過泰勒展開，并假設質量目標值上損失為0的前提下，得出二次質量損失函數的計算公式，即

式中：L（x）為產品質量損失；k為質量損失系數；x為質量特性值；m為目標值，通過泰勒公式的變形，不難得出，其中，A0為輸出質量特性為某一特定點時的質量損失值，Δ0為特定點的輸出質量特性值偏離目標值的大小［14］。

而質量損失函數的期望值［15］為

由式（2）可見，產品質量損失由兩部分構成：

（1）σ2=E（x-μ）2，由質量特性值圍繞均值的波動造成的損失，可通過減少標準差來增加產品的穩定性，即穩健性設計。

根據圖2 的處理方法，構造非對稱質量損失函數

對于非對稱損失函數，傳統方法是將2個函數用1個損失系數進行整合，形成一個統一的公式，即令r=k2/k1，將其稱為損失系數比［15］。則有

對于正態分布的曲線，其質量損失為

本文通過分段的方法進行質量損失的計算，通過分段質量損失加總的方法得到。其左側及右側的質量損失為：

同時，將產品特性值分組，特性值小于m時用L1（x）計算損失，特性值大于m時用L2（x）計算損失，而后再將2個損失加和就是總的損失值，即

2 非對稱情況下的分段參數設計方法

在分段質量損失計算的基礎上，本文用分段計算的方法進行參數設計：

在L1（x）=k1（x-m）2的情況下進行參數設計，構造L1（x）=k1（x-m）2的方程保留其左側并虛擬出方程對稱的另一半曲線，將L1（x）=k1（x-m）2的定義域擴展到x∈（-∞，+∞），方程L1（x）=k1（x-m）2成為一個完整的二次曲線，L1（x）關于m對稱。

此時，質量特性值x服從均值為μ，標準差為σ的正態分布，其密度函數為

此時存在兩種情況：

（1）當均值μ和目標值m重合時，產品的質量特性主要來自質量特性圍繞均值的波動（本文稱為第1類波動），此時，質量參數的設計主要采用減小此類波動的穩健性設計方法進行。

（2）當均值μ和目標值m不重合時，產品的質量損失一方面來自質量特性值均值偏離目標值的波動（本文稱為第2 類波動），另一方面來自質量特性值圍繞均值的波動（第1 類波動），質量參數的設計分兩步進行：①采用與第1 種情況相同的穩健性設計方法，減小質量特性圍繞均值的波動；②進行靈敏性設計，減小均值偏離目標值的波動。第2種情況存在均值左偏離目標值和均值右偏離目標值兩種可能，如圖3、4所示，此時需要尋找總體質量損失最小的均值點，并根據兩種可能判斷調整方向和大小。

圖3 均值向左偏離目標值

圖4 均值向右偏離目標值

同理，運用相同方法進行L2（x）=k2（x-m）2的設計。本文對第2種情況進行設計。在進行參數設計時，判斷產品的質量損失都來自于哪些方面的波動，如果兩種波動都存在并造成損失，則需要通過穩健性和靈敏性設計減少兩種質量損失。

2.1 穩健性設計

在穩健性設計的過程中，通過正交試驗尋找質量參數的最優組合，以使輸出質量特性值的波動最小。通過對每組參數組合的輸出質量特性值進行信噪比計算，確定信噪比最大的參數組合為穩健設計中的最優參數組合。其信噪比計算公式為

為了驗證最優參數設計的合理性，需要對各組參數組合進行質量損失測算。將產品的特性值根據目標值分為目標值左側的產品特性值以及目標值右側的產品特性值兩部分。對兩側的產品特性值分別計算質量損失，并將每個參數組合左右兩側的質量損失進行加和，如表1所示。求出總的質量損失之后，按照質量損失從小到大的順序排列參數組合方案。總質量損失最小時對應的參數組合為穩健性設計中的最優參數組合設計。可以驗證，在不存在第2類波動的情況下，質量損失最小的參數組合與信噪比最大的參數組合是一致的。

表1 產品特性值的損失計算圖表

當存在第2類波動時，質量損失是最小的參數組合與信噪比最大的參數組合可能不一致。

2.2 靈敏性設計

在靈敏性設計中，首先是在穩健性設計的基礎上利用環境因子，此處為噪聲因子，測定在不同的外界條件下參數組合的敏感程度以及質量特性值均值的調整量δ。調整不同的噪聲因子，并進行重復試驗，輸出不同噪聲因子條件下質量特性值的均值。在此基礎上，通過實驗設計判斷均值的穩定性，減少第2類波動造成的質量損失，而后計算總的質量損失，選擇總質量損失最小的參數設計為最佳方案。

在非對稱質量損失條件下，質量損失最小的均值μ未必就是設計目標值m。在調整輸出質量特性均值的過程中，需要確定均值調整目標值μ*及調整方向和大小。

（1）均值調整目標值μ*的確定。根據質量損失的計算公式：

對其關于期望值進行求導，得

做變換λ=（m-μ）/σ，并稱λ為調整參數。將其代入上式，可得

由式（13）可知，求解L（μ，σ2）的最小值，即求解?L（μ，σ2）/?μ=0時λ的值，分析可知，?L（μ，σ2）/?μ=0的解只與r有關，設質量損失L最小時λ的值為λ*，在質量特性波動最小的σ*下，使質量損失L（μ，σ2）最小的質量特性均值調整目標值為μ*，則滿足：

基于以上分析，需要找到損失系數比r與參數λ的函數關系，通過給出不同的r的值，計算?L（μ，σ2）/?μ=0，并計算對應參數λ的值。本文運用牛頓迭代法，得到r與λ的對應值，如表2所示。在實際應用中可通過查表直接引用。通過使用Matlab，可得r和λ的關系圖，如圖5所示。

表2 正態分布下最優調整參數表（r為損失系數比，λ為最優調整參數）

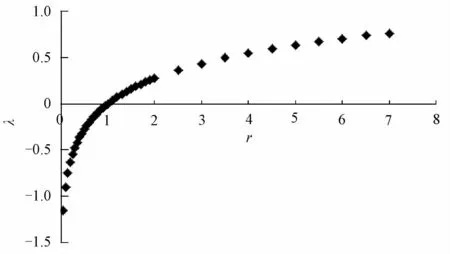
圖5 r和λ 的關系

由此可知，如果非對稱質量損失函數確定，則質量特性最佳均值調整目標值μ*（第2類波動帶來的質量損失最小）就確定了。在非對稱質量損失函數下，最佳均值調整目標μ*不等于目標值m，如圖6所示。

確定最佳均值調整目標值μ*后，需要討論在不同的外界環境下參數組合均值的波動問題。

對每種參數組合進行不同噪聲因子條件下的試驗，并多次重復，得到每種參數組合輸出質量特性的均值μ，計算各組參數組合下不同噪聲因子均值的均值和均值的方差，如表3所示。

其中，A、B、C、D 為相應的參數組合方案，μij為第i次重復試驗下第j個參數組合輸出質量特性的均值，為第j組參數組合的方差。

圖6 最佳均值的確定

表3 多組試驗參數組合的均值

（2）均值調整量Δ和調整方向的確定。當均值的均值與調整目標值μ*不重合時，可通過一定的技術手段找到與μ*的關系，確定調整量Δ的大小和方向，使均值的均值與均值調整目標值μ*重合。根據表3的計算結果。調整量

如表4所示。

4 多組試驗參數組合的均值調整表

（3）確定調整后質量損失最小的參數設計方案。計算表4中均值調整后各參數組合下輸出質量特性值均值的均值以及均值的方差。然后計算各參數組合下的信噪比。比較各參數組合下信噪比的大小，選取信噪比最大的參數組合，即為最優參數組合方案。

3 案 例

在電子產品的電路設計中，發現電子產品的輸出質量特性值與其元器件參數的水平之間存在著非線性關系。質量特性值高于或低于目標值時，產品散熱、零件承受能力等因素會引發電子元器件參數的非線性變化，使得參數偏離目標值的程度不同而帶來目標值兩側的質量損失不同，形成不對稱質量損失函數。現以電感電路的參數設計為案例來驗證本文研究的參數設計方法。

電感電路由電阻R、電感L和一個電源組成，電阻R受熱情況下電阻值會發生變化，導致電阻性能改變。當輸入交流電壓u和電源頻率f時，輸出電流強度

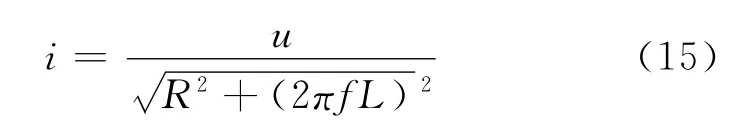
當電流強度圍繞目標值上下波動時，電流產熱會引發電感電路周邊的溫度發生變化，進而引發電阻R、晶體管等零件性能改變，使質量特性值在目標值兩側波動時產品的質量損失不對稱。

通過分析產品生產過程中的材料損耗以及返廠維修、產品報廢等數據，對產品的散熱情況進行統計，并確定由于散熱不及時導致返廠維修的費用，得出電流強度目標值兩側對應的質量損失函數為

在輸入電壓u=100±10 V 和頻率f=55±5 Hz的條件下，輸出電流強度目標值im=10 A，由電流可確定電壓u、電阻R、電感L和頻率f的因子水平表，如表5所示。

表5 因子水平表

將R和L的每個水平進行組合，而后進行重復試驗，并利用數據進行正交實驗，選取3水平正交表L9（34）進行試驗，而后計算各組合的均值μ、方差σ2、信噪比SN以及質量損失L。并計算目標值im左右兩側的均值和方差，并求其信噪比SN，如表6所示。

表6 目標值兩側均值、方差、信噪比及質量損失

比較各參數組合的信噪比可知，質量損失最小的參數組合與信噪比最大的參數組合相同，即為第G 組，所以，試驗選取第G 組參數組合為最優參數組合。下一步進行靈敏性設計：

在均值調整目標值μ*的確定中，由于r=k1/k2=3，查表2得λ*=0.436 326 6。

選取第G 組參數組合下質量特性值的方差σ2*=0.597 399 345，由μ*=m-σ*λ*得到均值調整目標值μ*=9.739 339。

在均值的波動分析中，將供電電壓u和供電頻率f作為噪聲因子，每組參數組合在不同的噪聲因子條件下進行重復實驗，得到各參數組合輸出質量特性的均值，并計算各組參數組合下均值的均值和均值的方差。

參數R、L因子及噪聲因子u、f的水平設置如表7所示。

表7 考慮噪聲因子的水平設置

可控因子（R，L）有9種組合，在每一種組合下，通過設計噪聲因子并進行重復試驗，此時，依然使用4因子3水平的正交表進行設計，即L9（34）。一次試驗結束后，會得到一個均值μ和方差σ2。然后模擬不同的外界環境，調整不同的噪聲因子并進行重復試驗，共進行18組，此時可得到每一種參數組合下的一組均值，對其進行均值的均值和均值的方差的計算，具體數據如表8～10所示。由表中數據，傳統的方法調整目標值后就完成了參數設計，得出的最優 參 數 組 合 為 第E 組（9.5，0.02），其 損 失L（x）=7.210 964 467。

而本文通過相關產品的電路等的設計，實現產品特性均值的移動，使均值的均值與目標調整值重合，其相應的移動量Δ=μ*-（m-σ*λ*），而后多次試驗，通過調整參數，使均值的波動減小，結合上文穩健性和靈敏性設計，產品的質量波動達到最小，使其損失降到最低，同時，由于分段計算質量損失，函數式能準確地度量在電阻R影響下每一段的損失值，比較損失值的大小，判斷損失最小的參數組合為第I組，即最優的參數組合為（10，0.025），質量損失L（x）=6.200 069 665。

表8 數據移動調整前的數據

表9 數據移動調整后的數據

表10 調整后數值的運算列表

4 結語

在實際生活中，大量產品設計過程中質量特性值偏離目標值時，產品造成的損失并不對稱，如果參數設計不合理，會給生產者以及社會帶來不必要的損失。例如，隨著智能手機的普及，其CPU 處理器在生產過程中就不得不考慮采用怎樣的電阻及晶體管材料才能避免因散熱原因導致的處理器性能下降和損失增加的問題。本文在非對稱質量損失情況下，利用分段函數度量波動帶來的質量損失，同時用正交試驗進行參數設計，討論了質量特性值對零件性能參數存在影響時，產品波動損失不對稱的情況。首先進行穩健性設計，在正交實驗設計中，通過信噪比確定穩健設計方案。并在穩健性設計的基礎上進行靈敏性設計，以質量損失最小為目標，確定最優均值點，調整均值到最優值，再進行質量損失的分段計算，確定總質量損失最小的參數設計方案。本文在非對稱質量損失函數情況下，利用分段函數度量質量損失的參數設計方案，還原了函數原有的形狀，最直接的質量損失計算，提高了質量損失度量的精確性，以此為目標進行的質量參數設計方案更符合實際。