一種基于模擬退火的參數自適應差分演化算法及其應用

李亞楠 ，郭海湘 ，黎金玲，劉曉

（中國地質大學1a.經濟管理學院；1b.數字化商務管理研究中心；1c.中國礦產資源戰略與政策研究中心，武漢 430074；2.武漢工程科技學院，武漢 430200）

差分演化算法[1]（Differential Evolution，DE）是Price等為求解切比學夫多項式問題于1995 年提出的一種演化算法，是基于群體的隨機搜索算法。算法最新穎的特點是它的變異操作，其操作是通過對當前個體加上2個隨機選定個體的帶權差來進行變異。因此，在算法迭代初期因種群個體差異較大，使得算法具有較強的全局搜索能力，但到了算法趨于收斂的迭代后期，種群個體差異較小，使得算法具有較強的局部搜索能力。這種新穎的變異操作也使得差分演化算法在求解優化問題上具有其他進化算法不可比擬的優點。主要總結為：收斂速度快、不易陷入局部最優及通用性強。而其包含的控制參數主要是種群大小、個體維度、變異因子以及交叉概率，待定參數較少。因其收斂速度快、不易陷入局部最優、通用性強、待定參數少等優點，差分演化算法被廣泛應用于全局優化、運籌管理和工程設計等領域[2-4]。

標準的差分演化算法在高維數、多峰值復雜函數的應用上容易出現“早熟”現象，即容易陷入局部最小；后期收斂速度較慢，表現不夠穩健；對控制參數設置及差分策略的選擇比較敏感，會影響差分演化算法的通用性。為此，許多學者對標準的差分演化算法進行了改進。Brest等[5]提出了一種改進的差分演化算法（jDE），算法對縮放因子和交叉概率進行了自適應的調整；Wang等[6]提出了一種策略和控制參數的混合式差分演化算法（CoDE），其中縮放因子和交叉概率選自已有研究中表現較好的值；Qin等[7]提出了一種自適應策略的差分演化算法（SaDE），使得算法能夠根據具體情況進行差分策略的選擇；Zhang等[8-9]提出了一種帶有存儲機制的自適應差分演化算法（JADE），在算法中給出了一種改進的DE/current-to-best/l差分策略；Mallipeddi等[10]提出了一種控制參數和差分策略整體自適應的差分演化算法（EPSDE），對控制參數和差分策略進行了匹配；Ghosh等[11]提出了一種基于適應度值的控制參數自適應方法的差分演化算法（FiADE），其中縮放因子和交叉概率根據目標的適應度值進行自適應調整；Pan等[12]提出了一種自適應的差分演化算法，其中每個個體對應一對單獨的縮放因子和交叉概率；Zou等[13]提出了一種改進的差分演化算法（MDE），其中交叉概率分別使用高斯分布和均勻分布生成，旨在提高種群多樣性；鄭建國等[14]提出了一種改進的差分演化算法，設計了一種新穎的DEB 準則[15]用于選擇操作。雖然在提高差分演化算法的搜索能力和收斂速度方面已經做了很多工作，但是自適應策略變得越來越復雜，而且已有研究文獻的仿真結果表明，差分演化算法的性能方面還有很大的改進空間。

本文提出了一種基于模擬退火的參數自適應差分演化算法（Enhanced Self-adaptive Differential Evolution，ESADE），在算法中先對種群進行初始化，生成2個相同的種群。同時，初始化一組控制參數，接著對這組控制參數進行簡單的差分計算，即對其進行差分演化算法中的變異操作，生成一組新的控制參數，這兩組控制參數分別和2個種群相對應。然后，2個種群在兩組不同的控制參數下進行變異、交叉操作，生成兩組試驗向量。在選擇操作中，通過對兩組試驗向量的比較后選出適應度表現最優的試驗向量作為下一代的目標向量。為了提高算法的全局搜索能力，本算法將模擬退火的思想應用在選擇操作上，并將表現較好的控制參數作為下一代初始化的控制參數。在這個進化過程中，每個目標向量對應的控制參數都能在學習前代優良經驗的基礎上逐步地進行自適應，解決了傳統差分演化算法對控制參數設置比較敏感這一問題。為了測試ESADE算法的性能，本文將ESADE 算法與jDE、JADE、SaDE、EPSDE及CoDE算法進行了比較，比較結果表明，ESADE算法的性能在整體上優于其他5 種算法。同時，為了測試ESADE 算法解決實際問題的能力，本文將ESADE 算法應用于TSP 問題，結果表明，ESADE算法能夠有效解決TSP問題。

1 傳統的差分演化算法及其變形

差分演化算法的主要思想是通過變異操作產生變異個體，然后進行交叉操作得到試驗個體。最后，通過選擇操作使得較好的個體進入下一代群體。由于差分演化算法涉及參數少，容錯性好，有全局優化的功能并且易于編碼實現，故此后被廣泛應用于各種科學領域。但差分演化算法也存在缺點，例如對控制參數設置及策略的選擇比較敏感，這些問題影響了差分演化算法的通用性，為了解決這些問題，很多改進的差分演化算法被提出。

1.1 傳統的差分演化算法

差分演化算法包括初始化種群、變異、交叉和選擇4個基本操作[16]，基本執行過程如圖1所示。

圖1 差分演化算法的基本流程

在圖1的基礎上，對差分演化算法的4個基本操作做進一步闡述。

（1）編碼。差分演化算法是一種基于種群的全局優化算法，種群中的個體均采用實數編碼。

（2）個體結構。用NP表示種群大小，種群中第i個個體在第G代記為

其中，D為個體所包含的維度。

（3）初始化種群。種群初始化采用公式

其中：xj，i，0為第G=0代，種群中第i個個體第j個維度的值；randi，j（0，1）∈[0，1]并且隨機生成；

為搜索空間第j個維度的下界；

為搜索空間第j個維度的上界；Xmin和Xmax分別為搜索空間的下界和上界的向量表達形式。

（4）變異。差分演化算法的差分就是體現在變異操作上，變異的一般過程為

式中：Xk，G為當前種群中待變異的第k個體；Xm，G、Xi，G、Xj，G為當前種群中隨機挑選的個體，并且k≠m≠i≠j；Vk，G為變異后的個體；F∈[0，1]為縮放因子。通常用DE/x/y/z表示不同的變異模式，DE表示差分演化算法；x為差分項前面的基礎項，通常有rand（基礎項是隨機從種群中選擇的個體）、best（基礎項是種群中最優個體）、rand-to-best和current-to-best等；y為差分項個數，通常取1或2。z為交叉模式，通常為指數模式和二項式模式。

（5）交叉。交叉概率Cr∈[0，1]。交叉有兩種形式：①指數模式為

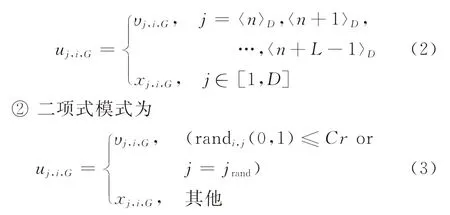
式中，jrand∈[1，2，…，D]為隨機選擇的值。

（6）選擇。交叉后得到的個體Ui，G和目標個體Xi，G分別代入目標函數進行比較，因為差分演化算法求的是目標函數極小，所以其選擇過程為

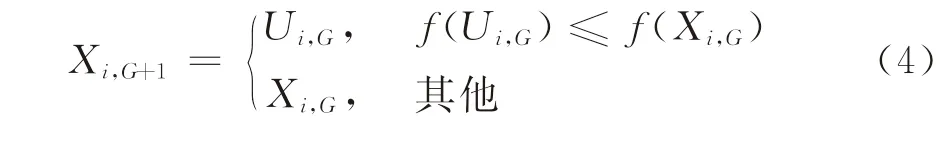
1.2 5種改進的差分演化算法

1.2.1 jDE算法 在jDE算法[5]中，控制參數F和Cr在進化過程中是自適應的，在編碼時，控制參數F和Cr被編碼在個體中，它們的調整是通過2個新的調整變量τ1和τ2。新一代的控 制參數Fi，G+1和Cri，G+1在變異操作之前就產生了，因此，jDE的這種自適應控制參數機制能夠影響到變異操作、交叉操作以及選擇操作生成的新個體向量。

1.2.2 JADE算法 在JADE 算法[8-9]中引入了一種新穎的變異策略（即DE/current-to-pbest 策略）和一個用于存檔次優解的存檔向量來引導算法進化的方向。這種DE/current-to-pbest 策略利用多個最佳解決方案既滿足了變異策略的貪婪性又保留了種群的多樣性，同樣地，這種存檔向量用來存儲除最優解外的較優解，能夠保留種群的多樣性。

1.2.3 SaDE算法 在SaDE算法[7]中，每一代的差分策略是從策略侯選池（DE/rand/1，DE/rand/2，DE/rand-to-best/2，DE/current-to-rand/1）中，根據每個差分策略概率的大小進行選擇，這個概率是通過對每個差分策略在一定數量的代數上的表現進行計算的，其中這個一定數量的進化代數稱為學習期（Learning Period，LP）。

1.2.4 EPSDE算法 在EPSDE 算法[10]中引入了差分策略池和控制參數池，其中控制參數池包括縮放因子值池和交叉概率值池。

在EPSDE算法中，初始化種群中每個個體隨機地從差分策略池中選擇一種差分策略，并相應地從縮放因子值池和交叉概率值池中分別隨機選取一個值作為其縮放因子和交叉概率。在選擇操作中，當試驗向量的適應度值比目標向量的適應度值好時，生成試驗向量對應的差分策略、縮放因子和交叉概率的組合將被保存在一個成功組合池里，并進入下一代的進化；當試驗向量的適應度值比目標向量的適應度值差時，目標向量對應的差分策略、縮放因子和交叉概率將被隨機重新初始化，該初始化過程是以相同的概率直接從成功組合池中隨機選擇，或從差分策略、縮放因子和交叉概率各自對應的池中隨機選擇。

1.2.5 CoDE 算法 類似地，Wang等[6]提出了一種結合不同差分策略的系統框架，稱為復合式差分演化算法（Composite DE，CoDE）。其中差分策略和控制參數是通過研究后選取表現較好的策略和參數值。

在CoDE算法中，對應3種差分策略，每個目標向量進行差分演化計算后生成3個試驗向量。將3個試驗向量中適應度值表現最好的一個與目標向量的適應度值進行比較，如果其適應度值表現比目標向量的適應度值好，則該試驗向量將進入下一代進化。

2 基于模擬退火的參數自適應差分演化算法

針對傳統差分演化算法對控制參數設置和差分策略選擇比較敏感，以及局部搜索能力較差導致的演化后期收斂速度變慢等問題，已經有很多學者對傳統差分演化算法提出了改進策略，雖然在提高差分演化算法的搜索能力和收斂速度方面已經做了很多工作，但是自適應策略變得越來越復雜，而且已有研究文獻的仿真結果表明，差分演化算法的性能方面還有很大的改進空間。基于這種情況，本文提出了一種基于模擬退火的參數自適應差分演化算法（ESADE），其步驟如下：

（1）個體編碼。編碼個體包括三部分：候選解向量、控制參數和適應度值。編碼個體結構如圖2所示。

圖2 個體的編碼

（2）初始化。初始化包括控制參數初始化和種群初始化兩部分。其中，控制參數初始化包括種群大小NP，模擬退火中初始溫度參數t0，每個個體對應的縮放因子oFi，G和每個個體對應的交叉概率oCri，G。其中，oFi，G和oCri，G的動態更新如下：

式中，oFi，G、oCri，G分別是以μF和μCr為均值通過柯西和正態分布生成的。μF、μCr初始值設置為0.5，每一代的更新過程分別為：

式中：SF是用來存儲成功進化縮放因子的數組，即用來存儲能夠進入下一代的試驗向量對應的縮放因子值的數組；SCr是用來存放成功進化交叉因子的數組，即用來存儲能夠進入下一代的試驗向量對應的交叉因子值的數組。

種群初始化是在相應范圍內均勻分布，

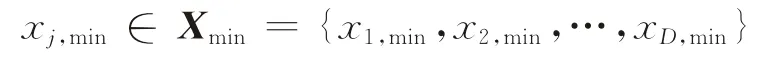
并且

則在G=0代時，第i個個體第j個屬性的初始化為

（3）參數變異。通過對控制參數oF和oCr進行變異操作，得到一組新的控制參數mF和mCr，其變異過程為：

式中，r1、r2的取值是在1，2，…，NP中隨機抽取不同的整數。

生成2個相同的種群：①標記為populationo，與控制參數oFi，G、oCri，G對應進行差分演化計算；②標記為populationm，與控制參數mFi，G、mCri，G對應進行差分演化計算。

（4）種群變異操作。種群populationo的差分策略是DE/current-to-pbest/1，其變異操作過程為

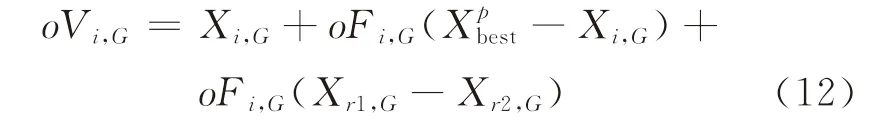
種群populationm的差分策略是DE/current-topbest/1，其變異操作過程為

（5）種群交叉操作。種群populationo的交叉操作是二項交叉，其操作過程為

種群populationm的交叉操作是二項交叉，其操

作過程為

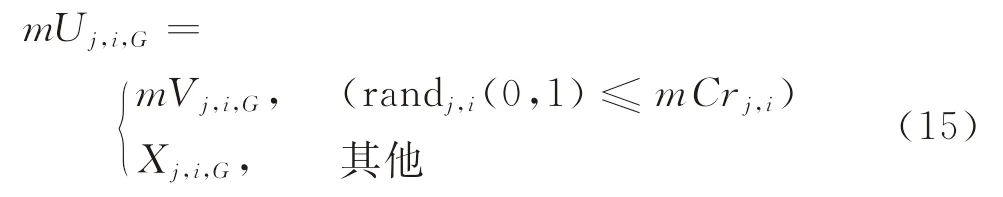
（5）種群選擇操作。種群選擇操作的過程是通過比較目標向量Xi，G、種群poplutiono生成的試驗向量oUi，G以及種群poplutionm生成的試驗向量mUi，G選擇出適應度值最優的進化到下一代。在該過程中，模擬退火的思想被加入到選擇操作中用來增強算法的全局搜索能力，t0為模擬退火中的初始化溫度參數，tG為第G代溫度參數，其中，tG更新與選擇操作過程為：

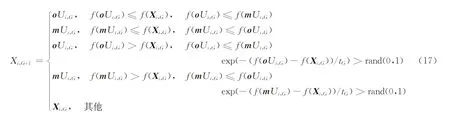
式中：G為進化的第G代；f（oUi，G）為oUi，G的適應度值；f（mUi，G）為mUi，G的適應度值；f（Xi，G）為Xi，G的適應度值。

（7）記錄優良的控制參數。當試驗向量能夠成功進化到下一代時，說明其對應的控制參數表現較好，這些表現較優良的控制參數將分別被存入成功進化縮放因子數組SF和成功進化交叉因子數組SCr中。其過程為：

若Xi，G+1=oUi，G，則oFi，G→SF，oCri，G→SCr；若Xi，G+1=mUi，G，則mFi，G→SF，mCri，G→SCr。

當數組SF、SCr內存儲的控制參數數量超過一個上限值時，數組SF、SCr將被清空。

（8）更新控制參數。如果SF不是空集，則根據（7）、（5）對控制參數oF進行更新，更新過程：

如果SCr不是空集，則根據（8）、（6）對控制參數oCr進行更新，更新過程：

3 ESADE 算法與差分演化算法的其他變形的比較

3.1 實驗設置

3.1.1 基準函數 影響差分演化算法計算效果的因素主要包含實驗環境、測試函數和控制參數的設置以及差分策略的選擇。為了測試ESADE 算法的性能，本文將ESADE算法與其他改進差分演化算法在相同條件下進行測試。因為改進的差分演化算法大多是針對變異因子、交叉概率以及差分策略進行的改進，因此，本文設置的相同條件主要包括相同的實驗環境（電腦型號Dell-XPS8500和軟件型號Matlab-R2010a）、相同的測試函數以及相同的基本參數（種群大小、個體維度、算法進化的代數以及獨立運行次數）。本文使用17（f1～f17）個全局最小值的基準函數作為測試函數，這些函數都是從參考文獻[15]中選擇的國際通用的測試函數，其維度均可以自由變化。其中，f1～f5是單峰函數，f6～f9是基本多峰函數，f10是擴展多峰函數，f11～f17是混合組成函數。這些函數的最優值f（x*）、最優取值時x*的取值和x的初始范圍如表1所示，函數的詳細表達形式見附錄A。

表1 基準函數的基本介紹

3.1.2 參數設置 為了比較ESADE 算法和其他改進差分演化算法的性能，本文設置統一參數：進行基準函數測試的維度大小D=30；種群大小NP=50；每個函數的最大進化代數為10 000；每個函數獨立運行次數為25。另外，本文提出的算法所涉及模擬退火中的初始化溫度參數t0=1 000。

3.2 ESADE算法和其他改進差分演化算法性能的比較

ESADE算法性能的評估是通過和其他改進差分演化算法的性能進行比較而得出的，這些改進差分演化算法是上文所介紹的jDE、JADE、SaDE、EPSDE和CoDE等5種算法。

為了避免一次運算導致的結果偏差較大這一現象，本文設置的獨立運行次數為25，即每個函數進行25次獨立進化，對進化的最優值求平均作為算法求得的平均最優值。表2給出了17個基準函數在維度取值為30、獨立運行次數為25 時的平均值。為了進一步分析算法的性能，本文采用威爾科克森秩和檢驗分別對ESADE算法和jDE、JADE、SaDE、EPSDE及CoDE算法進行了比較，其中威爾科克森秩和檢驗的置信區間為0.05，其比較結果如表3所示。

表2 ESADE算法和jDE、JADE、SaDE、EPSDE及CoDE算法在17個測試函數上進行25次進化的測試結果

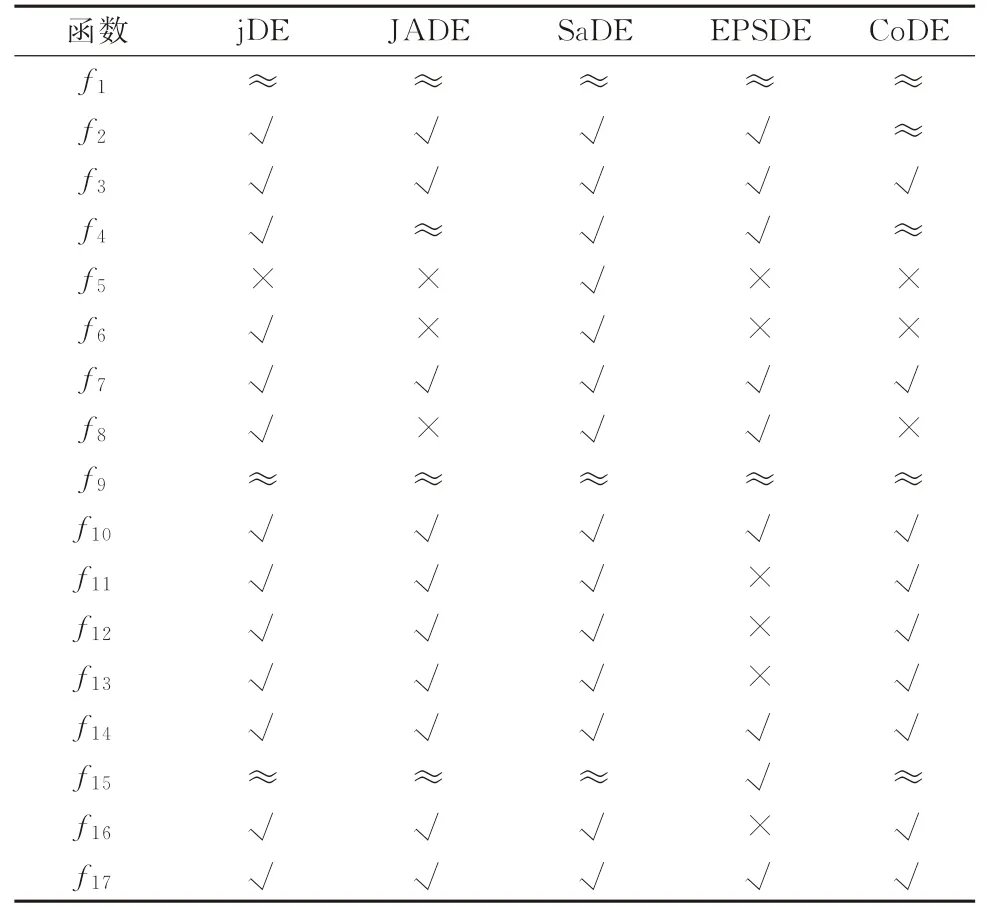
表3 威爾科克森秩和檢驗的比較結果

表4給出了ESADE 算法和其他改進差分演化算法之間的比較結果。表4清楚地表明，本文提出的ESADE算法整體上比其他5種算法的性能都要好。如ESADE 算法在13 個測試函數上性能比jDE算法好，在3個測試函數上性能和jDE相似；在10個測試函數上性能比JADE 算法好，在4個測試函數上性能和JADE相似；在14個測試函數上性能比SaDE算法好，在3 個測試函數上性能和SaDE相似；在9個測試函數上性能比EPSDE 算法好，在2個測試函數上性能和EPSDE相似；在9個測試函數上性能比CoDE 算法好，在5個測試函數上性能和CoDE相似。

表4 ESADE算法和CoDE、JADE、j DE、EPSDE算法及SaDE在威爾科克森秩和檢驗下的比較結果

為了進一步闡明ESADE 算法和其他改進差分演化算法性能之間的關系，本文在圖3中給出6個測試函數在幾種不同算法上的進化收斂圖。由圖3可見，ESADE算法的整體收斂速度比其他5 種算法都要快，而且沒有出現陷入局部最優的情況。圖3中所選取的6個測試函數都是有代表性的函數。從ESADE 算法和其他改進差分演化算法的比較表明，ESADE算法的性能在整體上優于其他5 種算法，與其他5種算法相比，ESADE 算法的優勢很明顯。這是因為本文提出的ESADE 算法能夠自適應地調整控制參數以便滿足不同問題需求，而且在選擇操作中加入了模擬退火的思想，能夠提高全局搜索能力。

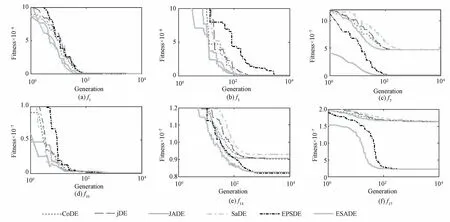
圖3 ESADE、jDE、JADE、SaDE、EPSDE和CoDE算法在6個函數上的進化收斂圖

3.3 模擬退火中初始溫度參數對ESADE 算法性能的影響

模擬退火中初始溫度參數的設置可能會影響ESADE算法的性能，為了使ESADE算法的性能達到最優，本文對模擬退火中初始溫度參數t0的取值進行了測試。在t0=10，100，1 000，10 000時，分別測試了ESADE算法的結果并給出了ESADE 算法在6個函數上的收斂圖，如圖4所示。圖中表明，當t0=10 000 時，ESADE 的性能較差；但是當t0=10，100，1 000時，并無明顯區別。為了進一步說明t0取值對ESADE 算法性能的影響，本文使用威爾科克森秩和檢驗分別對取不同t0值的ESADE算法和jDE、JADE、SaDE、EPSDE 及CoDE 算法進行了比較，其中威爾科克森秩和檢驗的置信區間為0.05，其比較結果如表5 所示。表中說明，當t0=1 000時，ESADE算法的性能最好。故將初始溫度參數設置為t0=1 000。

表5 t0取不同值時，ESADE 算法和CoDE、JADE、jDE、EPSDE 及SaDE算法的比較結果

圖4 t0取不同值時，ESADE算法在6個函數上的收斂圖

3.4 ESADE算法在解決TSP問題上的應用

為了測試ESADE算法在解決現實問題上的性能，本文將ESADE 算法用于解決TSP 問題，并將結果與CoDE、JADE、jDE、EPSDE 及SaDE 算法進行比較。

3.4.1 TSP問題描述 TSP（Traveling Saleman Problem）即旅行商問題，簡稱為TSP 問題，是最基本的路線問題，該問題是在尋求單一旅行者由起點出發，通過所有給定的需求點之后，最后再回到原點的最小路徑成本[16]。在算法中，通過目標函數來評價新解的優劣，從而保證產生新解的質量，有利于算法的快速收斂。本文使用的目標向量為

式中：n為城市個數；dij為城市i、j之間的距離；xij為決策變量，其表達式為

3.4.2 實驗設置 所有算法的最大進化代數統一設置為10 000，種群大小為100，獨立運行次數為25次，城市個數分別為10和14（城市的具體坐標見附錄B）。

3.4.3 實驗結果與分析 表6給出了當ESADE、CoDE、JADE、jDE、EPSDE 及SaDE 算法用于TSP問題的結果以及時間消耗。結果表明，當城市個數為10 和14 時，ESADE 算 法 能 夠 得 到 與jDE、JADE、SADE 及CoDE 算法相同的平均值和中值，并且這一均值是目前已有研究中的最小值；同時，因為ESADE 算法中采取的雙種群策略以及加入模擬退火機制的選擇策略，相對于jDE 和JADE 算法，ESADE時間耗費會翻倍，但比SaDE、EPSDE 和CoDE 算法的時間耗費，ESADE 算法更高效。表7給出了在0.05置信區間內，本文采用威爾科克森秩和檢驗分別對ESADE 算法和jDE、JADE、SaDE、EPSDE及CoDE算法應用于TSP問題上的結果進行了比較，比較結果表明，ESADE算法在TSP問題上的表現優于EPSDE 算法，類似于jDE、JADE、SADE及CoDE算法。以上結果表明，ESADE算法能夠有效解決TSP問題。

表6 ESADE、CoDE、JADE、jDE、EPSDE及SaDE算法應用于TSP問題的結果

表7 ESADE算法和CoDE、JADE、j DE、EPSDE及SaDE算法在TSP問題上的比較結果

4 結語

差分演化算法作為一種高效的優化算法，被廣泛應用于科學與工程領域。在差分演化算法中，進化策略和控制參數會對算法的性能有重要影響。但是因為不同問題甚至是相同問題的不同進化階段需要的最優設置都是不同的，使得選擇合適的進化策略和相關參數成為一個較困難的問題。為了解決該問題，本文提出了一種ESADE算法。ESADE算法生成一組控制參數oF和oCr，再通過對這組控制參數進行變異操作生成一組新的控制參數mF和mCr，然后根據這兩組控制參數分別對2個相同的種群進行變異和交叉操作，生成兩組試驗向量，最后進行選擇操作。為了增強算法的全局搜索能力，ESADE算法中的選擇操作加入了模擬退火的思想。為了對ESADE 算法的性能進行測試，本文從CEC2005中選擇了17個函數作為測試函數，并將ESADE算法的測試結果與其他改進差分演化算法的測試結果進行了比較。比較結果顯示，ESADE算法有很強的全局搜索能力，并且性能在整體上優于其他算法。同時，本文還測試了模擬退火中初始溫度參數對ESADE 算法性能的影響，結果表明，當初始溫度參數為1 000時，ESADE算法的性能較好。最后，將ESADE算法應用于TSP問題，結果表明，ESADE 算法能夠取得與jDE、JADE、SADE及CoDE算法相同的最小值，并且這一最小值是目前已知最小值，這說明，ESADE算法能夠有效解決TSP問題。

本研究未來的工作主要集中于兩點：①將小生境算法的思想加入到變異操作中，改變個體的選擇方式，使得個體的選取更加具有代表性；② 將ESADE算法應用于解決更多的實際問題，例如，將ESADE算法用于解決多目標優化問題；將ESADE算法用于解決油層識別問題，包括特征選擇和規則提取等。

附錄A

基準函數的詳細表達形式。

f1：Shifted sphere function，其公式為，z=x-o，其中，-100≤x（i）≤100，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。

f2：Shifted schwefel's problem 1.2，其公式為，z=x-o，其中，-100≤x（i）≤100，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。

f3：Shifted rotated high conditioned elliptic function，其公式為，z=（x-o）M，其中，-100≤x（i）≤100，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0，M為正交變換矩陣。

f4：Shifted schwefel's problem 1.2 with noise in fitness，其公式為

其中，-100≤x（i）≤100，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。

f5：Schwefel's problem 2.6 with global optimum on bounds，其公式為，其中，-100≤x（i）≤100，A為D×D的矩陣，aij是取值范圍在[-500，500]的隨機整數，det（A）≠0，Ai是矩陣A的第i行，Bi=Ai˙o，o是D×1的向量，oi是取值范圍在[-100，100]的隨機整數，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。

f6：Shifted rosenbrock's function，其公式為

其中，-100≤x（i）≤100，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。

f7：Shifted rotated griewank's function without bounds，其公式為

其中，0≤x（i）≤600，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0，M為正交變換矩陣。

f8：Shifted rotated ackley's function with global optimum on bounds，其公式為

其中，-32≤x（i）≤32，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0，M為正交變換矩陣。

f9：Shifted rastrigin's function，其公式為，z=x-o，其中，-5 ≤x（i）≤5，o=（o（1），o（2），…，o（n））為轉移全局最優取值，即全局最優值在x*=o時取得，全局最優值f（x*）=0。f10：Shifted expanded griewank's plus rosenbrock's function，其公式為

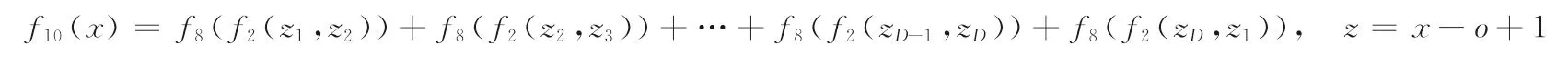
其中，-3 ≤x（i）≤1，o=（o（1），o（2），…，o（n））為轉移全局最優取 值，即全局最優值在x*=o時取 得，全 局最優值f（x*）=0。

f11～f17：函數f11～f17分別由10個基本函數組合而成，詳細描述請參考文獻[15]。

附錄B

城市坐標

表1 10點TSP問題

表2 14點TSP問題