無應力狀態法在拱肋線形調整中的應用

王胡鵬

（中鐵大橋科學研究院有限公司，湖北武漢 430034）

無應力狀態法在拱肋線形調整中的應用

王胡鵬

（中鐵大橋科學研究院有限公司，湖北武漢 430034）

以某采用纜索吊機斜拉扣掛法施工的大跨度鋼管混凝土拱橋為背景，探討了無應力狀態法在該類橋梁拱肋吊裝線形調整中的應用。通過推導扣索無應力長度變化量與索力變化量之間的關系，避免了傳統調索方法受調索次序影響的缺點，并在該橋實踐中進行了應用。結果表明，該方法用于拱肋線形調整可以滿足工程要求。本文提到的線形調整方法可供同類橋梁的施工控制參考。

無應力狀態法無應力長度鋼管混凝土拱施工控制

引言

纜索吊裝斜拉扣掛法是大跨度拱橋拱肋施工的一種主要方式[v]。該方法通過纜索吊裝系統將各個拱肋節段吊運到位，與已經施工好的拱肋節段對接，并通過千斤頂扣掛系統將其固定，直至合龍。該方法具有張拉能力大、索力調整方便、控制精度高和錨固可靠等優點。在實際施工中，由于誤差累積、索塔偏位、臨時荷載等影響，拱肋實際線形將偏離理論控制值。為了保證拱肋成拱后的內力與線形滿足設計要求，需要對拱肋線形進行監控[vi][vii]。當發現拱肋線形出現較大偏差時，可以通過張拉扣索進行調整，類似于斜拉橋中的“調索”。傳統的調索計算方法以索力作為控制量，每根索之間相互影響，某一根索力調整時，必將影響其他扣索。而無應力狀態法是指在一定的結構體系和作用體系下，通過精確控制結構構件的初始幾何尺寸與形態（結構內力狀態的控制為輔）來達到對橋梁結構最終成橋幾何形態和內力狀態控制的一種控制方法[viii][ix]。該方法以扣索的無應力長度作為控制量，直接得到扣索張拉前后索力增量與無應力長度變化量之間的關系，施工操作的自由度更大：通過計算扣索的無應力長度差，以錨頭拔出量（或放回量）調整拉索時，不受調索次序影響，精度更容易保證[x]。

工程背景

某橋主橋橋型為(60+180+60)m的飛雁式鋼管混凝土提籃式系桿拱橋，主橋長300m。主拱和邊拱拱軸線均采用懸鏈線，主拱計算跨徑180m，面內矢高45m，矢跨比為1/4，拱軸系數m=1.5，主拱拱頂間距為20.1m。邊拱計算跨徑120m，面內矢高16.021m，矢跨比為1/7.49，拱軸系數m=1.5。

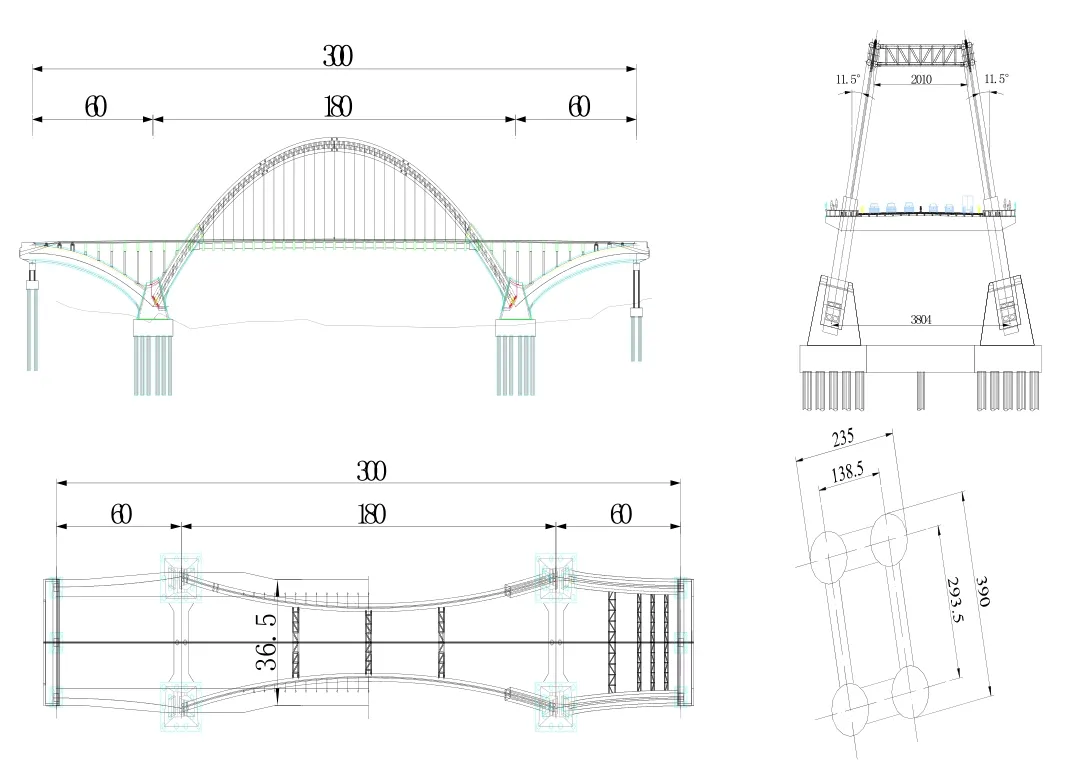
圖1 橋型布置圖

該橋主拱肋分節段在工廠預制而成，現場采用纜索吊機斜拉扣掛法施工。主拱肋節段劃分如圖2所示，沿主跨中心兩側對稱分為S1～S5（西岸）及S1’～S5’（東岸）共10個節段，中部設置合龍段。東、西兩岸各布置5對扣索，1#～5#扣索均采用鋼絞線，彈性模量均為195000MPa，有效斷面積分別為560、840、840、1120和1400mm2。

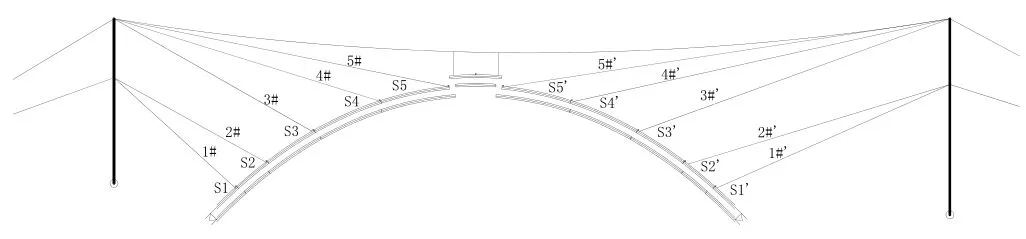
圖2 主拱肋節段劃分圖

該橋在主拱肋合龍前，西岸扣塔發生了較大的偏位，且在S5節段端部有一100kN的臨時荷載，因施工條件限制，需要在主拱肋合龍后才能拆除。如圖3所示，當前狀態下西岸半拱肋各扣點處標高偏差最大達到了-0.111m，如果不對拱肋線形進行調整，合龍段將無法以無應力長度安裝就位，主拱肋成拱后內力與線形也無法滿足理論要求。

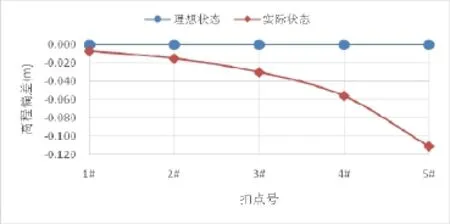
圖3 拱肋實際狀態高程偏差

扣索無應力長度變化量與索力增量關系推導

如圖4所示，設定扣索張拉前后兩個結構狀態，其中結構狀態1：扣索有應力長度為L1，無應力長度為L10，扣索斷面積為A，扣索的彈性模量為E，索力為F1，環境溫度為T1；通過給扣索施加張拉力，達到結構狀態2：即扣索有應力長度變為L2，無應力長度為L20，索力為F2，并假定扣索張拉到位時環境溫度為T2。

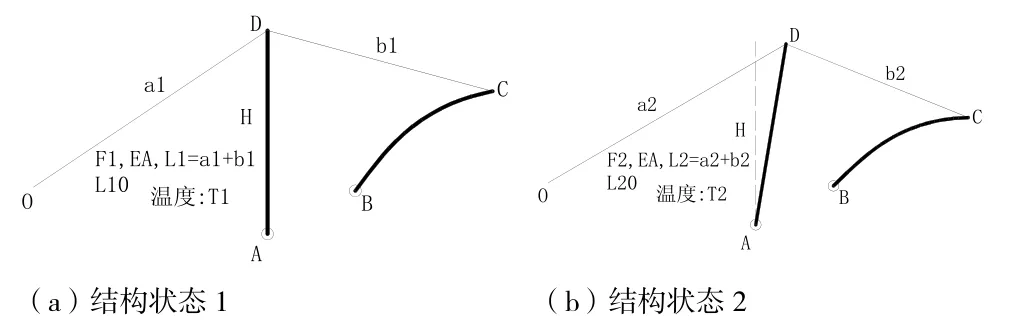
圖4 兩種結構狀態

根據以上描述，易得到如下關系式：

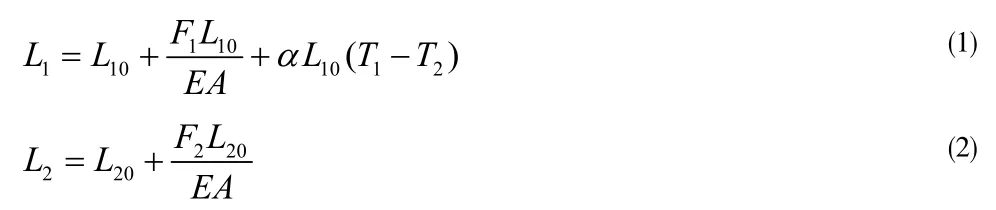
式(2)-式(1)，并整理可得：

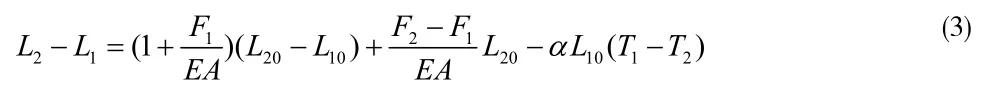
假設單位力引起的扣索有應力長度變化量為ε，即：

聯立式(3)、式(4)：

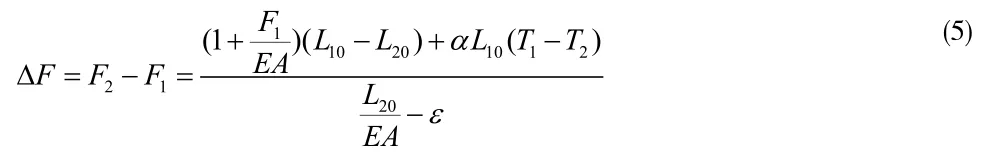
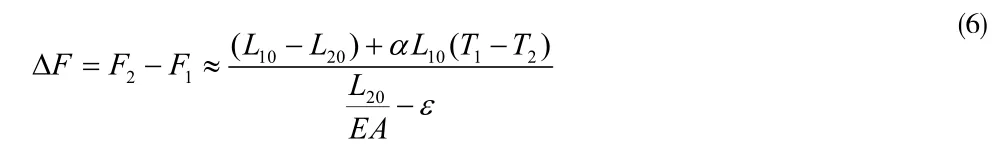
式(6)中，ε代表索兩端結構的剛度。可以看出，兩個結構狀態之間的索力增量ΔF只與其無應力長度L10、L20及兩個狀態的溫度T1、T2有關。因此，以無應力長度作為控制量，避免了傳統方法進行索力調整時受調索次序影響的缺點。

無應力狀態法進行拱肋線形調整

上一節推導了扣索無應力長度改變量與索力增量之間的關系。本節利用推導結果，利用midas Civil分別建立該橋理想狀態與實際狀態的計算模型，計算兩個狀態的扣索信息（包括：扣索錨點坐標、扣點坐標、無應力長度及當前階段的索力等）。

計算模型如圖5所示，兩個狀態扣索錨點坐標及索力信息分別如表1～表2所示。

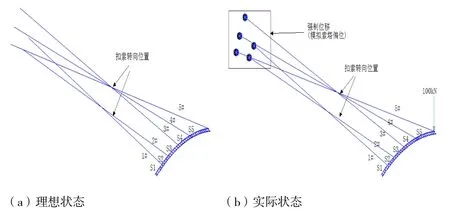
圖5 主拱肋大懸臂階段計算模型

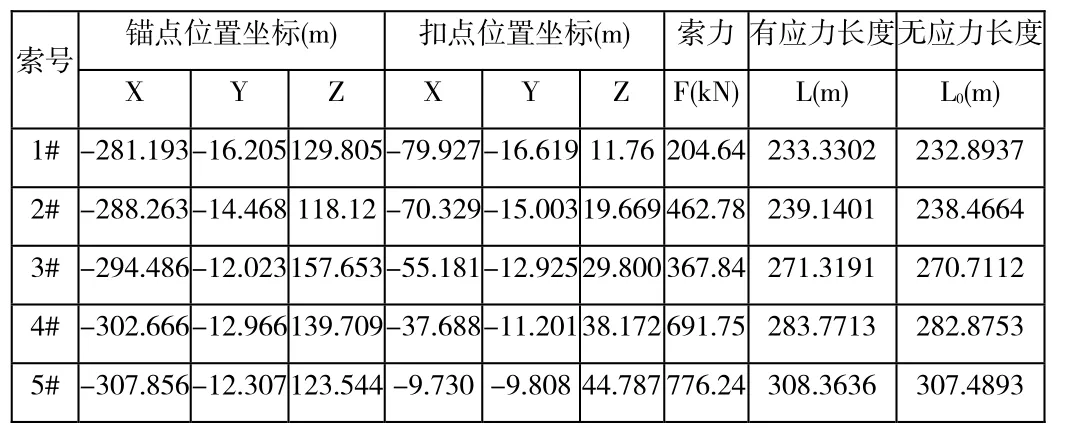
表1 理想狀態扣索信息表

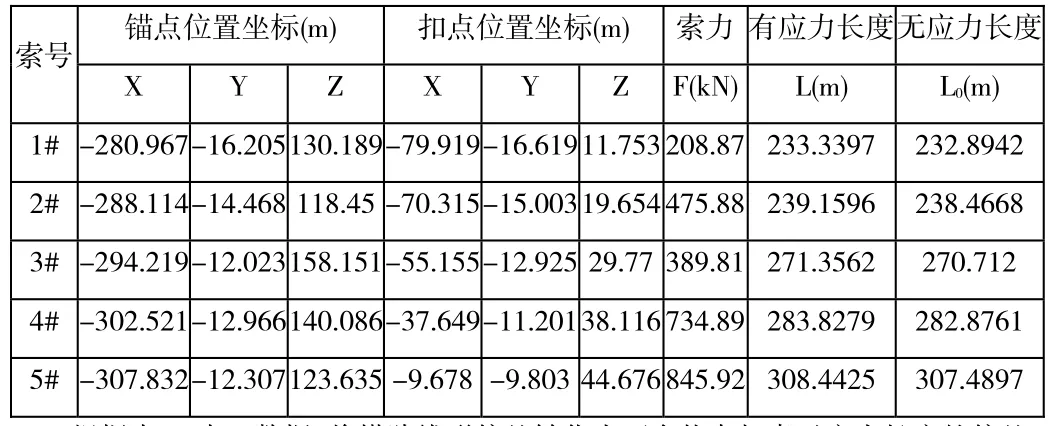
表2 實際狀態扣索信息表

根據表1、表2數據，將拱肋線形偏差轉化為兩個狀態扣索無應力長度的偏差，利用前述推導公式，容易計算出各扣索需要施加的調整力，如表3所示：

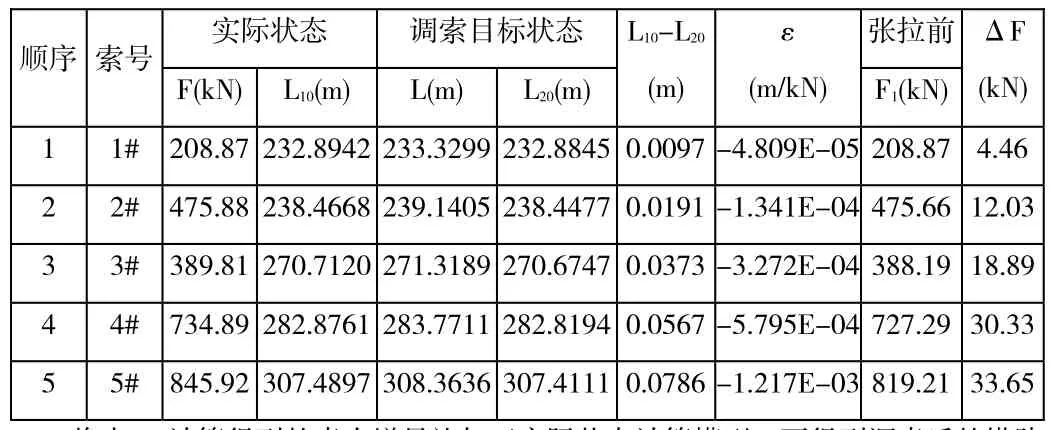
表3 拱肋線形調整索力增量計算表

將表3計算得到的索力增量施加于實際狀態計算模型，可得到調索后的拱肋線形。如圖6所示：通過張拉扣索進行線形調整后，各扣點高程偏差明顯減小。對線形進行調整后，主拱肋各控制點高程偏差值最大為-0.018m，小于L/3000=0.060m，滿足控制要求。

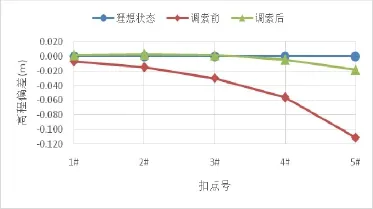
圖6 線形調整后各扣點高程偏差

結語

從以上分析結果可以看出，無應力狀態法通過扣索的無應力長度作為控制量，避免了傳統調索計算中受調索次序影響的缺點。同時，通過將拱肋線形偏差轉化為扣索無應力長度差的方式，確定出拱肋線形調整所需要的扣索張拉力。結果表明，該方法可以滿足工程要求，可供同類橋梁施工控制參考。

[1]陳寶春. 鋼管混凝土拱橋[M]. 第二版. 北京：人民交通出版社，2007

[2]向中富. 橋梁施工控制技術[M]. 北京：人民交通出版社，2001

[3]徐君蘭. 大跨度橋梁施工控制[M]. 北京：人民交通出版社，2000

[4]秦順全. 橋梁施工控制——無應力狀態法理論與實踐[M]. 北京：人民交通出版社，2007.2

[5]李喬等著. 大跨度斜拉橋施工全過程幾何控制概論與應用[M]. 成都：西南交通大學出版社，2009.4

[6]秦順全. 分階段施工橋梁的無應力狀態控制法[J]. 橋梁建設，2008（1）

TU714

B

1007-6344（2016）02-0236-02

王胡鵬（1988.03---），男，漢族，山西長治人，碩士研究生，中鐵大橋科學研究院有限公司，主要研究方向：大跨度橋梁施工控制及健康監測。