基于蒙特卡羅模擬的船體型線穩健優化設計

蔣國偉，馮佰威,2，常海超,2

(1.武漢理工大學 交通學院，湖北 武漢 430063；2.高性能船舶技術教育部重點實驗室，湖北 武漢 430063)

?

基于蒙特卡羅模擬的船體型線穩健優化設計

蔣國偉1，馮佰威1,2，常海超1,2

(1.武漢理工大學 交通學院，湖北 武漢 430063；2.高性能船舶技術教育部重點實驗室，湖北 武漢 430063)

傳統的船型優化僅考慮了確定性因素的影響，忽視了設計和使用中不確定性因素的存在，常導致船型方案不可行或航行性能較差。為了考慮不確定因素對船舶阻力性能的影響，在船型優化中引入穩健優化設計理論。首先，闡述了穩健優化設計的基本原理，在此基礎上，以KCS船型為例，考慮了航速不確定性的影響，建立了穩健優化數學模型。其次，基于Isight平臺完成了KCS船體型線穩健優化設計。試驗結果表明：船體型線穩健優化設計可有效地減小船型方案失效的可能性，更符合工程實際。

船型優化；隨機不確定性；穩健優化；興波阻力

0　引言

船體型線優化是一種有效的船舶節能技術，而優化模型的建立則是船型優化的關鍵。目前，大多數船體型線優化模型是建立在確定性優化理論基礎之上，在優化過程中，將設計變量作為確定性的量。而實際上，在船舶設計過程中，存在很多不確定性變量，例如由于生產精度導致船體參數達不到或者超過設計值；航行時會受到風、浪、流等因素的影響導致船舶的實際航速在設計航速附近波動等，這些不確定因素可能導致最優方案失效或者船舶性能達不到預定的設計目標。

目前，在船舶優化設計中考慮不確定因素的研究成果相對較少。江蘇科技大學邵偉等[1]利用最小波動法對某4萬t散貨船的中橫剖面結構進行了穩健優化設計。李冬琴等[2]在船舶設計優化中，考慮設計變量中航速和吃水的隨機不確定性及計算參數垂線間長和總長的隨機不確定性，以一艘平臺輔助船為研究對象，構建了不確定性優化數學模型，實現了船舶多學科穩健優化設計。Diez M等[3]提出了一種考慮環境變量不確定性的散貨船概念設計穩健優化方法，同時將期望值和方差作為優化目標，約束條件以最壞情況考慮，以單位運輸成本的期望值和方差最小為目標對散貨船進行了優化。

本文以某3 600 TEU集裝箱船KCS為研究對象，考慮船舶在實際航行過程中航速不確定性的影響，通過降低船舶興波阻力對航速的敏感度，使得優化后的方案不僅阻力有所下降，而且在設計航速附近阻力波動較小。

1　基于蒙特卡羅模擬法的穩健優化設計

基于蒙特卡羅模擬法的穩健優化設計方法是從統計學的角度出發，用概率模型來分析不確定因素對產品性能的影響，再依據概率分析方法來控制不確定性因素對產品性能的影響，獲得滿足產品性能、可靠性等各方面要求的設計方法[4]。在穩健優化設計中，通過改進設計變量的均值μ和均方差σ，能有效地降低產品性能對不確定因素的敏感度，提高產品的可靠度。

確定性優化解和不確定性優化解示意圖如圖1所示。從圖1中可以看出，如果不考慮變量x的波動，以確定性優化的收斂標準判斷，1點處目標函數最小，則1點為最優方案。如果考慮變量x在±Δx范圍內波動時，目標函數f(x)在該點的變化量Δf1超出了約束界限，有可能導致設計方案失效。在2點處由于變量x的波動引起的目標響應的變化值Δf2雖然沒有超出約束界限，但目標響應的波動依然較大，特別在2點左側目標值會隨著x的減小快速增大，該方案穩健性較差。3點處，在±Δx范圍內，目標函數的變化值Δf3有了明顯減小，穩健性有了提高，但目標響應的平均值變大了。可以看到，在3點右邊可能存在目標響應波動更低的區域，但其響應的均值有可能超出了理想值。因此，在穩健優化過程中，要合理的權衡目標響應的均值和降低響應的波動這2個指標[5]。

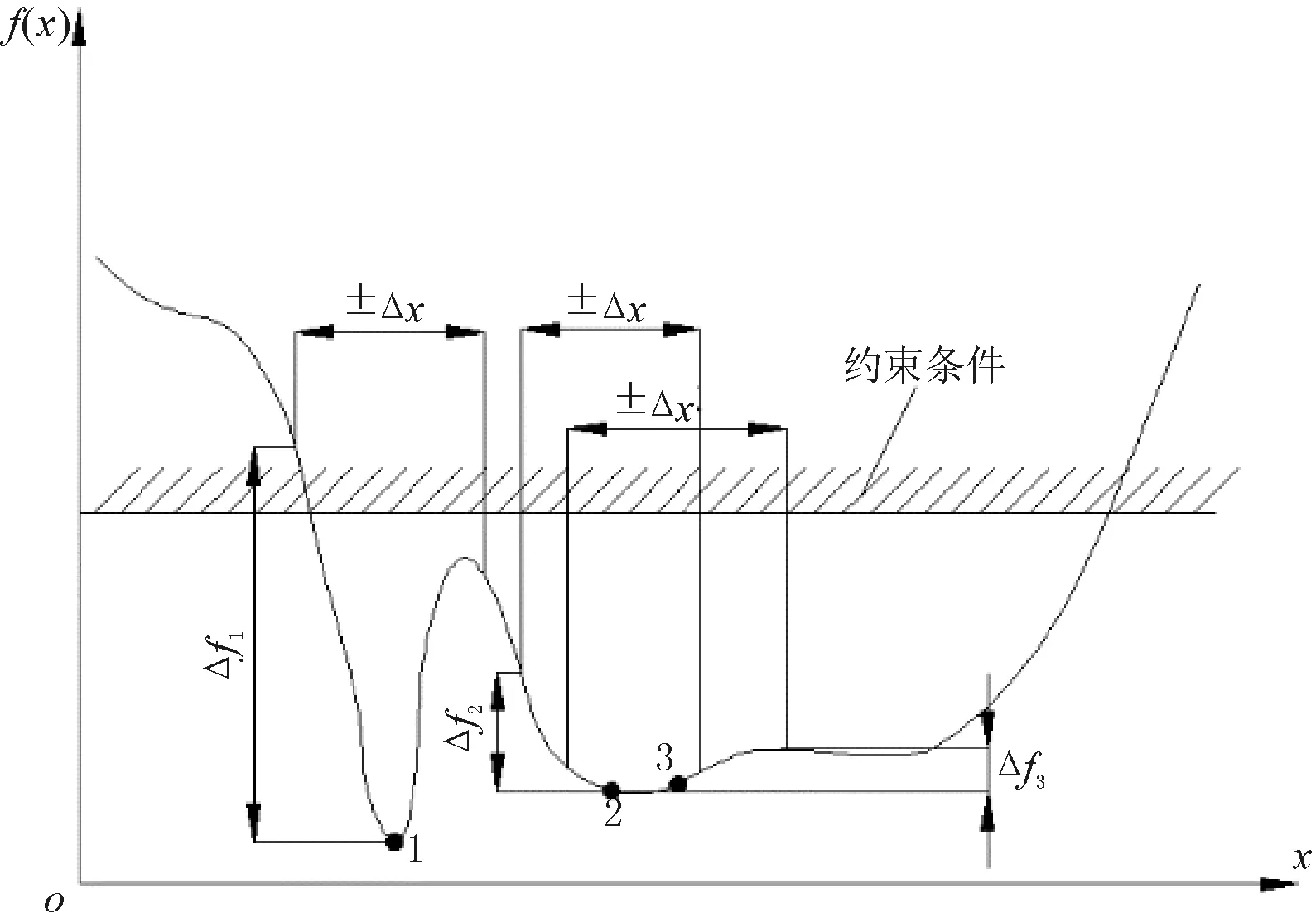
1.目標最小值　2.可靠最優值　3.穩健最優值

典型的穩健性優化公式為：

minF(μ，σ)

s.t.Gj(μ，σ)≤0xL+Δx≤x≤xU-Δx

(1)

式中：x為設計變量；Gj為約束函數；j為約束函數的數量；XL為設計變量的下限；xU為設計變量的上限。

目標函數F可以進一步分解為2個部分，即“最小化性能波動”和“達到平均性能目標”，故穩健性設計目標公式為：

(2)

式中：n為目標響應的數量；i為目標響應Y的分量下標；μY為目標響應Y的均值；σY為目標響應Y的均方差；W1和W2分別為目標響應Y的均值μY和均方差σY的權重系數；S1和S2分別為Y的均值μY和均方差σY的歸一化系數；Mi為期望達到的平均性能目標值[6]。

從式(2)中可以看到，均值和均方差的求解是穩健優化設計的核心。目前，蒙特卡羅模擬方法、矩陣法和解析法是應用較為廣泛的求解方法[7]，其中，蒙特卡羅模擬方法在概率特性評估方面被認為是最準確的方法，因此，本文采用該方法求解目標響應的均值和均方差。蒙特卡羅模擬技術(Monte Carlo Simulation，MCS)是利用抽樣理論代替求解物理或者數學問題的一種方法[8]。MCS方法的原理為：如果已知不確定性因素R1、R2、R3服從的概率分布，對它們進行隨機抽樣，然后計算出所抽取樣本點的目標響應，通過對響應結果的分析，可以估計目標響應Y1的概率分布特征(均值、均方差等)[4]。

蒙特卡羅模擬的穩健性分析主要分為兩個步驟：一是抽樣，抽樣分為簡單隨機性抽樣和描述性抽樣，其中描述性抽樣將每個隨機變量的空間區域劃分成相等的概率子空間，讓每個隨機變量的子空間與其他隨機變量的子空間只結合1次，如圖2所示，其中假設x1、x2均服從正態分布；二是統計計算[9]。

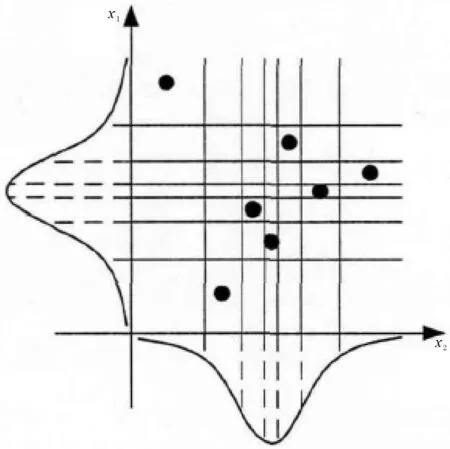
圖2　描述性抽樣示意

將抽樣值代入式(3)、式(4)，即可計算出目標函數的均值和均方差，計算公式如下：

(3)

(4)

式中：F為目標函數；xi為蒙特卡羅模擬樣本；N為樣本數；μ(F)和σ(F)為目標函數的均值和均方差[6]。

2　KCS船體型線特征參數穩健優化

以KCS船體型線為研究對象來驗證文中提及方法的有效性，采用Friendship軟件建立船體全參數化模型，基于Isight平臺實現船體型線特征參數穩健優化設計。

2.1KCS船體曲面全參數化建模

要實現船體型線的自動優化，首先必須以較少的特征參數建立參數化的船體幾何模型。通過船體參數化建模，可以將船體型線用有限的船體參數表達出來，通過控制這些參數來改變船體形狀，對這些參數進行篩選處理后可作為船型優化的變量，是船型優化的基礎性工作。

本研究中，利用參數化建模軟件Friendship進行船體參數化建模。首先根據船型選擇合適的船體特征參數，然后依據參數化設計技術，構建船體特征曲線，進而生成船體橫剖面，最后采用“蒙面法”生成光順曲面，即得到了船體參數化模型[10]。其具體過程見文獻[10]。

本文僅以船舯曲面建模為例簡單解釋其原理。首先必須要介紹FSpline曲線，它是一種經過光順處理的B樣條曲線，是Friendship船型參數化建模中很重要的一種曲線。該曲線可以由曲線起點坐標、終點坐標、起點切角、終點切角、曲線與坐標軸所圍面積及所圍面積區域的形心這6個參數來實現曲線的參數化表達。船舯橫剖面可由一段底部直線(bottom)、舭部曲線(bilge)和舷側直線段(side)組成，如圖3所示，其相關參數含義見表1。其輸入參數與特征曲線的對應關系如圖4所示，例如D點Z坐標為甲板高度值，其對應的縱向曲線為甲板邊線，C點Z坐標為舭部高度值，對應的縱向曲線為平邊線等。然后采用“蒙面法”生成光順曲面，可簡單理解為橫剖面沿著縱向曲線滑動，其掃過的曲面即為船體曲面。其中縱向曲線由FSpline曲線、直線或兩者組合構成，可通過船體特征參數控制縱向曲線的變化，進而改變船體形狀，即實現船體參數化，最終模型如圖5所示。

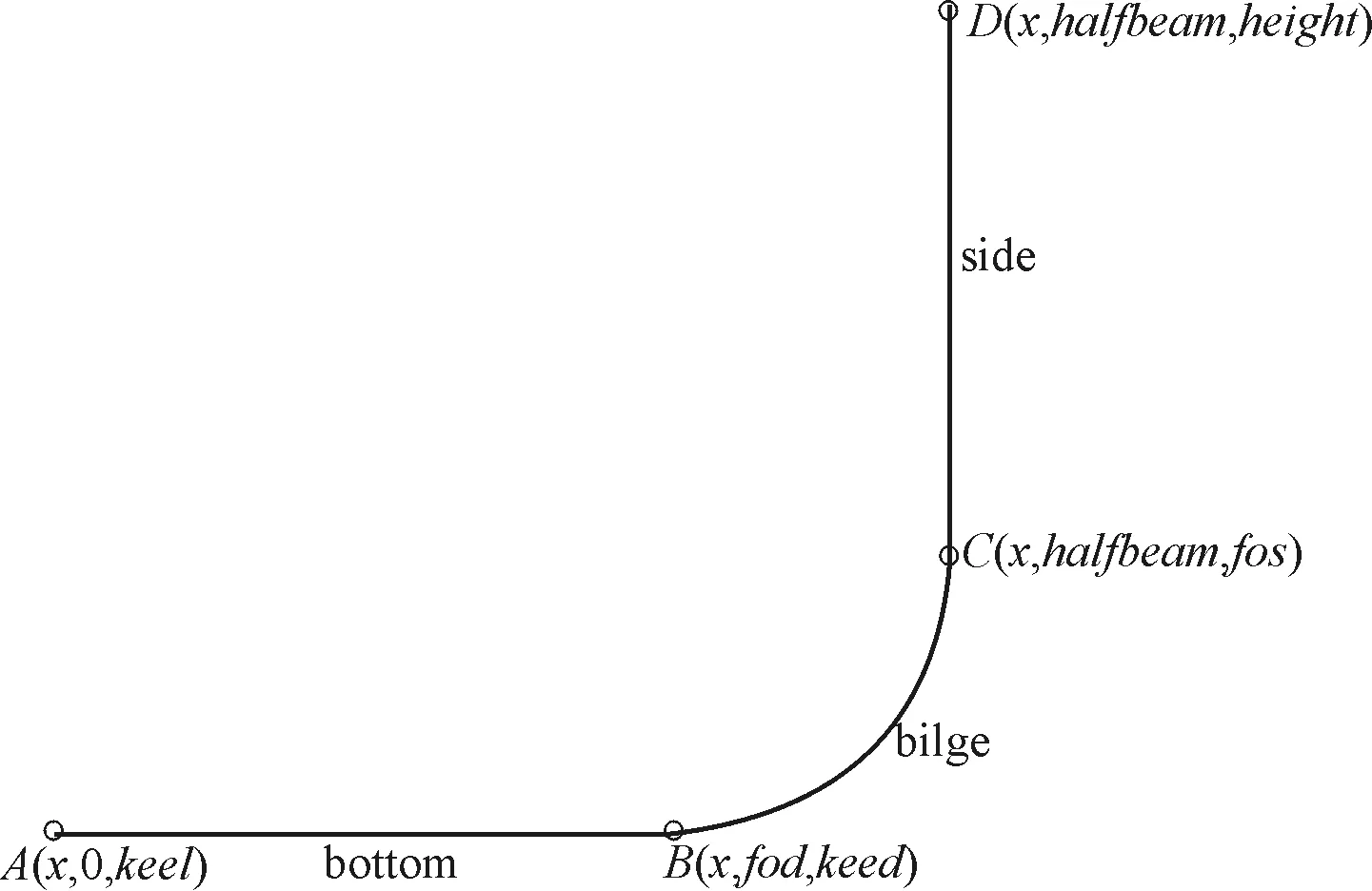
圖3　橫剖面形狀圖

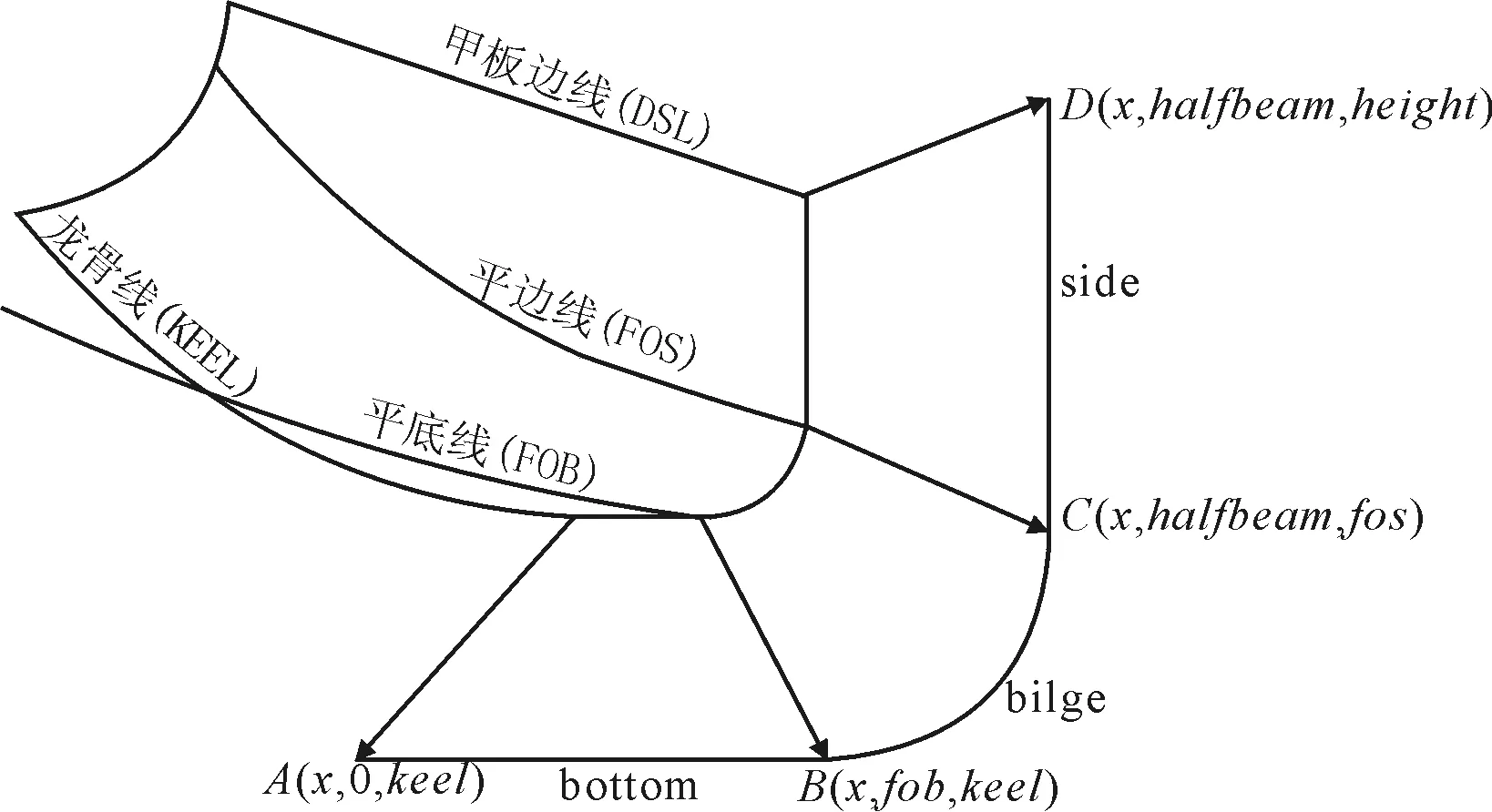
圖4　輸入參數與特征曲線對應關系

圖5　KCS船體模型

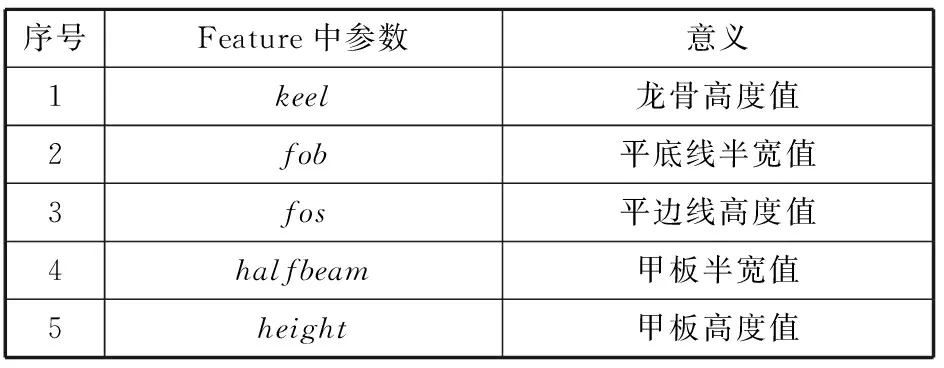
表1　相關參數列表

2.2優化變量

本研究選擇船體的舯前部為優化對象。由于球鼻艏對興波阻力影響顯著，選擇球鼻艏的全部參數作為變量，共18個，控制外飄角曲線的參數3個，控制舯前部橫剖面面積曲線的參數3個，控制水線形狀的參數2個，其相應的變化范圍見表2，變量控制部位如圖6所示。

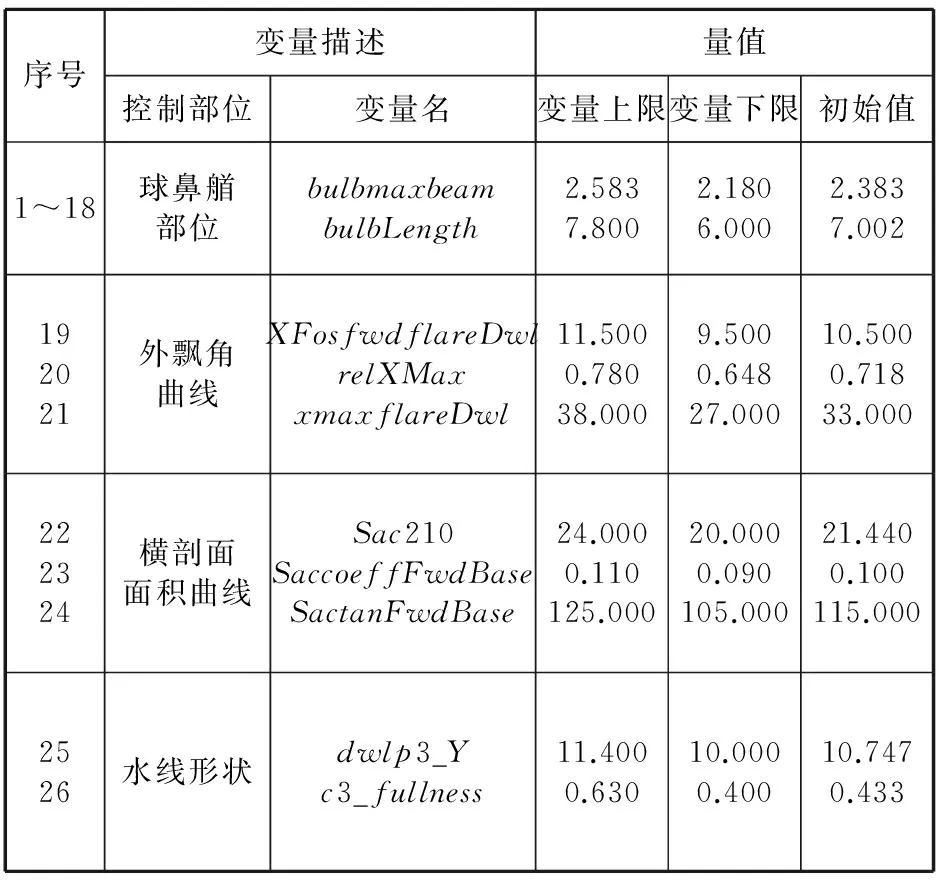
表2　設計變量定義

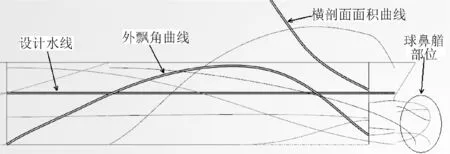
圖6　變量控制部位

2.3優化目標及約束條件

船舶在實際航行過程中，由于受到風、浪、流等因素的影響導致船舶的實際航速不會剛好是設計航速，而是在設計航速附近一定范圍內圍繞設計航速波動，在穩健優化中，近似認為它服從正態分布。

考慮船舶在實際航行中航速的波動，在CFD計算中，航速的改變通過改變傅氏數實現，其具體表達式為[11]：

Fractural=Frdesign+fr

(5)

式中：Fractural為實際傅氏數；Frdesign為設計傅氏數，Frdesign=0.26；fr為服從均值0、方差0.008的正態分布的不確定性變量。

本研究在考慮航速波動情況下，以減小船舶興波阻力系數的均值及均方差為目標進行優化。由于船體舯前部型線對于興波阻力影響顯著，因此本文重點對該區域線型進行優化。

約束條件滿足如下要求：

(1)排水量上下浮動小于1%。

(2)浮心縱向位置前后浮動小于1%。

該問題的確定性優化數學模型為：

minfobj

…

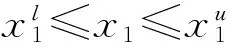
(6)

式中：fobj為優化目標函數，本文中指興波阻力系數；x1，x2…x26為表2中26個設計變量；g1為排水量；g2為浮心縱向位置；帶“l”上標的為參數下限值；帶“u”上標的為參數上限值。

相應的穩健優化數學模型為：

…

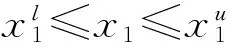
(7)

式中：W1和W2分別為興波阻力系數的平均值μ(fobj)和均方差σ(fobj)的權重系數，W1=W2=1；S1和S2分別為Y的平均值μ(fobj)和均方差σ(fobj)的歸一化系數，S1=1，S2=0.001。

在上述穩健優化數學模型中，由于約束條件(浮心縱向位置和排水量)對航速并不敏感，不會發生由于航速的波動導致超出約束條件，所以并沒有如式(1)中對約束條件進行調整，保持原約束條件不變。

2.4優化過程

整個優化過程在Isight集成平臺上實現，具體的流程如圖7所示。

(1)建立船體全參數化模型，使之可以通過改變船體特征參數來實現船型的變化。

(2)利用CFD-Shipflow進行計算，算出當前船型的興波阻力系數。

(3)假定傅氏數服從均值0、方差0.04的正態分布，利用蒙特卡羅模擬技術對傅氏數進行取樣，并對每個樣本點進行CFD計算，將結果代入式(3)、式(4)，計算出目標函數的均值及均方差。

(4)判斷是否滿足穩健優化準則，不滿足則按優化算法修改船型的特征參數，得到新船型后再次計算，直到滿足優化準則，輸出船體特征參數穩健優化組合。

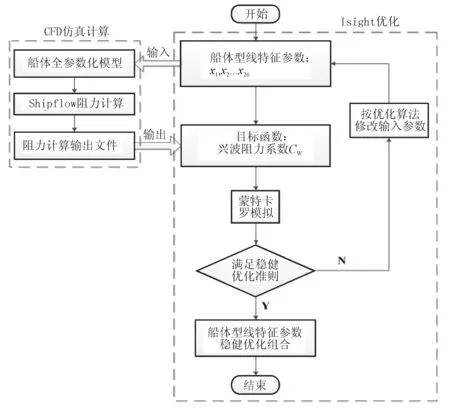
圖7　優化過程流程圖

2.5結果分析

確定性優化和穩健優化均采用遺傳算法NSGAⅡ作為優化算法，設計的優化種群數為50個，遺傳代數為20代，變異率為0.01，交叉率為0.9，優化結果見表3。確定性優化以興波阻力系數最小為目標，其優化數學模型見式(6)。初始設計和確定性優化方案的均值及方差均是假設傅氏數滿足同樣正態分布，通過蒙特卡羅模擬得到。確定性優化前后波形及船體型線對比如圖8、圖9所示，穩健優化前后波形及船體型線對比如圖10、圖11所示。圖8、圖10的縱向波切圖中，橫坐標為波高所在縱向位置，船首為0，船尾為1，縱坐標為波高值，均通過船長L進行無因次化。

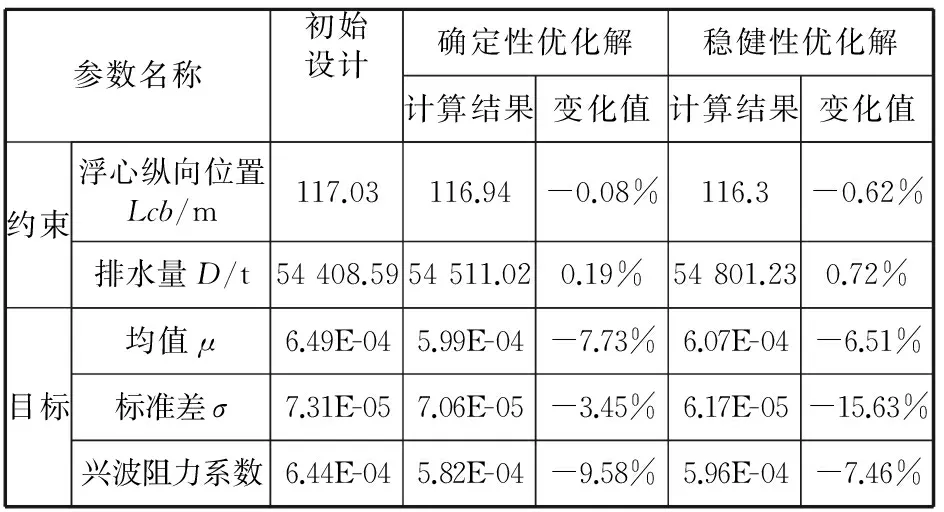
表3　優化結果

通過優化前后性能指標的對比發現，確定性優化后浮心縱向位置略微后移，興波阻力系數降低了9.58%。圖8表明優化船型的艏部波峰峰值比母型船有所降低，船體中后部波形基本相同，優化船型的自由液面波形較母型船有所簡化，從而降低了興波阻力。對比確定性優化前后船體型線可以發現，優化船型球艏形狀有一定變大且明顯上翹的趨勢，其圖形如圖9所示。

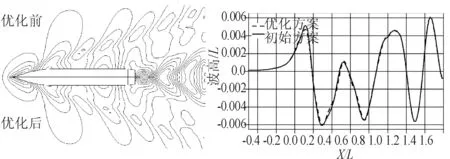
圖8　確定性優化前后波形輪廓圖、縱向波切圖對比

圖9　確定性優化前后型線對比

對比穩健優化前后船體型線可以發現，穩健優化方案與確定性優化方案的船型變化趨勢是一致的，球鼻艏形狀均有上翹的趨勢，穩健優化方案興波阻力系數降低了7.46%，較確定性優化結果稍差。同樣，穩健優化后船體艏部波峰峰值較母型船有所降低，船體中后部波形基本相同，優化船型興波波形較母型船有所簡化，與確定性優化結果一致。

從表3可以看出，穩健優化方案的興波阻力系數均值雖然比確定性優化方案稍大，但是其均方差明顯降低，說明穩健優化方案興波阻力的波動性更小。當船舶航速產生波動時，阻力性能不會有劇烈的變化，一直保持較為良好的阻力性能。為驗證船體型線特征參數穩健優化設計的效果，對比優化前后船舶興波阻力隨航速變化的情況，并進行分析。不同傅氏數下的興波阻力如圖12所示。

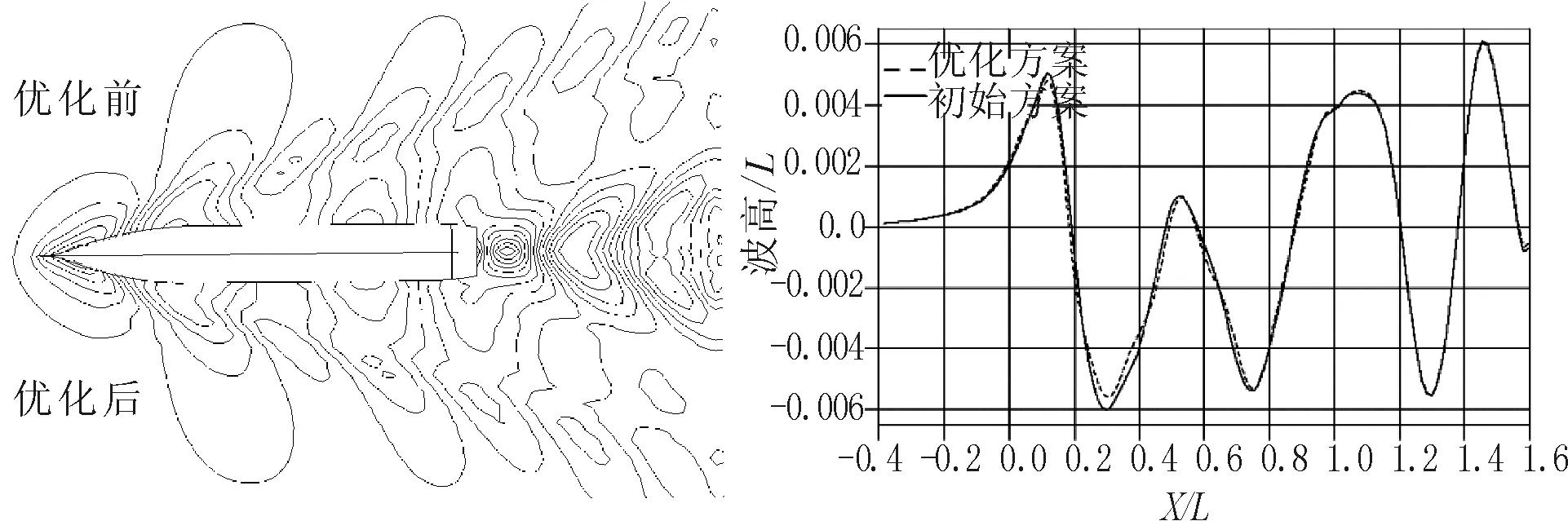
圖10　穩健優化前后波形輪廓圖、縱向波切圖對比

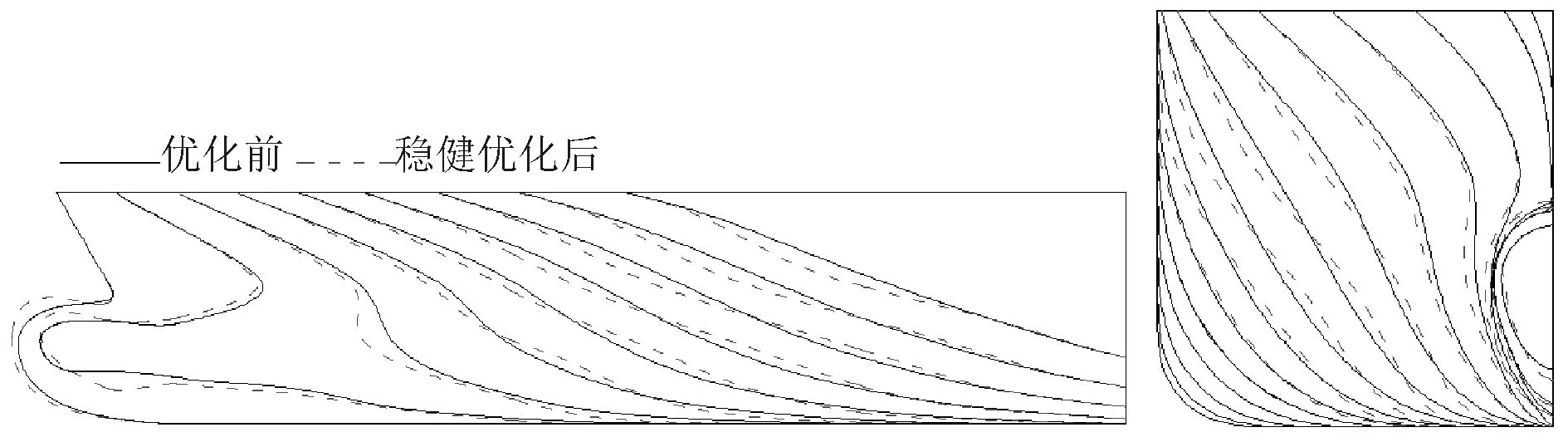
圖11　穩健優化前后型線對比

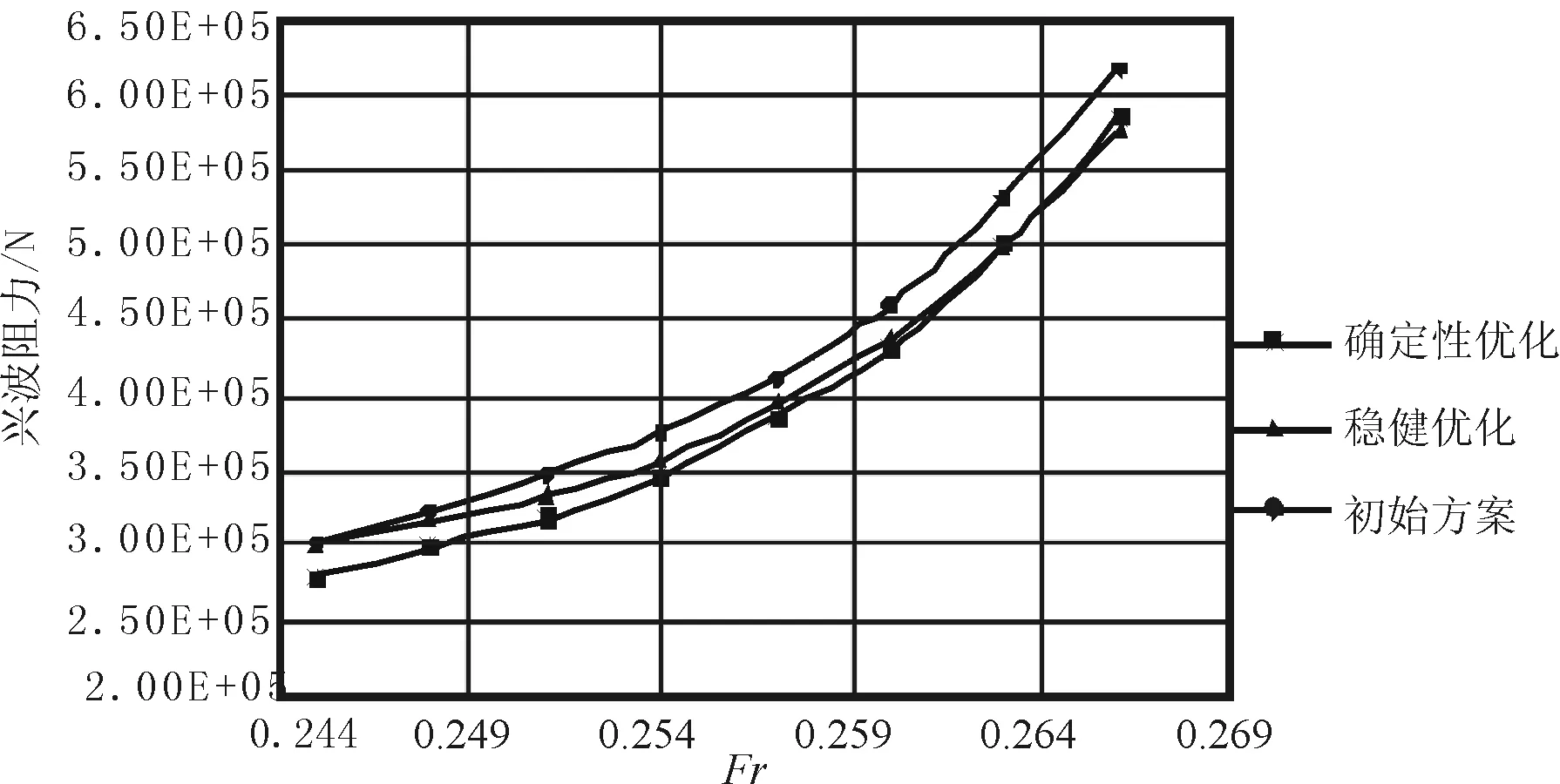
圖12　不同傅氏數下的興波阻力

從圖12可知，穩健優化方案在相同航速下的船舶興波阻力均比初始方案要小，且在整個速度范圍內波動幅度比初始方案及確定性優化方案小。上述分析說明，采用穩健優化設計得到的船型能夠在有效降低船舶阻力的同時，減小了阻力性能的波動，防止由于航速波動導致阻力性能惡化，使得優化方案失效，保證了船型優化的有效性。

3　結論

在船型優化過程中引入設計變量中的不確定性因素，運用基于蒙特卡羅模擬法的穩健優化設計方法，對KCS船進行了船體型線特征參數穩健優化設計研究，得到以下幾點結論：

(1)實際船型優化設計中存在各種不確定性因素，這些因素的波動會使得船型優化方案出現偏差甚至失效。因此，將穩健優化設計方法引入到船型優化中，對提高船型優化的工程實用性具有重要的研究意義。

(2)以KCS船為研究對象，考慮船舶在實際航行中存在的不確定性因素，應用基于蒙特卡羅模擬的穩健優化方法，得到的船型方案不僅優于母型船，而且與傳統確定性優化結果相比，方案的穩健性得到較大提高，保證了船型優化的有效性，證明了該優化方法在船型優化中的適用性。

[1]邵偉. 基于魯棒性的船舶結構優化設計研究[D]. 鎮江：江蘇科技大學, 2012.

[2]李冬琴, 蔣志勇, 趙欣. 多維隨機不確定性下的船舶多學科穩健設計優化研究[J]. 船舶工程, 2015, 37(11):61-66.

[3]Diez M, Peri D. Robust optimization for ship conceptual design[J]. Ocean Engineering, 2010, 37(11): 966-977.

[4]賴宇陽.Isight參數優化理論與實例詳解[M].北京:北京航空航天大學出版社,2012.

[5]孫光永, 李光耀, 陳濤, 等. 基于 6σ 的穩健優化設計在薄板沖壓成形中的應用[J]. 機械工程學報, 2008, 44(11): 248-254.

[6]王婷. 高速客車軸箱懸掛參數穩健優化設計[D]. 長沙:中南大學, 2014.

[7]李玉強, 崔振山, 陳軍, 等. 基于響應面模型的 6σ 穩健設計方法[J]. 上海交通大學學報, 2006, 40(2): 201-205.

[8]Nedjalkov M, Kosina H, Selberherr S. Monte Carlo algorithms for stationary device simulations[J]. Mathematics and Computers in Simulation, 2003, 62(3): 453-461.

[9]Yang R J, Gu L. Application of descriptive sampling and metamodeling methods for optimal design and robustness of vehicle structures[J]. AIAA, 2002, 1(321): 1-7.

[10]胡春平. 基于 Friendship 的船體型線優化技術研究[D]. 武漢: 武漢理工大學, 2012.

[11]Hannapel S E. Development of multidisciplinary design optimization algorithms for ship design under uncertainty[D]. Ann Arbor:The University of Michigan, 2012.

2016-03-12

國家自然科學基金項目(51279147, L1422029)

蔣國偉(1992—)，男，碩士研究生，從事船舶多學科設計優化技術研究；馮佰威(1974—)，男，副教授，從事計算機輔助船舶設計、船舶多學科設計優化技術研究；常海超(1985—)，男，講師，從事船舶多學科設計優化技術研究。

U662.2

A