一類特殊圖的兩種染色

李超，張東翰

（商洛學(xué)院數(shù)學(xué)與計(jì)算機(jī)應(yīng)用學(xué)院，陜西商洛　726000）

數(shù)學(xué)研究

一類特殊圖的兩種染色

李超，張東翰

（商洛學(xué)院數(shù)學(xué)與計(jì)算機(jī)應(yīng)用學(xué)院，陜西商洛726000）

利用窮舉法和組合分析法討論了一類特殊圖的鄰強(qiáng)邊染色和鄰點(diǎn)可區(qū)別的全染色，通過構(gòu)造具體染色得到了該類圖的鄰強(qiáng)邊色數(shù)和鄰點(diǎn)可區(qū)別的全色數(shù)。

窮舉法；鄰強(qiáng)邊染色；鄰點(diǎn)可區(qū)別的全染色

圖的染色是圖論的主要研究內(nèi)容之一，很多人對其進(jìn)行了研究，文獻(xiàn)［1］給出了圖的鄰強(qiáng)邊染色的概念和一些特殊圖的具體染色，文獻(xiàn)［2-3］通過構(gòu)造具體染色得到了一些特殊圖的鄰強(qiáng)邊染色數(shù)，文獻(xiàn)［4］給出了鄰點(diǎn)可區(qū)別的全染色的概念和若干特殊圖的染色，文獻(xiàn)［5-6］給出了若干特殊圖的鄰點(diǎn)可區(qū)別的全色數(shù)。本文將研究一類特殊圖的鄰強(qiáng)邊染色和鄰點(diǎn)可區(qū)別的全染色。

1　預(yù)備知識

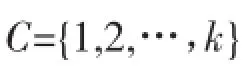
定義2［4-6］設(shè)G（V，E）是簡單圖，k是自然數(shù)，f是從V（G）∪E（G）到C=｛1，2，…，k｝的映射，如果滿足：

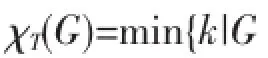
如果f是一個(gè)k正常全染色，并且滿足

定義3［7］由2個(gè)回路Cn恰有一個(gè)公共點(diǎn)所組成的圖記作D2，n，

其中，點(diǎn)集V（D2，n）=｛v0，v1，…，vn-1，u1，u2，…，un-1｝，邊集E（D2，n）=｛v0v1，v1v2，…，vn-1v0，v0u1，u1u2，…，un-1，un-2un-1，un-1v0｝

引理1［1-3］對于簡單圖G，有Δ≤χ′as（G）；若G有相鄰的兩個(gè)最大度點(diǎn)，則有Δ+1≤χ′as（G），其中Δ代表圖G的最大度。

引理2［4-6］對于簡單圖G，有Δ+1≤χ′at（G）；若G有相鄰的兩個(gè)最大度點(diǎn)，則有Δ+2≤χ′at（G），其中Δ代表圖G的最大度。

本文中未加敘述的術(shù)語、記號可在文獻(xiàn)［8-10］中找到。

2　定理及其證明

定理1 對于圖D2，n（n≥3），有χ′as（D2，n）=4。

證明 由于沒有相鄰的最大度點(diǎn)，所以根據(jù)引理1可知χ′as（D2，n）≥4，現(xiàn)給出一個(gè)4-ASEC，設(shè)色集合C=｛1，2，3，4｝。對于邊v0v1，v1v2，v2v3，…，vn-2vn-1分別用色1，3，4循環(huán)染，對于邊vn-1v0用色2染；對于邊v0u1，u1u2，u2u3，…，un-2un-1分別用色3，1，2循環(huán)染，對于邊un-1v0用色4染，則此染色法顯然是一個(gè)4-ASEC，即χ′as（D2，n）=4。……