關于近似R-正交的注記
2016-08-13 12:40:27孔亮王念良
商洛學院學報
2016年4期
關鍵詞:定義
孔亮,王念良
(商洛學院 數學與計算機應用學院,陜西商洛 726000)
關于近似R-正交的注記
孔亮,王念良
(商洛學院 數學與計算機應用學院,陜西商洛726000)
在復賦范線性空間,利用范數導數的定義和性質,并運用算子論方法,證明了近似R-正交是近似ρ-正交,給出了弱近似R-正交的定義,并證明了在一定條件下,近似ρ-正交是弱近似R-正交。
R-正交;近似R-正交;弱近似R-正交;近似正交
在20世紀初,R-正交、B-正交、I-正交等正交性定義被相繼引入用來研究賦范線性空間的幾何性質[1-3]。此后,新的正交性定義被不斷引入和研究,比如文獻[4]在Banach空間中給出新的正交性定義,文獻[5-6]引入了ρ-正交定義。近年來,許多學者推廣了以上正交性定義得到相應的近似正交性定義。文獻[7-8]在復賦范線性空間中給出了近似B-正交的定義和性質,文獻[9-10]在實賦范線性空間中分別引入了近似I-正交和近似R-正交的定義,關于其它各種正交性和近似正交性定義和相關性質已有許多研究[11-16]。受上述定義和結論的啟發,本文在復賦范線性空間,證明近似R-正交是近似ρ-正交,給出弱近似R-正交的定義,并證明在一定條件下,近似ρ-正交是弱近似R-正交。
1 預備知識和結論
X在本文中均表示復賦范線性空間,R表示實數集,C表示復數集,U(0;δ)表示在復平面上以原點為中心,以δ>0為半徑的鄰域。
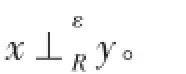
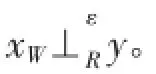
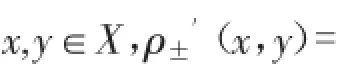
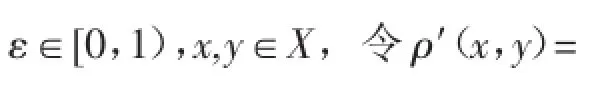
文獻[16]在復賦范線性空間中給出了范數導數的性質。
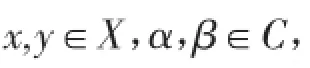
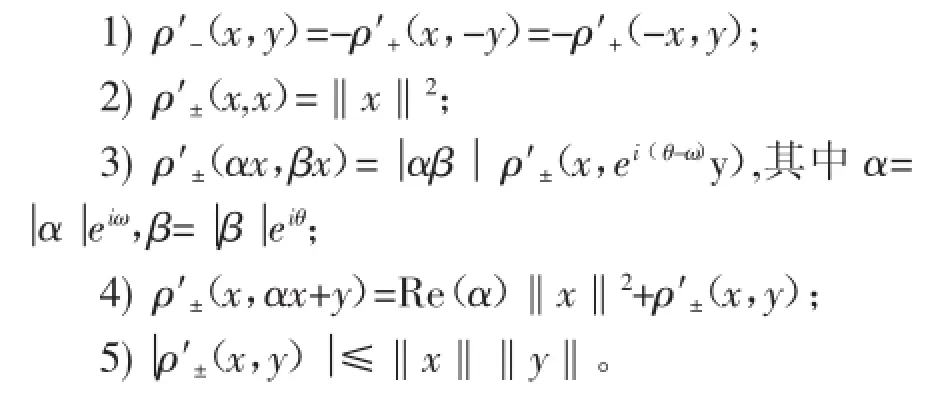
本文利用定義3和定理1,主要得到下面的結論。
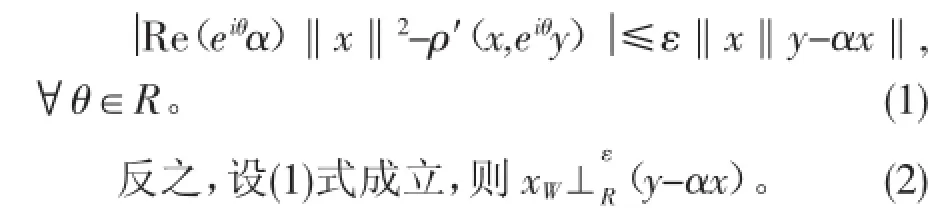
2 結論的證明
為了完成定理2的證明,先給出下面的引理。……
登錄APP查看全文
猜你喜歡
中學生數理化(高中版.高考數學)(2021年3期)2021-06-09 06:09:14
中學生數理化(高中版.高二數學)(2021年12期)2021-04-26 07:43:38
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:04
海峽姐妹(2020年9期)2021-01-04 01:35:44
華人時刊(2020年13期)2020-09-25 08:21:32
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
山東青年(2016年1期)2016-02-28 14:25:25
汽車維護與修理(2015年6期)2015-02-28 12:16:55
當代修辭學(2014年3期)2014-01-21 02:30:44
公務員文萃(2013年5期)2013-03-11 16:08:37

