基于組合預(yù)測模型的廣東省第三產(chǎn)業(yè)產(chǎn)值預(yù)測
葉藝勇


摘要首先分析了影響廣東省第三產(chǎn)業(yè)發(fā)展的主要因素,指出由于上述因素相互制約、相互影響,導(dǎo)致第三產(chǎn)業(yè)的發(fā)展呈現(xiàn)出高度的非線性特征,并使得單一的預(yù)測模型在預(yù)測效果和泛化能力方面難以勝任.在此基礎(chǔ)上,提出了基于神經(jīng)網(wǎng)絡(luò)集成的組合預(yù)測模型,對廣東省第三產(chǎn)業(yè)的發(fā)展進(jìn)行預(yù)測,闡述了算法的基本原理和數(shù)據(jù)處理流程,實(shí)證分析表明:基于神經(jīng)網(wǎng)絡(luò)集成的組合預(yù)測模型要比單一預(yù)測模型的預(yù)測精度高.
關(guān)鍵詞第三產(chǎn)業(yè),核方法,組合預(yù)測,支持向量回歸,神經(jīng)網(wǎng)絡(luò)
中圖分類號N945.12 文獻(xiàn)標(biāo)識碼A
AbstractThis paper analyzed the main factors on the improvement of tertiary industry, and pointed out that the single forecast model was difficult to satisfy the need of economic forecasting as the factors restrict and influence each other. On this basis, we proposed the combination forecasting model based on neural network ensemble, forecasted the development of tertiary industry of Guangdong Province, and described the basic principles and data processing algorithms. The empirical analysis shows that the combination forecasting model based on neural network ensemble has high prediction accuracy than a single forecast model.
Key wordstertiary industry; kernel method; forecast model; support vector regression; neural network ensemble
1引言
第三產(chǎn)業(yè)是指對消費(fèi)者提供最終服務(wù)和對生產(chǎn)者提供中間服務(wù)的行業(yè),除了第一、第二產(chǎn)業(yè)以外,其他所有的行業(yè)均屬于第三產(chǎn)業(yè).隨著社會經(jīng)濟(jì)的發(fā)展和國家對產(chǎn)業(yè)結(jié)構(gòu)的調(diào)整,第三產(chǎn)業(yè)的地位和重要性日益突出,以市場經(jīng)濟(jì)發(fā)達(dá)的廣東省為例,2013年,47.76%的生產(chǎn)總值是由第三產(chǎn)業(yè)貢獻(xiàn)的,遠(yuǎn)遠(yuǎn)超出第一產(chǎn)業(yè)的4.9%,略高于第二產(chǎn)業(yè)的47.34%,從以上數(shù)據(jù)可以看出,第三產(chǎn)業(yè)已經(jīng)成為廣東經(jīng)濟(jì)發(fā)展的主要推動力,加快發(fā)展第三產(chǎn)業(yè)既可以有效地推進(jìn)我國工業(yè)化和現(xiàn)代化的進(jìn)程,擴(kuò)大就業(yè)領(lǐng)域和就業(yè)人數(shù),還可以保證社會安定,提高人民生活水平,改善生活質(zhì)量.
因此,深入研究第三產(chǎn)業(yè)的發(fā)展?fàn)顩r,對第三產(chǎn)業(yè)未來的發(fā)展有著重要的指導(dǎo)意義.要考察第三產(chǎn)業(yè)的發(fā)展,必須從全局的角度出發(fā)進(jìn)行分析,研究它的規(guī)律和發(fā)展趨勢,其中第三產(chǎn)業(yè)生產(chǎn)總值作為衡量第三產(chǎn)業(yè)發(fā)展?fàn)顩r的重要指標(biāo)之一,對其進(jìn)行科學(xué)的分析和預(yù)測,能為第三產(chǎn)業(yè)的發(fā)展和政策的制定提供有力的參考依據(jù).
圖1是廣東省1987~2013年三大產(chǎn)業(yè)產(chǎn)值比例變化圖,從圖1可知:第一產(chǎn)業(yè)所占的比重迅速下降,第二產(chǎn)業(yè)的比重穩(wěn)中有升,而第三產(chǎn)業(yè)的比重增加最快,但從圖2可知,廣東省第三產(chǎn)業(yè)生產(chǎn)總值的增長是呈現(xiàn)非線性狀態(tài)的,這是由于反映經(jīng)濟(jì)發(fā)展的各項指標(biāo)互相聯(lián)系、互相作用所導(dǎo)致的,特別是由于經(jīng)濟(jì)系統(tǒng)自身的復(fù)雜性和動態(tài)性,使得指標(biāo)數(shù)據(jù)呈現(xiàn)高度的非線性、非精確性等特征.因此,要實(shí)現(xiàn)對廣東省第三產(chǎn)業(yè)生產(chǎn)總值的準(zhǔn)確預(yù)測,必須要解決兩方面的問題,一方面是預(yù)測指標(biāo)體系的構(gòu)建要全面反映第三產(chǎn)業(yè)發(fā)展的基本情況,另一方面是選擇合適的預(yù)測方法對樣本數(shù)據(jù)進(jìn)行模擬仿真.
2文獻(xiàn)綜述
當(dāng)前已有眾多學(xué)者對第三產(chǎn)業(yè)的發(fā)展進(jìn)行了深入的研究.使用的方法包括灰色理論、神經(jīng)網(wǎng)絡(luò)、ARIMA模型、逐步回歸分析等,并取得了一定的成效.如崔二濤等利用二次曲線指數(shù)平滑模型對廈門市第三產(chǎn)業(yè)的增加值進(jìn)行預(yù)測研究,獲得了較為精準(zhǔn)的預(yù)測效果[1];呂一清等研究了基于灰色神經(jīng)網(wǎng)絡(luò)的第三產(chǎn)業(yè)發(fā)展趨勢的預(yù)測模型,實(shí)證分析表明灰色神經(jīng)網(wǎng)絡(luò)比單一的灰色預(yù)測模型和傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型擬合和預(yù)測能力要好,適合應(yīng)用于成都第三產(chǎn)業(yè)發(fā)展趨勢的預(yù)測[2];徐群等將主成分分析和逐步回歸分析應(yīng)用于我國第三產(chǎn)業(yè)發(fā)展現(xiàn)狀研究及趨勢預(yù)測,并對如何保持我國第三產(chǎn)業(yè)穩(wěn)步發(fā)展給出合理化建議[3];鄧偉使用ARIMA模型對廣東省第三產(chǎn)業(yè)的發(fā)展情況進(jìn)行短期預(yù)測,實(shí)證檢驗(yàn)發(fā)現(xiàn):模型的預(yù)測誤差較小,預(yù)測精度較高[4];李榮麗等則研究了將時間序列BP神經(jīng)網(wǎng)絡(luò)應(yīng)用于福州市第三產(chǎn)業(yè)值的預(yù)測,研究結(jié)果表明:BP神經(jīng)網(wǎng)絡(luò)模型收斂速度較快,預(yù)測精度較高,具有較高的應(yīng)用價值[5].
上述研究成果的特點(diǎn)是將單一的模型應(yīng)用于第三產(chǎn)業(yè)的發(fā)展預(yù)測,但由于每個模型均有自身的局限性,導(dǎo)致在實(shí)踐中,對同一個問題,采用不同的預(yù)測方法會產(chǎn)生不同的預(yù)測結(jié)果,即存在預(yù)測精度的差異.因?yàn)槊恳环N預(yù)測方法都不可能做到零誤差,但是不同的方法往往又能提供不同角度的有效信息,因此,單一預(yù)測模型在預(yù)測結(jié)果的準(zhǔn)確性和信息反映的全面性、以及模型的泛化能力方面均存在一定的缺陷,考慮使用組合預(yù)測模型的方法來改善單一模型的不足,因?yàn)榻M合預(yù)測模型能夠較大限度地利用樣本的各種信息,比單個模型考慮問題更加系統(tǒng)、全面,能夠有效地減少預(yù)測過程中隨機(jī)因素的影響程度,避免在面對復(fù)雜系統(tǒng)時出現(xiàn)預(yù)測偏差波動較大,泛化能力不足的情況,從而提高預(yù)測的精度與模型的穩(wěn)定性.
3廣東省第三產(chǎn)業(yè)發(fā)展影響因素分析
第三產(chǎn)業(yè)作為國民經(jīng)濟(jì)一個重要的組成部分,它的發(fā)展受到多方面因素的制約,這些因素相互聯(lián)系、互相滲透,共同影響著第三產(chǎn)業(yè)的發(fā)展水平和發(fā)展速度,本文遵循可獲得性、可比性、客觀性、綜合性的原則,結(jié)合定性和定量的相關(guān)性分析,以及參考其他學(xué)者的研究成果[6-8],認(rèn)為以下幾個方面與廣東省第三產(chǎn)業(yè)生產(chǎn)總值的變化相關(guān)性最大.
1)人均生產(chǎn)總值
人均GDP反映了一個地區(qū)的經(jīng)濟(jì)總體發(fā)展水平,人均GDP的增長會引起社會需求結(jié)構(gòu)的相應(yīng)變化,與之相關(guān)的是,各產(chǎn)業(yè)產(chǎn)品的需求收入也會彈性地發(fā)生變化,從而引起各產(chǎn)業(yè)在經(jīng)濟(jì)發(fā)展中的地位發(fā)生改變,最終導(dǎo)致產(chǎn)業(yè)結(jié)構(gòu)的變化.
2)城鎮(zhèn)居民可支配收入
一個地區(qū)居民的消費(fèi)水平與該地區(qū)第三產(chǎn)業(yè)的發(fā)展水平是密切相關(guān)的.城鄉(xiāng)居民消費(fèi)帶動了城市第三產(chǎn)業(yè)的發(fā)展,其消費(fèi)水平越高,第三產(chǎn)業(yè)的發(fā)展就越迅速,第三產(chǎn)業(yè)產(chǎn)值占國民收入總額的比例也越大.一個地區(qū)居民的消費(fèi)水平可以用城鎮(zhèn)居民可支配收入指標(biāo)來衡量.
3)固定資產(chǎn)投資
固定資產(chǎn)投資是衡量經(jīng)濟(jì)發(fā)展水平的重要指標(biāo),固定資產(chǎn)投資額的增加會加強(qiáng)區(qū)域的水利、電力、能源、通訊、城鄉(xiāng)公用設(shè)施等基礎(chǔ)建設(shè), 從而帶動地質(zhì)勘察、水利管理、交通運(yùn)輸、倉儲及郵電、房地產(chǎn)業(yè)等第三產(chǎn)業(yè)的產(chǎn)值增加,加大其投資力度能消除經(jīng)濟(jì)發(fā)展中的“瓶頸 ”問題,因此, 固定資產(chǎn)投資作為模型的一個輸入變量.
4)第三產(chǎn)業(yè)就業(yè)人數(shù)
第三產(chǎn)業(yè)的快速發(fā)展能廣泛地吸收勞動力資源,因此第三產(chǎn)業(yè)的就業(yè)人數(shù)在一定程度上能夠反映第三產(chǎn)業(yè)的發(fā)展?fàn)顩r;而就業(yè)人員的素質(zhì),將在很大程度上決定了第三產(chǎn)業(yè)發(fā)展的進(jìn)程和行業(yè)經(jīng)營的狀況,高素質(zhì)的人力資源能夠促使第三產(chǎn)業(yè)的快速健康發(fā)展.
5)城市化水平
城市化水平是指一個地區(qū)農(nóng)村向城市發(fā)展的狀況,通常代表著該地區(qū)經(jīng)濟(jì)的發(fā)展水平.城市經(jīng)濟(jì)的發(fā)展,吸引了大量農(nóng)村剩余勞動力的涌入,產(chǎn)生了很強(qiáng)的規(guī)模經(jīng)濟(jì)效應(yīng).城市經(jīng)濟(jì)聚集性、開放性等特點(diǎn)為第三產(chǎn)業(yè)發(fā)展創(chuàng)造了良好的條件.因此,要想實(shí)現(xiàn)第三產(chǎn)業(yè)發(fā)展,需要努力提高地區(qū)的城市化水平.
6)外貿(mào)出口總額
服務(wù)產(chǎn)品的輸出狀況會影響一個區(qū)域的第三產(chǎn)業(yè)結(jié)構(gòu).因?yàn)樵谳敵錾唐返耐瑫r,也是運(yùn)輸、信息、科技等服務(wù)的對外輸出.此外,出口的產(chǎn)值將會對第三產(chǎn)業(yè)行業(yè)的結(jié)構(gòu)產(chǎn)生影響,此結(jié)論也是被很多經(jīng)濟(jì)學(xué)家認(rèn)同的,所以本文中也引進(jìn)外貿(mào)出口總額作為輸入指標(biāo).
綜上所述,最終確定預(yù)測模型的輸入指標(biāo)是:廣東省人均GDP,城鎮(zhèn)居民可支配收入,固定資產(chǎn)投資,第三產(chǎn)業(yè)就業(yè)人數(shù),城市化水平,外貿(mào)出口總額,預(yù)測對象為廣東省第三產(chǎn)業(yè)生產(chǎn)總值.
3基于神經(jīng)網(wǎng)絡(luò)的組合預(yù)測模型
3.1支持向量回歸模型
由統(tǒng)計學(xué)習(xí)理論發(fā)展而成的核方法,是一類模式識別的算法,其目的是找出并學(xué)習(xí)一組數(shù)據(jù)中的相互關(guān)系,它是解決非線性模式分析問題的一種有效途徑.SVR,即支持向量回歸,是目前核方法應(yīng)用的經(jīng)典模型,它對非線性、非確定性、非精確性數(shù)據(jù)的擬合能力表現(xiàn)非常優(yōu)秀,在復(fù)雜的非線性預(yù)測以及綜合評價中有著非常的廣泛應(yīng)用前景[9].更加重要的是,SVR是建立在結(jié)構(gòu)風(fēng)險最小化的優(yōu)化目標(biāo)上,它可以在過度學(xué)習(xí)和模型適應(yīng)性之間取得很好的平衡,在很大程度上改善了其他智能算法在非線性擬合上存在的不足.
從本質(zhì)上講,線性多元回歸就是求方程[10]:
y=Xw+ε.(1)
考慮到對回歸曲線本身的要求,在如圖3所示的ε不敏感損失函數(shù)下,線性回歸問題可轉(zhuǎn)化為優(yōu)化問題:
3.2約束條件下的線性回歸模型
在現(xiàn)實(shí)問題研究中,因變量的變化往往受幾個重要因素的影響,此時就需要用2個或2個以上的影響因素作為自變量來解釋因變量的變化,這就是多元回歸亦稱多重回歸.當(dāng)多個自變量與因變量之間是線性關(guān)系時,所進(jìn)行的回歸分析就是多元線性回歸.約束條件下的線性多元回歸模型(簡稱為CMVR模型)[11],可描述為:
y=Xβ+ε,lb≤β≤ub.(8)
其中,lb,ub分別為β的上下限.
其中,式(8)可轉(zhuǎn)化為如下的求優(yōu)化問題:
min Q=(y-Xβ)2,s.t.lb<β 其中,y,X,β分別為n×1,n×m,m×1矩陣. 3.3擴(kuò)展CobbDouglas生產(chǎn)函數(shù)模型 柯布道格拉斯生產(chǎn)函數(shù)是美國數(shù)學(xué)家柯布(C.W.Cobb)和經(jīng)濟(jì)學(xué)家保羅·道格拉斯(PaulH.Douglas)共同探討投入和產(chǎn)出的關(guān)系時創(chuàng)造的生產(chǎn)函數(shù),是用來預(yù)測國家和地區(qū)的工業(yè)系統(tǒng)或大企業(yè)生產(chǎn)一種經(jīng)濟(jì)數(shù)學(xué)模型,簡稱生產(chǎn)函數(shù),它是經(jīng)濟(jì)學(xué)中使用最廣泛的一種生產(chǎn)函數(shù)形式,在數(shù)理經(jīng)濟(jì)學(xué)與經(jīng)濟(jì)計量學(xué)的研究與應(yīng)用中都具有非常重要的地位[11]. ECDPF即擴(kuò)展的CobbDouglas生產(chǎn)函數(shù),該模型可描述為:設(shè)y為第三產(chǎn)業(yè)生產(chǎn)總值,xi為與之相關(guān)聯(lián)指標(biāo)的數(shù)值,αi為與xi相對應(yīng)的指數(shù),則: y=α0∏ixαii+ε.(10) 兩邊取對數(shù),有: ln y=ln α0+∑iαiln xi+ε0.(11) 同樣具有約束條件:αi>0.(12) 3.4基于神經(jīng)網(wǎng)絡(luò)的組合預(yù)測模型 由于單個模型預(yù)測存在一定的不足之處,因此,本文使用組合預(yù)測模型的方法來完成數(shù)據(jù)的建模與仿真.目前,關(guān)于組合預(yù)測的研究,主要集中在3個方面,一是關(guān)于預(yù)測信息的組合,二是預(yù)測方法的組合,三是預(yù)測結(jié)果的組合.本文主要是針對單個模型的預(yù)測結(jié)果進(jìn)行組合,其中的關(guān)鍵步驟就是尋找用于組合各單項模型預(yù)測結(jié)果的權(quán)系數(shù).現(xiàn)有的組合預(yù)測處理方法大部分是限于定權(quán)系數(shù),即對于第i種預(yù)測方法,其加權(quán)系數(shù)Ki是固定的,與時間、外部環(huán)境等因素?zé)o關(guān),這顯然是不科學(xué)的.因?yàn)楦鞣N預(yù)測方法對于不同的預(yù)測時間段表現(xiàn)出不同的預(yù)測能力:有的方法對瞬態(tài)變化敏感,適用于短期預(yù)測;有的方法善于把握長期趨勢,表現(xiàn)出優(yōu)越的中長期預(yù)測能力.如果將不同時間組合的權(quán)系數(shù)設(shè)定為常值,就無法各取所長,獲得最佳預(yù)測結(jié)果.
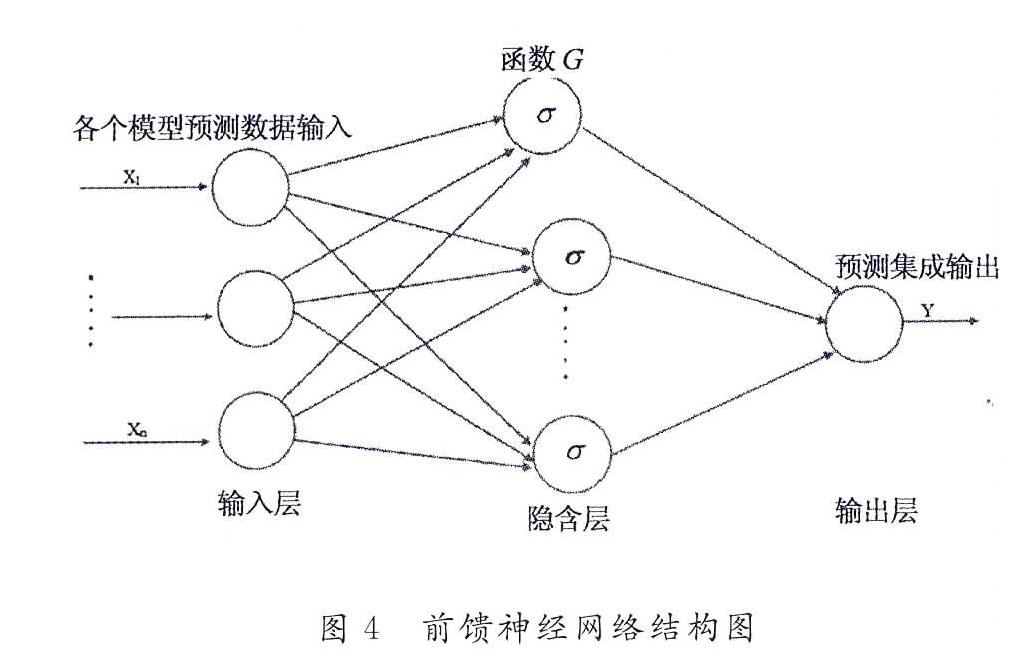
鑒于變權(quán)重的組合預(yù)測方法是提高模型的擬合精度和預(yù)測精度、增強(qiáng)預(yù)測模型實(shí)用性的有效手段.本文提出使用神經(jīng)網(wǎng)絡(luò)來集成各個模型的輸出,因?yàn)閺睦碚撋现v,一個具有Sigmoid函數(shù)的三層前饋神經(jīng)網(wǎng)絡(luò)能夠擬合任意非線性函數(shù)[12].神經(jīng)網(wǎng)絡(luò)的實(shí)質(zhì)就是一個從輸入層到輸出層的非線性映射,它的訓(xùn)練過程實(shí)際上就是一個優(yōu)化計算的過程.如果以各個模型的預(yù)測數(shù)據(jù)作為輸入,以待預(yù)測序列的真實(shí)值作為理想輸出來訓(xùn)練神經(jīng)網(wǎng)絡(luò),則其訓(xùn)練過程就是尋找最優(yōu)的權(quán)值,使得組合預(yù)測的誤差平方和達(dá)到最小的過程,這實(shí)際上就實(shí)現(xiàn)了組合預(yù)測的最優(yōu)組合.神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)如圖4所示.
因此,基于神經(jīng)網(wǎng)絡(luò)集成的組合預(yù)測模型,其數(shù)據(jù)處理的基本原理是:將各個模型訓(xùn)練階段的預(yù)測數(shù)據(jù)作為神經(jīng)網(wǎng)絡(luò)的輸入,訓(xùn)練階段的實(shí)際數(shù)據(jù)作為輸出,構(gòu)建神經(jīng)網(wǎng)絡(luò)模型,即該模型具有n個輸入變量(假設(shè)有n個預(yù)測模型),1個輸出變量的結(jié)構(gòu),由訓(xùn)練階段的數(shù)據(jù)確定模型最佳參數(shù);第二步,將測試階段各個模型的預(yù)測數(shù)據(jù)作為訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)模型的輸入,計算其輸出,即為組合預(yù)測模型的輸出結(jié)果.
4實(shí)證研究
4.1數(shù)據(jù)預(yù)處理及模型訓(xùn)練
本文所有經(jīng)濟(jì)數(shù)據(jù)均來源于廣東省統(tǒng)計年鑒(1987~2014年).
由于不同指標(biāo)的單位不一致,為了提高預(yù)測的精度,也為了消除不同年份價格指數(shù)差異所帶來的影響,使不同年份的數(shù)據(jù)具有可比性,在使用模型處理數(shù)據(jù)之前,首先把原始數(shù)據(jù)轉(zhuǎn)化為環(huán)比數(shù)據(jù),轉(zhuǎn)換公式如下:
X當(dāng)前年份=Y當(dāng)前年份/W當(dāng)前年份Y上一年度/W上一年度.(13)
式中:X為指標(biāo)的環(huán)比數(shù)據(jù),Y為指標(biāo)的純量數(shù)據(jù),W為累計物價指數(shù).
由于經(jīng)濟(jì)發(fā)展具有一定的延續(xù)性和滯后性,因此,在實(shí)際的經(jīng)濟(jì)系統(tǒng)運(yùn)行過程中,近期的經(jīng)濟(jì)數(shù)據(jù)對未來的影響比早期的數(shù)據(jù)應(yīng)該更大,為了體現(xiàn)對近期數(shù)據(jù)的重視程度,把1987~2008年22個年度的數(shù)據(jù)樣本按1.2的比例加權(quán)作為學(xué)習(xí)樣本,對模型進(jìn)行訓(xùn)練,以確定各模型的參數(shù)值,然后將2009~2013年的數(shù)據(jù)作為測試樣本,用于檢驗(yàn)?zāi)P偷念A(yù)測效果.
4.2模型測試
4.2.1單個模型預(yù)測
分別使用上述3個訓(xùn)練好的模型對測試樣本數(shù)據(jù)進(jìn)行擬合,得到的結(jié)果如表1所示.
從表1可知,3個模型的平均預(yù)測誤差分別為5.68%,5.92%和3.77%,其中SVR模型的預(yù)測效果略比其他2個模型高.為了便于比較,將3個模型的預(yù)測輸出使用平均組合法處理,得到相應(yīng)的預(yù)測結(jié)果及誤差,如表1最后2列所示,可以看到,5年的平均預(yù)測誤差為5.12%,說明了簡單的組合預(yù)測效果在當(dāng)前的參數(shù)狀態(tài)下是可行的,但是由于平均組合法是忽略了各個模型之間的差異性,以同等的權(quán)重衡量各個模型的計算精度和重要性,從理論上來講,平均權(quán)重?zé)o法保證一定能獲得最優(yōu)的處理結(jié)果,權(quán)重相同只是眾多情況下的一種特殊選擇,因此,本文繼續(xù)使用基于神經(jīng)網(wǎng)絡(luò)集成的組合預(yù)測模型來改善預(yù)測精度.
4.2.2神經(jīng)網(wǎng)絡(luò)組合預(yù)測模型
根據(jù)神經(jīng)網(wǎng)絡(luò)組合預(yù)測的基本原理,該模型的輸入變量個數(shù)為3,輸出變量個數(shù)為1,關(guān)于隱含層的數(shù)量,設(shè)置其范圍初始區(qū)間為[4,10],通過訓(xùn)練樣本數(shù)據(jù)循環(huán)計算并比較,確定最佳的隱含層單元數(shù)為5,然后將3個模型的預(yù)測結(jié)果使用訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)模型集成輸出,結(jié)果如表2最后2列所示.
從表2可知,與平均組合法相比較,經(jīng)過神經(jīng)網(wǎng)絡(luò)優(yōu)化權(quán)重的組合預(yù)測模型在預(yù)測精度上更為準(zhǔn)確,5年的預(yù)測平均誤差為0.83%,遠(yuǎn)遠(yuǎn)低于平均組合的5.12%,該方法不但在訓(xùn)練樣本的數(shù)據(jù)擬合方面表現(xiàn)優(yōu)秀(如圖5,圖6和圖7所示),而且對測試樣本的學(xué)習(xí)效果也表現(xiàn)良好(如圖8所示),以2009年的數(shù)據(jù)為例,預(yù)測誤差為1.54%,轉(zhuǎn)換為實(shí)際的數(shù)據(jù)就是相差278億元,預(yù)測誤差非常理想,并且各模型的權(quán)值完全由歷史數(shù)據(jù)確定,不受主觀因素的干擾,因此能更客觀地反映出在組合模型中,各個模型自身的重要程度,計算結(jié)果也驗(yàn)證了基于神經(jīng)網(wǎng)絡(luò)集成的組合預(yù)測模型的有效性.將預(yù)測數(shù)據(jù)反映在圖上,如圖8所示.
4.3模型應(yīng)用
分別使用上述3個模型預(yù)測未來5年廣東省第三產(chǎn)業(yè)的生產(chǎn)總值,并且采用神經(jīng)網(wǎng)絡(luò)集成的方法將預(yù)測數(shù)據(jù)合成輸出,這里假設(shè)未來五年各指標(biāo)保持現(xiàn)有的增長速度,結(jié)果見表3所示.表32014-2018年預(yù)測結(jié)果
預(yù)測得2014年第三產(chǎn)業(yè)生產(chǎn)總值約為33 137億元,增長率為11.62%,由于廣東省2015年統(tǒng)計年鑒尚未發(fā)布,通過查詢廣東省統(tǒng)計局發(fā)布的季度統(tǒng)計數(shù)據(jù)可知道:2014年第三產(chǎn)業(yè)實(shí)際的生產(chǎn)總值為34006億元,增長率為14.55%,預(yù)測值與實(shí)際值只相差2.93%,如果再扣除當(dāng)年的消費(fèi)價格指數(shù),預(yù)測數(shù)據(jù)與實(shí)際數(shù)據(jù)是基本吻合的,可見使用神經(jīng)網(wǎng)絡(luò)組合預(yù)測模型的效果是相當(dāng)準(zhǔn)確的.
5結(jié)論
在現(xiàn)有第三產(chǎn)業(yè)發(fā)展預(yù)測研究成果的基礎(chǔ)上,針對單一預(yù)測模型的不足,構(gòu)建了基于神經(jīng)網(wǎng)絡(luò)的組合預(yù)測模型,以廣東省第三產(chǎn)業(yè)發(fā)展為例,驗(yàn)證了模型的有效性.由于組合預(yù)測方法依然處于不斷的發(fā)展和完善中,本文只是針對預(yù)測結(jié)果進(jìn)行了組合處理,如何在預(yù)測過程中,針對樣本信息和預(yù)測方法進(jìn)行有效的組合,力求做到預(yù)測的系統(tǒng)性和科學(xué)性,進(jìn)而提高預(yù)測的效果,是下一步需要研究的方向.
參考文獻(xiàn)
[1]崔二濤,肖哲.廈門市第三產(chǎn)業(yè)增加值增長預(yù)測——二次曲線指數(shù)平滑模型在第三產(chǎn)業(yè)增加值預(yù)測中的應(yīng)用[J].中國市場.2010, 582(23):54-57.
[2]呂一清,何躍.基于灰色神經(jīng)網(wǎng)絡(luò)的第三產(chǎn)業(yè)發(fā)展趨勢的預(yù)測模型[J].統(tǒng)計與決策. 2011, 382 (4) : 154 -157.
[3]徐群,于德淼,趙春閣.我國第三產(chǎn)業(yè)發(fā)展現(xiàn)狀研究及趨勢預(yù)測——基于主成分分析和逐步回歸分析[J].巢湖學(xué)院學(xué)報. 2014, 125(2):45-49.
[4]鄧偉.論ARIMA模型在廣東省第三產(chǎn)業(yè)預(yù)測中的應(yīng)用[J].現(xiàn)代商貿(mào)工業(yè). 2010,50(24):29-31.
[5]李榮麗,黃曦,葉夏,陳志強(qiáng),陳志彪.時間序列BP神經(jīng)網(wǎng)絡(luò)在福州市第三產(chǎn)業(yè)值預(yù)測中的應(yīng)用[J].江西農(nóng)業(yè)學(xué)報. 2010, 22(12):183-185.
[6]張亞峰.河南省第三產(chǎn)業(yè)發(fā)展影響因素分析及對策研究[J].江蘇商論,2011,(08):91-95.
[7]彭豐,杜洋.基于VAR模型的第三產(chǎn)業(yè)發(fā)展影響因素分析[J].現(xiàn)代商貿(mào)工業(yè),2010(17):31-33.
[8]聶曉博.邢臺市第三產(chǎn)業(yè)發(fā)展的影響因素研究[D].石家莊:河北大學(xué)經(jīng)濟(jì)學(xué)院,2013.
[9]彭森.基于粗糙集與支持向量機(jī)的工業(yè)企業(yè)經(jīng)濟(jì)景氣指數(shù)智能預(yù)測模型研究[D].武漢:華中師范大學(xué)信息管理學(xué)院,2012.
[10]張學(xué)工.關(guān)于統(tǒng)計學(xué)習(xí)理論與支持向量機(jī)[J].自動化學(xué)報. 2000, 26(1):37-39.
[11]肖健華.區(qū)域經(jīng)濟(jì)發(fā)展智能預(yù)測方法[J].經(jīng)濟(jì)數(shù)學(xué). 2005, 22(1):57-63.
[12]蔣林利.改進(jìn)的PSO算法優(yōu)化神經(jīng)網(wǎng)絡(luò)模型及其應(yīng)用研究[D].廈門:廈門大學(xué)軟件學(xué)院,2014.

