基于高職環境下微積分教學研究與實踐

徐利民

(淮南職業技術學院基礎部，　安徽淮南232001)

?

基于高職環境下微積分教學研究與實踐

徐利民

(淮南職業技術學院基礎部，安徽淮南232001)

[摘要]在高等職業教育進入普及化時代，借鑒工業產品質量標準理念提高教育質量的思想已被普遍所重視，微積分教學系統設計需要統籌考慮學生的數學基礎與教學目標的要求,為實現夠用的教學原則，通過對微積分教學的通俗性、直觀性和教學內容的實用性的研究，探討了教學實踐中提高教學效率和實現雙基教學的策略問題。

[關鍵詞]高職教育；微積分；雙基教學；教學策略

一、引言

高等職業教育已進入普及化的時代，隨著招生制度的改革，高等職業教育教學的主要對象是那些“愿意接受高等職業教育的普通高中和中職畢業生”。針對高等職業教育新的教學形勢，教育部等六部門在《現代職業教育體系建設規劃(2014-2020年)》(教發[2014]6號)文件中指出:職業院校按照真實環境真學真做，掌握真本領的要求開展教學活動。安徽省教委在(皖教職成[2015]10號)文件中指出：高等職業教育要“科學把握公共基礎課的功能定位，促進公共基礎課與專業課程之間的融通和有效配合”，“推進課程內容的銜接，統籌安排中高職銜接專業的公共基礎課”等。

《微積分》教學內容研究的對象是初等函數和少量的分段函數，教學中需要適合的基本初等函數的知識和函數演算能力。而數學演算能力也一直是學院學生的弱項，并且在一個較短的時間內，通過一些練習也難以彌補，這也影響到數學教學的進度和學生課后獨立完成作業的能力，這樣期望通過課后練習來深化理解概念和定理等教學內容的教學方式不能獲得實際滿意的教學效果，從而影響到學生的應用能力和許多學生學習的積極性[1]。

在新的教學形勢下，數學教學怎樣適應高等職業教育培養技能型應用人才的要求，克服學生數學基礎與教學時數緊缺的條件制約，搞好數學教學系統設計，提高教學效率，在較短的教學時間內，使學生能夠理解《微積分》的基本原理，達到夠用的教學原則，增加學生數學應用能力，將是一個迫切需要研究的問題。

二、高職環境下微積分教學的質量要求

質量沒有最好的，只有更適應的。高等職業教育教學必須克服“應用型人才的培養與傳統的教學理念、課程知識體系等之間的矛盾”[2]，樹立現代高等教育管理理念和質量意識。高等教育引入工業產品質量管理理念與經驗，提高教育質量，已被普遍所接受。由ISO9000質量管理標準質量管理原則中指出:以顧客為關注焦點，組織應當理解顧客當前和未來的需求，滿足顧客要求并爭取超越顧客期望。因而數學教學系統的組織依賴于社會和專業建設對當前和未來的需求，數學的教學內容應當滿足顧客要求并努力超越顧客的期望。學生是教學管理的對象，也是教學服務的對象，因此在課程建設中，《微積分》教學內容設計需要統籌考慮學生的數學基礎、專業課程以及實際服務社會的需要，求得適應性。知識是課程建設的產品，知識應該是學生能夠聽得懂和學得會的，產品應該是社會與企業所需要的.在高等職業教育中，通俗易懂、簡明直觀、實際真實有用是數學課程內容建設的要求。

三、高職環境下微積分雙基教學的策略

《微積分》是以極限理論為基礎，微分與積分兩大概念理論為支撐的理論體系，微分(導數)與積分兩大基本概念是建立《微積分》課程與專業課程之間聯系的基礎，也是《微積分》教學內容應用的基礎。因此在高等職業教育中，首先要著重于基礎知識的教學，實現夠用的教學原則。而要做好基礎知識的教學，需要做好基礎知識的通俗性和直觀性教學的研究，探索適應的教學內容和教學方法，克服條件的制約，以提高學生對教學內容的理解能力，達到或超過社會對高等職業教育要求，增加教學的有效性。要提高學生的數學應用能力，具體需要建立微分(導數)和積分與其他專業課程中物理量之間的聯系，開展相應的教學內容研究，提高學生數學應用的基本技能，促進對數學教學內容的理解與數學情感，提高教學效果。

(一) 中高職知識銜接問題

在高等職業教育中，微積分教學內容是以描述性極限定義為基礎，在嚴密性方面降低了要求，對基本初等函數的連續性也不再重構，而就其函數的極限、連續性和函數的導數(微分)的研究方法是通過基本初等函數的極限、連續性和導數來實現初等函數的極限、連續性和導數的計算和研究，即四則運算和復合運算的法則。在新的教學形勢下，面對教學時數資源緊缺和學生的數學基礎問題，教學中應充分利用學生在中學階段對基本初等函數的圖像和連續性的認識開展教學，利用基本初等函數的圖像實現基本初等函數的極限判斷，可以增加教學的直觀性，有利于教學知識的銜接問題，提高教學效率。

(二) 教學內容陳述的通俗化

數學嚴謹性的一個方面在于以嚴密的數量關系來表達數量和數量與數量之間的關系，幫助學生理解這些數量和數量之間的關系是數學教學的主要任務。在高等職業《微積分》教學中，除極限概念外，其他數量以及數量之間關系的數值表達式也同樣需要一種聽得懂或看得懂的陳述方式，使其學生能夠進一步理解較為深一層的數值或物理含義，以便能夠達到提高學生應用能力的要求。

微積分教學內容通俗化，自然離不開教學語言的通俗化，除極限概念的通俗語言表述外，也需要把數學嚴密的數值表述轉換為通俗的語言表述，來提高學生的理解了能力。為學生答疑解惑，需要努力精煉語言和積累經驗。

(三) 直觀化教學

1.用圖像表示函數的性質

《微積分》教學內容研究的是函數，函數的許多性質可以通過函數的圖像來表示，或者說通過研究函數的圖像可以獲得函數的一些性質。研究使用函數的圖像來直觀的表達函數數值特征和數量關系，或使用函數圖像來分析函數的數值特征，分析定理和定義，避免使用復雜的數值邏輯分析，以便提高學生的理解能力，提高教學效率。

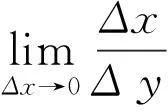
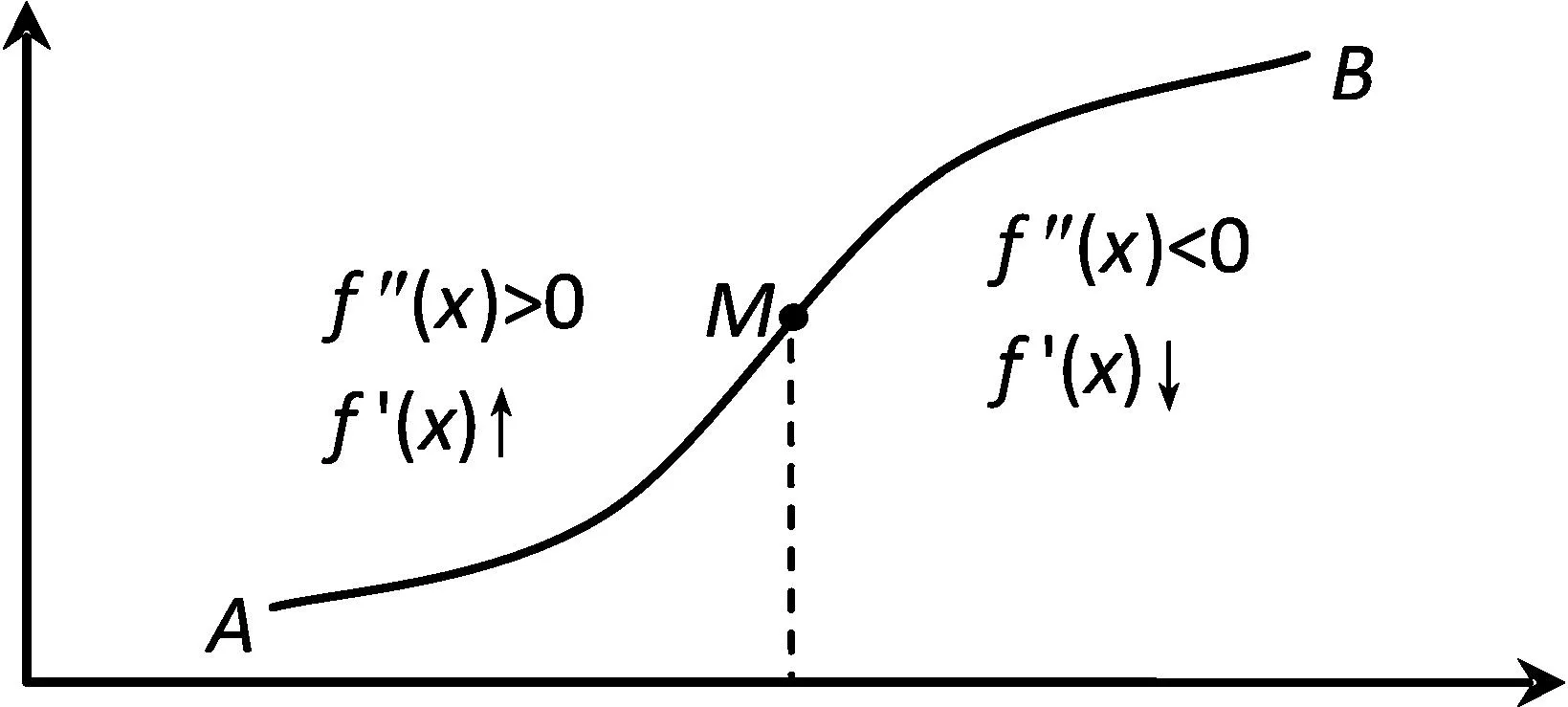
圖1　戈珀斯曲線

2.用動畫描述變量的變化趨勢

《微積分》是以運動的方法來研究函數的，即當自變量在某個變化(x→x0，或x→∞等)狀態時，函數值具有某種變化趨勢，利用多媒體教學課件和視頻課件的優勢特點，提高視覺效果，開展數學直觀教學的研究，制作更為合適的圖像或動畫，直觀地表達數量與數量的關系，演示自變量和函數值的變化過程等，來提高教學效果，增加學生的理解力，比傳統的板書教學具有明顯的優點。

(四) 教學內容的簡化

在微積分教學內容中除極限、連續性的判斷，以及導數運算都具有四則運算和復合運算法則的共性外，認真分析研究教學內容，利用相似教學內容之間存在的共性，總結和整合教學內容，可以提高教學效率，同時也能提高學生的理解與記憶。如f′(x)的符號反映了函數f(x)的單調性，自然f″(x)的符號反應了導函數f′(x)的單調性，且同時f″(x)的符號也反映了函數曲線的凸凹性。因此極值點是單調區間的分界點，而導函數單調區間的分界點對應函數曲線上的點是函數曲線的拐點。

四、應用數學模型教學探索

把數學模型引入《微積分》教學，建立數學與實際應用之間的聯系，提高學生的數學應用能力和認識，在高等職業教育中需要認真把握和研究，遵循夠用的教學原則，綜合考慮實際教學情況和實際真實應用，搞好教學設計。

在《微積分》教學內容與實際應用之間的聯系中，導數通常表示某個量的流量(某個量在單位時間內流動的量)或者某個量的變化速度，如在電子技術中可以表示電荷的流量(電流)，在煤礦通風系統中導數可以表示瓦斯的流量和風的流量，還有或物質流量和資金流量等。而一個量的總量表示為流量的積分。

當系統的穩定(或平衡)條件被破壞時, 系統的狀態將發生轉移, 將從一種穩定狀態趨向于另一個穩定狀態， 這是一種較為普遍的自然變化規律。

設t時刻流體流入容器的輸入流量 (輸入速度)為vin=vin(t), 流出容器的輸出流量為vout=vout(t)。又設從0時刻至t時刻容器RQ內流體的總量為Q′(t), 所以容器內流體總量變化的速度 。

數學模型為:Q′(t)=vin(t)-vout(t),即容器內流體總量增加的速度等于流體流入的速度減去流體流出的速度。

系統的平衡條件為：vin(t)-vout(t) 。

在煤炭專業數學教學中，利用數學模型理解煤礦通風系統中區域瓦斯排放過程，以及煤礦局部區域瓦斯濃度的變化規律，開展煤礦安全生產教育和數學應用教學.

設vin(t)表示輸入瓦斯流量，vout(t)表示輸出瓦斯流量，Q(t)表示系統容器(煤礦某局部區域)中累積的瓦斯總量(m3)。當輸入瓦斯流量vin(t)大于輸出瓦斯流量vout(t)時，Q′(t)>0 ，區域瓦斯累積總量Q(t)(m3)上升，局部區域瓦斯濃度上升。當輸入瓦斯流量vin(t)小于輸出瓦斯流量vout(t)時，Q′(t)<0，區域瓦斯累積總量Q(t)(m3)下降，局部區域瓦斯濃度下降。

在與電子技術相關專業數學教學中，設vin(t)表示輸入電流，vout(t)表示輸出電流，Q(t)表示系統容器中累積的電量。電容兩端電壓差的(或Q(t))穩定條件是輸入電流vin(t)等于輸出電流vout(t)。 根據不同的專業，強調不同方面的應用。對不同的專業舉一反三地突出某一方面流量的表述和應用，增強學生的理解和數學的應用能力，滿足數學應用教學的要求，也有利于提高高等職業教育整體教學的效率。

五、結語

知識是課程設計的產品，知識應該是學生聽得懂的與學得會的，產品應該是社會企業所需要的。在高等職業教育數學教學系統設計中，應該統籌考慮學生的數學基礎與社會企業的需求，做好中等教育與高等職業教學數學知識的銜接教學工作。為實現高等職業教育應用型人才的培養目標，滿足社會企業對應用型人才的要求，需要克服學生的數學基礎和教學時數緊缺等條件的制約，積極開展教學內容的適應性、通俗性和直觀教學的研究，并在教學中不斷積累和總結經驗，不斷提高教師的教育技術水平，才能適應新形勢下高等職業教育發展的要求，實現夠用教學原則。

參考文獻:

[1]徐利民,梅燦華,白灝,等.基于高職環境下微積分教學內容的研究[J].淮南職業技術學院學報,2015(1):80-83.

[2]劉振天.沒有最好只有更適合[N].中國教育報,2012-05-28(08).

[3]R.柯朗.什么是數學[M].北京：科學出版社，1985.

[4]張景中，馮勇.第三代的微積分[J].自然雜志,2010,32(2):67-71.

[5]高雪芬.一元微積分概念教學的設計研究[D].上海：華東師范大學,2013.

[6]孫靜懿.高數教學中數學建模思想融入實踐研究[J].內蒙古師范大學學報(教育科學版),2014(10):61-63.[7]屠大華.現代教育理論[M].武漢：華中科技大學出版社，2002.

[收稿日期]2016-02-24

[基金項目]安徽省高等教育振興計劃重大教學改革研究項目：發揮企業辦學主體作用，煤炭類技術技能人才系統培養研究與實踐(項目編號：2014ZDJY156 );安徽省高等學校質量工程研究項目：精品資源共享課程《高等數學》(項目編號：2013gxk118)

[作者簡介]徐利民(1961-),男,江蘇宜興人,副教授,從事教學與研究工作,電話：0554-6656025。

[中圖分類號]O172.4;G712.4

[文獻標識碼]A

[文章編號]1671-4733(2016)04-0074-04

DOI:10.3969/j.issn.1671-4733.2016.04.020