求概率的常用方法
文/王宗俊
?
求概率的常用方法
文/王宗俊
責任編輯:王二喜

概率是中考的必考內容.下面以2015年中考題為例,歸納求概率的常用方法,供你學習時參考.
一、用公式P(A)=求概率
例1(2015年臺州卷)有四張質地、大小、反面完全相同的不透明紙片,正面分別寫著數字1、2、3、4,現把它們的正面朝下,隨機擺放在桌面上,從中任意抽出一張,則抽出的數字是奇數的概率是________.
解析:四張分別標有數字1、2、3、4的紙片中,其中奇數卡片有兩張,所以從四張紙片中任意抽出一張,抽出的數字是奇數的概率為
溫馨小提示:如果一個事件有n種可能,而且這些事件發(fā)生的可能性相同,其中事件A出現m種結果,那么事件A發(fā)生的概率用公式求概率是最常用的一種方法.
例2(2015年呼和浩特卷)如圖1,四邊形 ABCD是菱形,E、F、G、H分別是各邊的中點,隨機向菱形ABCD內擲一粒米,則米粒落到陰影區(qū)域內的概率是________.
解:如圖1,連接DB,AC.

圖1

溫馨小提示:求幾何型概率問題,需要熟悉圖形的有關性質,運用整體思想、化歸思想等求面積.這類題型成為近年中考常見題型.一般用幾何圖形的面積比求概率.
三、用頻率估計概率
例3(2015年揚州卷)色盲是伴X染色體隱性先天遺傳病,患者中男性遠多于女性,從男性體檢信息庫中隨機抽取體檢表,統(tǒng)計結果如下表:

抽取的體檢表數n色盲患者的頻數m色盲患者的頻率m/n 50 3 0.060 100 7 0.070 200 13 0.065 400 29 0.073 500 37 0.074 800 55 0.069 1000 69 0.069 1200 85 0.071 1500 105 0.070 2000 138 0.069
根據上表,估計在男性中,男性患色盲的概率為________(結果精確到0.01).
解析:觀察表格,可以發(fā)現色盲患者的頻率在0.07左右波動,填0.07.
溫馨小提示:大量重復試驗下,某事件發(fā)生的頻率會穩(wěn)定在某個常數的附近,這個常數就是該事件概率的估計值.
四、用列表法求概率
例4(2015年貴陽卷)在“陽光體育”活動時間,小英、小麗、小敏、小潔四位同學進行一次羽毛球單打比賽,要從中選出兩位同學打第一場比賽.
(1)若已確定小英打第一場,再從其余三位同學中隨機選取一位,求恰好選中小麗同學的概率;
(2)用畫樹狀圖或列表的方法,求恰好選中小敏、小潔兩位同學進行比賽的概率.
解析:(1)從三位同學中選中小麗同學只有1種情況,所有可能的情況共有3種,∴恰好選中小麗同學的概率是.
(2)列表:

小英小麗(小麗,小英)小敏(小敏,小英)(小敏,小麗)小潔(小潔,小英)(小潔,小麗)(小潔,小敏)小英小麗小敏小潔(小英,小麗)(小英,小敏)(小英,小潔)(小麗,小敏)(小麗,小潔)(小敏,小潔)
從表中可以看出,小敏同小潔比賽的情況有2種,而所有可能的情況有12種,選中小敏、小潔比賽的概率是
溫馨小提示:列表的目的在于不重不漏地列舉出所有可能的結果,即求出n,從中選出符合事件A的數目m,求出概率.列舉法求概率的關鍵在于列舉出所有可能的結果.當有兩個元素時,可以用列表法列舉,也可用樹形圖列舉.
五、畫樹形圖求概率
例5(2015年常州卷)甲、乙、丙三位學生進入了“校園朗誦比賽”冠軍、亞軍和季軍的決賽,他們將通過抽簽來決定比賽的出場順序.
(1)求甲第一個出場的概率;
(2)求甲比乙先出場的概率.
解析:(1)甲、乙、丙三位學生都有可能第一個出場,共有三種可能,所以甲第一個出場的概率為
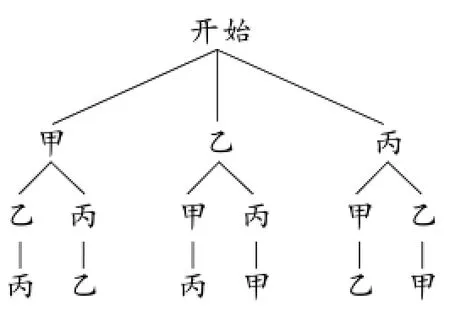
(2)樹形圖如下:共有6種情況,其中甲比乙先出場的有3種,∴P(甲比乙先出場)=
溫馨小提示:樹形圖法適用于事件涉及兩個或更多的元素,能不重不漏地列出所有可能的結果.當事件在三步或者三步以上時,用樹形圖求解比較方便.

