基于貝葉斯正則化BP神經網絡的鋁平板超高速撞擊損傷模式識別

劉　源， 龐寶君

(哈爾濱工業大學 航天學院，哈爾濱　150080)

基于貝葉斯正則化BP神經網絡的鋁平板超高速撞擊損傷模式識別

劉源， 龐寶君

(哈爾濱工業大學 航天學院，哈爾濱150080)

損傷模式識別是空間碎片撞擊航天器在軌感知技術中的一個重要功能模塊，是目前研究的重點和難點。采用超高速撞擊聲發射技術，以鋁合金平板為研究對象，通過大量超高速撞擊實驗獲取實驗信號，結合虛擬波陣面的精確源定位技術、時頻分析技術及小波分解技術。從超高速撞擊聲發射信號中提取并優選與損傷模式直接相關的時頻參數，建立了基于貝葉斯正則化BP神經網絡的損傷模式識別方法，識別了鋁合金板面受撞擊形成的成坑/穿孔兩種主要損傷模式。

空間碎片；超高速撞擊；聲發射；神經網絡；損傷模式識別

迄今為止人類進行了近5 000次航天發射活動，為空間科學的發展做出的重大貢獻，同時產生的大量空間碎片遺留在軌道空間中，尤其對長期在軌運行的大型航天器的安全問題產生很大威脅[1]。其中毫米級別的空間碎片威脅最大，因其體積小、難以通過觀測手段獲知其準確運行軌道并進行規避。為保障大型航天器在軌安全性，需要實時感知其受空間碎片撞擊情況。這種能夠實現感知空間碎片超高速撞擊情況的系統被稱為“在軌感知系統”。其中基于聲發射的感知系統具有較好的可實現性，且具有較高的定位能力，國外已研究和開發了相關感知系統，如LAD-C(Large Area Debris Collector)、DIDS(Distributed Impact Detector System)、MDD(Micro-meteoroid/space Detris Detector)等[2-4]；國內也針對該技術進行研究，并取得了大量的研究成果[5-8]。目前，在軌感知系統主要包括撞擊感知和源定位模塊，為提高在軌感知系統的智能水平、深化感知能力，還需要增加損傷模式識別模塊，用于識別航天器受損情況及程度。

為開發一種可行的超高速撞擊損傷模式識別技術，需通過大量實驗獲取聲發射信號，采用多種時頻分析手段獲得參數，優選和提取與損傷模式相關的作為損傷參數，建立貝葉斯正則化人工BP(Back Propagation)神經網絡模型，通過對網絡進行優選確定的網絡結構，并結合實驗信號中的聲發射信號特征建立神經網絡。

1損傷模式識別模型及貝葉斯正則化網絡

1.1損傷模式識別模型

空間碎片撞擊在航天器表面產生撞擊聲發射信號，以Lamb波的形式傳播，由于撞擊時發生彈塑性形變及相變等過程，會產生頻率豐富、模態多樣的Lamb波。根據工程需要，航天器在軌運行中需要主要考慮是否被擊穿，是否發生氣體泄漏，因此將損傷模式分為成坑和穿孔兩類。

1) 成坑：靶板被撞擊后撞擊位置不透光，主要包括靶板背面未彎曲、背面較小程度彎曲、背面發生層裂、背面有較少材料剝落等幾種損傷模式；

2) 穿孔：靶板被撞擊后撞擊位置透光，主要包括靶板背面有較大剝落、撞擊坑與剝落相遇造成的孔洞等幾種損傷模式，并且將彈丸在臨界速度時的臨界穿孔模式也歸入該類，以提高航天器的安全性。

為實現超高速撞擊損傷模式識別，將基礎建立在超高速撞擊實驗上，選取合適特征建立特征庫，并輸入至人工神經網絡進行訓練。

1.2貝葉斯正則化方法

BP神經網絡指的是基于BP算法的多層向前神經網絡，通過誤差控制信息的傳遞，當輸出結果誤差大于期望值時，誤差以一種形式通過隱含層向輸入層返回，進而影響網絡內部的全部單元，獲得各層單元的誤差信號，作為修正網絡權值的依據。這種網絡模型的特點是由輸入節點層、隱含節點層、輸出節點層級層間連接節點構成，神經元之間的連接計算僅在層內進行，且每層之間不通過反饋。

選取超高速撞擊損傷模式識別所用參數，建立多種類型和結構的BP神經網絡，對成坑/穿孔狀態的損傷模式進行識別，當選擇包含4個隱含層，每層分別有10個節點的貝葉斯正則化BP神經網絡時，網絡的訓練速率最快，識別率最高，且結構也最為精簡。

正則化理論可以很好的提高網絡的泛化能力，貝葉斯正則化算法是通過修正神經網絡的性能函數來提高優化能力的[10-12]，是在一種變形的牛頓法(Leven-berg-Marquardt,LM)算法基礎上修正的網絡算法。該算法是在LM算法的性能函數誤差反饋的基礎上，加入了權值的反饋，因此其網絡的訓練函數可以寫成:

F=αEω+βED

(1)

式中：Eω為全部網絡權值平方和;ED為每層網絡輸出值與真實值之間的誤差值;α和β分別為性能函數的正則化系數；表達式見式(2)。系數的值代表網絡訓練的側重，當α<β時，隨著訓練次數的增加，訓練樣本的誤差逐漸變小；當α>β時，隨著訓練次數的增加，權值逐漸變小，平滑網絡輸出。

(2)

式中：γ為有效參數的數量，表征能夠降低訓練誤差的神經網絡的連接權值數量;n為全部的訓練樣本數量。

γ=n-2α·tr(H-1)

(3)

式中：H為性能函數的海森矩陣。

H=α2Eω+β2ED

(4)

2超高速撞擊實驗

利用哈爾濱工業大學高速撞擊研究中心的二級輕氣炮進行實驗，彈丸采用Φ3.2 mm的2017鋁合金球彈丸。選取典型衛星結構的鋁合金平板作為研究對象，靶板規格為450 mm×450 mm×5 mm。采集系統的采集頻率為25 MHz，單次采集總時長1.25 ms，充分的保證充分獲取原始信號和噪聲信號，其中包含原始信號及兩次反射后的信號，通過計算導波的頻散曲線，結合實驗可知靶板面上聲發射信號傳播的最快速度約5 300 m/s。每次實驗在平面上側安裝6枚聲發射傳感器，傳感器的布置見圖1(a)，標號4～9，以正方形中心為原點，各個傳感器距離中心100～250 mm，記錄每個安裝位置獲取的聲發射信號。傳感器的真實布置情況見圖1(b)。超高速撞擊實驗進行42次，實驗結果中的成坑和穿孔模式見圖2，共獲得252個鋁合金平板超高速撞擊聲發射信號。

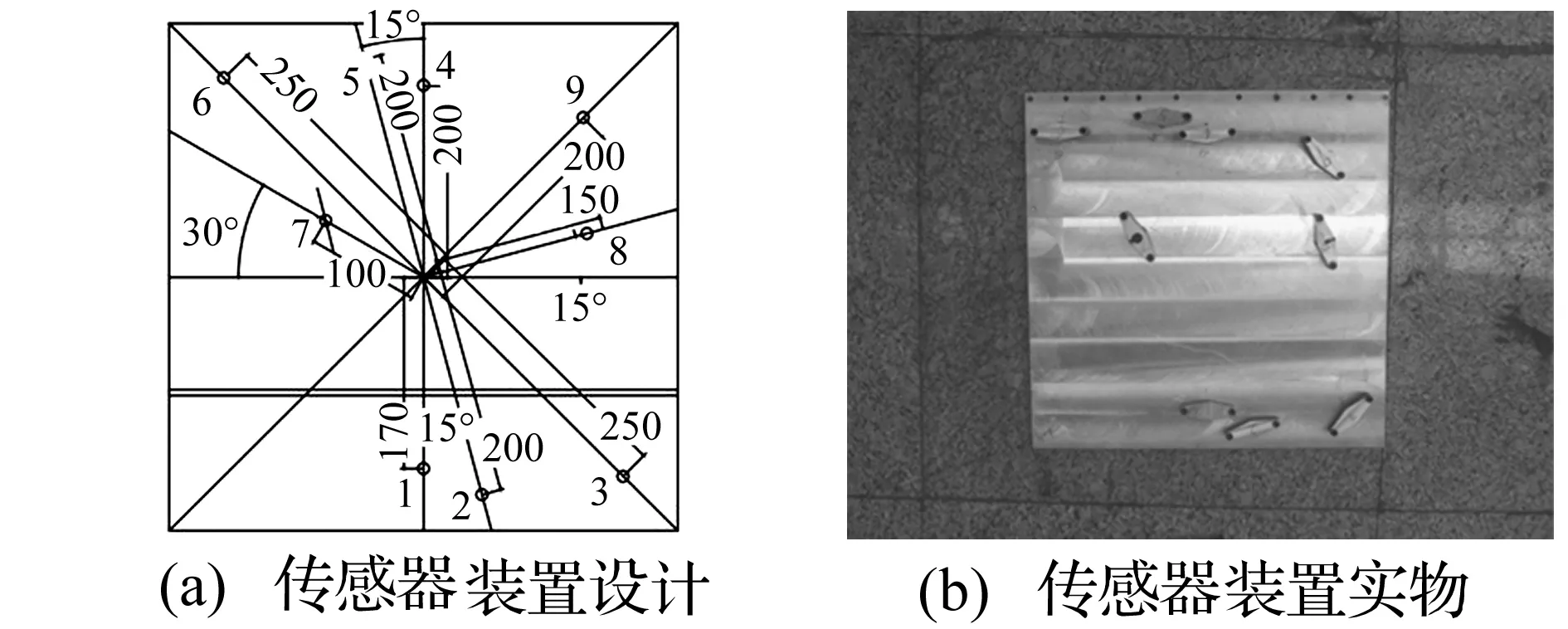
圖1　傳感器裝置方法Fig.1 Sensor conformation

根據“1.1”將損傷模式分為成坑和穿孔兩類，為能夠對成坑和穿孔的進行獨立識別，實驗中的成坑實驗和穿孔實驗數量保持大致相同，實驗中成坑22次，穿孔20次(包括一次臨界穿孔)，由于每個實驗靶上均裝置6枚傳感器，因此獲得成坑實驗信號132個，穿孔實驗信號120個。

圖2　靶板背面超高速撞擊損傷情況Fig.2 Hypervelocity impact damage in the back of target

3損傷特征的選取

3.1傳播距離

Lamb波信號中各個分量在傳播過程中的衰減程度是不同的，因此推測傳播距離應為制約算法識別能力的重要參數。采用了一種基于虛擬波陣面的精確源定位方法計算撞擊源位置，根據該通道傳感器安裝位置計算得信號的傳播距離。

在實驗中選取1、6、9三個通道作為定位角陣，對超高速撞擊聲發射信號進行定位。經驗證，考慮傳感器的位置誤差，平均定位誤差約為5 mm。根據板面上板波衰減規律，毫米級別的距離誤差對波動中各個分量的影響可以忽略。

3.2時域特征

根據靶板尺寸和波速可知，整體信號實際上是由第1次完整的聲發射信號與2次反射信號構成的，首先對信號進行預處理，消除大部分由反射造成的干擾。由圖3(a)可知為原始信號，反射信號與一個負向極大的低頻脈沖幾乎同時到達，該脈沖的幅值大于原始信號中的最大幅值，且頻譜遠低于20 kHz，低于超聲波段。根據彈性波反射的波形耦合原理可知，其與入射波屬于兩種不同模態，因此認為該負向脈沖與原超高速撞擊聲發射信號無關。設計一個通帶為20 kHz，阻帶50 kHz的高通濾波器降低其影響，這種濾波方式可以去掉低頻信號的影響。

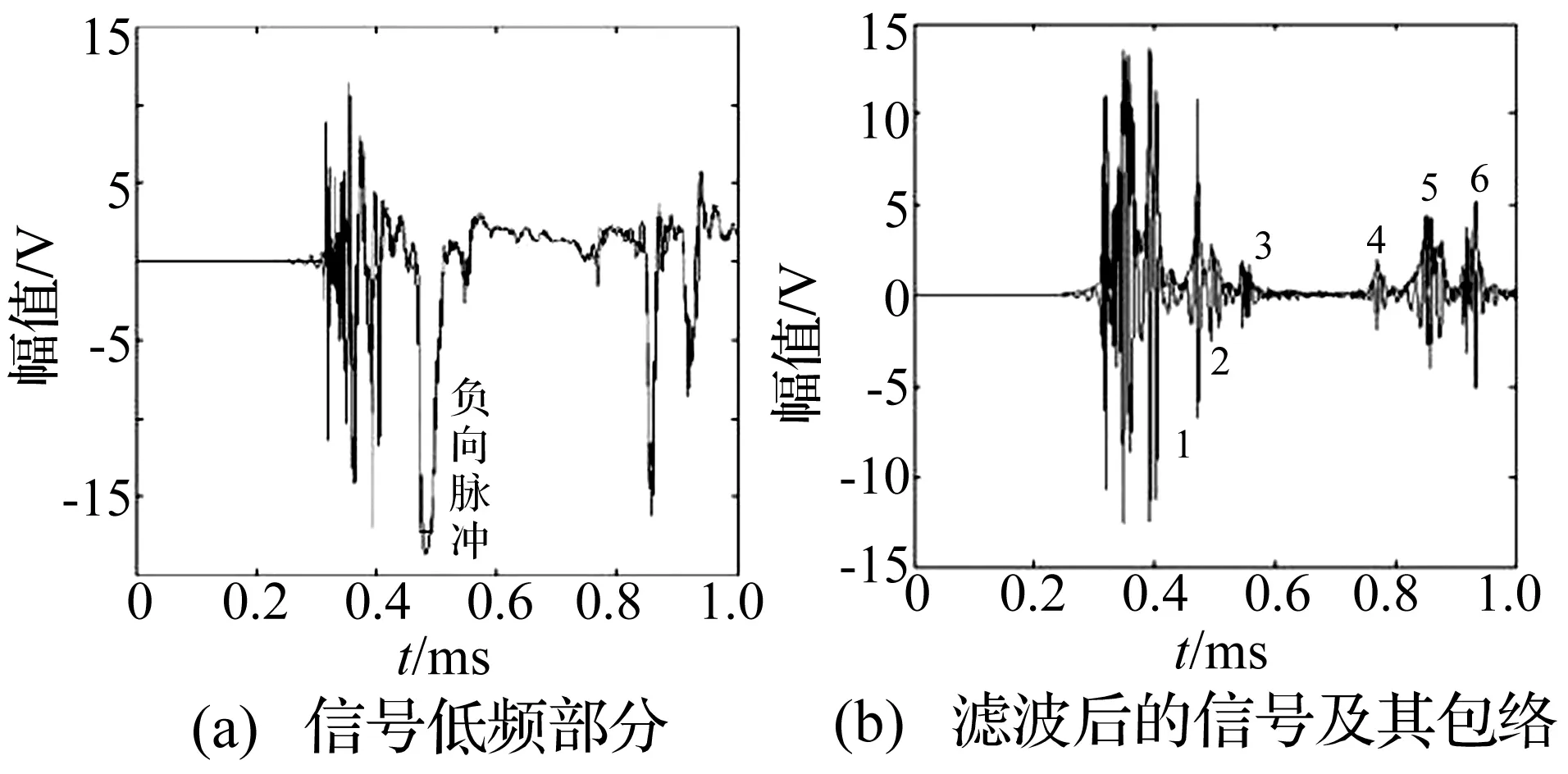
圖3　高速撞擊聲發射信號的波形處理Fig.3 Waveform processing of hypervelocity impact acoustic emission signal

圖3(b)為濾波后的波形，可以清楚地看出，濾波后的部分主要包含6個波包，分別對應了原始信號和反射信號中的各個模態成分。

信號的持續時間記錄信號第1個波包的持續時間，如圖4(a)所示為信號濾波后成分的包絡。采用自動閾值法獲取信號的持續時間，門檻選取整個包絡的均值。當連續有5個采樣點超過了均值水平時記為信號開始，當第一次連續5個采樣點低于門檻時記為原始信號截止。對于鋁合金平板來說，撞擊速度與損傷情況呈單調變化關系，計算252個實驗數據的信號持續時間，如圖 4(b)所示。

信號的上升時間定義為信號從到達時刻到峰值最大時刻的時間，見圖 5(a)。計算252組樣本的上升時間見圖 5(b)，可知上升時間與撞擊速度之間的關系比較離散，以150～200 μs之間為中心分布，這是由于信號傳播距離受靶板尺寸限制，因此信號第一次到達傳感器的時間始終處于這個范圍。

圖4　超高速撞擊聲發射信號持續時間與撞擊速度關系Fig.4 Relation between time of hypervelocity impact signal duration and impact velocity

圖5　信號的上升時間與撞擊速度的關系Fig.5 Relation between rise-time of hypervelocity impact signal and impact velocity

3.3頻域特征

由實驗可知超高速撞擊聲發射信號在頻譜中主要分布于0～600 kHz和600～1 200 kHz兩個頻段內，其中高頻分量較少，見圖6(a)，因此只分析低頻部分。研究表明，聲發射信號不同模態的中心頻率與撞擊速度無關，但截止頻率通常與初始撞擊速度有一定關聯，因此計算聲發射信號低頻部分起始和截止頻率，這里采用自動閾值法獲取。

自動閾值法的流程為：

1) 對信號進行傅里葉變換；

2) 抽取變換序列中對應2～3 MHz部分；

3) 計算抽取部分的平均值m；

4) 以5×m作為門檻閾值；

5) 計算頻譜中第1次高于門檻閾值的頻譜為起始頻率，之后第1次低于門檻閾值的頻率為截止頻率。

由于濾波的關系，起始頻率與撞擊速度為一個無關的量，因此僅考慮截止頻率，圖6(b)為截止頻率與彈丸發射速度的關系圖。

圖6(b)趨勢表明，截止頻率與撞擊速度之間近似呈單調下降關系，撞擊速度越高截止頻率越低，隨著撞擊速度的增加，損傷情況加深，低頻部分的頻譜越來越集中，在3 km/s以后達到穩定，這個速度與靶板的極限速度相近，說明當靶板發生穿孔后，低頻部分的截止頻率可保持在一個穩定范圍內。

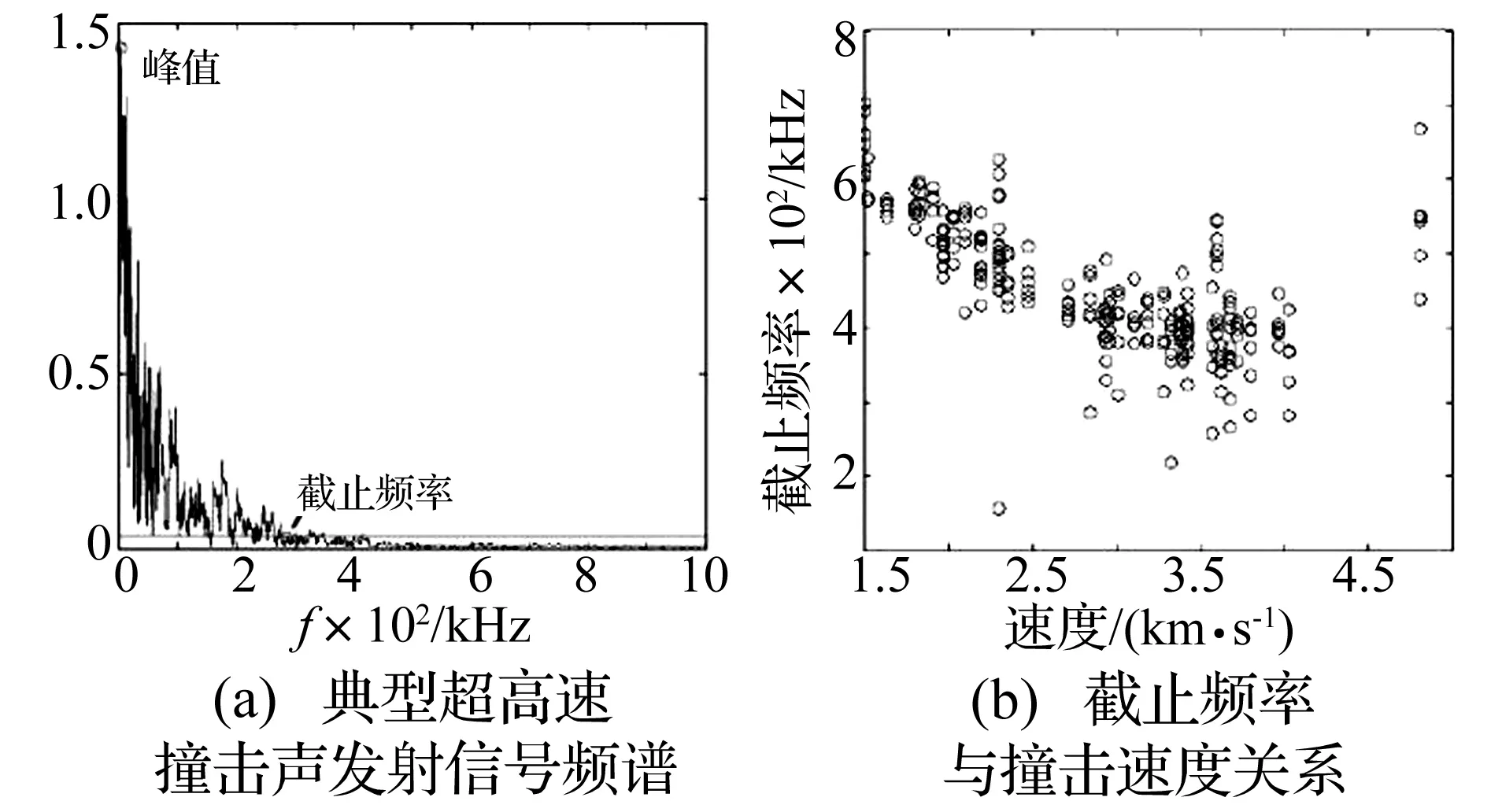
圖6　超高速撞擊聲發射信號截止頻率及與撞擊速度的關系Fig.6 Relation between cut-off frequency and impact velocity

3.4小波能量分數

采用小波分解將信號分解成不同頻率的成分，實驗中采樣率遠高于信號的截止頻率，先對信號進行重采樣，使信號的采樣率降至2 MHz，通過對比Ciofct、Haar、Symmlet、Daubechies、Biorthogonal、ReverseBio、Demyer等小波基對超高速撞擊聲發射信號進行的分析，發現其中Daubechies4小波4階以上分解，可以將超高速撞擊聲發射信號的不同模態進行有效的分離。采用Daubechies4小波5層分解(見圖7)，分離信號中不同頻譜的分量。

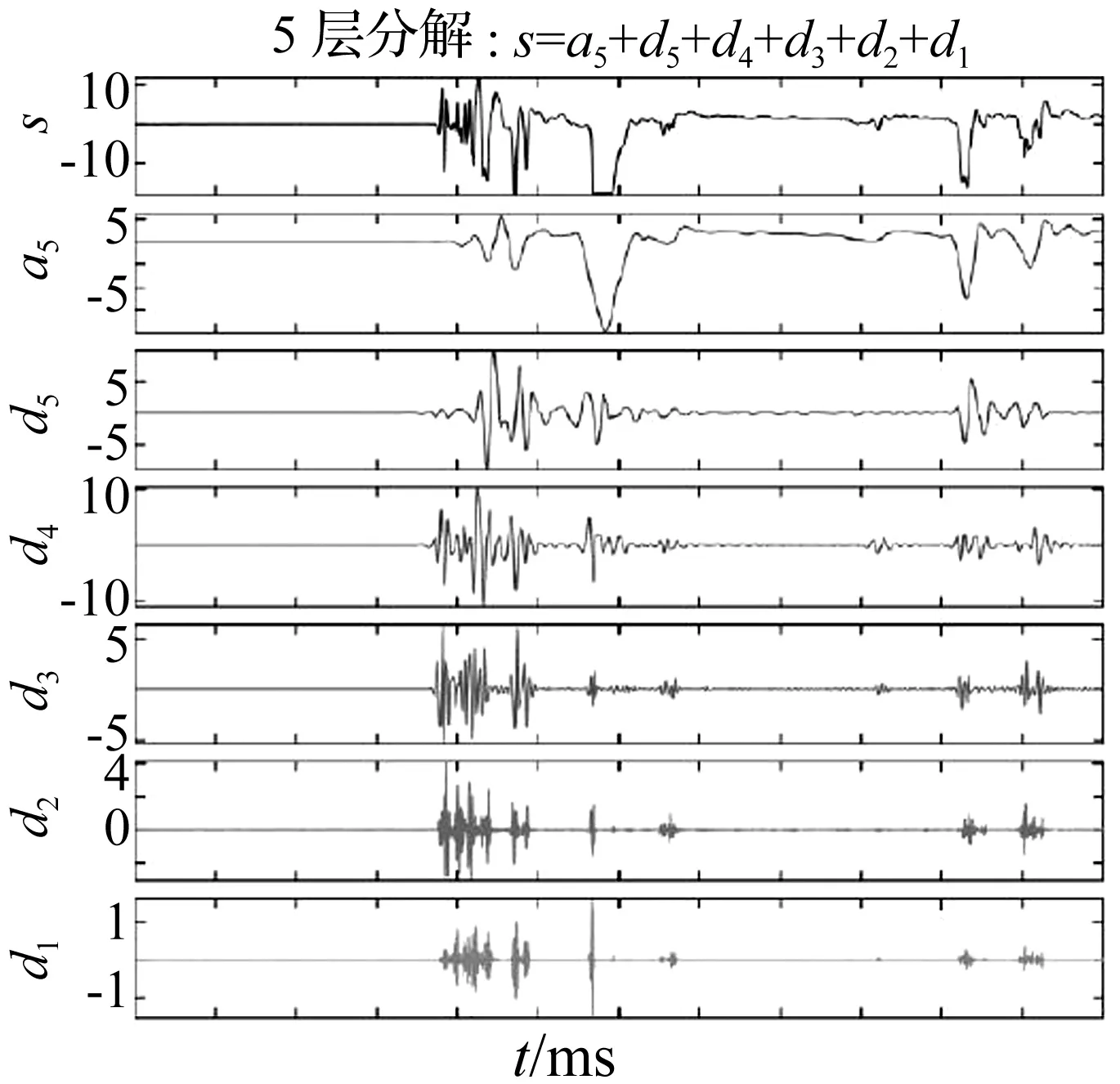
圖7　超高速撞擊聲發射信號Daubechies4小波5層分解圖Fig.7 Daubechies4 wavelet decomposition figure of hypervelocity impact acoustic emission signal

由于單次實驗的安裝有差異，各個傳感器裝置的預應力不同，且信號各個成分的能量隨著傳播距離的增加而不斷變小，因此直接計算信號的能量是不合理的，提出一種小波能量分數，其計算過程為：

1) 選用一種表征小波分解后分量在假設原始的信號為F，首先對信號進行調平；

2) 對信號進行重采樣至2 MHz，將這個調整過的信號記為F′；

3) 經過Daubechies4小波施行5層分解，分解后的成分為F=(f1,f2,f3…，fn)等n個子分量，且總的信號和這些分量均滿足關系：

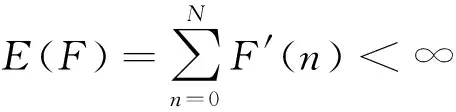
(5)

4) 計算各個子分量的能量值

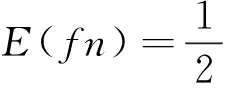
(6)

5) 計算各個小波子分量的能量分數

(7)

以小波能量分數作為損傷模式識別特征參數，可以直觀地表達隨著傳播距離和損傷模式的變化，信號中特征值的變化規律。對信號進行5層分解后得到6個特征參數。圖8代表了特征參數隨初始撞擊速度的變化關系，從圖8可知在(0～62.5 kHz)的頻率范圍內，能量分數與載荷無關；頻率范圍在(62.5～125 kHz)、(125～250 kHz)、(250～500 kHz)以內的關系圖表示，初始速度小于3 km/s時，能量比近似單調下降，在3 km/s附近停止；當頻譜在(500～1 000 kHz)時，能量比是隨著彈丸的發射速度單調上升的；當頻譜在(1 000～2 000 kHz)時，能量比以一個較小的斜率變化的。這說明能量分數與損傷模式之間是相關的。因此損傷參數選(62.5～2 000 kHz)范圍內的5個分量。

圖8　小波能量分數與撞擊速度的關系Fig.8 Relation between wavelet power ratio and impact velocity

4損傷模式識別結果分析

以傳播距離、時域特征、頻域特征、小波能量分數作為特征向量輸入，對算法的可靠性進行驗證。選取全部的252次訓練樣本作為訓練數據，建立貝葉斯正則化BP神經網絡模型，以0表征成坑損傷模式，以1表征穿孔模式，網絡模型見圖9。

圖9　神經網絡結構Fig.9 Neural network structure

對損傷模式識別所用參數進行優選，選擇最合理的搭配(見表1)。

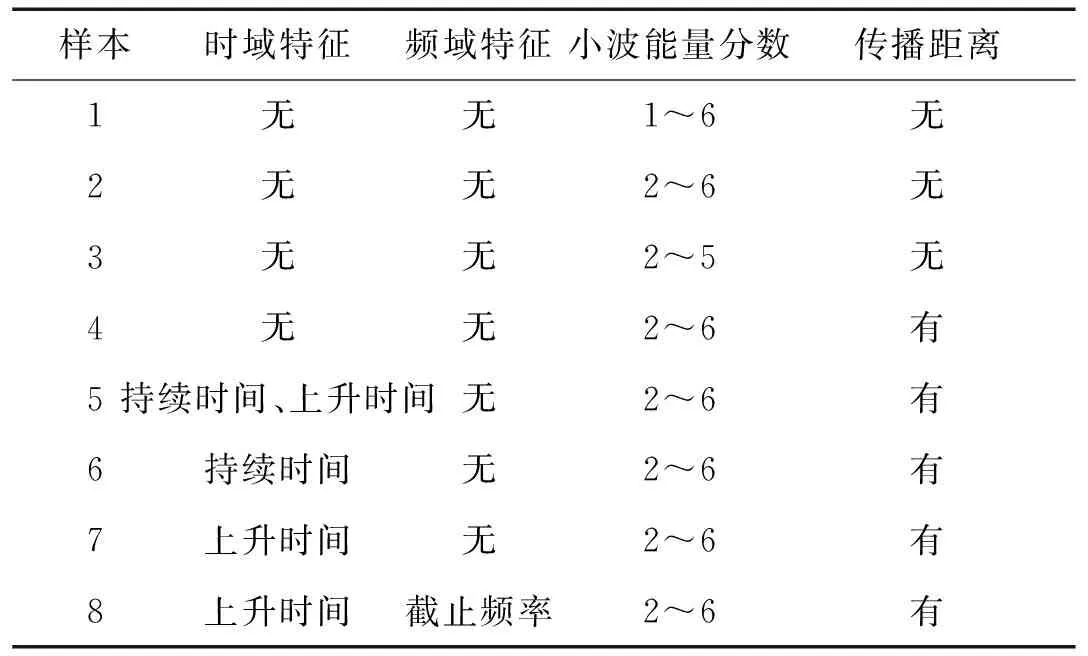
表1　輸入參數列表

為評估算法的識別能力及識別算法帶來的風險，深入分析識別算法對成坑、穿孔兩種模式的區分能力，提出4個識別指標：穿孔識別率、成坑識別率、錯分率和風險，這些網絡計算值與期望值件允許的最大誤差K取0.2。其中穿孔識別率代表了全部穿孔樣本中，識別正確的百分比，記為P：

(8)

成坑識別率代表了全部成坑樣本中，識別正確的百分比，記為H：

(9)

式中：n1為成坑樣本數;n2為穿孔樣本數;r1為識別成坑正確的樣本數;r2為識別穿孔正確的樣本數;n1+n2=n，n為總樣本數。

錯分率代表全部識別樣本中，未能正確識別的百分比，是損傷模式識別中的一個重要指標，主要考慮錯誤分類后的不同結果，記為Erate：

(10)

風險是基于最小風險準則的一個網絡指標，指靶板發生穿孔被誤識別為成坑損傷的百分比，記為R：

(11)

首先對網絡訓練輸入量進行自識別，表2為損傷識別算法對表 1中情況進行自識別驗證結果。

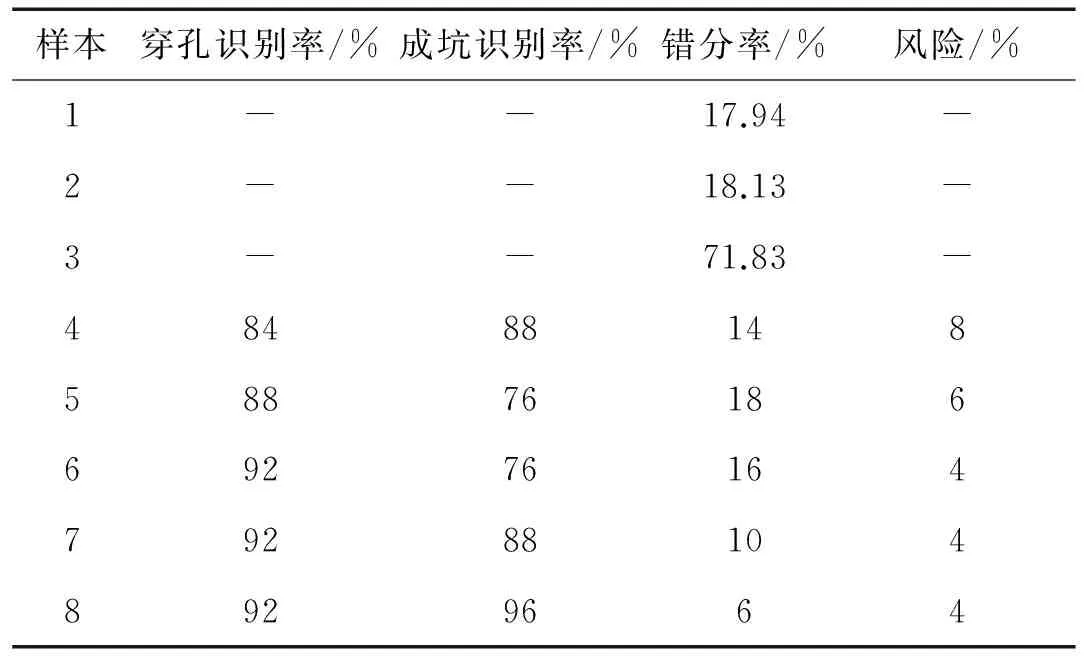
表2　訓練樣本損傷模式識別結果

由表2得到結論如下：

1) (0～62.5 kHz)部分的能量分數對錯分率的提升僅為0.19%，去掉(1 000～2 000 kHz)部分會大幅降低識別能力，為精簡網絡選擇2～6個能量比作為損傷識別的參數。僅采用能量分數時，識別能力較低，因此需要引入距離及時域參數。

2) 距離對總體自識別的提升是3.94%，因此距離因素是一個重要的損傷識別參數，驗證了前面關于距離的假設；

3) 時間參數中，上升時間和持續時間兩個參量之間相互影響，同時出現會降低總識別結果，其中上升時間對成坑自識別率提升12%，可以作為時間的損傷識別參數；

4) 加入截止頻率使成坑自識別率提升8%，因此可以作為一個損傷識別參數；

5) 損傷模式識別中選擇參數的最優組合為信號的上升時間、截止頻率、小波能量比的2～6個分量及傳播距離，此時各個識別結果均達到最優。

采用上述的損傷參數作為輸入量，對252個實驗樣本進行訓練，采用具有4個隱含層、每層10個節點的貝葉斯正則化的BP神經網絡，經過226次訓練后即達到設定的最小期望誤差值，圖10為網絡誤差曲線。

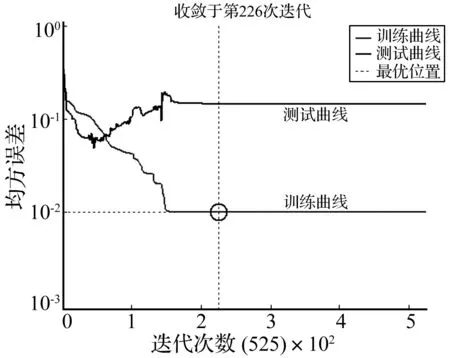
圖10　神經網絡訓練誤差曲線Fig.10 Curve of network training error

由圖10可知，發生穿孔損傷后，由于一部分動能被彈片帶走，導致超高速撞擊的能量不是隨動能單調變化的量，影響了算法對穿孔損傷的識別能力。因此在進行超高速撞擊損傷模式識別過程中，應注意適當調整訓練數據的比例，以達到預期的識別效果。

5結論

通過對大量超高速撞擊實驗數據進行研究，得到了一種基于BP神經網絡的鋁合金平板超高速撞擊損傷模式識別方法，通過該算法可以一定程度上實現鋁平板上的超高速撞擊損傷模式識別。通過對聲發射信號進行時域、頻域及小波分析，可得到與損傷相關的損傷參數，這些參數雖然不能直接表征損傷，但是與超高速撞擊過程中某些參量相關，可以提升識別算法的損傷模式識別能力。結合優選的貝葉斯正則化的BP人工神經網絡方法，可以有效地識別超高速撞擊的損傷模式，可以實現初步的識別功能，驗證了損傷參數的有效性。

[1] Upper Stage Explosion Places LEO Satellites at Risk[J]. Orbital Debris Quarterly News,2013, 17(1):1-2.

[2] Liou J C, Giovane F, Corsaro R, et al. LAD-C A large area debris collector on the ISS[C]//36th COSPAR Scientific Assembly. Beijing, China,2006.

[3] Prosser W H, Madaras E I. Distributed impact detector system (DIDS) health monitoring system evaluation[R]. Hampton: Langley Research Center, 2010．

[4] Spencer G, Sch?fer F, Tanaka M, et al. Design and initial calibration of micrometeoroid space debris detector (MDD)[C]//Proceedings of the 4th European Conference on Space Debris.Darmstadt, Germany,2005.

[5] 熊秋鵬. 基于神經網絡技術的空間碎片損傷模式識別研究[D]. 哈爾濱: 哈爾濱工業大學, 2012.

[6] Liu Wu-gang, Pang Bao-jun, Han Zeng-yao, et al.Acoustic emission detection and location for hypervelocity impacts based on wavelet transform[J]. Gaojishu Tongxin/Chinese High Technology Letters, 2009,19(2): 181-187．

[7] Liu Z D, Pang B J.A method based on acoustic emission for locating debris cloud impact[C]//Proceeding of the 4th International Conference on Experimental Mechanics,2009．

[8] 張凱, 龐寶君, 林敏. 碎片云撞擊聲發射信號能量特征小波包分析[J]. 振動與沖擊,2012, 31(12): 125-128．

ZHANG Kai, PANG Bao-jun, LIN Min. Wavelet packet analysis for acoustic emission signals caused by debris cloudimpact[J]. Journal of Vibration and Shock,2012,31(12): 125-128．

[9] Ditri J,Rose J L, Chen G. Mode selection guidelines for defect detection optimization using Lamb waves[C]//Proceeding of the 18th Annual Review of Progress in Quantitative NDE.Brunswick,ME,1991．

[10] Mackay D J C. Bayesian interpolation[J]. Neural Computation,1992, 4:415-447．

[11] Orre R, Lansner S, Bate A, et al. Bayesian neural networks with confidence estimations applied to data mining[J]. Computational Statistics & Data Analysis,2000,34(4):473-493．

[12] Wong M L, Lee S Y, Leung K W S. Data mining of Bayesian networks using cooperative coevolution[J]. Decision Support Systems, 2004(8):451-472.

Hypervelocity impact damage pattern recognition on aluminum plates based on Bayesian Regularization BP neural network

LIU Yuan, PANG Bao-jun

(School of Astronautics, Harbin Institute of Technology, Harbin 150080, China)

Damage patter recognition is a significant function module of on-board monitoring technology for space debris hypervelocity impact on spacecrafts. Based on hypervelocity impact acoustic emission on aluminum plates, hypervelocity impact acoustic emission signals were obtained through experiments. Combined with the accurate source location method for virtual wave front, specific time-frequency analysis and wavelet decomposition, the research extracted and optimized the relevant parameters of the damage pattern from the hypervelocity impact acoustic emission signals, thereby developing a Bayesian Regularization BP neural network for damage-pattern recognition and successfully recognizing the pit and hole damage patterns in an aluminum plate.

space debris; hypervelocity impact; acoustic emission; neural network; damage pattern recognition

10.13465/j.cnki.jvs.2016.12.004

國家“十二五”空間碎片專項

2015-05-18修改稿收到日期：2015-07-02

劉源 男，碩士，1987年5月生

龐寶君 男，博士，教授，博士生導師，1963年3月生

V414.3；TB559

A