基于R-W方法的多自由度的運動特性研究及應用

梁 夏，吳曉光，張 弛

（武漢紡織大學 機械與自動化學院，湖北 武漢 430200）

基于R-W方法的多自由度的運動特性研究及應用

梁 夏，吳曉光*，張 弛

（武漢紡織大學 機械與自動化學院，湖北 武漢 430200）

基于羅伯森和威藤堡提出的R-W方法，針對一種新型全自動鞋套機的驅動系統，開展了多剛體動力學R-W方法的探討。提出研究鞋套機的驅動系統的基本建模思路，建立了鞋套機的驅動系統的多剛體動力學模型及運動方程，論證R-W方法對特殊機械可行性；通過ADAMS軟件對已建立的鞋套機驅動系統進行動力學仿真，其數學模型與虛擬仿真結果基本一致；通過部分數值分析和仿真分析，為設計新型無紡布專用鞋套機結構設計、關鍵驅動零部件優化設計提供可靠的分析依據。

無紡布鞋套機；R-W方法；多剛體運動；仿真

為解決塑料鞋套易產生靜電以及對環境的污染等問題，利用無紡布易分解，可循環再利用等特點，設計了一款全自動無紡布鞋套機。然而鞋套機驅動系統影響到整個系統的工序轉換的穩定性和生產的效率，對其分析研究十分重要。鞋套機驅動系統為復雜的空間結構，運用經典力學方法研究其運動規律已經很難解決驅動系統中多個零部件相互作用。羅伯森和威藤堡提出的R-W方法為其提供了強大的理論武器，它是以多個相互作用的剛體組成的復雜系統為研究對象，結合計算機技術，對其進行運動學和動力學分析。本文將采用多剛體系統動力學中提出的R-W方法來建立鞋套機驅動系統的數學模型，并結合ADAMS綜合對其進行動力學仿真分析，以獲得最佳的數據。

1　鞋套機驅動系統多剛體模型建立

1.1 全自動無紡布鞋套機系統的描述

全自動無紡布鞋套機的模型主要有進料裝置、對折裝置、中心驅動裝置、夾具、出料裝置、機架和包縫機等組成。原料上采用了無紡布解決了塑料鞋套彈性問題和白色污染；技術上采用全自動縫合技術提高了生產率，減輕了勞動強度。中心驅動裝置是全自動鞋套機驅動系統研究的重點，是整個鞋套機的重要組成部分，在工作過程中，電機帶動中心旋盤繞橢圓形軌道做圓周運動，完成無紡布原料到鞋套成品的工序。鞋套機驅動系統結構圖如圖1所示。

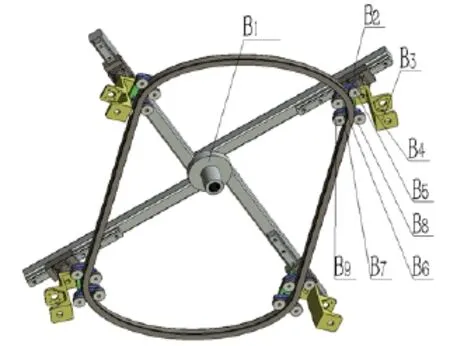
圖1　鞋套機驅動系統結構圖

1.2 模型的建立及運動方程

全自動無紡布鞋套機驅動系統為9個剛體相互約束連接的模型。根據圖1鞋套機驅動系統結構圖內分體的聯接和相對運動，確定鞋套機驅動系統的拓撲構型。按照多剛體動力學中R-W的理論，B0表示鞋套機機架，B1表示旋轉十字架，B2表示直線滑塊，B3表示支撐架，B4、B7表示鞋套機機身導輪支撐，B5、B6、B8、B9表示導輪。將連接相連剛體的有向線段記做鉸hj(j=1,2…,9)，其中h2為移動副，其他鉸為轉動副。選用R-W圖論方法，得到如圖2所示的鞋套機驅動系統有向圖。為了能獲得其樹形系統的運動學方程，簡化鞋套機驅動系統的非樹形結構為樹形結構。分割掉鞋套機驅動系統有向圖中鉸h11、h12、h13和h14，獲得如圖3所示的鞋套機樹形系統圖。

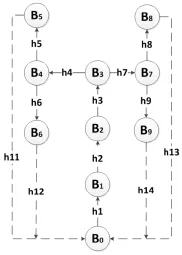
圖2　鞋套機驅動系統有向圖

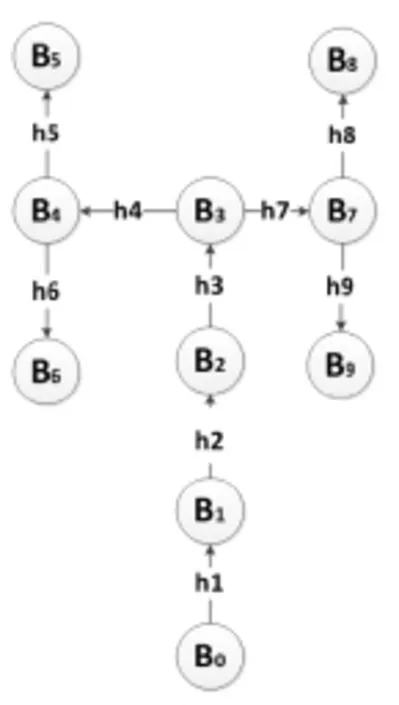
圖3　鞋套機樹形系統圖

依據R-W理論確定各剛體連體基，設機架的連體基為（O0,e0）。設各剛體的內接鉸為hj(j=1,2…,9)且其中h2（滑移鉸）、hj(j=4,5,6,7,8,9)均與質心重合，且均為單自由度轉動鉸，則派生樹共有9個自由度。

則可得鞋套機驅動系統的關聯矩陣S和通路矩陣T為：

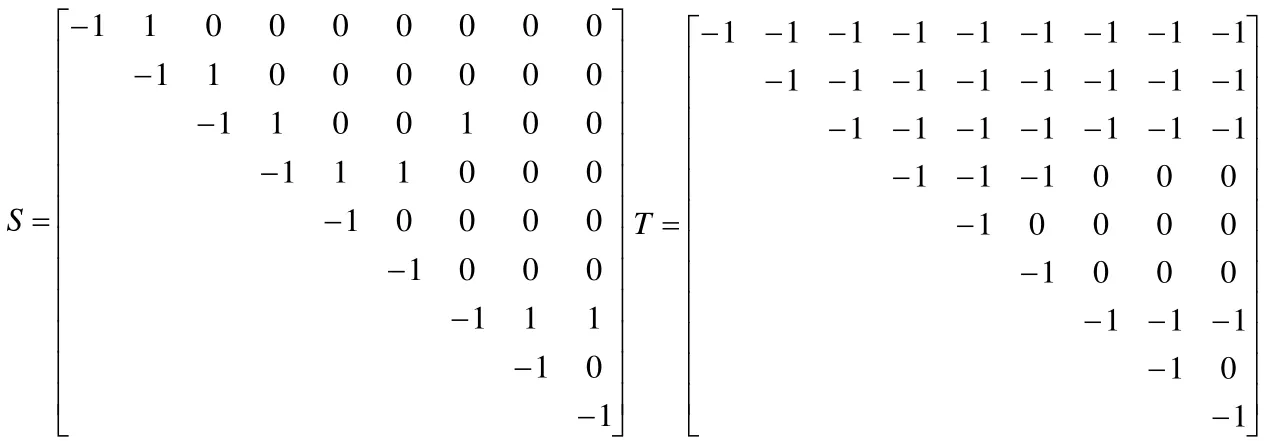
設機架B0和中心旋轉盤B1的連體基（Oi,ei）(i=0,1)重合，為垂直軸,并且相等。B2的質心O2在軸上，z2為h2鉸的滑移距離，規定內接鉸hi指向質心Oic的距離為iρ，內接鉸hi指向外接鉸hi+的距離為Lij(j=1,2,3為連體基軸的方向)。

則通路矢量為：

即可得通路矢量dij構成的矩陣為：

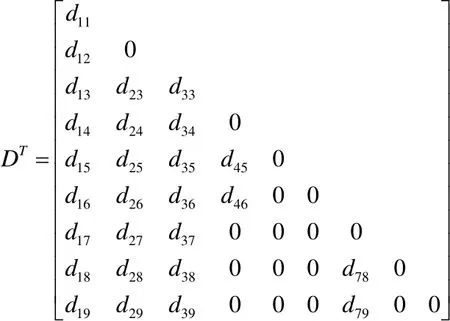
綜上可得鞋套機樹形系統中各剛體質心構成的運動方程[2]為：式中[r]——由Bi剛體質心位置ir矢徑構成的矩陣；

r0——剛體B0質心矢徑；

[1]n——元素為1的nx1維列陣；

[D]——為通路向量dij構成的nxn矩陣。

1.3 約束方程

鞋套機驅動系統以中心旋盤為主剛體，其余為附件的旋轉運動。ρ是以軌道中心為原點，α為橢圓長半軸，b為橢圓短半軸的極坐標參數方程，滾輪沿著這個軌道做圓周運動[3]。軌道簡圖如圖4所示。

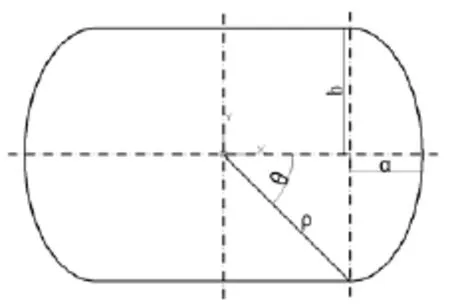
圖4　軌道簡圖

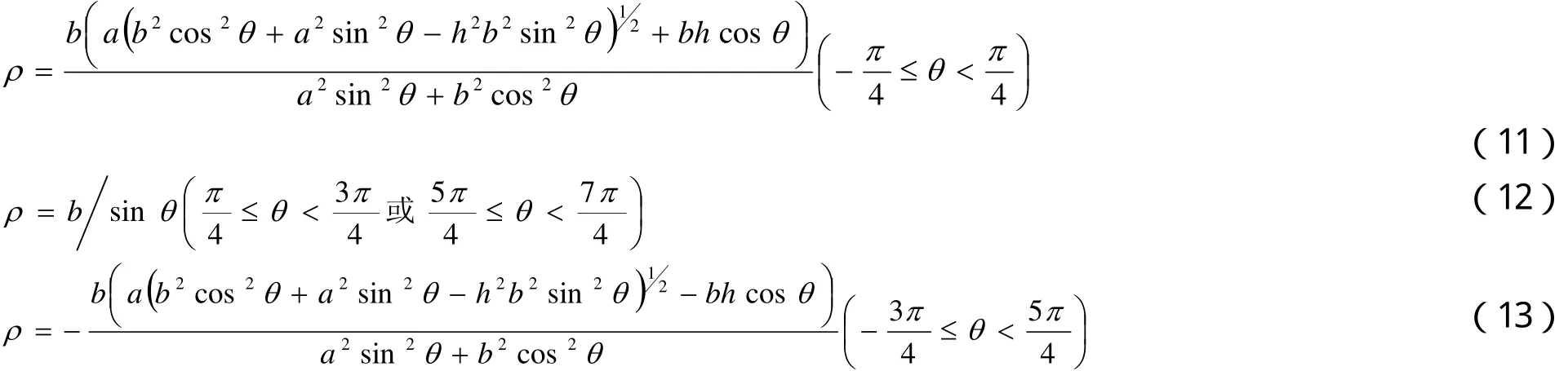
2　模型仿真分析

2.1 MATLAB的仿真分析

根據以上內容列出的鞋套機驅動系統各剛體數學模型，在MATLAB中編寫程序進行仿真研究[4-5]，其中鞋套機驅動系統數學模型的相關參數，如質心到鉸點的向量，各剛體的尺寸等運用SolidWorks估算和測量，中心旋盤以30°/s旋轉得到滑塊的響應曲線如圖5所示。

圖5　MATLAB中計算的位移、速度曲線

2.2 基于ADAMS的仿真分析

在Adams中，鞋套機驅動系統虛擬樣機如圖6所示。為了獲得鞋套機驅動系統虛擬仿真研究與實際工作狀態一致的結果，需要對導入的每個零部件的相關屬性進行編輯，如材料、質量、轉動慣量等。再設置各個零件的運動關系，完成各運動部件之間的連接副和驅動，對專用鞋套機進行運動學及動力學仿真。其中運算和求解的各參量矩陣是根據力學模型獲得的，然后建立了系統相關數學模型。最后選取專門的多剛體系統動力學數值分析算法迭代求解，并分析其結果[6]。

圖6　專用鞋套機驅動系統虛擬樣機

圖7　滑塊位移響應曲線

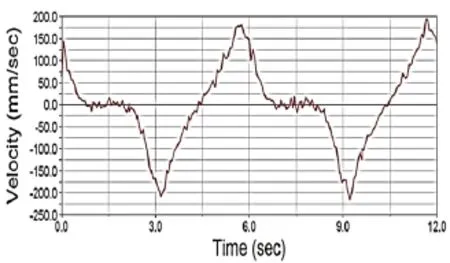
圖8　滑塊速度響應曲線圖

圖9　加速度響應曲線

從圖5、圖7和圖8可以看出，基于MATLAB和ADMAS對鞋套機的仿真結果基本吻合，證實了所建立模型的有效性。滑塊的位移大約-175～50mm變化，是從軌道直線與半橢圓相切處開始運動，滿足半橢圓-直線-半橢圓-直線的運動規律。從圖8可以看出滑塊的速度曲線趨勢基本與圖5一致，但出現微小的波動，這是由于沿著軌道運動的兩滾輪中心距比軌道寬0.5mm，受力狀態不均勻引起的。圖9為滑塊的加速度響應曲線，可以看出，啟動瞬間加速度比較大，在一定范圍波動。

3　結論

本文應用多剛體動力學中的R-W理論，以鉸的相對坐標為獨立變量，對鞋套機驅動系統進行抽象與簡化，建立與實際機械系統一致的數學模型，對鞋套機驅動系統進行空間運動學數值分析，研究鞋套機驅動系統的運動規律。再結合數字化虛擬樣機開發工具ADAMS對專用鞋套機進行動力學分析，得到各個零件的位移、速度、加速度等運動規律，有效的研究了系統動態特性。同時，通過對比證實了R-W方法研究特殊機械的可行性。全自動無紡布鞋套機的研究目前在國內尚首空白，文中的理論研究與產品研究將為此款機型實用化奠定基礎，為正在研究類似工作的工程技術人員提供參考。

[1] 劉延柱，潘振寬，戈新生，多體系統動力學[M]. 北京：高等教育出版社，2014.

[2] 寧介雄，鐘志強，張建軍，等．多剛體學R-W方法對雙搖臂機構的優化[J]．建筑機械化，2010，4（11）：42-45.

[3] 王鵬程，方勇純，相吉磊，等．回轉旋臂式船用起重機的動力學分析和建模[J]．機械工程學報，2011，47（20）：34-40.

[4] 齊朝暉．多體系統動力學[M]．北京：科學出版社，2008.

[5] 韓清凱，羅忠．機械系統多體動力學分析、控制與仿真[M]．北京：科學出版社，2010.

[6] 陳力平，張云清，任衛群，等．機械系統動力學分析及ADAMS應用教程[M]．北京：清華大學出版社，2005.

Research and Application of Multi-degree of Freedom Motion Characteristics Based on R-W Method

LIANG Xia, WU Xiao-guang, ZHANG Chi
(School of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan Hubei 430200, China)

This paper has proposed a basic modeling in studying the driving system of this shoe-cover machine, built the multi rigid-body dynamical model and motion equations of this system, and proved the effectiveness and feasibility of R-W method to the special machine. Through ADAMS software, the dynamic simulation of this established driving system has been analyzed, and the outcomes are basically consistent with that of its mathematical model. Through numerically analyzing and simulation analysis, this paper can provide reliably analytic references for the design of structure of a new type special non-woven fabric shoe cover machine and the optimized design of key driving components and parts.

shoe cover machine; R-W method; multi rigid body motion; simulation

TU311.3

A

2095－414X(2016)03－0048－04

吳曉光（1954-），男，教授，研究方向：數字化紡織裝配及關鍵技術.